电力有源滤波器中谐波电流检测与仿真*

高海洲，叶天凤

(湖北理工学院电气与电子信息工程学院，湖北黄石435003)

近年来，电力电子装置的应用日益广泛，各种电力电子装置成为主要的谐波源，谐波带来一系列的问题［4］，也加剧了对电网的污染。相对传统的LC滤波器，电力有源滤波器不仅能对频率和幅值都变化的谐波进行动态跟踪补偿，且补偿特性不受电网阻抗的影响，因而受到广泛的重视和应用。电力有源滤波器的基本思想六七十年代即已形成。八十年代以来，由于自关断电力电子器件的成熟、PWM技术的进步和瞬时无功功率理论的提出，电力有源滤波器在谐波补偿中的研究及应用也逐渐深入［3］。国内外目前研究较多的是电压型并联电力有源滤波器，本文将就该类型滤波器设计中的谐波电流检测加以阐述。

1 谐波电流检测补偿原理［2］

有源滤波器是由一组开关器件和无源储能元件如电感和电容组成，其系统主要由指令电流运算电路和补偿电流发生电路两大部分组成。并联型电力有源滤波器如图1所示，首先检测补偿对象的电流(或电压)，经过指令运算电路得到补偿电流的指令信号，然后对变换器中的开关器件进行实时的通断控制，使变换器向电网输出与负载的谐波电流ih大小相等的补偿电流ic，此时电网电流is=iL－ic=iL1+ihic=iL1，于是电力系统中只流过基波电流iL1(包括基波有功电流iL1P和无功电流iL1Q)。如果进一步使ic=(ih+iL1Q)，则此时电网电流is=iL1P，即电力系统中只流过有功电流iL1P，这样既将电源侧电流补偿为正弦波，又进行了无功补偿。

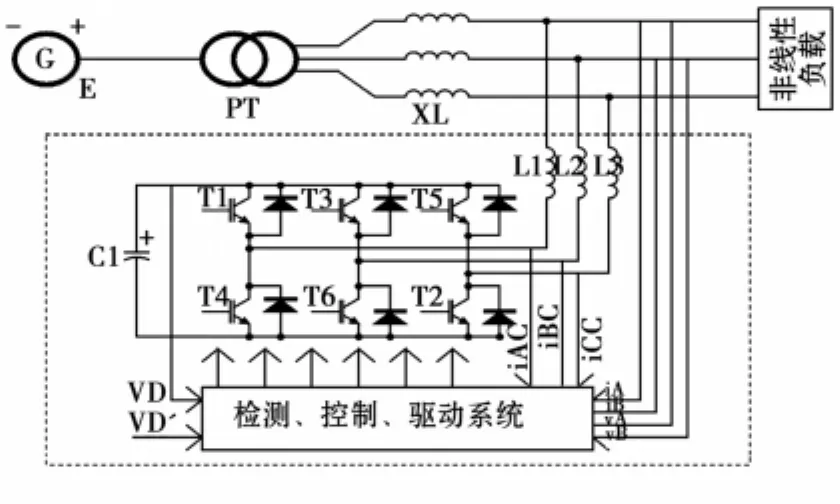
图1 并联有源滤波装置原理电路

当有源滤波器同时用于补偿谐波和无功时，就需要实时检测出负载中的谐波电流和无功电流。图1中负载电压vA、vB、vC以及三相电流的瞬时值iA、iB、iC都是可以检测的，运用id、iq法从iA、iB、iC中适时准确地分离出谐波电流ih和无功电流iL1Q，再以(ih+iL1Q)做为补偿电流的指令信号，使图1主电路输出补偿电流ic，完全补偿负载谐波电流和无功电流。

设三相三线制电路中，各相电压、电流的瞬时值分别为vA、vB、vC，iA、iB、iC，则其三相有功瞬时功率 P3的表达式为:

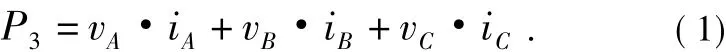
如图2所示，如果把它们变换到两相正交静止的α—β坐标系，将两相坐标系的α轴取在A相轴线上，β轴超前α轴90，则两相系统中的有功功率为:

图2 矢量图

在此坐标系中，如果对三相电压、电流做如下变换:

C23=，式中为 C23的逆阵。

将式(3)、式(4)中的 vα、vβ、iα、iβ代入(1)式，化简后得:

因此，将三相互差120°(2π/3)的 A、B、C 静止坐标系统用两相正交的α—β静止坐标系统代替后，按(3)、(4)、(5)、(6)式进行电流、电压变换，则α—β系统中的功率等于三相A、B、C系统中的功率。

如图3所示，如果把它们变换到两相正交旋转的d—q坐标系，取d轴与矢量V·重合，d轴超前q轴90°。在d—q两相旋转坐标系中，电流在d轴上的投影分量id和iq分别是有功电流和无功电流，由图3可得:

在两相旋转的d—q坐标系中，有功功率P和无功功率Q分别为:

因此可得出结论，经过上述各坐标变换后，d、q系统，α、β系统的功率都与三相A、B、C系统的功率相等。

由分析知，如果 iA、iB、iC是基波正弦，则 iα、iβ也是基波正弦，这时对应的 id、iq是直流量 Icosφ、Isinφ。如果 iA、iB、iC是高频n次谐波电流，例如:

由(9)式可得:

图3给出了一种三相 A、B、C 谐波电流 iAh、iBh、iCh的实时检测电路。电网电压相位信号由一个软件锁相环和正、余弦发生电路得到。变换后得到的电流id、iq中将含有与基波电流iL1对应的直流分量Id、Iq，还含有对应于n次谐波电流ih相的(n－1)次谐波电流，id、iq经低通滤波器LPF滤波后，得到无衰减的直流分量，其中的(n－1)高次谐波分量被滤除，将LPF输出的只与负载基波电流iL1相对应的电流Id、Iq，按式(9)做逆变换后，即可得到基波电流iA1、iB1和iC1。

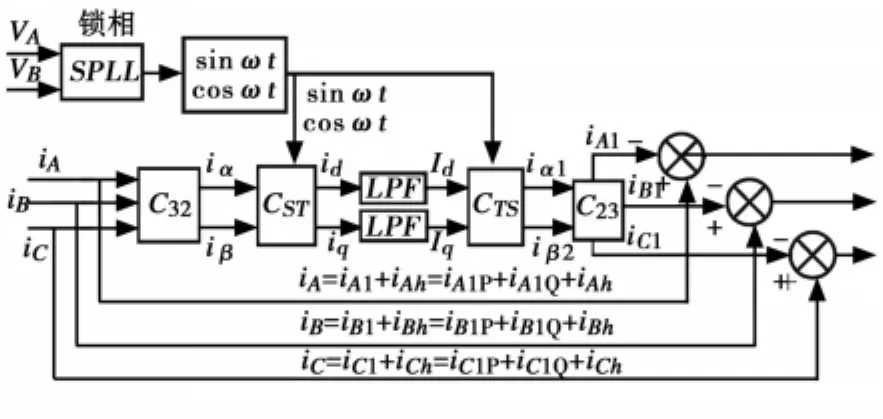
图3 谐波电流及无功电流检测电路

将检测到的实际电流iA、iB、iC与以上计算得到的基波电流 iA1、iB1、iC1相减，即可得到三相谐波电流 iAh、iBh、iCh，以此作为三相变换器输出补偿电流的指令信号。

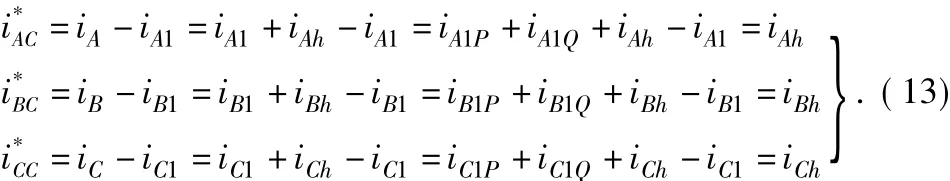
如果需要同时补偿负载电流中的谐波电流ih和基波无功电流i1Q，则可在图3中断开电流iq的通道，使送入低通滤波器 LPF 中的 iq=0，这是经 CTS变换后输出的 iα1、iβ1中将只有有功电流分量而无无功电流分量，使C23的输出仅是基波有功电流iA1=iA1P、iB1=iB1P、iC1=iC1P，它们与负载电流 iA、iB、iC相减后得到的将是谐波电流与基波无功电流之和，以此作为图1中电力有源滤波器输出的补偿电流指令值i*c=(ih+iL1Q)。

2 仿真分析［1］

基于MATLAB/SIMULINK对上述原理进行了仿真。仿真时用一个带容性负载的不控整流桥作为非线性负载。仿真结果如图4和图5所示，图4为A相负载电流和谐波电流的波形，图5为A相负载电流和基波电流的波形。

图4 A相负载电流和谐波电流

图5 A相负载电流和基波电流

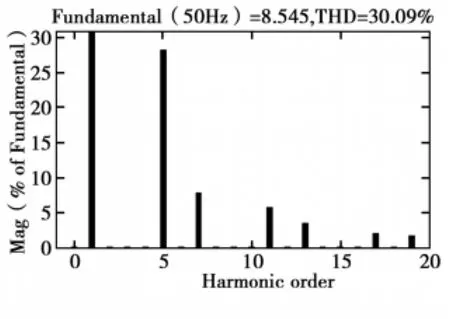
图6 负载电流频谱分析

图7 基波电流频谱分析

由频谱分析可以看出，应用图3所示的谐波电流及无功电流检测电路可以得到很理想的基波电流，它和负载电流相减，就可以得到谐波电流值。负载电流的谐波主要是5、7、11、13 次谐波［2］。

3 结束语

基于瞬时无功理论，将三相坐标系下的电流变换到d—q坐标系下，使三相坐标系下的谐波电流在d、q轴下对应为直流分量上叠加的高频分量，通过低通滤波器可分离出谐波电流及无功电流，从而得到电力有源滤波器输出的补偿电流指令值，利用PI调节器或电流滞环可实现补偿谐波指令的跟踪。利用DFT算法或数字滤波器也可从总谐波中分离出各次谐波并进行独立补偿。

［1］刘进军，刘波，王兆安.基于瞬时无功功率理论的串联混合型单相电力有源滤波器［J］.中国电机工程学报，1997，17(1):3741.

［2］陈坚.电力电子学［M］.北京:高等教育出版社，2002.

［3］王兆安，李民，卓放.三相电路瞬时无功功率理论的研究［J］.电工技术学报，1992，7(3):55 －59.

［4］王兆安，杨君，刘进军.谐波抑制与无功补偿［M］.北京:机械工业出版社，1998.

［5］AkagiHirofumi.New Trends in Active Filters For Power Conditioning［J］.IEEE Trans on Industrial Applications，1996，32(6):1312.