弱耗散Novikov方程强解的整体存在性和衰减性

胡巧怡



弱耗散Novikov方程强解的整体存在性和衰减性

胡巧怡

（华南农业大学 数学系，广东 广州 510642）

研究弱了耗散Novikov方程的Cauchy问题，得到强解的整体存在性和衰减性.

Novikov方程；弱耗散；整体存在性；解的衰减

最近Novikov[1]导出了一个带三次方非线性项的可积方程

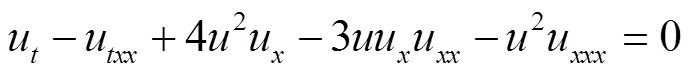
该方程具有许多与Camassa-Holm方程形似的性质，如同样具有尖峰解、双Hamilton结构结构等.

在许多实际情况下，人们不能忽视能量的耗散.Ott等[6]曾经研究了能量耗散对KdV方程解的影响（包括对行波解的影响大小）；Chidaglia[7]把弱耗散KdV方程作为有限维动力系统模型，研究了该方程解的长时间性态；吴书印等研究了周期[6]和非周期[9]的弱耗散Camassa-Holm方程强解的爆破、爆破率、整体存在性和衰减性；胡巧怡等[10]研究了周期的弱耗散杆方程解的爆破性质.

受此启发，我们考研究下面非周期的弱耗散Novikov方程强解的整体存在性和衰减性.

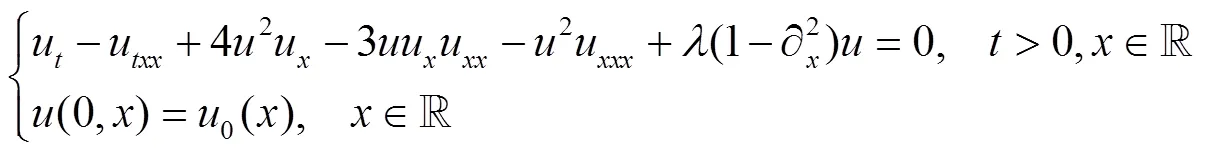
1 预备引理

或

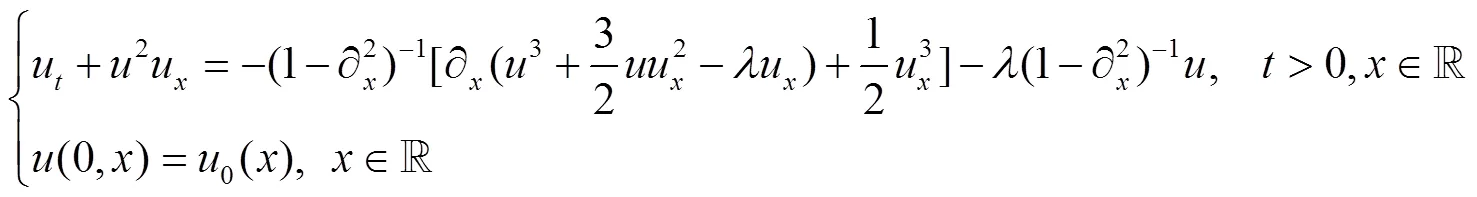
类似文献[4]的方法，可得弱耗散方程（3）的局部适定性.

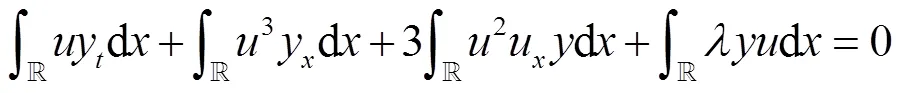
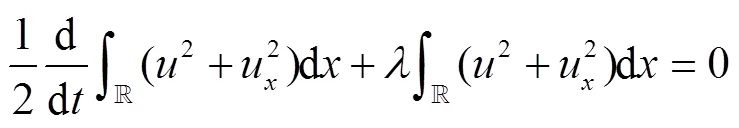
引理得证.

由引理1结合Sobolev不等式，得推论1.

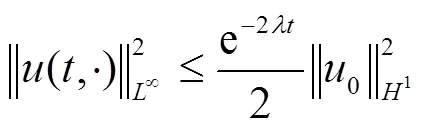
证明 由引理1，得

结合Sobolev不等式，得

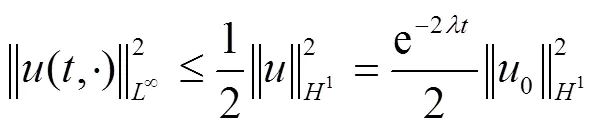
推论证毕.

类似文献[4]中的方法，可得如下爆破机制.

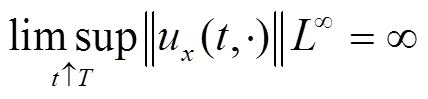
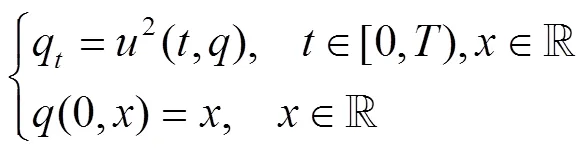
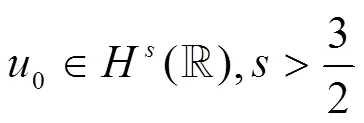
证明 由式（5）得

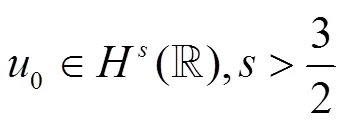
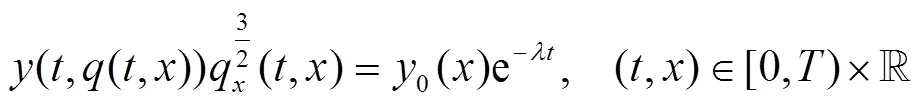
由方程（3），得

引理证毕.

2 解的整体存在性和衰减性

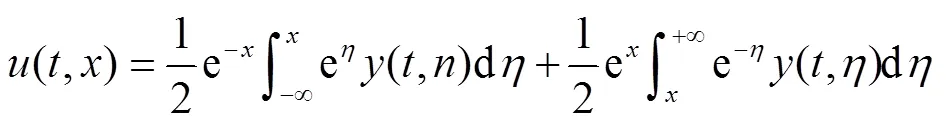
由此推出

由推论1得

将式（9）和式（10）相加，得

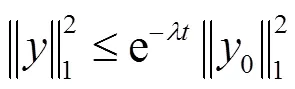
注：1）Novikov方程的整体强解没有衰减性，定理2说明了弱耗散Novikov方程与非耗散Novikov方程在长时间性态有明显的不同，即弱耗散项对Novikov方程整体强解的长时间性态有很大影响.

[1] NOVIKOV V S. Generalizations of the Camassa-Holm equation[J]. J Phys A: Math Theor, 2009: 42: 1-14

[2] TIGLAY F. The periodic Cauchy problem for Novikov's equation[J]. Int Math Res Not, 2010: 267: 1-16.

[3] NI Lidiao, ZHOU Yong. Well-posedness and persistence properties for the Novikov equation[J]. J Differential Equations, 2011, 250: 3002-3021.

[4] WU Xinglong, YIN Zhaoyang. Well-posedness and global existence for the Novikov equation[J]. Ann Sc Norm Sup Pisa, (sumitted).

[5] WU Xinglong, YIN Zhaoyang. Global weak solutions for the Novikov equation[J]. Y Phys A: Math Theor, 2011, 44: 055202 1-17.

[6] OTT E, SUDAN R N. Damping of solitary waves[J]. Phys Fluids, 1970, 13: 1432-1434.

[7]GHIDAGLIA J M. Weakly damped forced Korteweg-de Vries equations behave as a finite dimensional dynamical system in the long time[J]. J Differential Equations, 1988, 74: 369-390.

[8] WU Shuyin, YIN Zhaoyang. Global existence and blow-up phenomena the weakly dissipative for Camassa- Holm equation[J]. J Differential Equations[J]. 2009, 246: 4309-4321.

[9] WU Shuyin, YIN Zhaoyang. Blow-up and decay of the solution of the weakly dis-sipative Degasperis-Procesi equation[J]. SIAM J Math Anal, 2008, 40: 475-490.

[10] HU Qiaoyi, YIN Zhaoyang. Blowup and blowup rate of solutions to a weakly dissipative periodic rod equation[J]. J Math Phys, 2009, 50(8): 1-16.

Global Existence and Attenuation of the Strong Solution of Weak Dissipative Novikov Equations

HUQiao-yi

(Department of Mathematics, South China Agricultural University, Guangzhou 510642, China)

The paper studies weak dissipative Novikov equations’ Cauchy problems and obtains the global existence and the attenuation properties of their strong solutions.

Novikov equations; weak dissipation; global existence; attenuation of solutions

1006-7302（2012）01-0020-05

O175.29

A

2011-09-05

广东省自然科学基金资助项目（S2011040001127）；广东省教育厅育苗工程项目（LYM11030）

胡巧怡（1979—），女，广东惠州人，讲师，博士，从事非线性偏微分方程研究.