模糊推理方法在无人机编队目标分配中的应用*

周小程,严建钢,马响铃

(海军航空工程学院,山东 烟台 264001)

在无人机编队作战过程中,针对不同目标的特性,作战任务也要多方面考虑,而考虑的方面越多,就越难取舍和判断,尤其是实际过程中有很多定性的目标[1]。目前针对多目标的目标分配问题的解决途径一般有层次分析法[2-3],线性加权法以及灰色理论等[4-6]。上述理论在实际中或多或少地存在着一些问题且不能很好地解决定性条件下目标的分配问题。

本文针对不同目标在定性条件下的量化评估方法,考虑了不同定性条件的相对隶属度,采用更为全面的信息,建立基于模糊推理的无人机编队作战中目标分配方法的数学模型,对该模型进行了求解分析,并应用算例对该模型的有效性和可行性进行了证明。

1 模型的描述

设在无人机编队中有n架无人机,用｛u1u2… un｝表示,需要对n个不同目标进行攻击,用表示,对于这n个不同目标分配需要考虑m个不同的定性条件,设在第k个定性条件下,第i架无人机对第j个目标的优属度为,此处的优属度可以通过定性目标的量化模型得到,这样,对每一个目标我们都可以得到一个关于无人机和目标之间的优选决策矩阵Q,应用优化算法将不同权重的目标优选决策模型转化为特征值矩阵P,并进行求解即可以得到无人机编队针对不同定性条件的最佳配置方案。

2 对定性条件优选决策矩阵的求解

比较不同无人机ui,在定性条件k下,关于某个目标t的优越性,首先对编队中任意两架无人机进行比较,从而得到比较度eij,若ui比uj优越则记eij为1,ui和uj同样优越eij记为 0.5,ui比uj不优越eij记为0。从而得到如下所示比较矩阵:

对矩阵中的第i行求和:

可以得到在定性条件k下,无人机ui关于某个目标t的优越性,此时就可以得到一组数据｛E1E2… En｝,对这组数据进行排序,可以简单反映出无人机ui的优越性,选择最大的Emax作为基准,并进行比较,即令

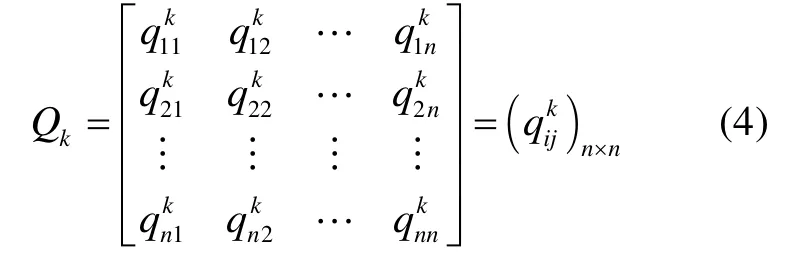
其中,i ＝ 1,2,… ,n; j ＝ 1,2,… ,n; k ＝1,2,… , m 。

3 无人机编队目标分配的优化模型

由于不同目标定性因素的重要程度不同,所以这里可以引入重要度向量的概念,可以根据具体的实际情况和专家经验给出重要度向量的值,重要度向量的基本形式可以表示为

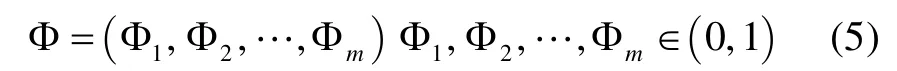
同时,为了整合和评估上述重要度的值,引入不同定性因素的相对隶属度,可以表示为

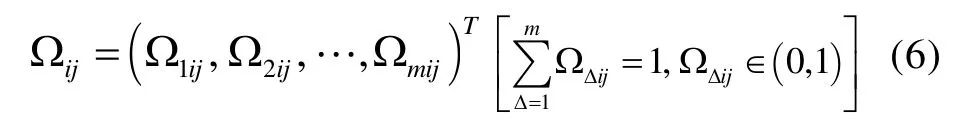
实际情况中,针对不同的定性条件,其权重也是不同的,可以表示为

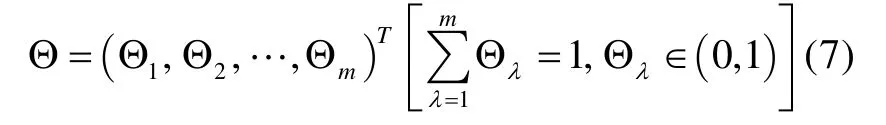
根据模糊理论和上述的分析,最佳的相对隶属度可以通过最小化欧式加权距离求出,可以表示如下:

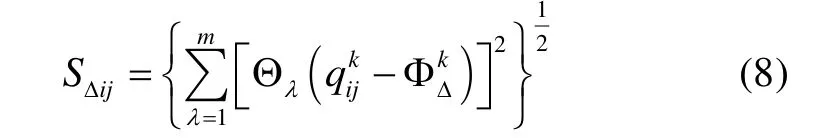
为了求解相对隶属度Ωij,构造下列模糊目标函数[7-8]:

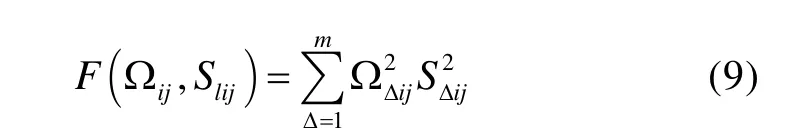
应用最小二乘法[9-11]求满足下列目标函数的Ωij,即

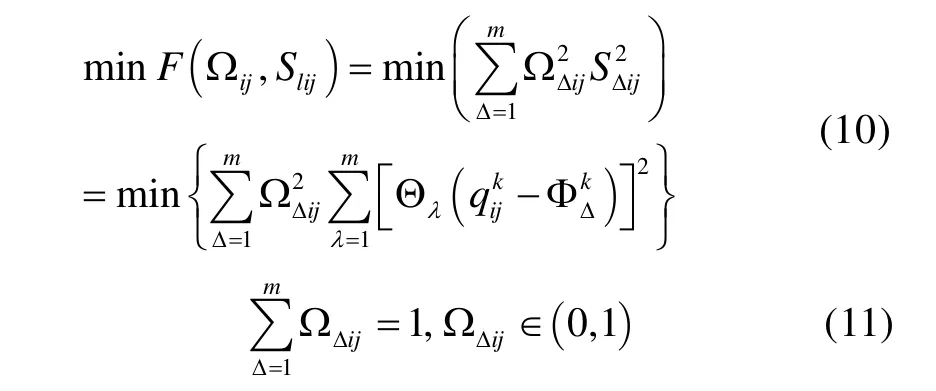
最后解出:

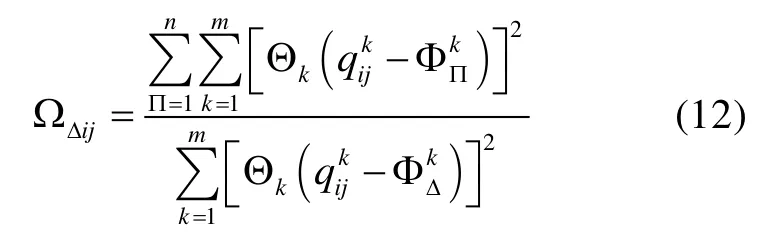
由上式可以得到每个重要度的相对隶属度值,则可以更全面反映每个定性因素的特性。为了更全面地判断全部信息,下面给出了综合特性表达式:

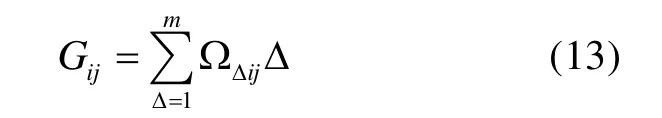
其中,Gij为重要度变量的特征值,由此可以得到重要度变量的特征值矩阵。

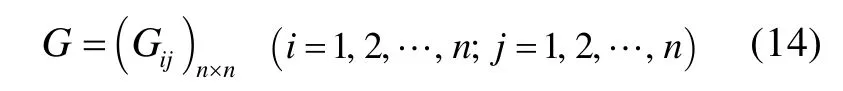
根据上述分析,给出无人机目标分配的优化模型,即

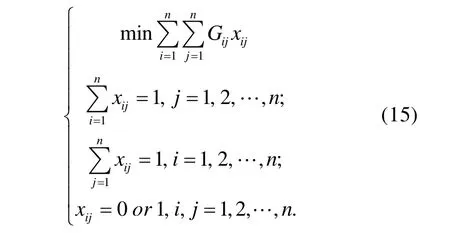
4 实例计算

无人机编队有4架无人机,要对4个不同目标进行攻击,在满足作战能力和任务要求的基础上,对于攻击目标另有3个定性条件,即实施攻击前目标对无人机的威胁程度,实施攻击后目标的毁伤程度,无人机本身的可靠性。

首先,比较4架不同类型无人机在3个定性条件下,关于 4个目标的优越性。以第 1个定性条件下,关于4个目标的优越性排序为例进行说明。首先给出比较矩阵结果:

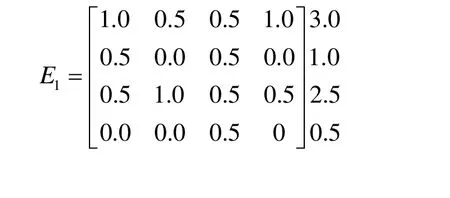
从而得到优选决策矩阵:

按照上面的方法得到第 2、3个定性条件下,关于4个目标的优越性排序为例进行说明。优化决策矩阵 Q2,Q3,如下:

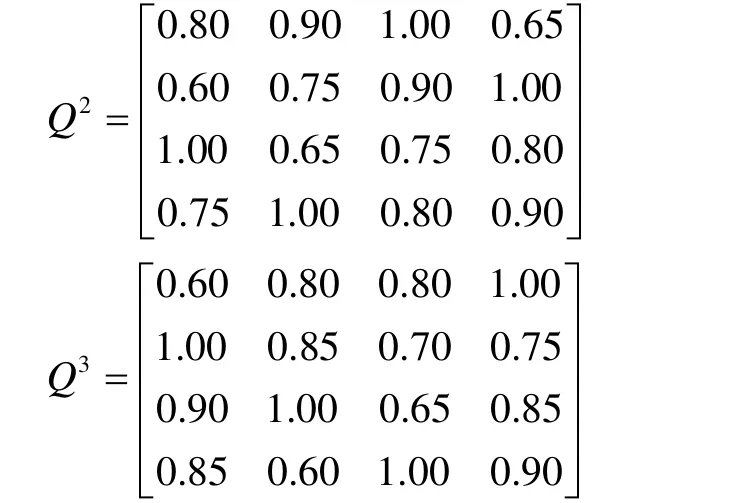
将上述特征值矩阵优化无人机目标分配的优化模型,可以得到最优解:

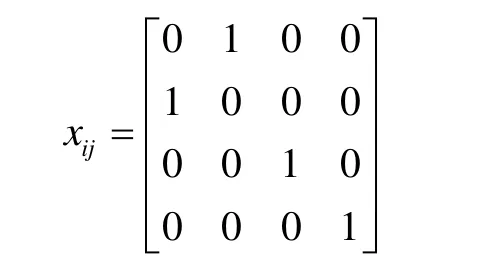
从上式中可以得到最终的结果,即第1架无人机负责对目标2进行攻击,第2架无人机负责对第1个目标进行攻击,第3架无人机负责对第3个目标进行攻击,第4架无人机负责对第4个目标进行攻击,上述方案即为无人机编队在3种定性条件下实施目标攻击任务的最佳配置方案。

5 结束语

在实际的无人机作战任务中,定性的条件是大量存在的。因此,本文在对定性条件优选决策矩阵进行求解的基础上,基于模糊推理的理论建立了在定性条件下无人机编队目标分配的优化模型,建立的模型较全面地反映了无人机作战过程中定性条件下的目标分配信息,为制定攻击决策提供了一种公正客观的方法,对于解决定性条件下的目标分配十分有效,具有较好的应用价值。

本文在建立无人机编队目标分配模型时未考虑定量条件的约束,下一步的研究重点是如何应用模糊推理的相关理论建立在定性和定量两种条件下的目标分配优化模型。

[1]许智辉,李执力. 无人机武器化趋势及其对未来战争的影响[J].飞航导弹,2004(6):44-46.

[2]杨州,袁卫卫,王明利. 基于改进层次分析法的对地攻击方案优选决策[J].火力与指挥控制,2011(1):111-113..

[3]贾跃,宋保维,赵向涛. 基于层次分析法的占领阵位方案优选评判方法[J].火力与指挥控制,2006(7):24-25.

[4]罗来科,陈军. 基于灰色理论的导弹部队机动方案优选模型研究[J].科学研究,2008(11):5-7.

[5]熊伟,张晶炜,何友. 基于多维分配和灰色理论的航迹关联算法[J].电子与信息学报,2010(4):898-901.

[6]衣晓,关欣,何友. 分布式多目标跟踪系统的灰色航迹关联模型[J].信号处理,2005(6):653-655.

[7]刘海峰,刘付显,王君. 基于模糊综合函数的目标属性识别模型[J].模糊系统与数学,2005(1):156-157.

[8]Li R J, Lee E S. Denovo programming with fuzzy coefficients and multiple fuzzy goals[J].Math Analysis and Appl,1993,72:212-220.

[9]Lee E S, Li.R.J.Fuzzy multiple objective programming and compromise programming with pateto optimum[J].Fuzzy Sets and System.1993(53):275-288.

[10]Philippe Lemmerling, Nicola Mastronardi. Subine Van Huffel fast algorithm for solving the Hankel/Toeplitz structured total least squares problem[J]. Numerical Algorithms,2000(23):371-392.

[11]Golub G H,Van Loan C F.An analysis of the total least squares problem[J].SIAM J Number Anal, 1980(17):883-893.