多晶拉伸试样表面各晶粒滑移带研究

石艳柯，张庆华，张克实

(1.华北水利水电学院，河南郑州 450011;2.广西大学，广西南宁 530004)

多晶拉伸试样表面各晶粒滑移带研究

石艳柯1，张庆华1，张克实2

(1.华北水利水电学院，河南郑州 450011;2.广西大学，广西南宁 530004)

采用建立在晶体塑性理论基础上的晶体塑性有限变形计算方法，针对多晶铜试样单轴拉伸过程中晶体滑移造成试样的滑移痕迹进行了数值研究，并对拉伸过程中材料内部的应力、应变的不均匀分布进行了初步统计分析.利用三维有限元模拟多晶铜试样的拉伸变形，通过晶体塑性滑移面与试样观察面交线的几何分析，得到了不同滑移系启动造成的多晶试样观察面滑移痕迹.所得结果表明，将建立在连续滑移描述基础上的晶体塑性理论运用于数值模拟，能够较合理地呈现多晶试样拉伸的表面滑移带痕迹，能够考虑材料内部结构不均匀而引起的宏观响应.

晶体塑性理论;滑移带痕迹;不均匀;数值模拟

尽管人们已建立了数学上看似完备、针对连续均匀材料的经典塑性理论体系，但是经典塑性理论因不考虑金属材料实际存在的复杂微结构及其微结构变形机制对材料塑性变形规律的影响，因此难以对金属材料在复杂加载条件下的塑性行为进行合理的表述.材料学的研究证实了金属塑性变形的主要机制是大量位错运动造成的原子密排面滑移.晶体塑性理论考虑了金属材料的晶格结构和晶粒尺度下的变形机制，因此人们期望利用晶体塑性理论给出关于金属塑性行为的更为合理的描述.晶体塑性理论将晶体塑性变形描述为连续滑移的结果，但不考虑位错运动的微观尺度离散性和不均匀性.因此人们对它的滑移描述还存有疑问.

对晶体塑性的计算分析大多采用Hutchinson［1］建议的粘塑性模型，滑移系的启动取决于局部应力场下滑移系分解剪应力的大小(一般由Schmid定律τ(α)=P(α)*:σ［2］计算确定).对该理论用于金属塑性滑移分析的合理性验证，往往只是通过试样应力应变响应来加以间接证实.而晶体滑移很容易在晶体拉伸试样表面观察到，加载前经过仔细研磨和抛光，加载进入塑性状态后就可在试样表面观察到大量的滑移痕迹，而且滑移花样呈现很强的规律性.

多晶材料在平均意义上的力学行为通常可由单晶力学性质计算得到，Taylor［3］曾提出用单晶体的力学性质估算多晶体拉伸性质的模型和计算方法.由于晶粒的尺寸和随机取向不同使这些晶粒在外载荷作用下的各向异性变形与晶粒的晶体结构密切相关.因此金属材料的变形实际是众多取向不同的晶粒的复杂滑移变形的集合，在加载过程中多晶材料的表面会出现离散的滑移带.笔者利用晶体塑性模型对晶体滑移在试样表面留下的滑移带痕迹进行了数值模拟，结合多晶试样在试验过程中的滑移带形貌，对FCC多晶铜试样在单轴拉伸下试样表面滑移带的走向进行晶体塑性分析，通过计算应力激活的晶体滑移面与试样表面的交线来模拟试样表面可观测的滑移带，并且采用统计的方法研究了多晶体内部微观应力、应变的分布.以此来验证晶体塑性有限变形计算方法用于多晶金属塑性滑移分析的合理性.

1 考虑滑移变形机制的多晶材料分析模型

1.1 晶体的滑移变形及其粘塑性描述

采 用 Hill 和 Rice［4］，Asaro 和 Rice［5］以 及Hutchinson［1］建立和发展的晶体塑性理论来描述晶体的塑性变形.且采用Hutchinson［1］提出的晶体滑移变形粘塑性公式来描述

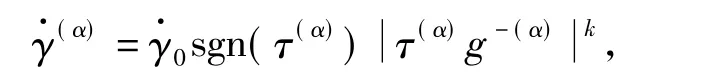
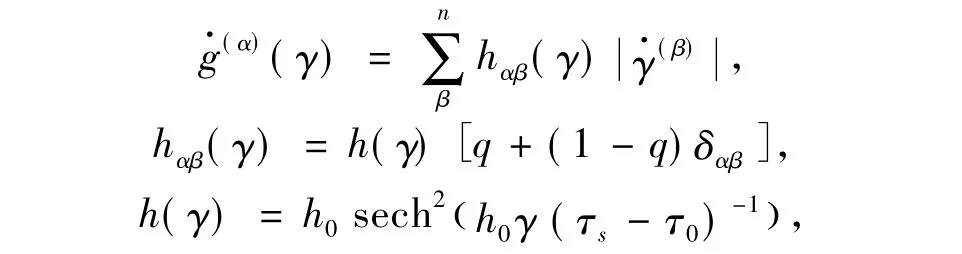
式中:hαβ为滑移硬化模量;n为晶体滑移系的数目;q为常数，一般取1≤q≤1. 4;h0为初始硬化率;τ0为初始临界分解剪应力且g(α)(0)=τ0;τs为临界分解剪应力的饱和值.

1.2 材料的力学性质及试样的几何尺寸

表1 FCC八面体滑移系的滑移面法向矢量与滑移系方向矢量

1.3 多晶试样的晶粒分布、有限元划分与边界条件

多晶试样分析模型中，晶粒形状、取向均按无择优倾向的方式随机生成.该模型包含100个晶粒，假设各晶粒具有相同的各向异性性质，不考虑晶界厚度和材料的微孔洞、微裂纹.有限元模型及晶粒分布如图1所示，模型共有25 000个八节点六面体单元(C3D8r)、30 906个节点.

图1 有限元模型及晶粒分布

边界条件的设置采用了宏观均匀变形的假设，即边界表面变形后仍然保持为平面，保证了模拟物体的宏观连续性.该边界条件设置可通过Abaqus软件对指定节点集的应用约束方程实现.

2 多晶铜单轴拉伸试样滑移变形分析与结果

图2给出了多晶试样模型模拟分析得到的宏观单轴应力－应变曲线，另外还给出了单晶分别在［100］，［110］和［111］方向单轴拉伸的应力应变曲线.由图2可知，晶粒随机分布产生的平均效应使得多晶体的硬化特性高于单晶软位向的拉伸结果而低于单晶硬位向的拉伸结果.

图2 单轴拉伸的应力－应变曲线

多晶试样加载后，各晶粒的滑移系启动，启动的晶体滑移面与试样表面相交.采用几何方法［7］，根据整体坐标系下各滑移面方程以及各个晶粒在加载过程中所激活的具体的滑移系，可计算得到多晶试样表面的滑移线.图3给出了单轴拉伸下多晶铜试样表面的滑移带，图3(a)给出了计算得到的多晶铜试样表面的滑移线，图3(b)为多晶铜单轴拉伸试验的金相显微镜照片.由图3(a)可知，各晶粒启动的滑移系不同，在试样表面产生的滑移带痕迹有明显的区别.对比图3(a)和(b)可知，计算所得的各个晶粒的滑移带与试验照片所示的滑移带痕迹花样比较吻合.各晶粒滑移带的不同主要由于各晶粒初始取向的不同以及拉伸过程中晶格发生旋转，滑移系位向改变造成.而滑移带的不均匀是材料内部变形不均匀在表观显现的一种典型现象.

3 多晶铜单轴拉伸试样应力、应变的不均匀分布分析

由于单晶晶粒的各向异性与随机取向，多晶体内部弹性变形、塑性变形及应力都是不均匀的.图4给出多晶体宏观纵向名义应变为0.1时，材料内部纵向应变按体积分数计算的统计分布.从图4可知多晶试样内纵向应变的分布符合高斯分布的特点，尽管处于宏观均匀状态，其最大值和最小值仍相差很大.图5给出了材料内部纵向应力按体积分数计算的统计分布.从图5可见多晶试样内部极度的不均匀变形导致了局部微观应力很不均匀.

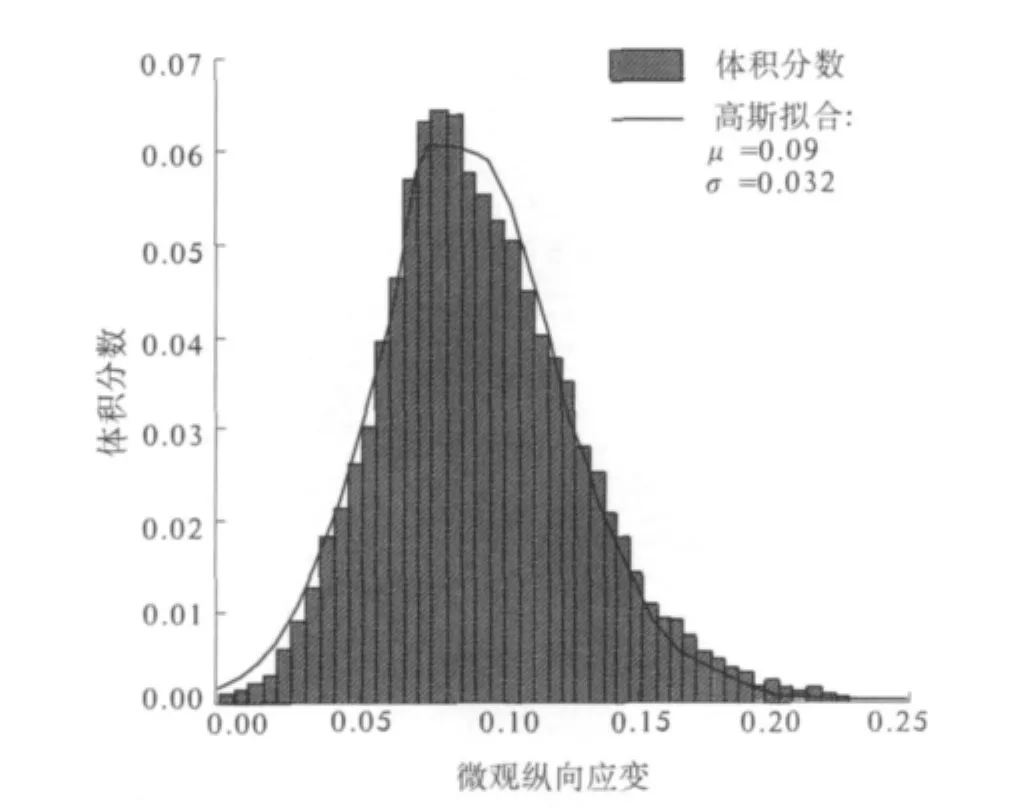
图4 多晶试样内纵向应变统计分布

4 结语

考虑多晶铜试样的单轴拉伸过程，首先对试样变形前的初始金相结构进行了观测，在试样加载之后取得了清晰的晶体滑移形貌.同时对晶体滑移在试样表面留下的滑移带痕迹进行了数值模拟，并对拉伸过程中材料内部的应力、应变的不均匀分布进行了初步统计分析.分析采用建立在晶体塑性理论基础上的晶体塑性有限变形计算方法，通过对多晶铜试样的拉伸变形三维模拟和滑移痕迹的几何计算，得到了以下主要结果.

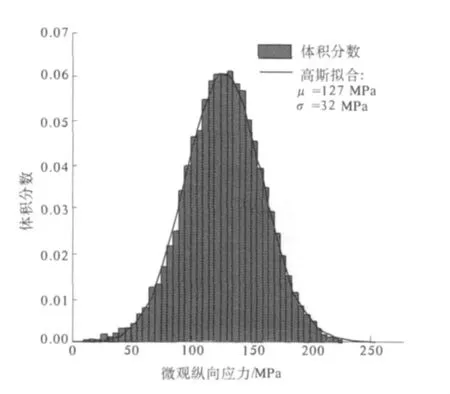
图5 多晶试样内纵向应力统计分布

1)计算所得到的试样表面各个晶粒内部的滑移带痕迹走向不同，所表现的模式与试验现象较为吻合.

2)多晶试样内部纵向应变和纵向应力的统计分布具有高斯分布的特点.

3)多晶试样虽处于宏观均匀变形状态，其内部的应力、应变表现出强烈的不均匀性:纵向最大应变超过了其均值的3倍，纵向最大应力超过了其均值的2倍.

4)证实了用单晶滑移本构关系来模拟多晶金属材料力学行为的可行性.

上述结果表明，将建立在连续滑移描述基础上的晶体塑性理论运用于数值模拟，能够较合理地呈现多晶试样拉伸的表面滑移带痕迹，能够考虑材料内部结构不均匀而引起的宏观响应.

［1］Hutchinson J W.Bounds and self-consistent estimates foe creep of polycrystalline materials［J］.Proceedings of the Royal Society of London A，1976，348:101 －127.

［2］Schmidt E，Boas W.Plasticity of Crystals［M］.London:Chapman and Hall，1935.

［3］Taylor G I.Plastic strain in metals［J］.J Inst Metals，1938，62:307－324.

［4］Hill R，Rice J R.Constitutive analysis of elastic-plastic crystal at arbitrary strain［J］.Journal of the Mechanics and Physics of Solids，1972，20:401 －413.

［5］Asaro R J，Rice J R.Strain localization in ductile single crystal［J］.Journal of the Mechanics and Physics of Solids，1977，25:309 －338.

［6］Hirth J P，Lothe J.Theory of Dislocations［M］.2nd edition.New York:John Wiley ＆ Sons，1982.

［7］石艳柯，张克实.铜单晶拉伸试样表面滑移带花样的晶体塑性分析［J］.固体力学学报，2011，32(6):557－565.

Study of Slip-band of Crystalline Grains on the Surface of Polycrystalline Tensile Specimen

SHI Yan-ke1，ZHANG Qing-hua1，ZHANG Ke-shi2
(1.North China Institute of Water Conservancy and Hydroelectric Power，Zhengzhou 450011，China;2.Guangxi University，Nanning 530004，China)

The paper numerically researches slip-band traces caused by uniaxial tension on the polycrystalline copper specimen surface，by adopting the finite deformation algorithm based on the crystalline plasticity theory.The inhomogeneous distribution of the strain and stress in the tensile specimen are statistically analyzed.The deformation of the polycrystalline copper specimen is simulated by the three dimensional FEM.Through the geometric analysis of intersection-lines between the plastic sliding surface and the specimen surface，the different slip-band traces of the specimen surface are obtained.According to the results，it is confirmed that the crystal plasticity theory based on the description that the crystal plastic deformation is caused by a continuous slip can be applied to the numerical simulation，which is able to reasonably demonstrate the slip-band traced on the surface of the tensile polycrystalline sample，and as well as take into account the macro response caused by the heterogeneity of the material internal structure.

crystal plasticity theory;slip-band trace;inhomogeneous;numerical simulation

1002－5634(2012)02－0031－04

2012－01－15

华北水利水电学院高层次人才科研启动基金项目(2012021，2012020).

石艳柯(1983—)，男，河南鲁山人，讲师，博士，主要从事结构和材料的宏微观力学行为方面的研究.

(责任编辑:蔡洪涛)