基于滑模PI控制交流变频钻机旋转系统

李琳，雷蓓

（西安石油大学 陕西省钻机控制技术重点实验室，陕西 西安 710065）

钻井过程中很多不确定因素，如：地层复杂性、隐蔽性及钻机的运行特性等会引起钻机旋转系统的粘滑振动[1]，影响钻头的跟随性，即在转盘以恒速运行的状态下，钻头速度在0～6倍的钻杆旋转速度之间瞬变，从而导致钻杆疲劳、钻杆组合故障、井眼不稳定及钻头损坏等事故的发生。

针对粘滑振动引起的系统不稳定性问题，已经探究了相关的建模，并对驱动系统及其控制策略进行了研究。在钻杆特性的建模方面，大多数研究都是将钻杆等效为一个具有不同自由度的扭力摆体，建立集中参数模型[2-7]，同时考虑了钻杆组件之间及钻杆和地层之间形成的摩擦效应[8]。在驱动方面，大多数都采用直流电机作为驱动，忽略了交流电动机的优点，为此本文采用交流变频异步电动机作为驱动，通过有效地控制电机的输出特性，保证对钻头良好的过载保护特性和控制作用等特点[9]。在控制策略方面，采用了滑模PI控制，有效地抑制钻井过程中的粘滑振动和各种干扰。

在钻机的运行过程中，由于运行特性变化及存在的干扰问题，使系统存在很多不确定的和变化的参数，文中提出的滑模PI控制策略，将其应用到钻机交流调速旋转系统中，通过仿真验证了控制方法良好的控制性能。

1 钻机旋转系统

钻机旋转系统是石油钻机重要组成部分，它的主要作用是提供足够的转矩和转速，实现钻头和钻具的旋转钻进。钻机旋转系统工作过程为：电动机经齿轮箱传动带动转盘，转盘通过方钻杆来带动钻柱，从而实现钻头旋转钻进，同时钻井液持续循环到井底再返回地面，将切削物带出。钻井液还具有冷却和润滑钻头的作用，并控制着井底压力。为研究钻机旋转系统，首先要建立其数学模型。

1）数学模型

钻机旋转系统可用一个扭摆体来描述，主要部件是由两个具有衰减惯性的机械装置，通过一个弹性的钻杆连接，如图1所示。假设钻杆是同质量的，整个长度简单的被认为是一个单线性直线弹簧系统，弹性系数为K，没有横向运动。

钻机旋转系统的数学模型分别由钻井底部装置运动方程，驱动系统运动方程以及钻头摩擦力方程来描述。

① 低速（钻井底部装置）运动方程

低速运动方程可表示为

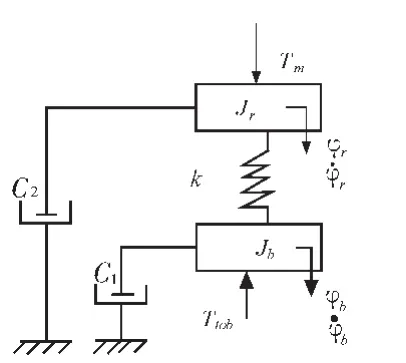
图1 钻机旋转系统简化模型Fig.1 Drilling rotary system model

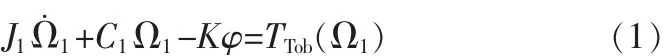
式中，φ=φ2-φ1，Ω1=和 Ω2=， 其中 φ1是钻头的角位移，rad；φ2是旋转面的角位移，rad；J1是轴和钻杆的转动惯量，kg·m2；C1是 BHA 衰减阻尼系数，N·m·s/rad；Ttob是同钻头力矩相关的非线性函数，N·m。

②驱动系统运动方程

驱动系统的机械系统特性由3部分构成：转盘、倾斜的齿轮箱和交流电动机。其系统运动方程为：

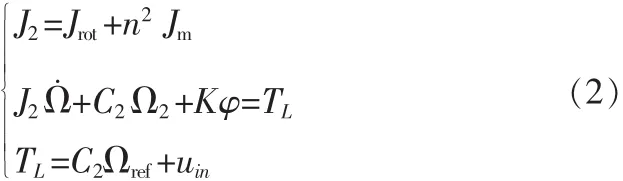
式中，J2为折合到转盘的等效转动惯量，kg·m2；Jrot和Jm分别为转盘和电机的转动惯量，kg·m2；C2为转盘衰减系数，N·m·s/rad；Ωref为交流电动机的输出转速，rad/s；TL是交流电动机的负载转矩，N·m。

③摩擦力矩方程

摩擦力矩Ttob是钻头上的反力矩和钻井底部装置上的非线性摩擦力矩之和，Ttob作为钻头速度的函数由以下非线性函数给出[7]：

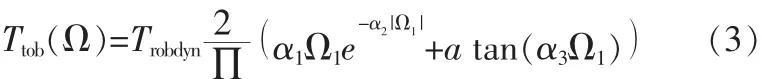
式中，Trob（dyn）为动摩擦力矩，N·m ，这里Trobdyn=0.5 kN·m，α1=9.5，α2=2.2，α3=35。摩擦力矩与钻头角速度关系如图2所示。

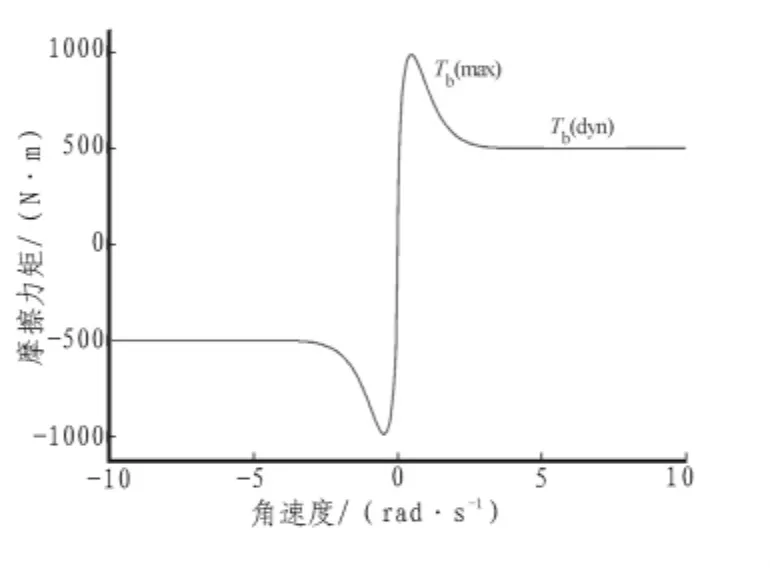
图2 摩擦力矩与钻头加速度的关系Fig.2 Torque and the angular velocity at the bit

从图2可以看出，钻井过程中钻头角速度接近零时，摩擦力矩会很大，这是产生钻头粘滑振动的主要原因。

2）钻机旋转控制系统

石油钻机是具有复杂动力学特性的机械系统，系统本身的运行特性、地层及岩石结构的复杂性、钻杆长度变化都会引起有害振动，使钻机设备发生故障，使钻头不能旋转甚至容易失速。为了抑制这些有害振动，针对交流变频异步电动机驱动系统，设计滑模PI控制器，可增强系统的鲁棒性，有效抑制钻机旋转系统的粘滑振动。钻机旋转控制系统方框图如图3所示。

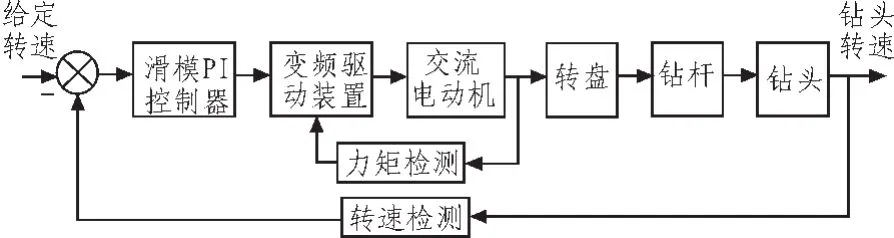
图3 旋转控制系统方框图Fig.3 Rotary control system

2 控制系统的设计

1）输入状态线性化控制器的设计

针对钻机旋转系统，首先设计其控制器。式（2）～（3）给出的钻机旋转系统的运动方程为非线性方程，为了减少计算量，将钻机旋转系统非线性方程推导为线性方程，求出的输入状态线性化控制器为[10]：

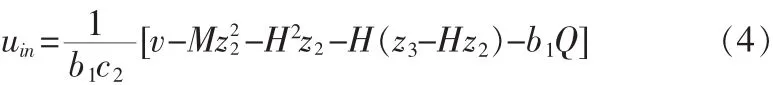
式中，

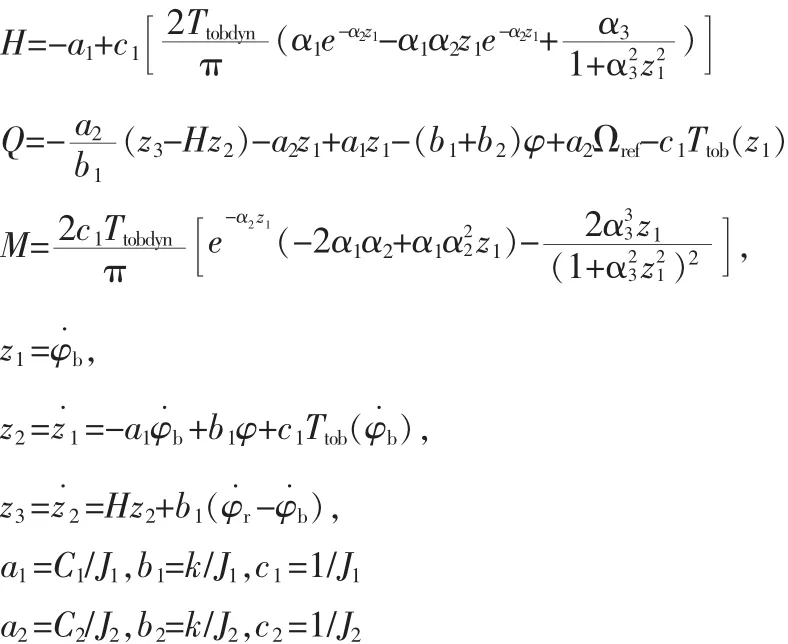
2）滑模控制器设计

从图3可以看出，交流变频电动机驱动转盘，再由转盘经钻杆带动钻头，为了提高钻头的稳定性和鲁棒性，引入滑模控制，设计滑模控制的关键在于开关面函数的选取。

交流电机的转矩方程为：

式中，Te为电磁转矩，N·m；TL为负载转矩，N·m；ωr为转子转速，rad/s；J为转动惯量，kg·m2。

定义开关面函数为：

式中，ω为钻头转速，rad/s；ω*为交流电动机提供转速，rad/s；λ为正常数。速度环PI调节器采用滑模PI控制器，则滑模控制器设计为：

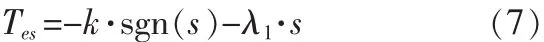
PI控制器设计为：

式中，λ1、k为正常数，KP为比例系数，KI为积分时间常数。因而，转速控制器为：

3 仿真实验

对设计的基于指数趋近律滑模PI控制的交流调速旋转系统进行仿真，钻机旋转系统采用典型参数[11]。在基于指数趋近律PI控制下和滑模PI控制下钻头角速度阶跃响应分别如图 4（a）、（b）所示。 在仿真过程中，PI控制器参数 KP=1.7，KI=1.5， 滑模控制器参数 λ=0.2，λ1=0.05，k=0.2。

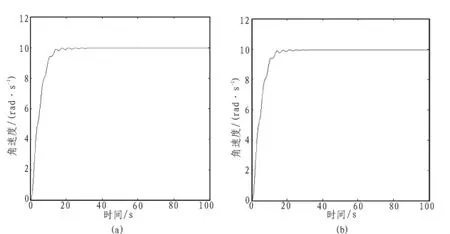
图4 钻头角速度的阶跃响应Fig.4 The step response of the bit angular velocity

由图4可以看出，PI控制下钻头角速度的上升时间为20 s，调节时间为32 s，系统超调和稳态误差趋于0，滑模PI控制下钻头角速度的上升时间为20 s，调节时间为27 s，系统超调和稳态误差趋近于0。即系统静态性能和动态性能很好，可以较好地抑制钻头的粘滑振动，而滑模PI控制可使系统更快速的趋近稳定。

若驱动电机为直流电机，由参考文献[11]可知钻头角速度的阶跃响应如图5所示。

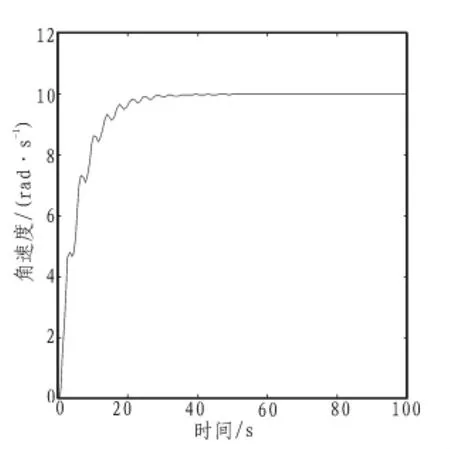
图5 直流驱动方式下钻头角速度的阶跃响应Fig.5 The step response of the bit angular velocity with DC drive

由图5可以看出，不同驱动方式对钻头转速有着明显的影响，若交流电动机电机作为驱动，加速过程中振动减小，趋近速度较快，系统的稳定性更高。

在基于指数趋近律滑模PI控制下，若系统参数 （K）变化，其对钻头角速度的影响如图6所示。

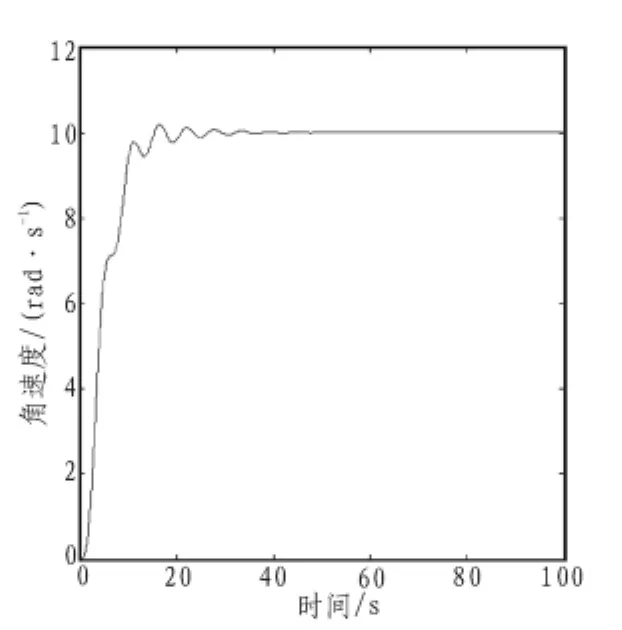
图6 参数变化时钻头角速度的阶跃响应Fig.6 Parameter changes of the step response of the bit angular velocity

由图6可以看出，参数变化对系统响应有稍微的影响，但受滑模控制影响，趋近速度较快，系统短时间也能调节到稳态值。因此，基于指数趋近律的滑模PI控制具有快速的调节能力和鲁棒特性。

4 结 论

建立了以交流电动机为驱动的钻机旋转系统模型。设计了滑模PI控制器，从而提高系统响应速度。钻机旋转系统采用交流电动机作为驱动，与传统的直流电机驱动相比，在实际应用中系统运行更可靠，钻头粘滑振动得到有效的抑制。基于指数趋近律滑模PI控制器结合了滑模控制和PI控制的优点，可以缩短到达滑模面的时间，改善系统的动态响应以及静态响应，提高系统的稳定性和鲁棒性。

[1]Plácido J C R，Santos H M R，Galeano Y D.Drillstring vibration and wellbore instability[J].Journal of Energy Resources Technology，2002，124（4）：217-222

[2]Lin Y Q，Wang Y H.Stick-slip vibration of drill strings[J].Journal of Engineering for Industry，1991，113（1）：38-43.

[3]Yigit A S，Christoforou A P.Coupled torsional and bending vi-brations of actively controlled drillstrings[J].Journal of Soundand Vibration，2000，234（1）：67-83.

[4]Navarro-López E M，Suárez-Cortez R.Vibraciones mecánicas enuna sarta de perforación：Problemas decontrol[J].Revista Ibe-roamericana de Automática e Informática Industrial，2005，2（1）：43-54.

[5]祝效华，刘清友，童华.三维井眼全井钻柱系统动力学模型研究[J].石油学报，2008，29（2）：288-291.

ZHU Xiao-hua，LIU Qing-you，TONG Hua.Research on dynamics model of full hole drilling string system with three-dimensional trajectory[J].Acta Petrolei Sinica，2008，29（2）：288-291.

[6]刘金梅，周国强，韩国有.基于有限元动力模型的在役钻机井架仿真模型[J].石油学报，2009，30（5）：788-792.

LIU Jin-mei，ZHOU Guo-qiang，HAN Guo-you.Simulation model for in-service rig derrick based on finite dynamic model[J].Acta Petrolei Sinica，2009，30（5）：788-792.

[7]Serrarens A F A.H∞ control as applied to torsional drillstring dynamics[D].Msc.Thesis，Eindhoven University of Technology，2002.

[8]Mihajlovic N，van Veggel A A，vandeWouw Netal.Analysis of friction-induced limit cycling in an experimental drillstring system[J].Journal of Dynamic Systems，Measurement and Control，2004，126（4）：709-720.

[9]桂暖银，刘宝林，郑黎明.安全钻探新途径-交流变频调速动力系统应用前景展望[J].探矿工程，2009（4）：1-3.

GUI Nuan-yin，ZHENG Li-ming，LIU Bao-lin.New way to safe drilling[J].Exploration Engineering，2009（4）：1-3.

[10]Abdulgalil F，Siguerdidjane H.PID based on sliding mode control for rotary drilling system：The international conference on computer as a tool[C]//United States：Inst.of Elec.and Elec.Eng.Computer Society，2005.

[11]Navarro-López E M， Cortés D.Sliding-mode control of a multi-DOF oilwelldrillstringwith stick-slip oscillations：American control conference[C]//New York：Institute of Electrical and Electronics Engineers Inc.，2007.