GPS信号快速捕获技术研究及仿真

于雪晖，徐 京，柳 涛

（北京卫星信息工程研究所 北京 100086）

目前，GPS（Global Positioning System）系统被广泛地应用于民用和军事部门，提供定位、测速和授时服务。GPS在L1（1 575.42 MHz）频率上提供标准定位服务（SPS）。 每颗 GPS卫星有一个唯一的扩频码（C/A码），在用户端每颗卫星的C/A码是已知的。GPS接收机需要搜索这些C/A码，确定当前哪些卫星是可用的[1]。对于每个码，接收机要执行二维的搜索，即搜索载波频率偏移和码相位偏移，也就是捕获C/A码，捕获后接收机要跟踪该信号。信号捕获是GPS接收机中最耗时的操作，因此，C/A码信号的快速捕获也逐渐成为研究的热点课题。

Van Nee[2]提出了一种快速的搜索算法（并行码相位搜索捕获算法），该方法利用基于FFT的相关器，在一步内搜索所有可能的码相位偏移，并用频域乘法进行相关运算。在此方法的基础上，采用两步信号处理的方式，减少一级数据采样点，再对已得到的粗单元进行细分，将频率分辨率控制在100 Hz左右。相对于传统的并行码相位搜索捕获算法，在减少了信号捕获的运算量的同时提高了频率分辨率，由此提高了信号捕获速度并减小了相关峰值衰减[3]。

1 捕获原理与算法

1.1 GPS信号数学模型

采用基于FFT的并行码相位快速捕获方法完成对卫星信号的捕获，对卫星信号的捕获实质上还是一个二维搜索的过程，一个是对码延迟的搜索，另一个是对多普勒频移的搜索。

经过射频模拟下变频和数字下变频后，接收到的卫星信号可以表示为：

其中A为信号幅度，C（t）为接收信号的 PRN 码，D（t）为导航数据信息，频率为50 Hz，τ为信号延迟，fd为多普勒频率，φ0为初始相位，ξ（t）为接收机噪声，服从正态分布。

1.2 并行码相位捕获原理

当数字中频信号分别与I支路和Q支路上某一频率的复制正弦和复制余弦载波信号混频后，并行码相位搜索捕获算法对混频结果进行傅里叶变换，然后将变换结果与复制C/A码信号傅里叶变换的共轭值相乘，接着将所得的乘积经傅里叶反变换得到在时域内的相关结果，最后对这些相关值进行检测来判断信号是否存在[4]。

根据卫星信号（1）式，设多普勒频移估计值为fˆd，那么首先对y（tn）信号进行多普勒去除，然后再与复现的C/A码作相关运算，如式（2）所示。

其中 d为码延迟，ts为采样时间间隔，C（m-d）为 C/A码的循环移位。

对 Z（d，l）做离散傅里叶变换：

因为C/A码为实数，所以：

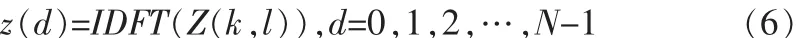
对上式取反傅里叶变换那么，z（d）即为码延迟为 d，归一化多普勒为 l时的相关值。

根据上面的讨论，当复现的C/A码与实际接收信号的C/A码完全对齐，并且 l=[Nfdts]时相关结果z（d）取得最大值，[x]表示取不大于x的最大整数。此时，码延迟的估计值为d，多普勒的估计值为：

其中，N为DFT的点数，fs为采样频率，fs=1/ts。

根据（7）可知，多普勒频移的频率分辨率为：

由式（8）可知，在采样频率一定时，DFT的点数越大，多普勒频移的频率分辨能力就越高。

1.3 相关峰值衰减

相关峰值的损耗主要来自于两个方面，码片分辨率和频率分辨率。第一由于对PRN码进行了采样，码片分辨率的精度受到采样率的影响，进而影响相关峰值，相关峰值的损耗为：

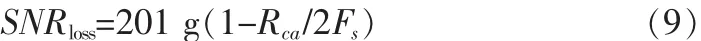
第二方面来自于残余的多普勒频偏，即频率分辨率，当如式（1）的数字中频信号经过混频后，在进行码相关的积分时，会产生一个幅度的调制系数 sin c（T），如式所示：

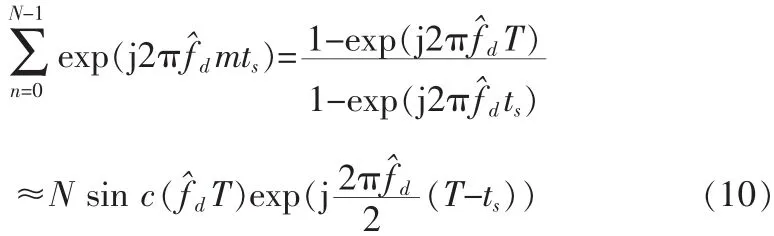
因此，当频率有偏移时，相关峰值能量的损失SNRloss2为201 g[sin c（T）]。

2 算法设计及实现

本文采用Matlab设计工具进行算法设计与实现。如图1所示为并行码相位捕获算法流程图。首先，根据已知的载波频率和伪码产生原理复现本地数字中频载波信号和伪随机码（C/A码）信号；再将本地载波与接收到的中频信号进行混频，剥离载波信号；然后将C/A码信号和混频后的信号在频域进行乘法运算，再进行傅里叶反变换，在时域得到相关峰值所对应的载波频点和码相位[5]。至此，第一次粗搜索进行完毕，但由于500 Hz的频率分辨率太低，不利于后续的信号跟踪，所以要进行第二次精搜索。

第二次搜索只对已经捕获到的信号即相关峰值超过预定门限的信号进行搜索，根据上述求得的C/A码相位，可以得到剥离C/A码后的载波信号，再将捕获到的粗单元进行细分，重复上述计算，增加数据长度将频率分辨率调至100 Hz，这样只需求得该载波信号在频域中最大功率值所对应的频点[6]，即为载波频率。根据以上的相关峰值衰减的理论分析可知，在码相位分辨率不变的情况下，频率分辨率从500 Hz提升到100 Hz，相关峰值衰减可以减小3.78 dB，增大了信号捕获的概率，提高了捕获性能。

3 仿真结果

1）仿真条件

为验证捕获算法的有效性，以一段实测的GPS信号作为数据源，该GPS射频信号首先通过射频前端的下变频、滤波和放大到中频为9.548 MHz的信号，然后以38.192 MHz的采样率进行数字化，量化位数为8-bit，由于C/A码信号带宽为2.046 MHz，因此38.192 MHz采样率满足奈奎斯特采样定理。经数字化后，每1 ms采样时间内有38 192个C/A码采样点，从这里开始利用该算法对C/A码进行搜索和捕获。

2）仿真结果及分析

以21号卫星为例，仿真结果如图2所示。从图中可以得到相关峰值的C/A码相位起始位置在采样点的第13 404点处，最大频率分量出现在载波频率为9 547.5 kHz处，此时得到的载频有较低的频率分辨率，细化频率后得到其精细载频为9 547.426 kHz，满足跟踪环所需的频率分辨率在几十赫兹以内的要求。

图3所示为32颗卫星的捕获结果，全部卫星捕获完毕后将测量值（峰值与次峰值的比值）与捕获门限进行比较，超过门限则判为捕获可以进一步转为跟踪，未超过门限则视为无法捕获[7]。

图1 并行码相位捕获算法流程图Fig.1 Flow chart of parallel code-phase acquisition method

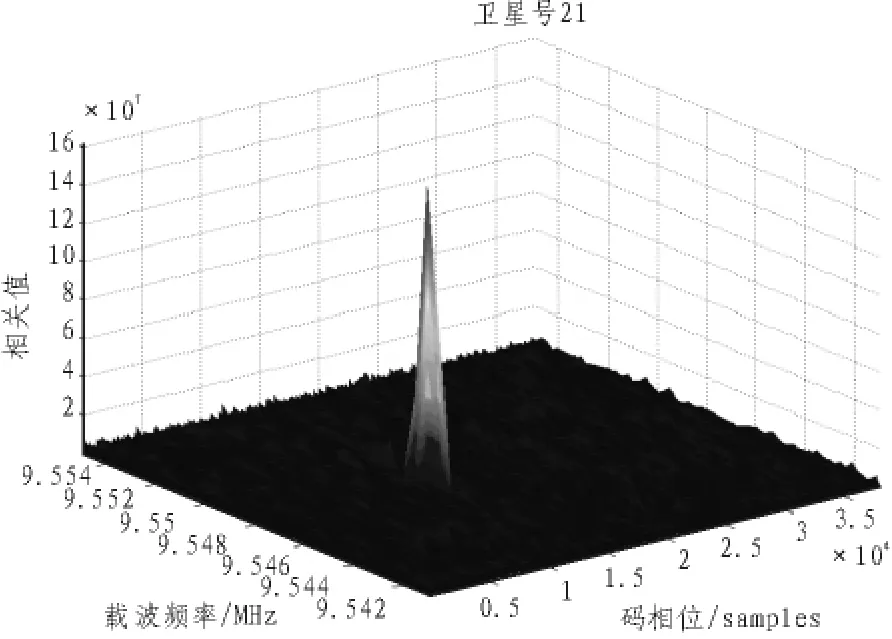
图2 21号卫星信号仿真结果Fig.2 Simulation result of GPS21 signal

实验中采样频率为38.192 MHz，因此，1 ms内得到的采样点为 38 192个，对于 FFT运算要进行补零，即 N′=N+n=38 192+273 44=65 536=216。在并行码相位捕获算法中进行了两次FFT运算，一次矩阵乘法运算和一次IFFT运算，每次FFT 和 IFFT 运算需要 lbN′×（N′/2）次乘法运算和 N′lbN′次加法运算，矩阵运算需要N′次乘法。若在时域进行传统的顺序搜索捕获，那么要分别进行N2次乘法和加法。因此，可以求得乘法和加法的频域运算次数相对于时域运算次数的百分比分别为：

4 结 论

文中利用Matlab对改进了的并行码相位捕获算法进行了仿真，仿真结果表明采用该种方法可以得到输入信号的C/A码初始位置和载波的精细频率，减小相关峰值衰减量，提高捕获能力，同时将大量相关运算转换到频域进行，极大减少了计算量，相对于时域顺序捕获算法大大提高了信号的捕获速度，能更好地满足高动态接收机的实时性要求。

[1]谢钢.GPS原理与接收机设计[M].北京：电子工业出版社，2009：372-374.

[2]Van-Nee D J R，Coenen A J R M.New fast GPS code acquisition technique using FFT[J].Electronics Letter，1991，27（2）：158-160.

[3]Akopian D.Fast FFT based GPS satellite acquisition methods[J].IEE Proceedings Radar Sonar&Navigation，2005，152（4）：277-286.

[4]Psiaki M L.Block acquisition of weak GPS signals in a software receiver[EB/OL].（2001-09）.http：//citeseerx.ist.psu.edu/viewdoc/download doi=10.1.1.6.6940&rep=rep1&type=pdf.

[5]Nogues-Correig O，Gali E C.A GPS-Reflections receiver that computes Doppler/Delay Maps in Real Time [J].IEEE Transactions on Geoscience and Remote Sensing，2007，45（1）：156-174.

[6]Nunes F D，Leitao J M N.A new fast code/frequency acquisition algorithm forGPS C/A signals [C]//Vehicular Technology Conference，2003（2）：766-770.

[7]Lin D W，Tsui J B Y.A software GPS receiver for weak signals[C]//IEEE MTT-S International Microwave Symposium Digest，2001（3）：2139-2142.

[8]李琪琪，叶斌，陈锋.液体火箭发动机试验频率量信号的处理与仿真[J].火箭推进，2008（5）：39-42.

LI Qi-qi，YE Bin，CHEN Feng.Processing and simulating of frequency signal in liquid propellant rocket engine test[J].Journal of Rocket Propulsion，2008（5）：39-42.