二级倒立摆系统的模糊控制

焦灵侠，任海波，郭 敏

（1.西安工业大学北方信息工程学院 陕西 西安 710032；2.西北机电工程研究所 陕西 咸阳 712099；3.榆林学院 能源工程学院，陕西 榆林 719000）

倒立摆是一种典型的高阶非线性、多变量、强耦合、绝对不稳定的实验装置，它具有结构简单、成本低廉、易于调整等特点，作为这样一个被控对象，只有有效的控制策略才能够使其稳定，同时它也是检验各种控制理论的实验平台。倒立摆系统涉及控制理论、计算机控制、机器人技术等多个领域，并且结合了多种技术，因此可以看作是典型的被控对象供科研人员研究。倒立摆系统被广泛应用于双足机器人行走及火箭稳定发射及飞行方面，对于多级倒立摆和复杂结构的倒立摆进行控制更是近年来各科学领域不断研究，创新的问题之一，所以对于倒立摆系统的研究具有深远的意义[1]。

1 二级倒立摆系统数学模型的建立

在忽略了空气阻力和各种摩擦，并认为摆杆为刚体。二级倒立摆示意图如图1所示。

利用拉格朗日方程推导运动学方程：

拉格朗日方程为：L（q，q˙）=T（q，q˙）-V（q，q˙）

其中L为拉格朗日算子，q为系统的广义坐标，T为系统的动能，V为系统的势能，i=1，2，3…n，fi为系统在第i个广义坐标上的外力。系统的广义坐标有3个，分别为x，θ1，θ2。系统的动能：

图1 二级倒立摆示意图Fig.1 Two-stage pendulum schematic diagram

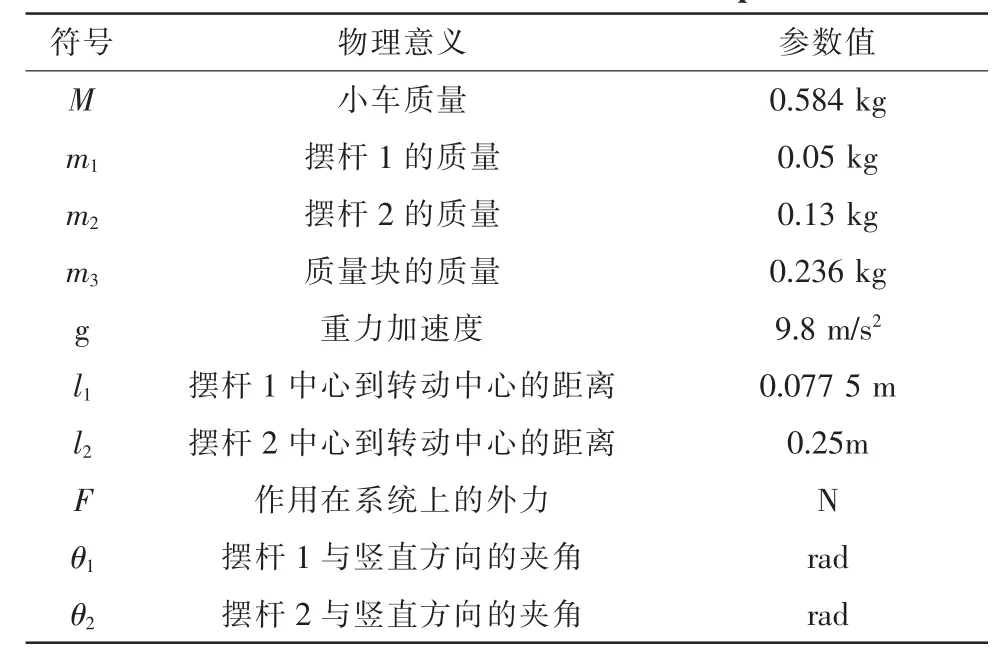
表1 倒立摆参数定义Tab.1 Parameter defines of the inverted pendulum

其中 TM，Tm1，Tm2，Tm3分别为小车的动能， 摆杆 1 的动能，摆杆2的动能和质量块的动能。

系统的动能为：

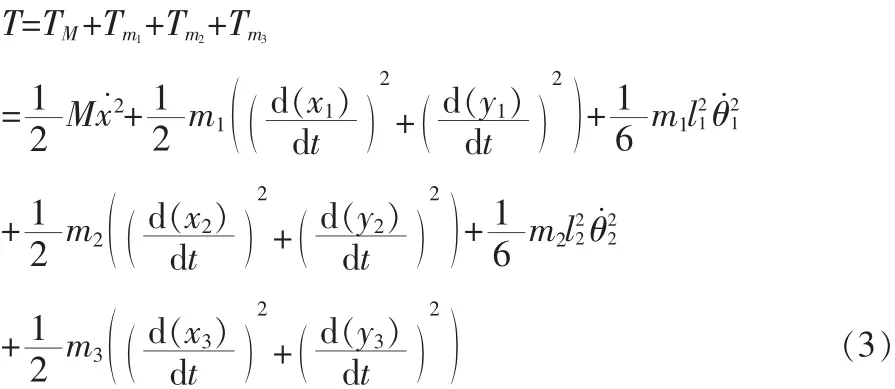
系统的势能为：

系统在θ1，θ2广义坐标下没有外力作用，所以有：

将其在平衡位置附近进行泰勒级数展开，并线性化，有：

带入参数值，系统的状态方程为：

2 二级倒立摆的模糊控制

二级倒立摆的模糊控制[2]采用的控制思想是将多输入/单输出的模糊控制器，分解成一个较简单的多输入/单输出的模糊控制器。通过对模型的仿真，得到最合适的模糊控制参数，量化因子和比例因子ke、kec、ku。在仿真的基础上，设计实时控制程序，在实际的倒立摆实验平台上进行实时控制研究。

2.1 模糊控制器的设计

1）确定输入变量和输出变量

综合误差（小车的位移、上摆的摆角、下摆的摆角）E和综合误差变化率（小车的速度、上摆的角速度、下摆的角速度）EC作为输入变量，电机的控制力u作为输出变量[3]。

利用命令 K=lqr（A，B，Q，R），得到反馈矩阵 K：

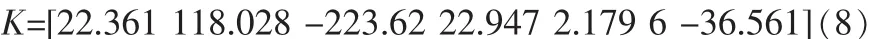
综合误差E和综合误差变化率EC。

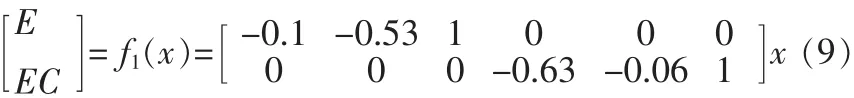
2）E、EC、u 隶属度函数的设计

图2 E和EC隶属度函数曲线Fig.2 Membership function curves of E and EC

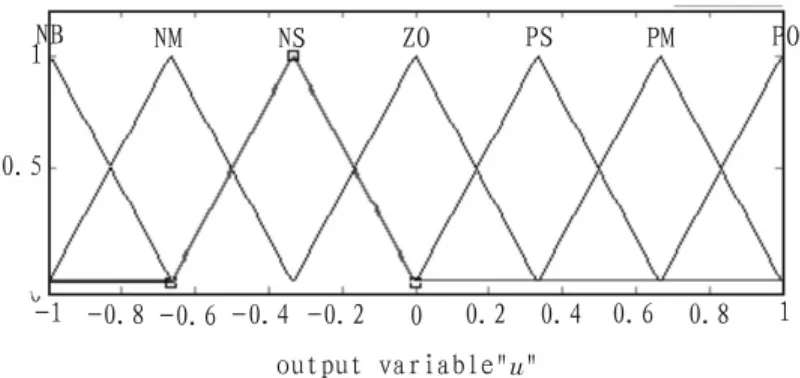
图3 u的隶属度函数曲线Fig.3 Membership function curves of u

3）模糊推理

采用Mamdani最小运算规则。

4）模糊控制规则

根据输入/输出论域上的模糊语言变量划分NB（负大），NM（负中），NS（负小），ZO（零），PS（正小），PM（正中），PB（正大），设计模糊推理规则如表2所示。

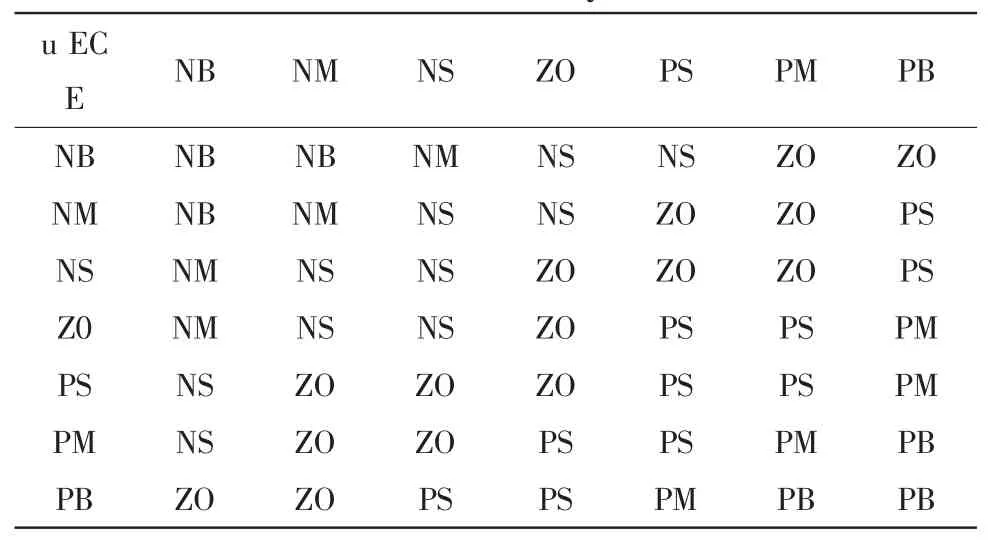
表2 模糊控制规则Tab.2 Rules of fuzzy control

5）解模糊

重心法。

2.2 二级倒立摆系统的实时控制

经过多次仿真，选定了合适的模糊控制器的参数[4-6]，得到了比较理想的曲线，当ke=1.5、kec=1.5、ku=6时控制效果较好，二级倒立摆系统能够得到较好的稳定，小车在0.1 cm位置附近来回振动，下摆摆杆在平衡位置附近摆动，上摆杆在平衡位置小幅度摆动。

根据仿真结果，在实际的倒立摆实验装置上进行实时控制，设计的二级倒立摆实时控制程序如图4所示。

实时控制曲线如图7所示。

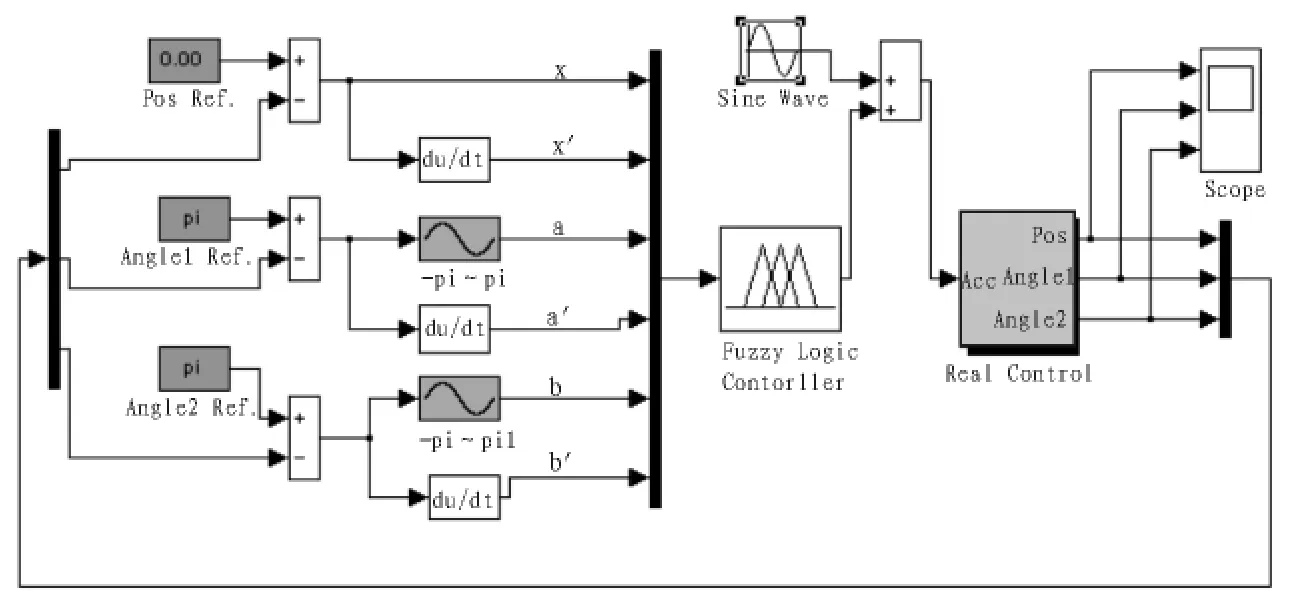
图4 二级倒立摆的实时控制程序Fig.4 Real-time control program of two-stage pendulum

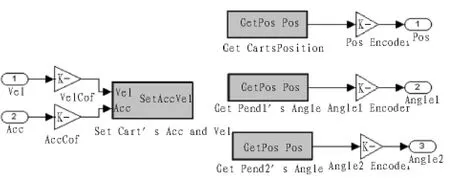
图5 二级倒立摆内部结构Fig.5 Internal structure of two-stage pendulum

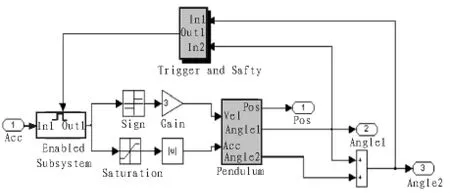
图6 实时控制内部结构Fig.6 Internal structure of real-time control

图7 二级倒立摆系统实时控制曲线Fig.7 Real-time control curve of two-stage pendulum

3 结 论

从二级倒立摆的实时控制曲线上可以看出，小车位移偏离平衡位置的最大距离小于5 cm，上摆角的振动幅值在0.04 rad范围内，下摆角振动幅值在0.08 rad以内，控制的效果比较理想，系统稳定的响应时间在5 s之内。实时控制结果证明模糊控制控制二级倒立摆系统具有很好的稳定性和鲁棒性。

[1]张葛祥，李众立，毕效辉.倒立摆和自动控制技术研究[J].西南工学院学报，2001，16（3）：12-16.

ZHANG Ge-xiang，LI Zhung-li，BI Xiao-hui.Inverted pendulum and automatic control technology [J].Southwest Institute Sinica，2001，16 （3） ：12-16.

[2]曹承志，王楠.智能技术[M].北京：淸华大学出版社，2004.

[3]吴寿章.最优控制理论与应用[M].北京：机械工业出版社，2008.

[4]闻新，周露，李东江，等.MATLAB模糊逻辑工具箱的分析与应用[M].北京：科学出版社，2001.

[5]李岩，姚旭东.二级倒立摆控制系统分析[J].沈阳工业学院学报，1999，18（2）：86-92.

LI Yan，YAO Xudong.Analysis of double inverted pendulum control system[J].Shenyang Polytechnic University，1999，18（2）：86-92

[6]张龙.直线二级倒立摆的稳定控制研究[D].西安：西安建筑科技大学，2008.