城市轨道交通多路径选择研究
2012-07-13赵楠,李超
赵 楠,李 超
(中国铁道科学研究院 电子计算技术研究所,北京 100081)
1 研究背景
目前,深圳轨道交通网络由 5 条线路构成,合计里程 178 km,分别由 3 家不同的运营公司共同管理运营。在无障碍换乘的模式下,如何既能保证整个地铁系统一体化运营,又能公平、公正地维持各运营商的利益,是多家运营商合作的前提,因此要求地铁总公司有一套合理的清分制度保障其正常运营。而路网中有效路径的选择及其对客流的承担比例是地铁清分的重要基础数据,也是地铁中心分配票款的重要依据。本文结合深圳地铁具体情况及调研结果,重点介绍深圳地铁轨道交通多路径选择模型算法及模型参数标定。
2 深圳地铁布局
深圳地铁开通运营线路如图 1 所示,5 条线路形成网状连接,其中 1 号线、2 号线和 5 号线分别由西北、东北向东横穿城市;3 号线、4 号线由北向南纵贯城市。车站编号的顺序为从 1 号线到 5 号线,共 118 个车站,其中换乘站 13 个。由于换乘站较多,乘客从某车站出发到达另一条线的其他车站有多种选择路径。综合考虑列车发车间隔、旅客换乘步行时间、列车运行时间和车站停车时间等因素,可初步确定车站间的有效路径;根据建立的模型可计算出两个车站间不同有效路径的旅客比例,并将此数据提交地铁清分中心提供清分依据。
3 路径选择因素分析
在无障碍换乘的模式下,影响城市轨道交通运费清分的因素多而复杂,可以概括为旅客本身因素、旅客出行特征因素、轨道交通网络因素和其他方面的因素。每一影响因素又包括很多的具体指标,如旅客本身因素主要包括年龄等;出行特征因素主要包括出行距离、出行目的和是否高峰出行等;网络因素主要包括线网结构、出行时间、路径换乘形式和运营时间等;其他方面因素主要包括票价和对运营商的偏好等。其中,旅客出行特征因素作为关键因素,主要包括以下指标。
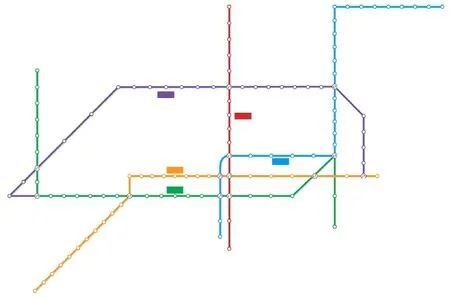
图1 深圳地铁线路图
(1)出行距离。出行距离是指旅客一次轨道交通的出行距离。不同的出行距离对旅客选择路径具有一定的影响。例如,长距离出行时,旅客一般希望能够通过换乘来节约总出行时间;而对于短距离出行,旅客一般都不希望换乘。
(2)出行目的。不同出行目的旅客对路径的选择也不同。例如,以购物、休闲、游玩为目的的旅客一般不会太在意出行时间的长短,而更重视出行中的方便舒适度;而上下班或公务出行时旅客对时间比较敏感,更希望能够通过换乘来节省总出行时间。
(3)出行时段。出行时段包括客流高峰与平峰时段。在客流高峰时段,由于上下车人数很多,车厢内和车站的旅客也很多,很难保证一次候车就有机会上车,而且每次换乘时上下车不方便,还有可能需要步行一段距离,消耗体力和时间,因此,旅客希望选择换乘次数少的路径,对于时间的敏感度不是很高。
(4)拥挤程度。拥挤程度主要是指路径的平均拥挤程度。该因素影响旅客对于出行路径的选择,进而影响运费清分。在深圳市旅客出行调查中,13% 的人选择拥挤程度为最重要的因素。在清分模型中可以采用列车的容纳能力和需要服务的旅客总量的比例来量化此因素。
通过对深圳地铁的 2 000 份问卷调查可知,48% 的旅客会选择总出行时间最短的出行方式,42% 的旅客会选择换乘时间最少的出行方式,5%的旅客会选择经过站点数最少的出行方式。由调查数据可知,旅客出行路径选择关注的最重要因素是总出行时间最短和换乘次数最少,较重要因素是拥挤程度,这 3 项因素是构建模型的主要参数指标。
4 模型构建
目前,模型主要有正态分布概率模型和 Logit模型。结合深圳地铁实际情况,在对比正态分布概率模型和 Logit 模型后,发现采用正态分布概率模型时的测算结果更符合深圳地铁的调查问卷结果,以下主要介绍基于正态分布的多路径模型。
4.1 正态分布概率模型
路径的选择概率是以各路径的修正综合阻抗值为基础,按照一定的统计规律,确定各有效径路分担某一 OD 客流的比例。①当有效路径集的元素惟一时,该有效路径是惟一的绝对最优解,承担100%的客流。②当有效路径集的元素不惟一时,就产生了客流如何在各条路径中分配的问题,基本理念是根据旅客选择路径的概率计算客流的路径分配比例。
(3)1≥P1≥P2≥…≥Pk≥0,即阻抗值越大的路径被选择的概率越小,其中最小阻抗值路径被选择的概率最大。
(5)随着阻抗值的增加, Pi的递减速率将迅速增加,即路径被选择的概率将迅速减少。实际上,旅客对乘坐时间的较大延长会比较敏感。
概率计算中常用的正态分布函数能够很好地满足上述要求,其函数公式为:
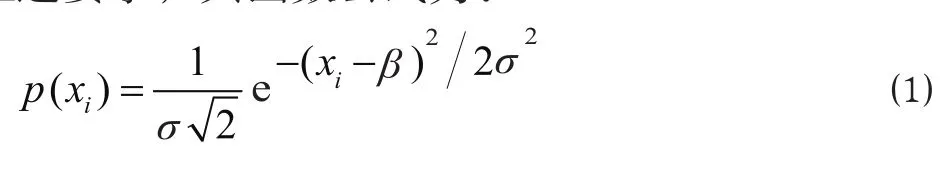
式中:β 为得到概率最大期望的 x 值,在这里为 0;e 为自然对数的底,约等于 2.718;σ 是一个常数,其值决定正态曲线的变化程度。随机变量 xi取为其中 :α 为旅客在出行过程中对换乘时间的敏感度;μ 为旅客在出行过程中对出行时间的敏感度;为第 i 条有效路径的换乘时间,min;为第 i 条有效路径的总出行时间,min。由于不可能权值小于最小阻抗值min的路径,因此,只需要取正态分布曲线x≥μ的正半部分。
σ是公式中的参数,对于所有 OD 对是一个常数。它在数学上的意义非常明确,但是很难直接赋予某种实际意义。可以通过实际旅客出行路径选择的交通调查结果分析拟合出参数σ的值。则路径的分配比例可用以下公式计算:
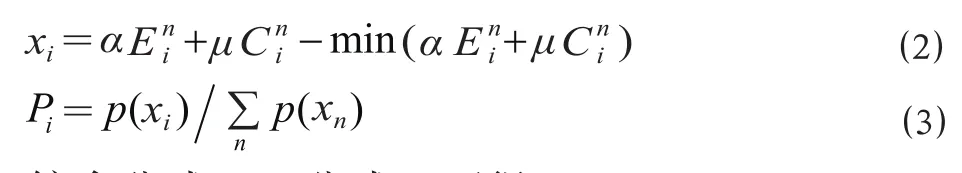
综合公式⑴~公式⑶可得:
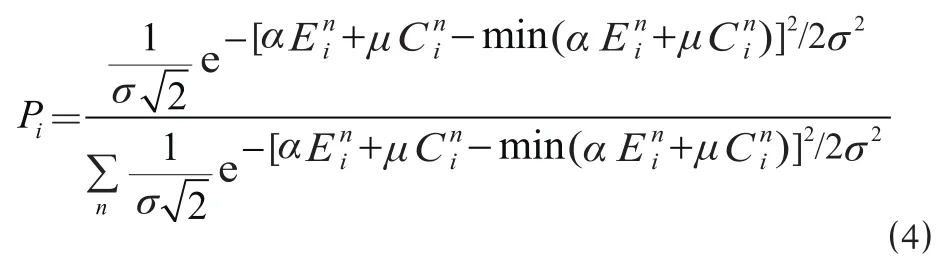
通过选择合理的σ参数,采用公式⑷的概率分布函数可更加接近实际地反映旅客的路径选择行为,而且能够适应 OD 对之间有效路径的不同数量和组合类型,满足Pi的上述 5 个特性。
4.2 正态分布概率模型参数标定
在正态分布概率模型中,需要标定的未知参数为α、μ、σ。其中,σ反映了旅客在实际选择有效路径时,具有出行时间越短旅客选择概率越大,出行时间增加时路径被选择的概率明显下滑的规律;而α表现出换乘会减少选择概率的现象。在标定时利用深圳市旅客轨道交通出行选择情况,参数值如表 1 所示。
根据表 1 调查数据验证路径选择概率模型的有效性,统计拟合参数如表 2 所示。
为验证正态分布模型及其参数估计的有效性,利用实际调查数据与模型计算结果进行比照,结果如表 3 所示。
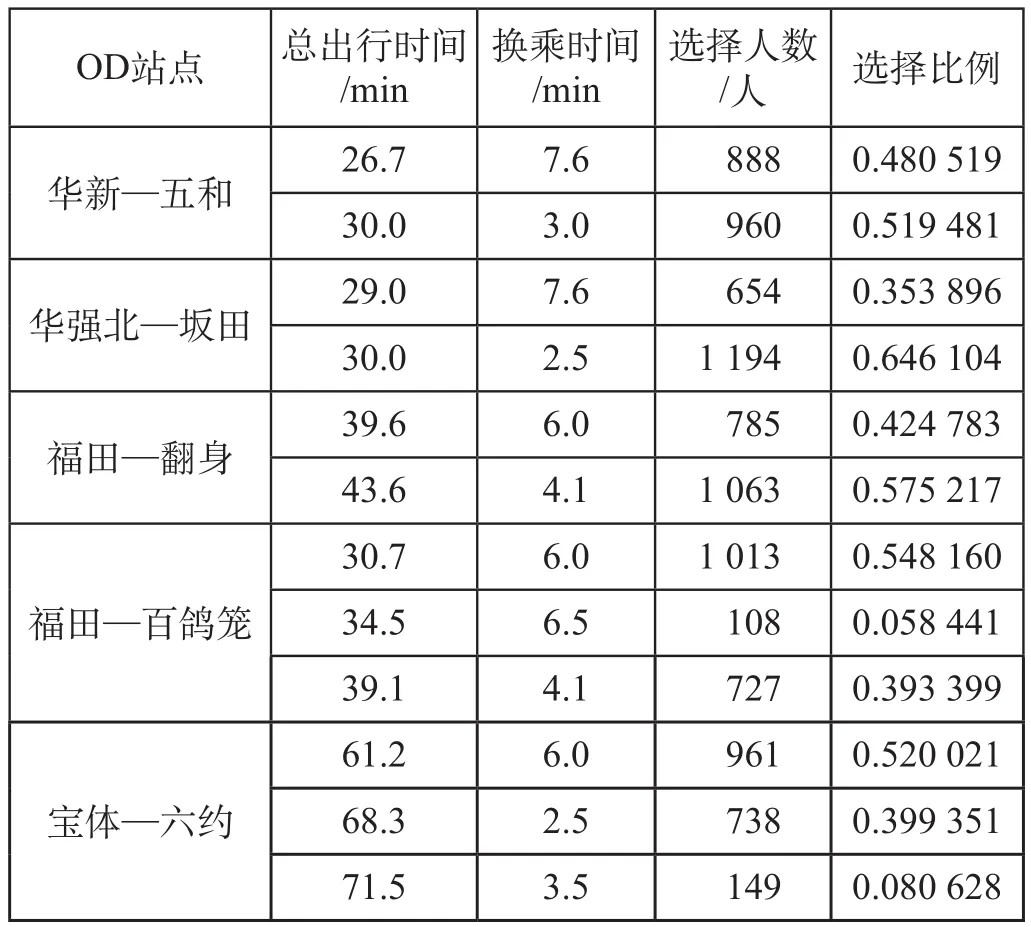
表 1 不同出行距离和出行时段条件下旅客路径选择参数值表

表 2 正态分布参数表
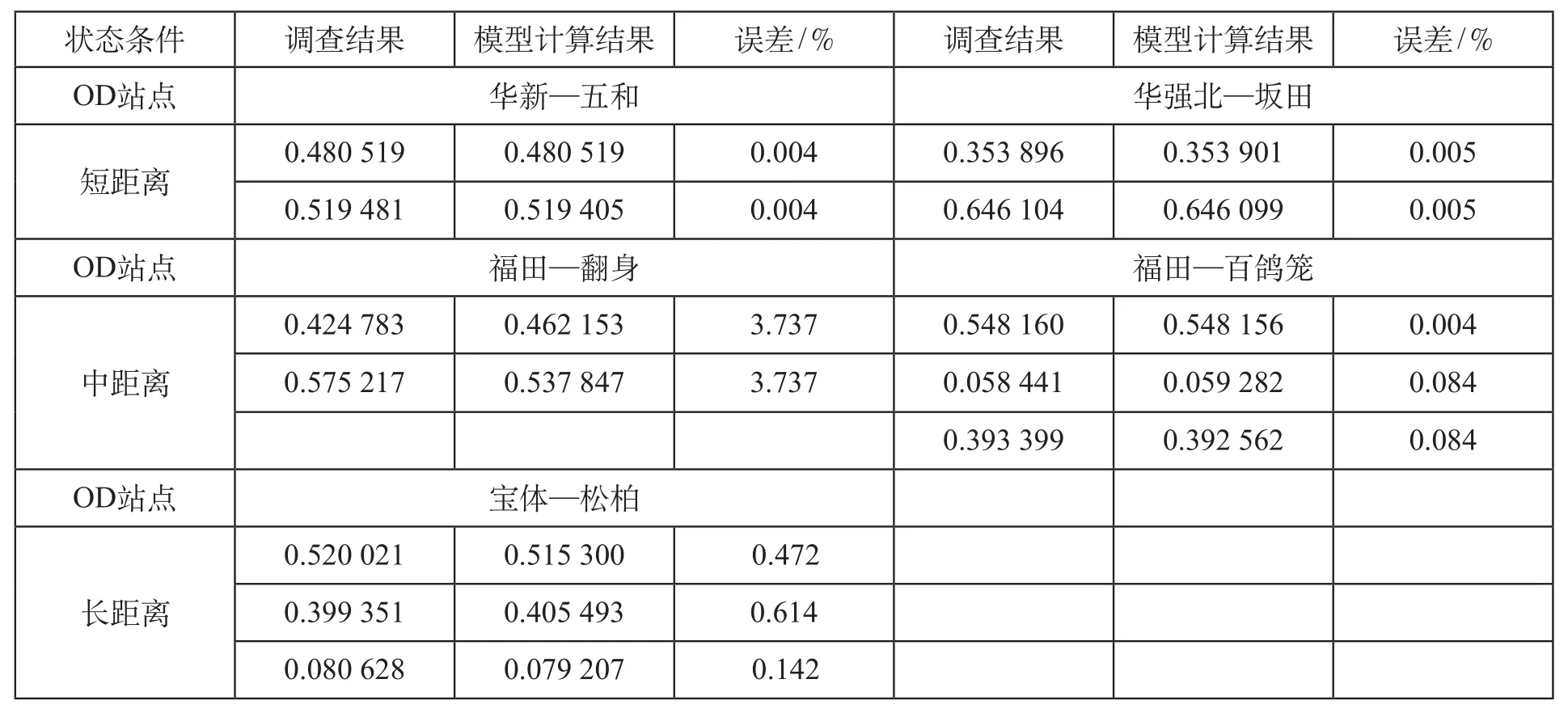
表 3 交通调查与正态分布概率模型预测计算对照分析表
从实际交通调查结果与正态分布模型预测计算的对照分析表可以看出,在 OD 站点中,计算结果与调查结果偏差最大的是华强北—坂田,误差为 3.737%;偏差最小的是华新—五和,误差为0.004%。总体来看,误差率不大于 4%,说明模型测算得到的路径分担比例与实际的拟合度达到96%,符合实际应用需求。
4.3 模型参数分析
深圳地铁多路径选择模型采用的是正态分布概率模型,在算法中 α、μ、σ 的变化直接影响选择结果,通过对典型 OD 对分析比照,对有关因素进行了灵敏度分析,旨在准确把握当某些影响因素发生变化时,各家运营商的清分比例变化情况。
根据调研数据和模型计算表明,当 α 的取值越来越大时,换乘时间长的有效路径的分配比例将会下降;反之,分配比例将会上升。当 μ 的取值越来越大时,出行时间越长的有效路径的分配比例将会下降;反之,分配比例将会上升。当 σ 的取值越来越大时,分配比例越大的有效路径的分配比例将会下降;反之,分配比例将会上升。
5 结束语
各个有效路径的旅客分担比例是地铁公司进行清分票款的主要依据,通过模型算法开发出一套切实有效的多路径比例计算软件,并投入实际应用。如何继续改进模型算法,使之能适用于更多的城市轨道交通系统,并能更准确地计算城市的有效路径分担比例,为地铁公司清分系统提供确实有效的基础数据是值得深入研究的方向。
