加权残差平方和最小的组合预测组合权重的确定

殷春武

（西京学院，西安710123）

自J.M.Bates和C.W.J.Granger在上世纪60年代证明了2种或2种以上无偏的单项预测可以组合出优于每个单项的预测结果,即组合预测方法能克服单个预测模型的局限性，集结更多的有用信息并有效地提高预测的精度后，组合预测逐渐成为专家和学者研究中运用的主要方法【1-3】。组合预测的主要思想是将各种单一预测模型通过加权集结从而得到最终的预测结果，在组合预测模型的研究中，现在主要的研究方向是如何来确定各单个预测模型的权重【2】。

关于单个预测模型的权重的研究经过各学者的研究，已经有了一定的研究成果，基于不同的考虑得到不同的加权系数的权重确定模型，并在实际应用中得到了较好的运用。但是通观现有组合预测研究可以发现，在确定各单个预测模型的权重的时候并没有考虑到历史数据的新旧程度对建立模型的影响。即对于某一社会经济问题，由于受到市场环境、社会环境及国家宏观调控政策等方面的影响，近期的数据对于最终的预测结果的影响程度肯定要比远期的数据的影响程度要大，所以在对后期数据的预测建模过程中，应该对于所采集的历史数据的不同时期给与不同的权重，这样建立的组合预测模型更符合实际情况，且预测模型的实用性和精度会进一步提高。

本文将充分考虑新旧历史数据对模型精度的影响程度的不同，给出一种加权残差平方和最小的最合预测模型组合权重确定模型，并基于离散情况下，给出组合权重确定模型。

1 基于时间权重的组合预测模型组合权重确定模型的建立

针对某一预测问题，采集到历史数据为X=(x(1),…,x(n))T，设预测对象存在m个单项预测方法，利用这m个单项预测方法得到的第i个单项预测方法的预测值为fi,i=1,2,…,m。组合预测的基本形式为

其中，w1,w2,…,wm为各种预测方法的加权系数。第i个单项预测方法第t时刻的预测值为fi(t)(i=1,2,…,m)。

1.1 组合加权系数恒大于零的不合理性分析

在现有学者关于组合预测权重确定模型中，一般都事先假设加权系数满足条件其实这是不合理的，假设第t时刻的历史数据值为x(t)，而采用m种单项预测方法后，第t时刻的模拟值为fi(t)，如果每一种单项预测方法的模拟值都满足fi(t)≥x(t)，且加权系数满足，则组合模拟值

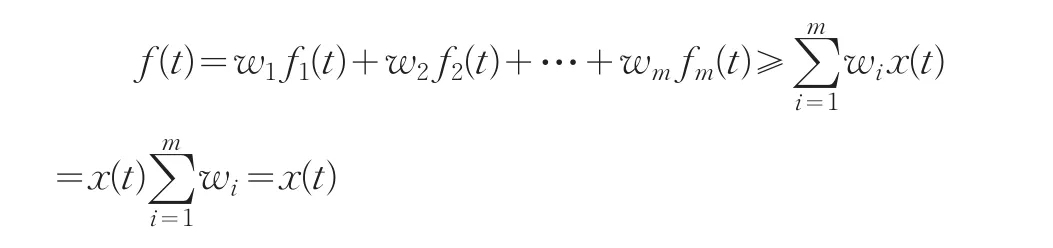
即f(t)≥x(t)，此式表明将单一预测方法的模拟值进行加权组合后的组合预测值肯定是不小于原来的建模数据，这与实际生活中要求组合预测值和建模数据相等是不符的。而要使得组合模拟值和建模数据相等，只能是要求加权系数可正可负。

定理1组合预测模型的组合加权权重可正可负。

1.2 时间权重的探讨

在利用历史数据建模的过程中，一般离建模时间越近的历史数据对后期的预测结果影响程度越大，离建模时间越远的历史数据对建模结果的影响程度越小，故在建模的时候应该考虑时间的时效性，为了能反映出历史数据的新旧程度对建模结果的影响程度，可以根据历史数据的时间先后顺序对各时间段的历史数据赋予一定的权重，即时间权重，下面给出其定义。

定义1 设ρ（t）为第t时期的历史数据对模型精度的影响程度的权重，则称ρ（t）为时间权重。

时间权重函数ρ（t）主要是反映第t时期的历史数据的对预测模型精度的影响程度，则时间权重应该是一个正数。考虑到在建模过程中，虽然新旧数据对建模结果影响程度上的差别存在，但是相邻两个数据的贡献程度差别不应该过大，即时间权重ρ（t）的增加也不能够增加过快，应该是一个比较平缓。其次，虽然随着t的推移，ρ（t）是逐渐增加的。但是当t无限增大的时候，最开始的历史数据和最后面的历史数据的贡献程度也不能相差太远，否则最开始的历史数据就可以忽略不计了，这与采集该历史数据进行建模的原理相违背。故当t无限增大的时候ρ（t）的取值也不能过于太大，综合考虑各方面的因素，时间权重函数ρ（t）应该满足条件：0＜ρ（t）＜1。

同时在时间权重的确定过程中，时间权重和组合预测的权重确定是相互有联系的，应该组合权重同时确定。同时在确定组合预测模型的权重向量w=(w1,w2,…,wm)的过程中，考虑到最后预测的值应该和实际采集到的数据的残差δt=f(t)-x(t)的平方和尽可能的小，为此，在考虑历史数据新旧程度不同对模型精度影响程度大小不同的情况下，建立如下加权残差平方和最小的组合预测权重确定模型

在时间权重ρ（t）给定后，通过极值的原理可以计算出组合权重的计算公式。

2 模型的求解

基于时间权重的加权残差平方和最小的组合预测权重确定模型给定后，下面运用极值最小的方法来确定该组合权重。对目标函数关于变量wk,(k=1,2,…,m)求导，并令其导数等于零，则得到如公式

为便于计算，将上面的式子写成矩阵的形式，则有

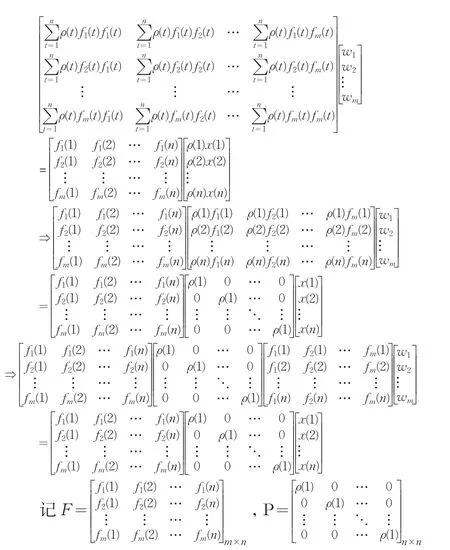
X=(x(1)x(2)…x(n))T,W=(w1,w2,…,wm)T

则上面的矩阵可以表示成FPFTW=FPX从而得到最终的基于时间权重的组合加权权重计算公式为

W=(FPFT)-1FPX

定理2基于时间权重向量ρ（t）的残差加权平方和组合预测加权权重为

W=(FPFT)-1FPX

3 结语

在以往的组合预测建模过程中，从未考虑到新的历史数据对预测模型的影响程度比成旧数据对预测模型的影响程度要大这个因素。本文充分考虑到时间因素对预测模型的影响，建立了带有时间权重的组合预测加权系数确定模型，该模型充分考虑了预测模型建模过程中历史数据的时效性。同时，确定时间权重时，在充分分析实际需求的前提下给出了时间权重函数应该满足的条件，并基于其所满足的条件给出了一个时间权重函数。通过实例计算分析发现，运用本文所给的模型所得的组合预测方法能有效提高预测精度。

[1] Tang Xiaowo,Zhou Zongfang,Shi Y.The Error Bounds of Combined Forecasting[J].Mathematical and Computer Modelling,2002,36(9).

[2] 陈华友.基于相关系数的优性组合预测模型研究[J].系统工程学报,2006,21(4).

[3] 陈华友,赵佳宝，刘春林.基于灰色关联度的组合预测模型的性质[J].东南大学学报，2004,34(1).