基于遗传算法的舰载机对海导弹攻击任务分配模型研究

夏惠诚，申战胜，伊柏栋

(海军大连舰艇学院，辽宁 大连 116018)

基于遗传算法的舰载机对海导弹攻击任务分配模型研究

夏惠诚，申战胜，伊柏栋

(海军大连舰艇学院，辽宁 大连 116018)

基于远程目标指示的对海导弹攻击是未来舰载机对海作战的主要样式。根据舰载机对海作战的实际情况，本文以对敌毁伤效果、舰载机损失和耗弹量3个指标作为目标函数，构建了多目标决策模型，并运用遗传算法对模型进行优化解算，验证了模型的合理性和实用性。

舰载机;远程目标指示;导弹攻击;多目标决策;遗传算法

0 引言

正确的作战行动要依靠正确的作战决心来指导，正确的作战决心要依靠正确的作战行动来实现。对于航母编队自身而言，舰载机对海导弹攻击任务分配的主要任务就是在兵力编成和海情判断的基础上，对舰载战斗机兵力进行合理分配，就是将敌实际来袭的各目标合理地分配给1个或几个舰载战斗机编队(或作战单元)来对敌实施拦截作战，从而达到较好的对海作战效果［1］。

1 舰载机对海导弹攻击任务分配模型的优化目标

基于远程目标指示的舰载机对海导弹攻击任务分配的根本目的是科学合理地使用舰载战斗机兵力，力求使编队对海作战的作战效能达到最大。因此，对海作战效果的大小是一个根本的评价目标。

“消灭敌人，保存自己”是一个根本的战斗准则，只有在消灭敌人的基础上，很好地保存己方兵力，才能更好地完成作战任务。航母舰载战斗机兵力十分有限，必须节省兵力资源，才能保证战斗的持续性。同时，现代作战条件下，航母编队面临的空、海威胁日益增大，并且敌来袭样式趋向小编队、多方向、多批次、空海立体的攻击，所以必须在完成作战任务的基础上，尽可能降低己方兵力的损失，才能保证整体的作战效果最佳，利于作战任务的达成。因此，舰载战斗机的损失情况也是舰载战斗机作战任务分配中需要考虑的一个目标［1－2］。

模型需要考虑的另外一个目标就是对海导弹攻击的耗弹情况，导弹的耗弹量最小，也就是意味着舰载机的出动数量最少，这也是“保存自己”的一个方面。

舰载机对海导弹攻击任务分配是一个多目标决策问题，各个目标是相互影响、相互制约的，必须综合考虑各目标对任务分配的影响，以舰载战斗机对海作战的根本任务和目的为依据，建立科学合理的任务分配模型。

2 目标函数的确定

舰载机对海导弹攻击任务分配的本质是实现舰载机突击编队内可用的导弹与目标之间的最佳匹配，以最少的作战兵力达到最大的毁伤效果。根据舰载机对海导弹攻击作战的兵力分配需要，确定了对敌毁伤效果、舰载机损失、耗弹量3个优化基本目标［1－3］。

2.1 对敌毁伤效果最大

对敌毁伤效果最大是舰载机对海导弹攻击任务分配模型的一个最主要目标，其基本问题可描述为：

我方基本情况——进行对海导弹攻击作战的舰载机数量有m架，其中第i架飞机(i=1，2，…，m)可携带空舰导弹Ri枚;敌方基本情况——敌编队共有n艘舰艇组成［3－4］。设第i架飞机对第j艘舰艇发射导弹xij枚，则舰载机的任务分配矩阵可表示为

在不考虑导弹的选择性和敌方抗击条件下，空舰导弹的单发命中概率为Pij，Pij体现了导弹固有的技术性能指标;第i架飞机重伤第j艘舰艇平均必须命中的导弹数为ωij，ωij是表征导弹战斗部威力及目标易损性的一个重要参数，它的值由导弹的威力和目标的易损性等技术特性共同确定;在此情况下，单发空舰导弹的毁伤概率为Pij/ωij，第i架飞机对第j艘舰艇的毁伤概率Wij可通过下式计算：

所有飞机对第j艘舰艇的总毁伤概率为

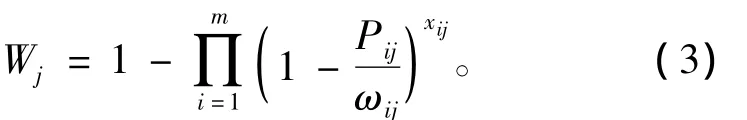
对敌毁伤效果最大既是要求对整个目标编队的毁伤概率达到最大，也是要求使“加权”毁伤目标函数值最大。所谓“加权”，是要考虑到各个目标的不同威胁程度和不同战术价值的权值。用kj表示第j艘舰艇的相对价值系数，则总的毁伤概率最大化的目标函数为

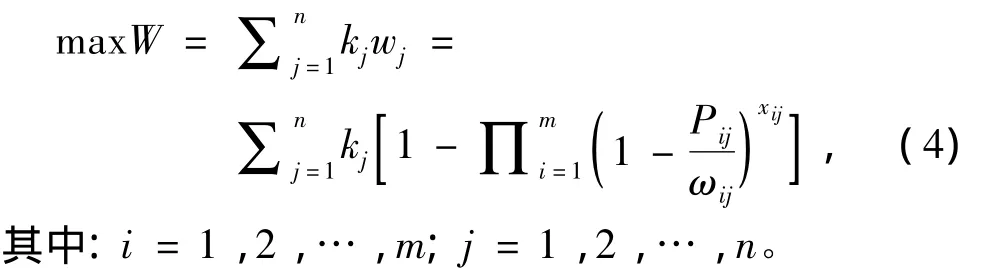
2.1.1 确定性因素对系数的修正

舰载机空舰导弹在对目标进行打击的过程中，其命中概率还会受到一些确定性因素的影响，例如在对目标编队中的指定目标进行打击时，对目标要求达到的毁伤等级以及目标的受损状态不同，都会对最终的导弹发射数量产生影响，因此需要对此类因素的影响进行修正［3］。

设βj为第j个目标的毁伤等级系数，通常取：

γj为第j个目标的受损状态系数，参考值为：

2.1.2 模糊因素对系数的修正

针对目标编队的综合防御能力，其“基本反导能力指数”与目标舰的探测设备、武器装备情况和战术技术性能直接相关，且基于可获得的数据能计算得出，但目标舰指挥员的指挥决策水平、人员素质及戒备程度等因素是无法确定的，具有很大的模糊性，在这里设第j个目标对第i架飞机的抗击系数为区间数，为简化计算，不考虑编队内其他舰艇对目标j的掩护和共同防御，或者说这一部分因素已经考虑在抗击系数中，则为考虑对方抗击条件下的导弹命中概率区间，因为目标的防御会降低导弹βjγjωij表示目标在不同受损状态下，为达到不同的毁伤等级时的导弹平均命中数。显然，βjγjωij≥1。若经计算 βjγjωij＜ 1 时，应取 βjγjωij=1。经过系数修正后总的毁伤概率最优化的目标函数可表示为的命中概率，因此，数学期望的取值区间为［0，1］。

很多情况下环境因素也会对导弹的命中概率产生影响，鉴于其模糊不确定性，可以用区间数表示这个系数。

2.1.3 人的因素对系数的修正

作为指挥者和决策者，指挥员的主观偏好和对兵力的战术运用可能决定一次军事行动的最终走向。这里用ρij表示指挥员的偏好系数，从某种意义上讲，偏好系数ρij可以看成是对目标抗击系数取值区间内的选择，或者说是对的明晰化，ρij反映了指挥员决定了兵力运用的方式后，第j个目标对第i架飞机的抗击系数。对的取值区间，指挥员可以根据其基本反导能力指数和战场态势而基本确定。偏好系数ρij反应了指挥员在特定的兵力运用条件下想要达到的效果，因此可以用普通的明晰数表示。同理，指挥员对环境影响因素的选择也可以用明晰数ξij表示。通过修正，总的毁伤概率最优化的目标函数可表示为［3－4］

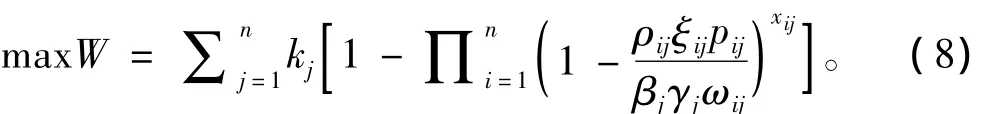
2.2 舰载机的损失最小

舰载机的损失主要考虑在对敌舰艇编队进行导弹攻击过程中，舰载机被敌空中和海上兵力击毁的情况，以对海导弹攻击作战中舰载机被敌击毁的损失值最小为目标，建立如下表达式：

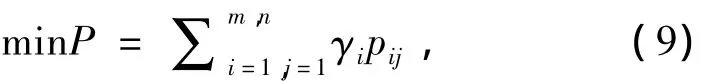
式中：γi为第i架舰载战斗机损失的权重;pij为第i架舰载战斗机对第j艘舰艇攻击时的平均被毁伤概率。

由于舰载战斗机型号不尽相同，且携带武器装备及驾驶人员不同，损失不同舰载机对编队战斗力影响大小也有所不同，所以在描述舰载战斗机损失这个目标函数时，应对不同舰载机赋予不同的权重系数 γi。

pij是综合考虑舰载战斗机的飞机性能、作战能力、突击位置等与编队战场感知能力、指挥引导能力、人员训练水平以及协同作战能力等因素相结合之后的定量值。

2.3 耗弹量最小

由于空舰导弹造价昂贵，航母携带武器数量有限，补给困难，且舰载机装卸复杂，故为了航母作战的延续性，减小作战的代价和风险，还应考虑空舰导弹的最小耗弹量问题。即以完成规定任务的最小耗弹量为最优目标，其函数表达式为

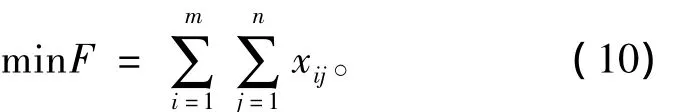
3 约束条件

约束条件是态势条件和决策条件等客观条件之间关系的反映。只有充分分析和考虑优化模型的约束条件，才能使优化模型具有实际意义。

3.1 兵力约束

1)可用舰载机总数量的约束

航母编队作战配置的舰载机数量有限，作战过程中又无法得到及时的补充。一般情况下，可执行对海导弹攻击作战任务的舰载机只占航母编队全部舰载机兵力的一半左右;同时，战斗出勤率等因素也对可用舰载机兵力产生较大的影响。因此，在制定舰载机对海导弹攻击任务分配方案时，必须考虑可用舰载机总数量这一约束条件，其数学表达式为

其中：N为舰载机对海导弹攻击作战中可用舰载机总数量。

2)空舰导弹数量约束

舰载机可挂载的武器类型和载弹量是有一定限制的，舰载机挂载武器必须符合实际情况。因此必须考虑舰载机可用空舰导弹数量的约束，数学表达式为

式(12)表示第i架舰载机发射的空舰导弹数量不超过其携带的空舰导弹数量。xij≥0则表示导弹数量的非负约束，且导弹数量xij应当取非负整数。

3.2 任务指标约束

上级的作战意图和作战任务要求，是制定舰载战斗机任务分配方案的根本依据和指导原则，对作战行动的优化必须以此为基础进行，并且任务要求是始终贯穿于作战行动优化过程中的，对任务分配方案的优化起到很大的约束作用。通常，所依据的任务指标约束包括以下2个方面。

1)对目标攻击效果的约束

针对不同舰艇、不同方向的敌突击目标，指挥员可能会提出一定的任务要求。指挥员所依据的任务指标，通常是下面这些中的一个或几个：

①使单个目标或编队中指定目标的平均命中导弹数(数学期望)达到毁伤等级(击沉、重伤、轻伤等)要求;

②使目标的命中概率达到给定值;

③使目标编队中指定的1个目标的命中概率达到给定值;

④使目标编队中指定的几个(或全部)目标的命中概率分别达到给定值;

⑤使编队中单个目标或指定目标被导弹按不同等级(击沉、重伤、轻伤等)毁伤的概率达到给定值。

以对某艘舰艇拦截效果的效益值作为指挥员提出的一个任务指标约束，数学表达式为

式(13)说明了对第j艘舰艇的攻击概率约束。其中：Wj为我舰载战斗机兵力对第j艘舰艇攻击效果的效益值;ωoj为指挥员要求的对第j艘舰艇的攻击效果。

2)我舰载机损失的约束

航母编队对海作战中舰载战斗机兵力的重要性和有限性，要求指挥员在任务分配方案制定中，必须考虑兵力的可能损失情况。因此，指挥员可能提出对攻击敌某艘舰艇的舰载战斗机兵力损失约束为

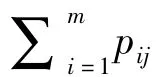
4 遗传算法仿真分析

上级通报：敌方1艘K级驱逐舰和3艘L级驱逐舰组成多用途型舰艇编队，企图以武力打破我方海上封锁。上级决定派遣舰载战斗机对敌编队进行远程目标指示下的导弹攻击，要求重伤敌全部目标;使各目标平均命中导弹数达到重伤等级要求;对K级驱逐舰的毁伤概率要求达到80%以上。计算使整个舰艇编队毁伤概率达到最大的分配方案［5－6］。

编队领受任务出海后，按上级要求在指定宽广海域对敌编队实施导弹攻击。气候、地形等环境因素对导弹发射和命中概率影响不大，可认为环境影响系数ξij=1;因为每个目标均处于完好状态，且对目标的毁伤等级要求为重伤，故毁伤等级系数βj和目标的受损状态系数γj均为1。

由于舰载机空舰导弹射程大于敌舰艇编队防空导弹的射程，且在远程目标指示条件下，舰载机通过战术数据链直接从编指或前置指挥所接收连续的目指信息，不对外进行目标的探测跟踪。所以，舰载机在远程目标指示条件下进行对海导弹攻击过程中，不会受到敌舰艇编队防空火力的威胁，舰载机由此造成的损失可以忽略不计。

通过以上分析，可建立简化的任务分配优化模型，如下式所示：

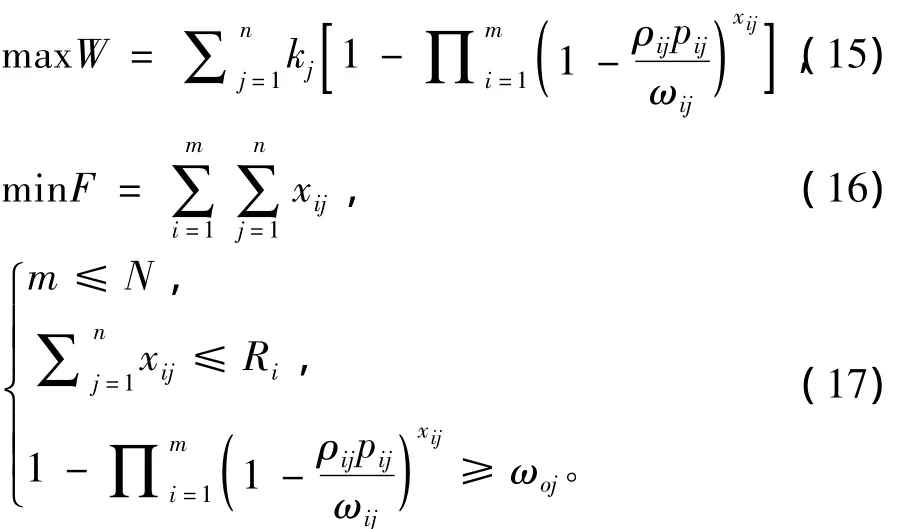
式中：xij≥ 0;i=1，2，…，m;j=1，2，…，n。

这里假设pij=0.8，Ri=2(即所有舰载机携带的空舰导弹数量均为2枚)。对于敌编队的1艘K级驱逐舰和3艘L级驱逐舰，经评估其相对价值系数为0.4，0.2，0.2，0.2;指挥员要求w01=0.8;其他各系数如表1所示。

?

针对上述模型，随机生成M(取值为100)个m×n阶的0－1矩阵，然后拉直，作为染色体，运用惩罚因子构造适应度函数(式(15)的权重值取为0.7，式(16)的权重值取为0.3，既相对于耗弹量来说，指挥员更侧重于进攻效果，追求更大的毁伤概率)，采用轮盘赌的选择方法，运用单点交叉和基本位变异，停止准则采用最大迭代数判断法，当遗传算法的迭代次数达到400代时，终止运算，输出结果。算法设计用 Matlab7.1语言编程实现，并在 Intel Core2 CPU1.86G的计算机平台上进行仿真计算。计算机运行结果如图 1 和图 2 所示［3，4，7］。程序终止时，最优的分配方案如表2所示。

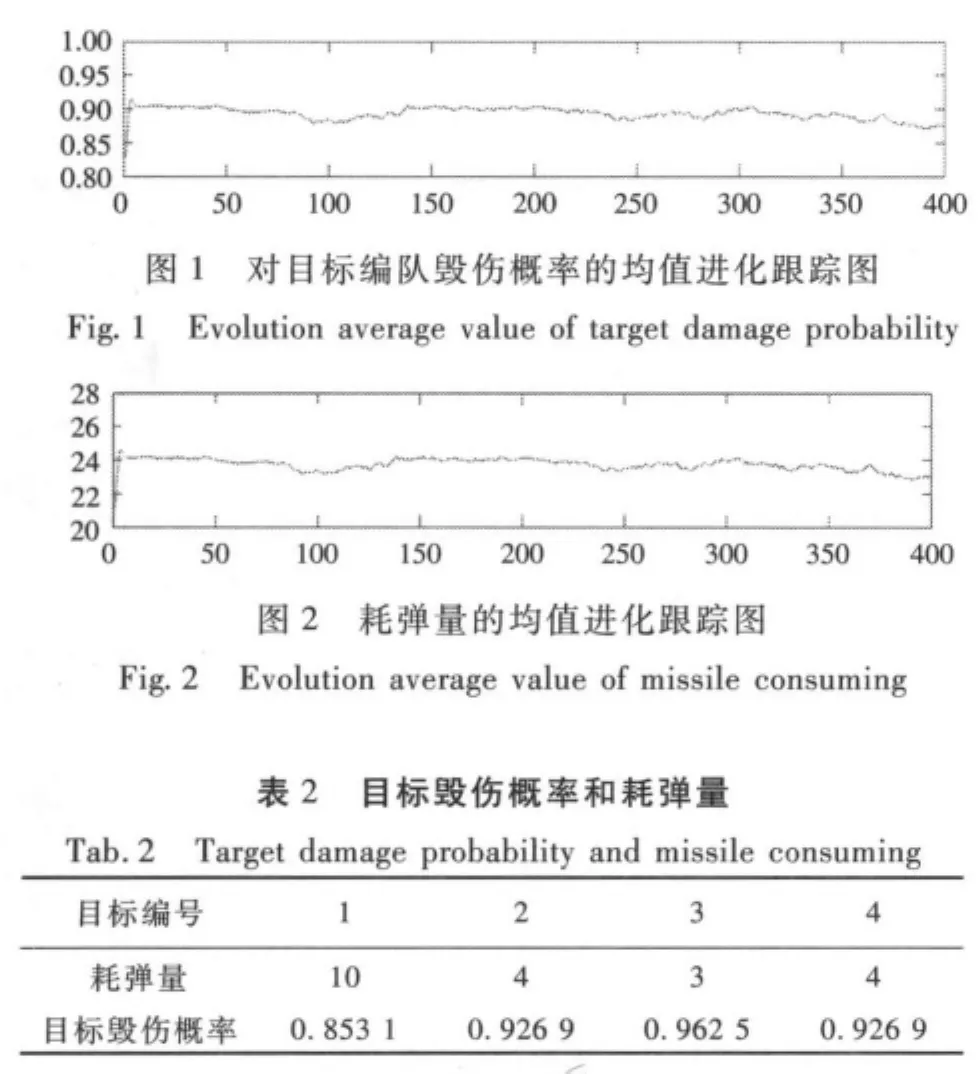
通过对仿真结果的分析可知，任务分配模型的结果符合论文优化的目的，既达到了作战要求，又确保了对整个舰艇编队毁伤概率达到最大，导弹消耗量达到最少。

5 结语

本文建立的任务分配模型，较好地解决了远程目标指示下舰载机对海导弹攻击的火力分配问题。在遗传算法求解模型的过程中，所提出的算法可以快速搜索解空间，获得最优解，验证了模型的合理性和实用性。

［1］孙庆生．大型编队对空防御中舰载机作战运用决策模型研究［D］．大连：海军大连舰艇学院，2010.43－44．

［2］王剑峰，等．美军航母舰载机反舰作战战术流程初探［J］．外军军事学术，2006，(10)：13－14．

［3］候志鑫．舰艇编队对海导弹攻击方案模糊决策模型研究［D］．大连：海军大连舰艇学院，2008.32－36．

［4］董凯．基于Agent的舰艇编队对空防御目标分配方法研究［D］．大连：海军大连舰艇学院，2010.39－45．

［5］郭张龙，等．基于遗传算法的目标分配问题研究［J］．现代防御技术，2002，(6)：4－7．

［6］欧阳海波，等．基于毁伤下界的常规导弹火力分配方法研究［J］．战术导弹技术，2011，(5)：41－44．

［7］雷英杰，等．MATLAB遗传算法工具箱及应用［M］．西安：西安电子科技大学出版社，2005．

Research on the mission assignment model of missile attacking on the sea by carrier aircraft on genetic algorithms

XIA Hui-cheng，SHEN Zhan-sheng，YI Bai-dong
(Dalian Naval Academy，Dalian 116018，China)

The missile attacking on remote target indication is the great mode of carrier aircraft fighting on the sea in the future．This paper has found multi-objective decision model of target damage，carrier aircraft damage and missile wastage，and checked the reasonable and practical of the model by genetic algorithms．

carrier aircraft;remote target indication;missile attack;multi-objective decision;genetic algorithms

E926．392

A

1672－7649(2012)05－0117－05

10.3404/j.issn.1672－7649.2012.05.028

2012－03－02;

2012－03－20

夏惠诚(1957－)，男，教授，博士生导师，主要从事水面舰艇作战使用研究。