复杂环境下罗兰C/北斗组合导航系统GDOP仿真分析

佟海鹏，徐海刚，刘兆平

(海军兵种指挥学院，广东 广州 510430)

复杂环境下罗兰C/北斗组合导航系统GDOP仿真分析

佟海鹏，徐海刚，刘兆平

(海军兵种指挥学院，广东 广州 510430)

导航系统的定位精度是影响舰船航行的重要因素。罗兰C系统和北斗定位系统由于受到台链地理位置、定位方式等因素的影响分别存在着定位精度低、安全保密性差等缺点。罗兰C/北斗组合导航系统则较好地解决了上述问题。针对几何精度因子(GDOP)方面对比研究了罗兰C系统和北斗定位系统组合前后的定位误差，并进行仿真分析。结果表明，组合后弥补了北斗定位系统有源定位的不足，一定程度上改善了罗兰C定位精度，提高了有效定位范围。

罗兰C;北斗;组合导航;几何精度因子;定位误差

1 概述

北斗定位系统是我国自行研制的一种区域性卫星定位系统，旨在为我国本土及周边地区服务。因其采用有源定位方式，使得用户数量受限且容易暴露用户位置。罗兰C由于受到建台地理条件的限制，目前所建的台链在某些区域定位精度很低，甚至有不能定位的区域，不能完全满足舰船导航定位精度的要求。罗兰C/北斗组合导航系统的建立较好地解决了上述问题。

任何一种定位系统对不同位置的目标，其定位精度是不同的。这就意味着目标位置的定位误差与目标相对于定位站的几何关系是密切相关的。不同几何布局的定位站对同一个位置上的目标，其定位误差是不同的，因此需要研究定位误差与定位站几何布局之间的关系。同样，在定位站几何布局一定的条件下，了解这种定位系统对不同空间位置上目标的定位误差分布，对于有效地使用这种定位系统，精确地对目标进行定位和跟踪也是十分必要的。

航海上的定位误差，不论属于哪种导航系统，都只与2个因素有关，一是量测值的误差，二是量测物标与测者之间的几何位置对定位精度的影响。对于某一定位系统而言，量测值误差的大小基本上在某一范围内变化，并且可用均方误差表示，该值可从大量的观测数据中统计求出。因此，定位误差就只是量测物标几何配置的函数了。

下面以双星定位为例说明几何精度因子或误差几何放大系数GDOP是对几何布局的反映，如图1所示。

图1 相对几何分布和精度因子示意图Fig.1 The drawing of opposite geometric distribution and accuracy factor

图1中(a)、(b)两图中的测距误差相同，而在图(a)卫星与用户位置夹角近似直角，几何位置好;在图(b)卫星与用户位置夹角小得多，几何位置差，圆环段为测距误差的反映。2种情况的位置精度非常不同，显然，图(b)比图(a)的定位误差大，即图(b)比图(a)的几何精度因子大。

一般情况下，在GDOP＜5的区域，属于高精度区;在5＜GDOP＜10的区域，具有较好的定位精度;在GDOP＞10的区域，定位误差比较大甚至不能定位，属于低精度区。

由于组合系统并未对单一系统做任何改变，只是在接收机处略有改动，因此组合后的系统量测误差与单一系统量测误差分析基本相同，而由接收机产生的测量误差也在算法设计时相减后相互抵消，它的影响可忽略不计。以下内容只针对几何精度因子方面分析组合前后对定位误差的影响。

2 “北斗一号”定位系统GDOP分析

“北斗一号”定位系统定位解算在中心控制站完成，其误差关系方程式为：

式中，GDOP为位置几何精度因子或误差放大系数。

设σ =20 m，σH=10 m;卫星在空间的摄动量相对于卫星至用户的距离可忽略不计;采用空间直角坐标系，地球模型采用的是接近地球实际情况的椭球体。应用式(3)可计算“北斗一号”定位系统服务范围内各点的几何精度因子。对“北斗一号”定位系统组合前的仿真结果如图2～图4所示。

图4 “北斗一号”定位系统垂直方向误差放大系数图Fig.4 The error amplification coefficient drawing of Beidou system in perpendicular direction

从仿真结果可以看出，“北斗一号”定位系统的3项误差放大系数在1.6～6.0之间变化，并随纬度的减小而增大，尤其在低纬度地区几何精度因子明显增大。从图3和图4还可以看出，垂直误差系数的影响占了整体定位误差系数的主要部分，相对而言水平误差系数的影响就小了很多。在“北斗一号”定位系统覆盖范围内，定位精度均满足航行精度的要求，只在低纬度地区略显偏大。

3 “长河二号”系统GDOP分析

“长河二号”系统观测点的船位误差σr与岸台和船位间相对工作区位置有关，即：

式中：σr为船位误差(均方差);θ为船位线夹角，用锐角进行计算;ρ为相关系数;E1和E2为船位线误差(均方差)，分别为：

式中：σDT1和σDT2为观测时差的误差(均方差);α为观测点到主、副台之间的张角。

从舰位线梯度理论可以证明，台对的距离差舰位线，可用该台对张角的平分线表示。因此，2条船位线夹角θ与台对张角α1和α2的关系为

正负号根据台对配置而定。

若设：σDT1=σDT2=σDT，将有关参数代入船位误差公式并取相关系数为最大值，即ρ=1整理后得到：

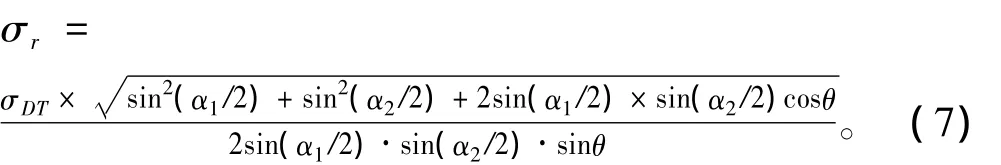
式(7)说明了观测时差的误差σDT与船位误差σ的关系。

若设时差精度σDT=1 μs，则式(7)船位误差公式即为时差的单位误差引起的船位误差，定义为定位几何精度因子，可表示为：

“长河二号”系统的定位误差与其几何定位因子GDOP有直接的关系，GDOP值大则定位误差大，反之亦然。因此可以用GDOP值为指标评估该系统在我国海区的定位误差。对“长河二号”系统3个台链的GDOP值进行仿真，其结果如图5～图7所示。

从上面的仿真结果可以看出，“长河二号”系统南海台链如图5所示，GDOP值随着经纬度的增大而增大，且在其覆盖范围内GDOP值普遍偏大;而东海、北海台链如图6和图7所示，则GDOP值随着经纬度的增大而减小，且也有相当一部分地区的GDOP值偏大(在GDOP均大于10，属于低精度区和定位盲区)。但不管3个台链GDOP值增大还是减小，该系统在北纬17°～22°，东经 119°～122°即台湾海峡的南部海区GDOP值都大于10，定位误差较大，甚至无法定位，因此“长河二号”系统在上述海区的定位误差较大，甚至无法正常使用。而该海域又恰是国家的重点战略区域。

图7 “长河二号”系统北海台链几何精度因子分布图Fig.7 The GDOP distribute drawing of Loran C system in Yellow Sea

4 罗兰C/北斗组合导航系统GDOP分析

4.1 罗兰C/北斗组合的工作原理及定位算法

北斗系统有2颗可用卫星，用户机测量距离2颗卫星的距离差可以获得1条双曲线位置线，而通过1个罗兰C导航台链也可获得1条双曲线位置线。这样可以将罗兰C时差与北斗时差相组合，2条双曲线位置线相交，交点即为用户机的位置。双曲线的定位方程是：

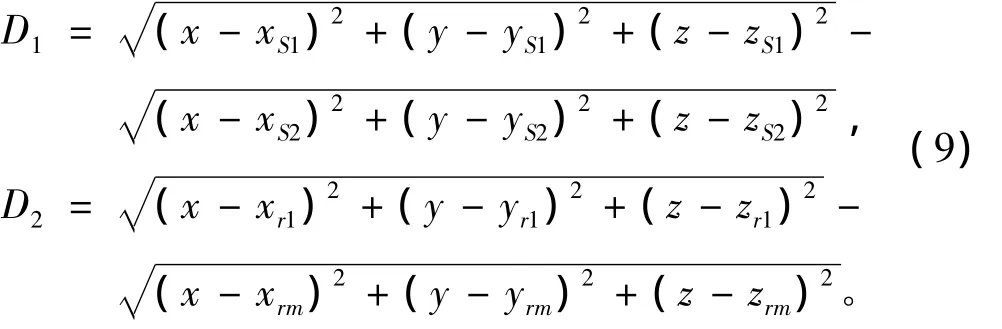
式中：(x，y，z)为用户的位置;(xS1，yS1，zS1)和(xS2，yS2，zS2)分别为卫星 S1和 S2的位置;(xr1，yr1，zr1)和(xrm，yrm，zrm)分别为罗兰C某副台与主台的位置;D1和D2为用户与卫星S1和S2以及罗兰C某副台主台的距离差。

为了导航方便，常采用大地坐标系，以地理坐标表示用户位置，因此可以利用大地坐标系与空间直角坐标系的关系，把式(9)转换到大地坐标系中，即：

其中，北斗系统采用的是北京－54大地坐标系，罗兰C采用的是WGS－72大地坐标系，由不同大地坐标系的换算将罗兰C的坐标系转换为北京－54坐标系中。

将式(10)在推算位置点按泰勒级数展开，并取一次项：

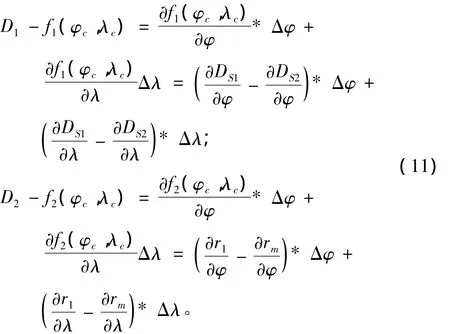
式中：DS1，DS2，r1，rm分别为推算位置到卫星S1和S2，罗兰C某副台与主台的距离;令：

其中：C1为观测卫星距离差与计算距离差的偏差;C2为观测罗兰C距离差与计算距离差的偏差。则有：

式(12)为二元一次方程，通过解方程可得到相应的Δφ和Δλ，从而得到对应的观测经纬度。

4.2 罗兰C/北斗组合导航系统GDOP分析

以下是对组合后系统几何精度因子的分析。将式(12)写成矩阵形式为

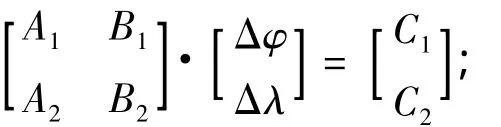
进一步简写可得：

定义通过罗兰C取得的距离差观测量C1的权为1，通过“北斗一号”定位系统测得的距离差观测量C2的权为

按定义协方差Cov(ΔX)=E(ΔX·ΔXT)可得：

假设2个距离差观测量C1和C2是相互独立的，其方差分别为σ1和σ2。

将式(16)两边同乘以地球半径的平方a2可得：

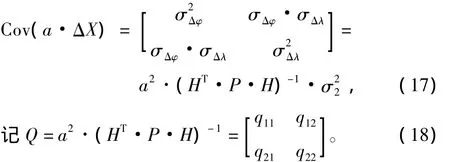
由此可见，几何精度因子表示最后定位误差是测距离差误差的多少倍，反映接收机、卫星及罗兰C台链之间相对几何关系对定位误差的影响。

图8为组合后定位系统的几何精度因子(GDOP)的仿真结果，其中设“长河二号”系统测距离差误差为100 m(0.3 μs)，“北斗一号”定位系统测距离误差为20 m。

从仿真结果可以看出，组合后系统的GDOP值在1.0～9.9之间变化，并且总体上随着纬度的减小而增大，定位精度明显优于单独使用“长河二号”系统，并有效地改善了单独使用“长河二号”系统时定位精度低，甚至无法定位的状况。

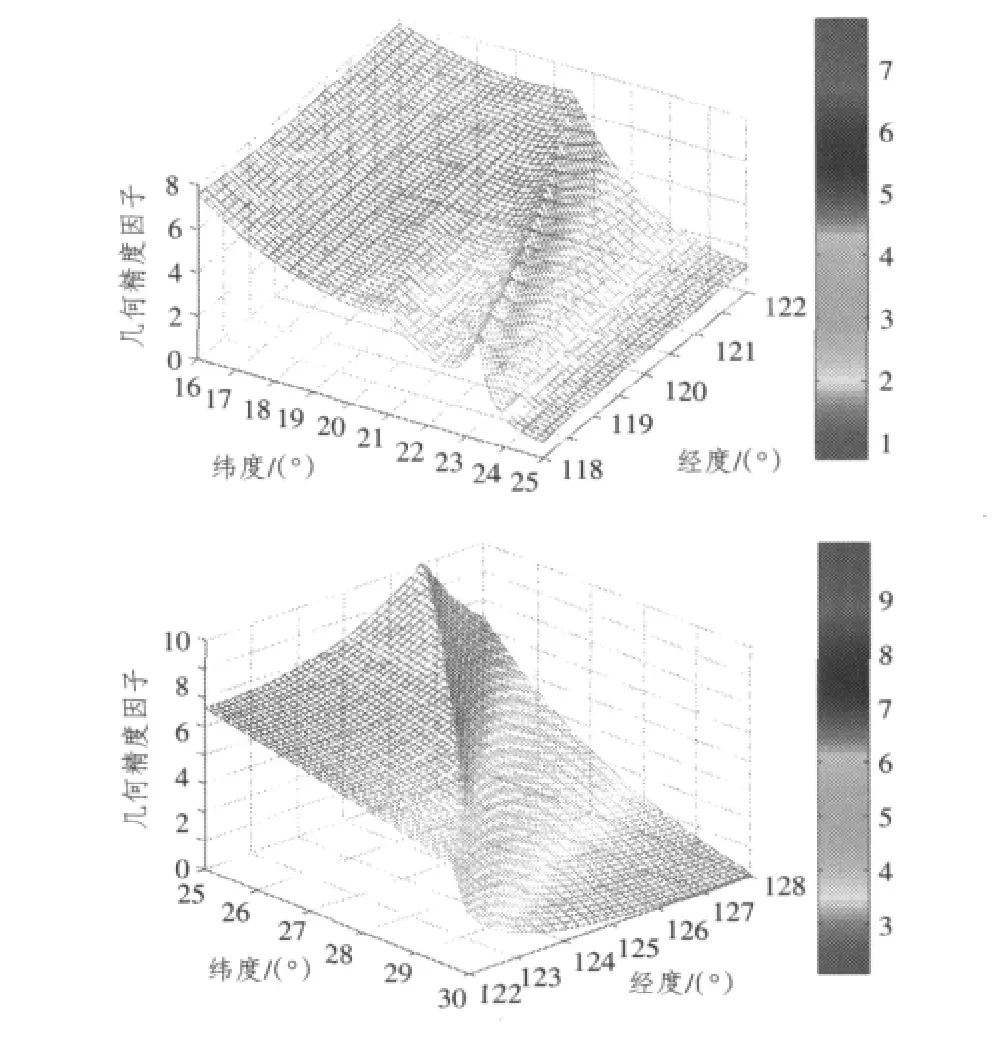
图8 组合后系统在其覆盖范围内几何精度因子分布Fig.8 The GDOP distribute drawing of integrated navigation system in effective range

5 结语

由于组合系统的定位测量误差是以“长河二号”系统的定位测量误差为基准(100 m，0.3 μs)，从总的定位效果来看，要低于单独使用“北斗一号”定位系统的定位精度，但降低的定位精度并不影响舰艇的航行安全。组合后系统实现了“北斗一号”定位系统的无源定位，同时又提高了使用“长河二号”系统的定位精度，因此组合后系统的综合效能大大提高，满足了现代舰船航行的多样化需求，具有重要的现实意义。

［1］SCHMIDT U．Autonomous star tracker based on active pixel sensors［A］．5th International Conference on Space Optics，ESA SP －554，Toulouse，France，2004：355 －358．

［2］LIEBE C C，ALKALAI L，DOMINGO G．Micro APS based star tracker［A］．Aerospace Conference Proceedings［C］，IEEE 2002：5－2285－5－2299．

［3］林雪原，何友．GPS/罗兰 －CISINS/AHRS组合导航系统及试验［J］．电子科技大学学报，2008，37(1)：4－7．

LIN Xue-yuan，HE You ．GPS/Luo's orchid-CISINS/AHRS combine navigation system and test［J］．The Journal of Electron Science and Technology University，2008，37：(1)4－7．

［4］周坤芳．现代舰船导航技术［M］．海军广州舰艇学院，2003．

［5］杨春钧．载波相位差分GPS/惯性组合导航［J］．南京航空航天大学学报，2000，32(1)：25 －30．

YANG Chun-jun．The carrier phase shift deci GPS/the inertia assemble navigate［J］．The Journal of Nanking Navigation Aerospace University，2000，32：(1)25 －30．

［6］汤磊，杨春金．基于Mapinfo电子海图和AIS的船舶导航系统的研究与实现［J］．通讯和计算机，2007，27(2)：72 －74．

TANG Lei，YANG Chun-jin．According to the search and realize of the ship navigation system of the Mapinfo electron natutical chartand AIS［J］．Telecommunication and Calculator，2007，27：(2)72 －74．

［7］OSTROM R M，SINGH M．Micromaching Techniques of Inertial Sensors［A］∥Proceedings of the National Technical Meeting“Navigation 2000”，2000．

［8］ROELOF W H，van BEZOOIJEN．SIRTF autonomous star tracker［A］．Proc．of SPIE，2003，4850：108 －121．

［9］ALEXANDER C D．Design of a day/night star camera system［A］．Proc．of SPIE，1999，3779：47 －54．

［10］DIETZ K L，RAMSEY B D．Daytime aspect camera for balloon altitudes［J］．Optical Engineering，2002，41(10)：2641－2651．

Emulational analysis for the GDOP of Loran C/Beidou integrated navigation system in complex environment

TONG Hai-peng，XU Hai-gang，LIU Zhao-ping
(Naval Arms Command Academy，Guangzhou 510430，China)

The positioning precision of navigation system plays an important role in shipping．For the limitation of stations place and positioning mode，there are different problems such as low positioning precision and unsafe quality in Loran C and Beidou．Loran C/Beidou integrated navigation system can settle above problems．In the paper，the positioning errors of Loran C，Beidou and Loran C/Beidou integrated navigation were researched in allusion to GDOP contrastively．The simulation of GDOP was presented．The conclusion indicate：the positioning precision and useable extension of Loran C were improved and the shortage of active Beidou position system was made up after integrated．

Loran C;Beidou satellite;integrated navigation;geometric dilution of precision(GDOP);positioning error

U666．11

A

1672－7649(2012)05－0108－05

10.3404/j.issn.1672－7649.2012.05.026

2010－07－06;

2011－07－27

佟海鹏(1981－)，男，讲师，主要从事海军作战环境研究。