球面舱壁的弹性稳定性分析

黄 旎，夏 飞，胡刚义，钱 群，肖 伟

(中国舰船研究设计中心，湖北 武汉 430064)

球面舱壁的弹性稳定性分析

黄 旎，夏 飞，胡刚义，钱 群，肖 伟

(中国舰船研究设计中心，湖北 武汉 430064)

基于静力法求解结构临界荷载的基本原理，导出旋转壳在均匀外压下弹性稳定性问题的一阶控制微分方程组。借助齐次扩容技术和精细积分法，采用Riccati传递矩阵法对均匀外压下球面舱壁的弹性稳定性问题进行数值求解。同时分析了各个参数(球壳半径、球壳厚度、环壳半径、环壳厚度和锥壳半锥角)对球面舱壁临界压力的影响。计算结果表明，各个参数中仅球壳半径和球壳厚度对结构的临界压力和失稳波数起决定性作用。

球面舱壁;传递矩阵法;稳定性

0 引言

球壳由于其优越的承压能力，被广泛运用于压力容器的端部结构。然而，球壳在外压作用下容易丧失稳定性而发生屈曲。因此，稳定性是结构设计者必须考虑的因素之一。

球面舱壁在外压下弹性失稳问题的研究，可以追溯到20世纪初。Zolly以扁壳理论为基础，求出了球壳在外压作用下的临界压力，即所熟知的球壳经典理论临界压力［1］。文献［2］则从一般旋转壳的理论出发，采用李兹法求解了轴对称变形厚球壳的线性屈曲问题。Len Colgan等人同样摒弃了扁壳理论的简化假设，采用摄动法分析了轴对称变形深球壳的线性稳定性问题［3］。然而，不管是从一般的壳体理论出发，还是以扁壳理论为基础，研究的仅仅是单一的球壳结构。但是在耐压容器的端部结构中，球壳与主耐压体往往采用环壳过渡以降低接合的应力。因此，球面舱壁包括球壳扇形段和平滑连接的环壳嵌入件。

本文以与锥壳相连的球面舱壁为研究对象，从基于变形后的平衡微分方程出发，结合结构的几何方程和物理方程，建立关于各个位移和内力分量为未知状态向量的一阶偏微分方程组。对于未知状态向量，在周向利用三角函数展开分离后，结构的一阶偏微分方程组转化为一阶常微分方程组，建立起结构各个壳段的传递矩阵，然后利用齐次扩容和细积分技术对微分方程组进行数值求解，计算结构的临界压力值。计算中研究了球壳半径和厚度、环壳半径和厚度、锥壳半锥角对结构临界压力的影响，可为球面舱壁的结构稳定性设计提供参考。

1 旋转薄壳的基本方程

旋转壳上任一点坐标可用曲率坐标(s，θ)表示，s为经向方向的弧长，θ为圆周方向角度，相应的主曲率半径分别为R1和R2，则拉梅系数分别为A=1，B=r，如图1所示。

图1 旋转壳微元体Fig.1 The element revolutionary shell

设u，v，w分别为e1，e2和法向 en方向的位移分量。对于弹性薄壳，在曲率坐标系下，表征壳体中曲面的各个应变分量与位移分量之间的关系可表示为：

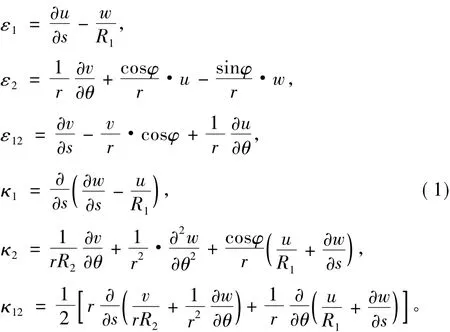
式中：ε1，ε2为中面沿e1，e2方向的薄膜应变分量;ε12为中面的面内剪应变;k1，k2和k12为弯曲应变分量。

在线弹性分析中，采用勒夫简化的物理模型，即结构的各个内力与应变的关系式为：

式中：T1，T2和T12为薄膜内力分量;M1，M2和M12为弯曲内力分量。

则微元体的平衡方程组为

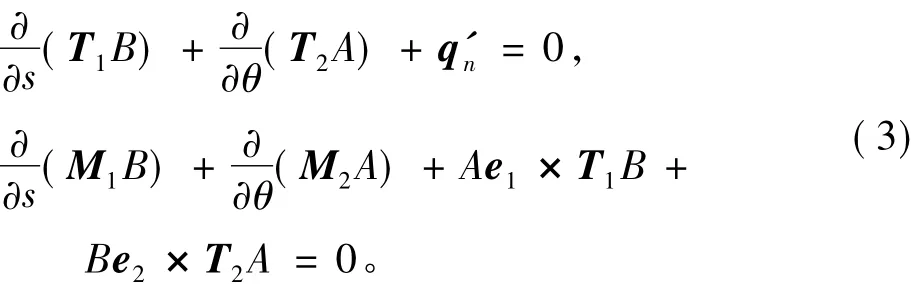
2 稳定性一阶微分方程的建立和传递矩阵的推导

研究薄壳稳定性问题的手段主要有静力法和能量法两大类。笔者采用静力法来研究球面舱壁的弹性稳定性问题。为计算结构的临界压力值，假设结构有2种不同的平衡状态。假设在失稳之前，整个结构在薄膜应力状态下保持稳定平衡，为状态Ⅰ;在微小的扰动荷载下结构随即失去薄膜应力状态下的平衡，重新建立起微小弯扭变形状态下的平衡，为状态Ⅱ。为研究状态Ⅱ的静力平衡是否稳定，平衡微分方程需建立在新的变形状态Ⅱ之下，即为上节的方程组(3)的各个展开式。由于状态Ⅱ是非常接近状态Ⅰ的平衡状态，因此状态Ⅱ下的各个内力TⅡ、内力矩MⅡ和位移UⅡ则可表示为状态Ⅰ下的内力TⅠ、内力矩MⅠ和位移UⅠ与相应的增量T，M，U的和，即

对向量{Ust}沿周向以三角函数分离变量［5］后，上式可改写为

式中：{Ust}m={um，vm，wm，T1m，Fvm，Fwm，M1m}，um，vm，wm，T1m，Fvm，Fwm，M1m为只与s有关的状态函数。为求出临界荷载值，假设给结构加一非常微小的挠动荷载。在该荷载作用下，分析状态向量{Ust}m的某一状态分量如法向位移wm。当该分量在压力P为P0时，w突然增大或减小，则P0为结构的临界荷载值。因此，式(4)将改写为

式(5)中的[A]m即为结构的传递矩阵，{P}为结构的微挠动荷载向量。球面舱壁是一种组合壳形式，将各个壳段的几何特性代入[A]m中，可得到球壳、环壳和锥壳的传递矩阵的具体表达形式，同时在各个壳段的连接处用点传递矩阵传递，并用齐次扩容精细积分技术对式(5)进行求解［6］。

3 算例分析和参数研究

3.1 算例分析

左端固支的与锥壳相连的球面舱壁结构示意图见图2。图中 R=1 000 mm，r=270 mm，L=781 mm，t=t1=7 mm，t2=10 mm，θ=82°。材料弹性模量E=2.0×105MPa，泊松比μ=0.3。

根据以上所述的传递矩阵法基本原理，采用Matlab编制与锥壳相连接的端部球面舱壁的稳定性计算程序。通过计算，结构的最小失稳临界压力Pcr=12.212 MPa，对应的环向失稳波数为14。最小临界压力下结构归一化后的法向位移沿母线方向弧长的形状如图3所示。

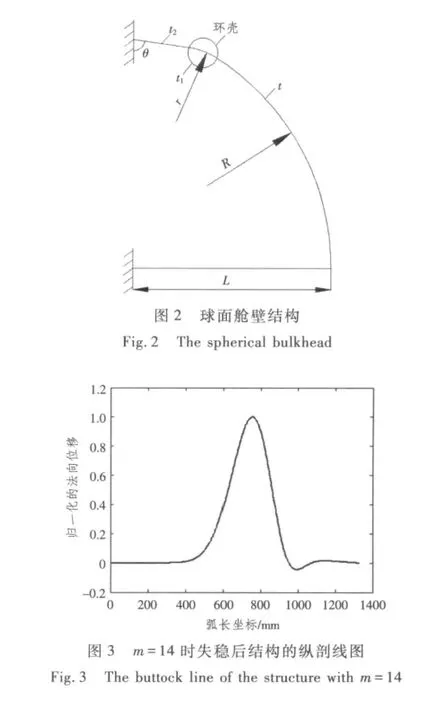
由图中可以看出，结构在球壳部分上失稳，因此可采用球壳经典理论临界压力计算公式进行验证。本算例中球壳部分的经典理论临界压力为11.86 MPa，二者误差为2.9%。为了进一步验证失稳波数的正确性，笔者采用Abaqus有限元软件对结构的弹性稳定性进行分析，对比结果如表1所示。从表中可以看到，2种方法计算得出的环向失稳波数相同，失稳临界压力值十分接近，相对误差不超过3%。

表1 失稳临界压力对比Tab.1 The comparison of the critical load

3.2 参数研究

在3.1节中基本结构的基础上，保持其他结构参数不变，只改变某个参数的大小，计算该参数在各个数值下结构的临界压力。本文研究了球壳半径、球壳厚度、环壳半径、环壳厚度和锥壳半锥角对结构临界压力的影响，各个参数数值的改变如表2所示。

表2 各个参数数值Tab.2 The value of a series of parameters

计算结果表明：结构首先在球壳上失稳，这说明球壳是整个结构中的薄弱部分;随着球壳半径R的增大，结构的最小临界压力Pcr随之减小，同时最小临界压力对应的失稳波数mcr也随之变小，如图4和表3所示;随着球壳厚度t的增加，结构的最小临界压力随之增大，对应的失稳波数mcr反而随之变小，如图5和表4所示;随着环壳厚度t1、环壳半径r和锥壳半锥角(π/2－θ)的增大，结构的最小临界压力有所增加，但增加的幅度很小，如图6～图8所示，且最小临界压力对应的失稳波数都不变，即mcr=14。

表3 不同球壳半径下的最小临界压力Pcr和失稳波数mcrTab.3 The minimum critical load Pcrand the buckling wave number mcrwith a series of radii of sphere shells

表4 不同球壳厚度下的最小临界压力Pcr和失稳波数mcrTab.4 The minimum critical load Pcrand the buckling wave number mcrwith a series of thicknesses of spherel shells

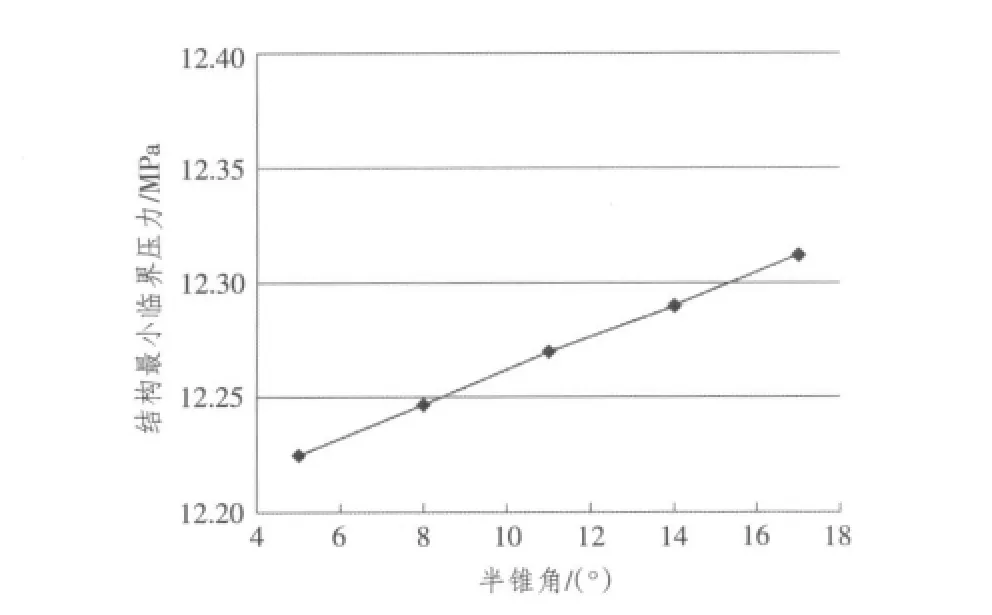
图8 不同锥壳半锥角下的最小临界压力Fig.8 The minimum critical load with a series of slopes of the cone shell

4 结语

通过以上分析，对于与锥壳相连接的球面舱壁结构，可以得到以下结论：

1)采用传递矩阵法计算该结构的弹性稳定性问题是可行的，且具有很高的精度。

2)在各个参数中，球壳半径及其厚度对结构的最小临界压力Pcr和失稳波数mcr起决定性作用。

3)当结构在球壳上失稳时，改变环壳厚度、环壳半径和锥壳半锥角对结构的最小临界压力Pcr和失稳波数mcr的影响不大。

4)参数研究结果验证了线性经典临界压力计算公式的准确性，对于整球壳、半球壳和不同高度的扁球壳均可采用经典公式确定其线性临界压力，而不必考虑边界条件对其的影响。

［1］徐秉汉，朱邦俊，欧阳吕伟，裴俊厚.现代潜艇结构强度的理论与试验［M］.北京：国防工业出版社，2007.249－252.

［2］VO KK，WANG C M，CHA Y H，et al.Buckling analysis of moderately thick rotational shells under uniform pressure using the ritz method［J］.Journal of Structural Engineering，2008，134(4)：594 －601.

［3］COLGAN L，HOWLETT P，THREDGOLD J.A perturbation analysis to solve the linearequations forsymmetric deformation of a deep spherical shell［J］.Mathematical and Computer Modelling，2009，49(5－6)：918－935.

［4］杨耀乾.薄壳理论［M］.北京：中国铁道出版社，1981.10－12.

［5］白雪飞，任文敏，郭日修.组合加肋旋转壳应力和稳定性分析的Riccati传递矩阵法［J］.工程力学，2008，25(3)：18－24.

BAI Xue－fei，REN Wen－min，GUO Ri－xiu.Stress and stability analysis of ring－stiffened joined revolutionary shell using riccati transfet matrix method［J］.Engineering Mechanics，2008，25(3)：18 －24.

［6］苏海东，黄玉盈.分析旋转薄壳的传递矩阵法［J］.工程力学，2008，25(9)：1－6.

SU Hai－dong，HUANG Yu－ying.A transfer－matrix method for analyzing revolutionary shells［J］. Engineering Mechanics，2008，25(9)：1－6.

Elastic buckling analysis of spherical bulkheads

HUANG Ni，XIA Fei，HU Gang－yi，QIAN Qun，XIAO Wei
(China Ship Development and Design Center，Wuhan 430064，China)

Based on the theory of calculating the critical load by means of statics method，one－order ordinary differential equations for the elastic buckling of revolutionary shells is derived.By means of the extended homogeneous capacity and high precision integration method，the elastic buckling solution of spherical bulkheads is obtained by using Riccati transfer matrix method.And the influence of the parameter(the radius of the spherical shell，the thickness of the sphere shell，the radius of the toroid shell，the thickness of the toroid shell，and the gradient of the cone shell)is examined.The calculated result show that the radius and the thickness of the sphere shell play a vital role in buckling analysis.

spherical bulkheads;transfer matrix method;stability

U663.4

A

1672－7649(2012)07－0035－05

10.3404/j.issn.1672－7649.2012.07.007

2011－11－29;

2012－05－16

黄旎(1984－)，女，博士研究生，研究方向为船舶结构设计与制造。