船舶喷水推进器进水流道效率的数值计算

王绍增，王永生，丁江明

(海军工程大学船舶与动力学院，湖北 武汉 430033)

船舶喷水推进器进水流道效率的数值计算

王绍增，王永生，丁江明

(海军工程大学船舶与动力学院，湖北 武汉 430033)

根据第21届、23届及24届ITTC关于喷水推进器能量公式的不同定义分别推导了进水流道效率的3种计算公式。在保持总流量不变的条件下，用满足最小偏差量的半椭圆来拟合进流面的形状，以CFD为工具对进水流道效率进行数值计算。对比分析7个不同进流面位置的计算结果，证明了进流面选在进口前1倍叶轮直径处是实用而合理的。研究结果表明，包含动能、压能、势能的进水流道效率公式最为合理，包含动能和压能的公式在CFD计算时可以作为流道效率的简化公式;重力对流道效率的计算值没有影响;由简化公式得到的计算方法可以大大减少计算量。

船舶;喷水推进;进水流道;数值计算;流道效率

0 引言

船舶喷水推进器主要由喷水推进泵、进水流道、喷口和转向倒车机构等部件组成。进水流道是喷水推进器的一个重要部件，其功能除了输送水流外还将船底来流的能量传递给装在尾板上的喷水推进泵。在进水流道里，来流能量的利用率直接影响着整个喷水推进器的效率。20世纪70年代以来，各国相继开展大量的喷水推进研究［1－3］，这些研究结果表明，性能优良的进水流道能大大提高喷水推进器的系统效率。因此，研究直接反映流道性能优劣的流道效率，对高性能喷水推进器的优化设计具有重要意义。

1 流道效率的定义及问题

进水流道的效率是衡量进水流道对来流能量利用程度的物理量。以第21届ITTC中喷水推进器内流体能量变化的定义图为标准(见图1)，其定义为流道出口面总能量与进流面总能量之比［4］：

式中：E1和E3分别为流道进流面和出口面的总能量。

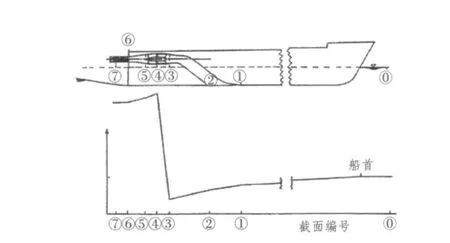
图1 喷水推进器内流体能量变化的定义图Fig.1 Definition of energy variety for waterjet

对于各截面上总能量的定义，3届ITTC中的能量公式不相同。在第21届、23届及24届ITTC喷水推进专家委员会最终报告和建议中分别为［5－7］：

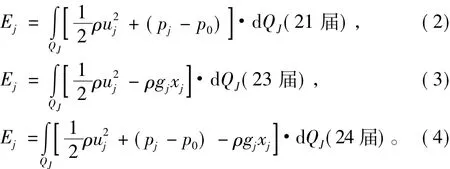
式中：j为截面的编号;Ej，uj，pj，xj和 gj分别为 j截面的总能量、速度、压强、距离势能参考面的高度及重力加速度;QJ为喷水推进泵的体积流量;ρ为流体密度;p0为环境压力。第21届能量公式中包括动能和压能，第23届中包括动能和势能，第24届中包括动能、压能、势能3项。把式(2)～式(4)分别代入式(1)，得到的效率公式有以下3种：

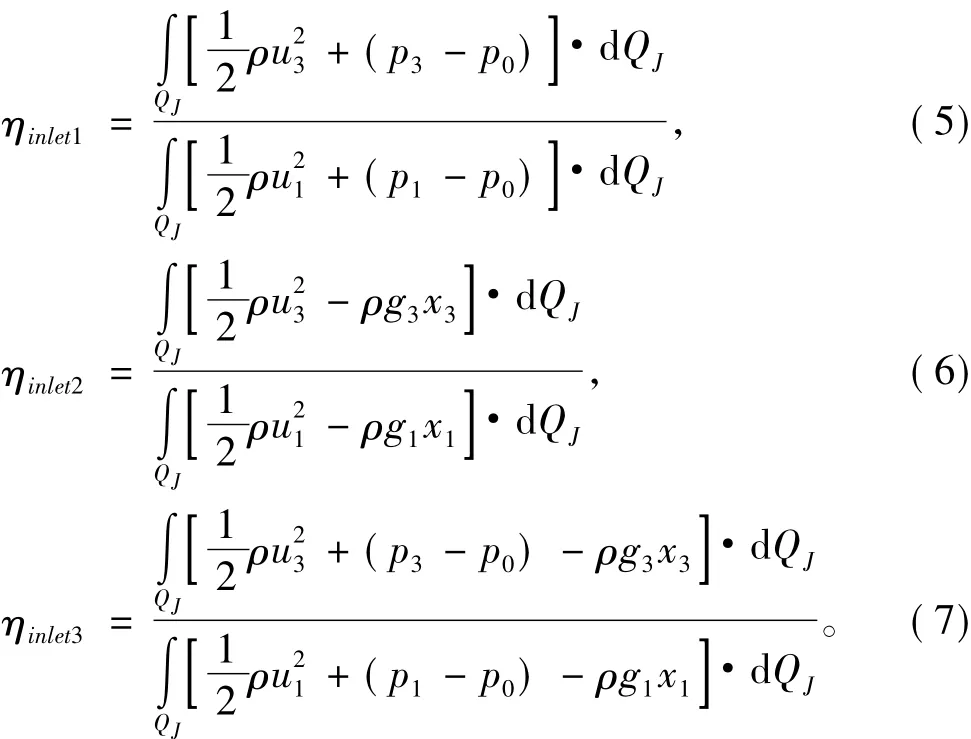
问题是用这3个效率公式计算的结果不相等。通过分析可知，动能在进水流道流动过程的总能量中占主导地位，无论是在流道进流面1的位置还是在流道出口3的位置动能均为主要成份，而对于压能和势能，考虑二者之一还是二者都要考虑是3个公式不相同的根本原因。本文基于以上问题，运用CFD方法，模拟进水流道的流场分布，分别计算出3种公式下的流道效率并进行比较，用数值实验的方法来检验哪一种公式是最合理的。

2 流道效率的数值计算

2.1 几何建模与网格划分

本文的模型选取了国外著名喷水推进器厂商MJP公司的叶轮直径为750 mm的某型进水流道(见图2)。计算域按文献［8］推荐取长、宽、深分别为30D，10D，8D(D为叶轮直径)。为保证计算精度，网格划分采用六面体结构化网格，近壁面采用O型网格并进行了加密，网格数为94万，y+控制在200以内。在流动变化剧烈区域，如唇部、弯管和流道与船底相交处进行了网格加密，第1层网格距壁面0.1 mm(见图3)。

2.2 控制方程与数值求解

利用基于中心节点控制和有限体积法的流体力学计算法求解RANS方程，选择SST k－ω模式对湍流进行模拟［9］。计算域上游进口设为速度进口，速度大小及梯度分布受航速及边界层的影响，边界层厚度按照公式 Prandt1 取 δ=0.37·x·(Re)－1/5，速度分布采用平板边界层速度分布表示［10］：

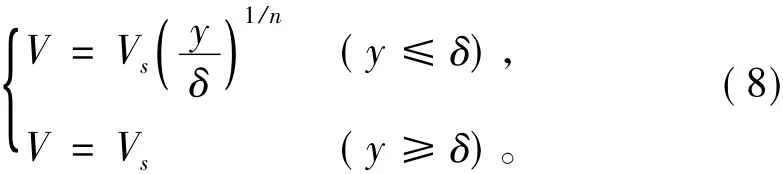
式中：V为边界层内流速;Vs为船航速;δ为船底边界层厚度;y为距船底的距离;指数n取为9。计算域设置竖直向下的重力，重力参考点选为无穷远处水面。下游的出流面设静压压力为相对压力0 Pa，即绝对压力为1 atm。流道出口设为流量出口，进水流道及船体设为无滑移壁面。

2.3 进流面位置和形状的确定

在求取流道效率时，难点在于精确求取进流面的位置和形状。图4为第24届ITTC中对喷水推进器水力模型控制体的定义。

图4 喷水推进器水力模型的控制体Fig.4 Control volume representing the hydrodynamic model of waterjet

控制体被定义为截面1A至截面6之间的流体体积。该体积一部分由喷水推进器实体的边界来定义，另一部分由实体进口A'D(见图3)前流动分界面BC来定义。这个分界面是在流动中的一个假想的面，表面上无质量穿越。

假想的进流面1A是在进口斜面切点(A')略微靠前位置。选择这个位置目的是避免由于进口的几何形状而带来的流动变形。点A'前面一个叶轮直径D的位置是较为常用和实用的选择。第24届ITTC中推荐半椭圆形进流面，长轴设为进口几何宽度的1.5倍。文献［11］的研究结果也说明进流面形状类似半椭圆(见图5)。

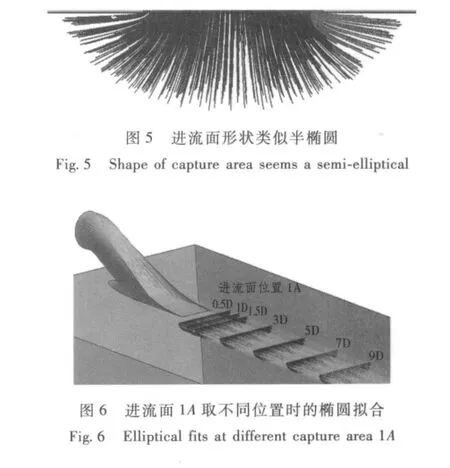
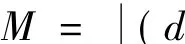
图7 进流面椭圆拟合的3种方案Fig.7 Three method of elliptical fits to capture area

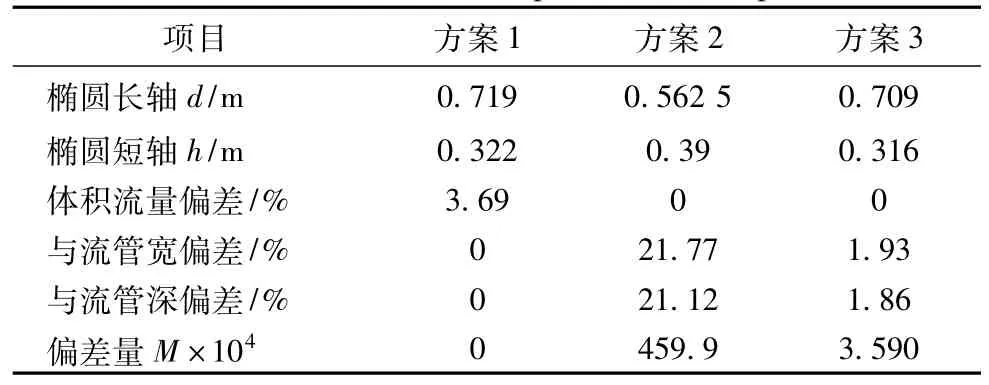
表1 进流面椭圆拟合的3种方案Tab．1 Three method of elliptical fits to capture area

2.4 流道效率的求取及结果分析

用求最小偏差量的方法拟合不同1A面位置时的进流面，在计重力的情况下按流道效率式(5)～式(7)分别求得效率的结果见表2。

表2 不同1A面位置时的流道效率Tab．2 Inlet efficiency at different capture area 1A

结果表明，随着进流面远离流道背部切点位置，流动损失逐渐加大，流道效率减小。因为进流面越靠近船首，计入控制体的船底流体流动时所扫过的面积就会越大，引起的摩擦损失就越多，而这部分摩擦损失不属于流道损失的范围，因此1A面的位置要尽量靠近切点。另一方面，当取0.5D时，椭圆有明显的减小趋势，说明已经发生流动变形。因此将1A面取在1倍叶轮直径处是比较合适的做法，文献［12］的计算也说明该位置较为合适。

为了分析动能、压能、势能在总能量中的分布，单独取1A面为1倍叶轮直径时的进流面和流道出口面的结果(见表3)。

表3 进流面1A和流道出口3处的能量分布Tab．3 Energy distribution at capture area 1A and outlet area 3

结合流道效率式(5)～式(7)和总能量分布规律分析可知：1)流动过程中，动能在总能量中占主导地位，动能逐渐转化为压能和势能;2)压能和势能在总能量中虽然所占比重较少，但是在计算过程中不能忽略，式(7)才是最合理的。

3 效率公式的分析及验证

上述结果证明了式(7)的合理性，然而在查阅大量文献后发现，在工程上，式(5)和式(6)的应用也十分广泛，不含重力势能项的式(5)常应用于水平管流，不含压能项的式(6)常应用于明渠流。问题应该回到对控制体的分析上——重力和压力在流动过程中对流体有何作用。

对于粘性、不可压、体积力只有重力的三维流动的控制方程仅为连续方程和N－S方程，在直角坐标系下的方程组为：

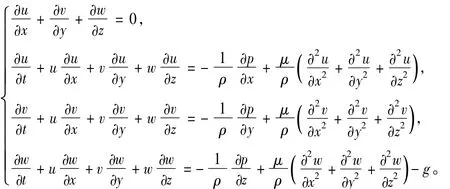
其中只有压强p和速度的3个分量u，v，w是未知量，4个方程4个未知量，方程封闭可以求解。在给定相同的初始条件和边界条件下，其解应当是确定的。不妨设P=p+ρgz，代入方程可得：

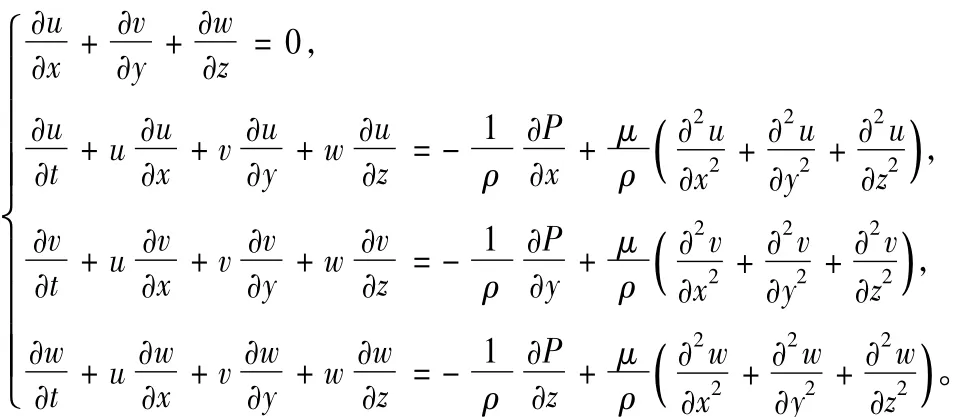
此方程组恰为无体积力时的控制方程，也就是说，不计重力计算所得的压强值P等于计重力时所得的压强值p再加上ρgz的值，即式(5)在不计重力情况下的计算结果等于式(7)在计重力时的计算结果。为进行验证，本文用第2部分的模型在不计重力的情况下重新进行计算，并用式(5)计算流道效率。选取进流面1A位于1倍叶轮直径处和流道出口面3处的结果与计重力时的计算结果对比如表4所示。

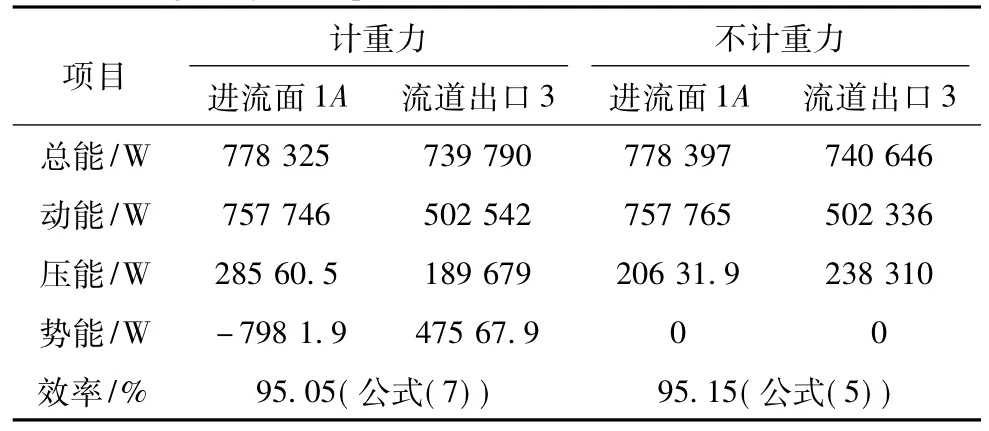
表4 计重力与不计重力时进流面1A处和出口面3处能量对比Tab．4 Energy's comparison between with gravity and without gravity at capture area 1A and outlet area 3

分析结果可知，以进流面1A的能量为例，计重力时压能与势能之和约为20.6 kW，不计重力时压能也约为20.6 kW，即在计算误差范围内二者是相等的。很明显，在出口面3处二者也是相等的。这证明了计重力时的压能与势能之和等于不计重力时的压能。因此求流道效率时可以直接用式(5)，前提是要在CFD预处理里不添加重力项，这将大大减少计算所需资源。也就是说，在CFD计算中，我们可以把式(5)看作是流道效率的简化公式。

根据以上结果，我们可以得到这样一种简化计算方法：即先在不计重力的情况下求解控制方程，然后再把所得压力值减去ρgz的值即得到实际的压力值。此结论适用于所有粘性、不可压及体积力只有重力的情况。这种简化计算方法在CFD计算中会节省大量的计算时间，因为如果流场中存在旋转域时必须要用瞬态计算，其花费的时间将是稳态的几倍甚至十几倍。

综上所述，式(5)适用于不计重力的情况，式(6)只适用于明渠流，式(7)适用于所有情况。

4 结语

3届ITTC的能量定义公式适用范围不同，其中包含动能、压能和重力势能3项的定义(4)是最全面的，适用于任何情况，而另2个公式的应用是有条件的。

计重力时与不计重力时的流道效率的理论值是相等的，通过数值实验分别计算的流道效率相差0.1%(可视为计算误差)，这与理论值的结论是一致的。数值实验的结果也证明了考虑重力与否不会引起流道效率的变化，这与流道效率的概念也是相符合的。

喷水推进器进水流道效率的计算公式为式(7)，也可以用简化式(5)(不在CFD预处理中添加重力项)进行计算，二者结果相同且后者可以有效地节约计算资源。

由于实尺度计算中重力场是必然存在的，我们可以先在不计重力的情况下求解控制方程，然后把所得压力值减去ρgz的值即得到实际的压力值。此结论可以推广到所有粘性、不可压及体积力只有重力的情况。这种简化计算方法可以大大减少CFD的计算量。

［1］ALLISON J L．Marine waterjet propulsion［J］．SNAME Transactions，1993，101：275 －335．

［2］刘承江，王永生，丁江明．喷水推进研究综述［J］．船舶工程，2006，28(4)：49－52．

LIU Cheng-jiang，WANG Yong-sheng，DING Jiang-ming．Overview ofstudy ofwaterjetpropulsion［J］．Ship Engineering，2006，28(4)：49－52．

［3］BULTEN N W H，VERBEEK R．Design of optimal inlet duct geometry based on vessel operational profile［C］．Proceedings of the Seventh International Conference on Fast Sea Transportation Conference．Ischia，Italy：University of Naples，2003.35 －40．

［4］KEEGAN DELANEY，MARTIN DONNELLY，et al．Use of RANS for waterjet analysis of a high-speed sealift concept vessel［C］．First International Symposium on Marine Propulsors．Trondheim，Norway：smp'09，2009．

［5］Final report and recommendations to the 21stITTC［C］．The 21stInternational Towing Tank Conference．Bergen and Trondheim，Norwegian：ITTC，1996.189－209．

［6］Report of thespecialist committee on validation of waterjet test procedures to the 23rdITTC［C］．The 23rdInternational Towing Tank Conference．Venice，Italy：ITTC，2002.387－711．

［7］Waterjet propulsive performance prediction-waterjet inlet duct，pump loop and waterjet system tests and extrapolation［C］．Final Recommendations of the Specialist Committee on Validation of Waterjet Test Procedures to the 24thITTC．Edinburgh，UK：ITTC，2005：7.5－02－05－03.2．

［8］刘承江，王永生，张志宏．喷水推进器数值模拟所需流场控制体的研究［J］．水动力学研究与进展，2008，23(5)：592－595．

LIU Cheng-jiang，WANG Yong-sheng，ZHANG Zhi-hong．Study on flow control volume in numerical simulation of waterjet propulsor［J］．Chinese Journal of Hydrodynamics，2008，23(5)：592－595．

［9］常书平，王永生，庞之洋，等．喷水推进流道格栅的流体作用力分析和强度计算［J］．舰船科学技术，2010，32(1)：110－114．

CHANG Shu-ping，WANG Yong-sheng，PANG Zhi-yang，etal．The hydrodynamicforceanalysisand strength calculation of waterjet intake grid［J］．Ship Science and Technology，2010，32(1)：110－114．

［10］张拯，王立祥．关于喷水推进装置平进口边界层影响系数估算的探讨［J］．船舶，2008，(3)：10－14．

ZHANG Zheng，WANG Li-xiang．Estimation for inlet boundary-layer affect coefficient around waterjet duct［J］．Ship ＆ Boat，2008，(3)：10 －14．

［11］于富强，丁江明，杨卫国，等．喷水推进器进水流道进流面形状研究［J］．舰船科学技术，2009，31(4)：54－57．

YU Fu-qiang，Ding Jiang-ming，YANG Wei-guo，et al．Research on stream tube and capture area of waterjet propulsion system［J］．Ship Science and Technology，2009，31(4)：54－57．

［12］DING Jiang-ming，WANG Yong-sheng．Research on flow loss of inlet duct of marine waterjets［J］．Journal of Shanghai Jiaotong University(Science)，2010，15(2)：158－162．

Numerical calculation of inlet duct efficiency of marine waterjet propulsion

WANG Shao-zeng，WANG Yong-sheng，DING Jiang-ming
(College of Naval Architecture and Marine Power，Naval University of Engineering，Wuhan 430033，China)

According to different energy definitions from the 21st，23rdand 24thITTC，three different kinds of inlet duct efficiency formulas are derived．On the consistent condition of total flow mass，the shape of capture area is fit by a semi-elliptical，and then inlet duct efficiency is calculated by CFD．Seven results on different locations of capture area are compared，which shows that it is practical and rational to choose capture area at one-impeller length before the inlet duct．The research result indicates that the formula including kinetic、pressure and potential energies is most reasonable，and the formula including kinetic and pressure energies can be used as the simplified efficiency formula in the calculation of CFD．The gravity has no effect on the value of inlet duct efficiency，and the amount of calculation can be greatly reduced by the simplified method derived from the simplified efficiency formula．

ship;waterjet propulsion;inlet duct;numerical calculation;inlet efficiency

U664.34

A

1672－7649(2012)07－0015－05

10.3404/j.issn.1672－7649.2012.07.003

2011－10－08;

2011－10－31

王绍增(1983－)，男，硕士研究生，研究方向为船舶喷水推进技术。