基于窗函数的FIR数字滤波器设计

CHEN Jing-song，LIU Yan-wei

0 引言

数字信息处理在现今的社会发展中已经起着非常重要的作用，而数字滤波作为数字信号处理的一个重要的组成部分，成为许多科学家研究的重点对象。根据单位取样响应h(n)的时域特性，现今的数字滤波器科学地被划分为两个形式的系统，一个是无限脉冲响应(IIR)系统，另外一个是限脉冲响应(FIR)系统。与IIR数字滤波器相比，FIR 数字滤波器有着严格的线性相位,且具有任意的幅度特性，使得传递函数没有极点，这在很大程度上保证了设计出的FIR 数字滤波器是平稳的。

找到一组数据（a,b），只要能满足特定FIR滤波器的要求就是设计的实质。而在完成设计滤波器设之后，还要进一步考虑将其实现的细节，像是选择哪一种结构的滤波器结构，滤波运算等。其中实现算法是实现FIR数字滤波器的一个重要实现部分，在本文中采用的窗函数的概念，就是对无限长的信号截取一段时间内的信号进程处理和分析，然后将得到的实验结果进行周期性的拓展，最终取得的无限进行进行傅里叶变换和分析，且通过与传统算法实现的FIR滤波器对比，用仿真实验说明本文算法的优越性。

1 窗函数设计及分析

窗函数w(t)本身具有频带无限的特征，即使是限制带宽的原信号x(t)，通过窗函数截断以后也具有了无限带宽的性质，使得频域的能量与分布得到了扩展。当然，在这个截断的过程中，即便采样频率很高，也会引起信号的一些误差。从一些实验数据中科学家们发现，这些误差都与窗函数频谱的两侧旁瓣有着非常紧密地联系，故针对不同的时域要采用不同的窗函数来进行截断，来确保与真实的频谱相接近。窗函数的种类相对来说资源比较丰富，本文就其中三种相对常用的窗函数性质和特点来简要地阐述一下：

1）矩形窗

矩形窗属于时间变量的零次幂窗，主瓣相对居中，旁瓣较高，有负旁瓣，容易在中带变化中带进高频干扰和泄漏，有负谱现象存着的可能。其矩形窗的时域和频域的表达式如下：

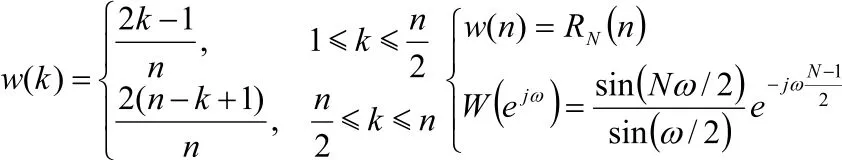
2）汉宁（Hanning）窗

3) 海明（Hamming）窗

海明窗也是余弦窗的一种，与汉宁窗相比，旁瓣达到了更小，且衰减速度相对较慢。海明窗函数的时域和频域的具体表达式如下：

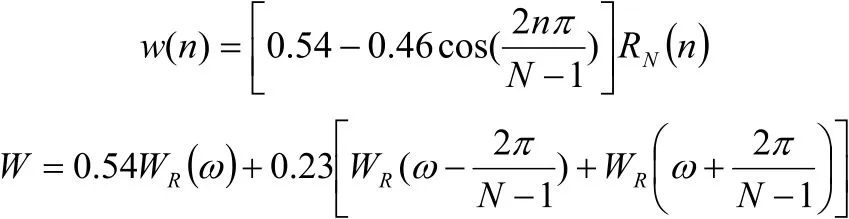
从上面的三个具体代表性的窗函数的描述上可以看出，不同的窗函数，对应的信号频谱影响不一样，导致的能量泄露也不一致，且这与傅里叶算法中产生的栅栏效应一样，都是不能完全删除的，故在进行窗函数的选择时，应考虑被分析信号的性质与处理要求。如果仅要求精确读出主瓣频率，而不考虑幅值精度，则可选用主瓣宽度比较窄而便于分辨的矩形窗，例如测量物体的自振频率等；如果分析窄带信号，且有较强的干扰噪声，则应选用旁瓣幅度小的窗函数，如汉宁窗、三角窗等；对于随时间按指数衰减的函数，可采用指数窗来提高信噪比。通过选择不同的窗函数对它们的影响进行抑制，从而更好地降低设计要求，提高效率。

2 窗函数实现FIR数字滤波器的原理及设计

2.1 FIR数字滤波器的原理

数字滤波器的主要作用是通过改变原有的信号形式，估计信号的特征量，使得呈现信号中需要表达的最佳形式。FIR数字滤波器具有严格的线性相位，代表任意的幅度特性，单位抽样响应是有限长的，因而滤波器一定是稳定的，再用快速傅立叶变换(FFT)算法来实现过滤信号。其具体地原理是：寻求一系统函H(z)，使其频率响应H(ejω)逼近滤波器要求的理想频率响应Hd(ejω)，其对应的单位脉冲响应hd(n)。一个截止频率为ωc(rad/s)的理想数字低通滤波器，其传递函数的表达式是：

由上述公式可以得出，该滤波器具有无限性和因果性。为了得到有限长度的冲激响应函数，取样响应为h(n)，长度为N，其系数函数为H(z)：

同时也可以得到FIR数字滤波器输出y(n)的Z变换形式Y(z)与输入x(n)的Z变换形式之间的关系如下：

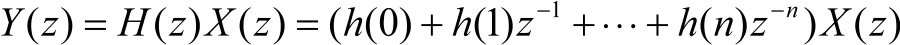
对上述表达式进行反Z变换可以得到：

【剧情回顾】《易筋经》是少林上乘内功秘笈，也是所有学武之人的向往。《天龙八部》中慕容复的侍女阿朱化装潜入少林寺中盗出此书，并为此身受重伤。后该书辗转被聚贤庄少庄主游坦之得到，不仅解了他身上的剧毒，还救了他一命。

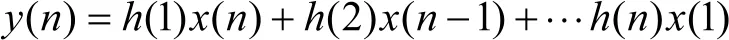
从上面的公式我们可以看出，在对滤波器实际设计时，整个过程的运算量很大，且在数字滤波器设计的过程中，还要根据设计要求，不断地调整滤波效果，以达到最优。在这种情况下，本文提出了利用仿真实验工具和窗函数综合进行设计，则可以快速有效地设计出FIR数字滤波器。

2.2 窗函数的应用

Hd(ejω)是矩形频率响应特性，故hd(n)一定是无限长序列，且是非因果的，而FIR滤波器的h(n)必然是有限长的，所以要用有限长的h(n)来逼近无限长的hd(n)，最有效方法是截断hd(n)或者说用一个有限长度的窗口函数序列ω(n)来截取hd(n)，即

利用窗函数设计FIR滤波器的具体步骤如下：

1）根据具体的性能要求通过对过渡带宽度Δω及阻带衰减AS，等参数的分析选择合适的窗函数，并估计滤波器的长度N。

假设存在一个低通滤波器，截止频率为ωc，满足线性要求。设低通特性的群延时为α，

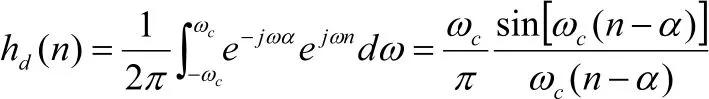
根据hd(n)是中心点在α的偶对称无限长非因果序列，矩形窗RN(n)在得到有限长的h(n)存在优势，即

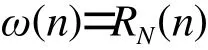
2）由给定的滤波器的幅频响应参数求出理想的单位脉冲响应和单位取样响应。但是按照线形相位滤波器的约束，h(n)必须是偶对称的，对称中心应为长度的一半(N-1)/2，因而必须α=(N-1)/2，所以有：

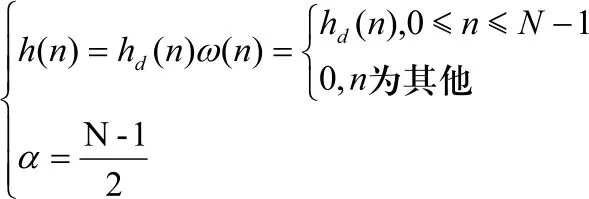
进一步得出：

3）验证技术指标是否满足要求。分析所设计的滤波器的幅频特性，按照复卷积公式，在时域是相乘、频域上是周期性卷积关系，即

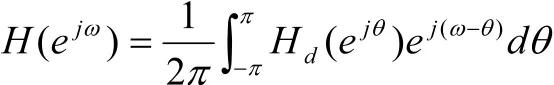
对矩形窗RN(n)，则有

WR(ejω)就是频域抽样内插函数，其幅度函数WR(ω)在ω=±2π/N之内为一个主瓣，两侧形成许多衰减振荡的旁瓣，如果将理想频率响应也写成

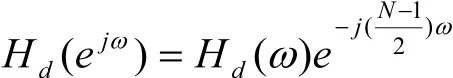
则其幅度函数为

从FIR滤波器的频率特性就能看出，加窗处理后提高了对频率的响应。窗函数的频率特性W (ejω)使得 H (ejω)在很大程度上逼近 Hd(ejω)。此时，h(n)=h(N-1-n)同时满足了线性相位的特征。

3 结束语

窗函数法的优点是简单，有闭合形式的公式可循，因而很实用。窗函数法是从时域出发，通过一定的窗函数截取有限长的单位脉冲响应来逼近理想单位脉冲响应；频率抽样法则是从频域出发对理想脉冲响应的逼近。所设计的数字滤波器和传统设计的滤波器比较,频率响应同理想频率响应之间的逼近误差最小,速度提高了很多,设计过程得到了很大的简化,方便了开发设计。

[1] 黄大卫. 数字滤波器[M]. 北京: 中国铁道出版社. 1991.

[2] 丁美玉, 高西全. 数字信号处理[M]. 西安: 西安电子科技大学出版社. 2001.

[3] 常迥. 数字信号处理[M]. 北京: 地质出版社, 1980.

[4] 楼顺天, 李博菡. 基于窗函数的系统分析与设计——信号处理[M]. 西安: 西安电子科技大学出版社. 2000.