宜春市烟草公司物流配送线路优化①

陈小丽， 曲 媛， 肖 鸿

(1．同济大学铁道与城市轨道交通研究院，上海201804;2．上海市城市建设设计研究总院，上海200125;3．北京交通大学交通运输学院，北京100044)

0 引言

配送是物流活动中直接与消费者相连的重要的环节，在物流的各项成本中，配送成本占了相当高的比例[1]．因此，配送线路是否合理直接影响着配送的速度、成本和效益等，如何科学合理地确定配送活动中的配送线路是一项非常重要的工作．

目前烟草行业的很多商业企业已经实行由物流中心直接配送到户的对接配送模式．本文针对宜春市烟草公司各分公司的需求情况、道路交通网、企业车辆及运行限制等因素进行了较充分的分析，利用节约里程算法对公司的配送区域和线路规划进行设计与优化．结果较为理想，可降低运输成本，提高效益．

1 节约算法

节约算法是用来解决运输车辆数目不确定的VRP问题，它是迄今为止用来解决VRP模型最常用的一种启发式算法．

节约算法主要步骤

基本条件:已知车辆的集合NT={1，2，…，m}，各车辆最大载重量为Wi，各配送节点组成的点集为NR={1，2，…，n}，各节点的需求量为Ri，各个节点之间的最短距离为cij．

(1)将车辆按照最大载重量从大到小依次排序，满足W1≥W2≥ … ≥Wi≥ … ≥Wn．

(2)计算所有的客户对(i，j)的节约里程的Δcij值，其中

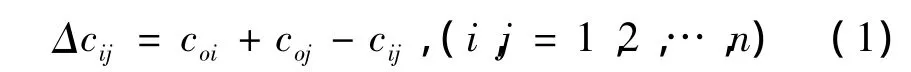
将其中大于0的Δcij从大到小依次排成队列．

(3)求可行解．确定各车辆的配送点集I1，I2，…，Im，令Ij={j}，(j=1，2，…，n)(先对各点进行单点配送)．

(4)合并配送路径．直到节约里程Δcij的队列空为止，重复下列步骤:按照节约里程Δcij队列从大到小的顺序，分析客户i和j之间合并的可能性(是否满足装载限制条件、不在同一路径内以及合并次数不超过2)，将i，j连接起来，即可令Ii'=Ii∪Ij;Ij=Ø．如果不是这样，则从节约里程队列中去除当前的节约里程，分析下一个客户对[2]．

2 VRP模型的建立

2．1 VRP 模型

多回路运输问题现实生活中十分普遍的一种调配问题．解决此类调配问题时，核心问题是如何对车辆进行调度．因此就出现了VRP模型，并成为解决这种运输问题的一个很成功的模型．

VRP模型问题描述为:确定一个配送中心，该中心有N辆车，对M个节点进行配送，每个节点的需求量是Ri(i=1，2，…，n)，每辆运输车辆的载重限制是D．设cij表示节点i到节点j的运输成本，如时间、路程和花费等．[3]配送中心编号为0，各配送节点标号为i(i=1，2，…，n)，定义变量如下:

建立此问题的数学模型:

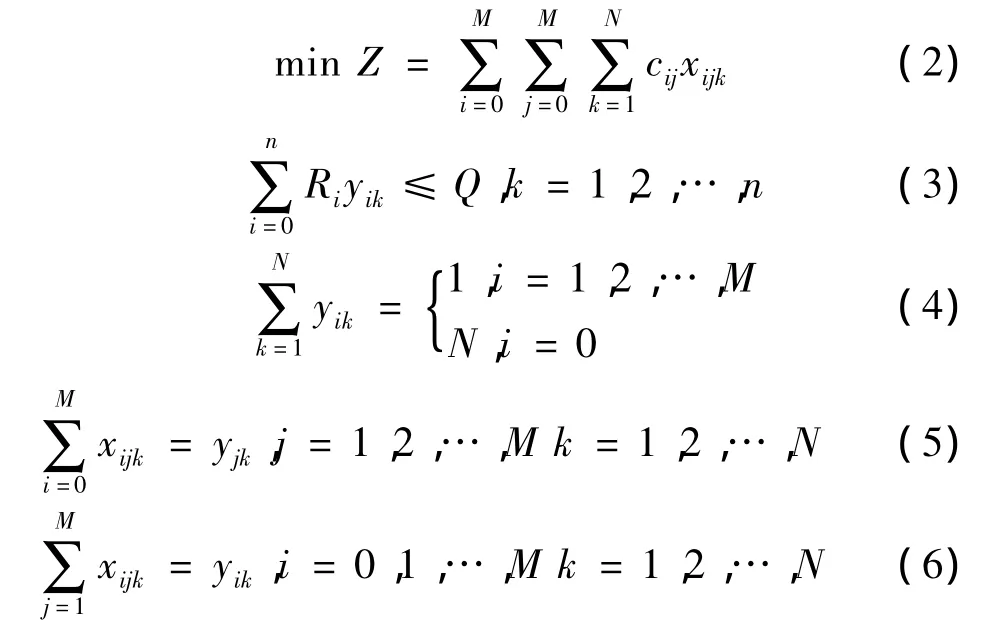
该模型中，式(3)为车辆的容量约束;式(4)保证了每个节点的运输任务仅由一辆车完成，而所有运输任务则由N辆车协同完成;式(5)和式(6)限制了到达和离开某一节点的车辆有且仅有一辆[3]．

图1 原有配送线路图

图2 节约算法求解线路结果

2．2 以宜春市烟草公司为例建模

2．2．1 宜春市烟草公司配送现状分析

宜春市烟草公司位于宜春市袁山大道，旗下设有十个分公司．该公司总部设有一个总配送中心，由该中心向旗下的十个分公司进行配送，再由十个分公司的配送中心将卷烟送往各地的零售商．由于需求量不断增大，现今该公司实行每日定点定量配送．需求量大的县市日需求量达到460多件，需求量小的县市则为60多件．公司现拥有5辆5t的货车，5 辆2．5t的货车，5t货车可装卷烟 330 件，2．5t货车可装卷烟150件，每件卷烟约15kg，所以当货车装满时仍然不会超重．

现在公司采用的是“点到点”的直接配送模式．其配送模式如图1所示．共需10辆货车，该模式的缺陷在于:首先，配送线路选择不够合理，没有得到优化，导致配送成本过大;其次，采用此种模式使得剩余货运量在进行直接配送时出现货车装不满，造成资源浪费，导致配送成本进一步加大，严重影响公司的效益．

2．2．2 模型的目标

确定所需要的车辆的总数n、车辆的类型以及它们的路线，并将这些车辆放在同一个回路中，同时包括回路内的路线安排和调度，使总费用最小．2．2．3 限制条件

(1)基于人性化的考虑，司机每天工作不超过6小时(配送车辆的车速一般控制在50km/h．)由于在本模型中考虑时间窗的限制会加大解题的难度，因此对配送时间的限制转换为在规定时间内对行驶里程的限制，即各车最大运输距离为500km．

(2)完成任务之后每辆车都要回到0处．

(3)不允许超过车辆的最大容量限制．由于用一辆5t货车的运量约为2．5t货车的2倍，并且在运输路径、物流成本方面也会有很大的节约，因此先选用5t的货车限制容量．5t货车最多装330件，2．5t货车最多装150件．

3 运用节约算法对宜春市烟草公司物流配送线路进行优化

已知市烟草公司为0点，分别向10个分公司配送卷烟，其拥有5辆5t的货车和5辆2．5t的货车，5t货车最大载重量为330件，2．5t货车最大载重量为150件，设各点间的距离为C，C={cij|i，j=1，…，10}，节约距离为 Δcij．每辆车的载重量为ri，各点需求量为Ri(i=1，…，10)，每辆车的行驶里程为Li(i=1，…，10)，且Li≤500km，袁州区为0 点，客户点1，2，…，10，现有的配送量如表1．

车辆调度采用以下方案:按需求量的多少选配车辆．如，袁州区分公司的需求量为372件，可先采用1辆5t货车进行一次直接配送，剩余42件使用节约算法的原理进行配送，其他各县市的货运量均按该方法进行整理，整理后如表2所示．

3．1 运用节约算法优化配送线路

在表2中，采用节约算法对有剩余货运量的10个县市进行配送线路优化．

3．1．1 确定各配送点间的最短距离

因为cij=cji，各分公司间最短距离如表3所示．

表1 现有配送任务表

表2 整理后的配送任务表

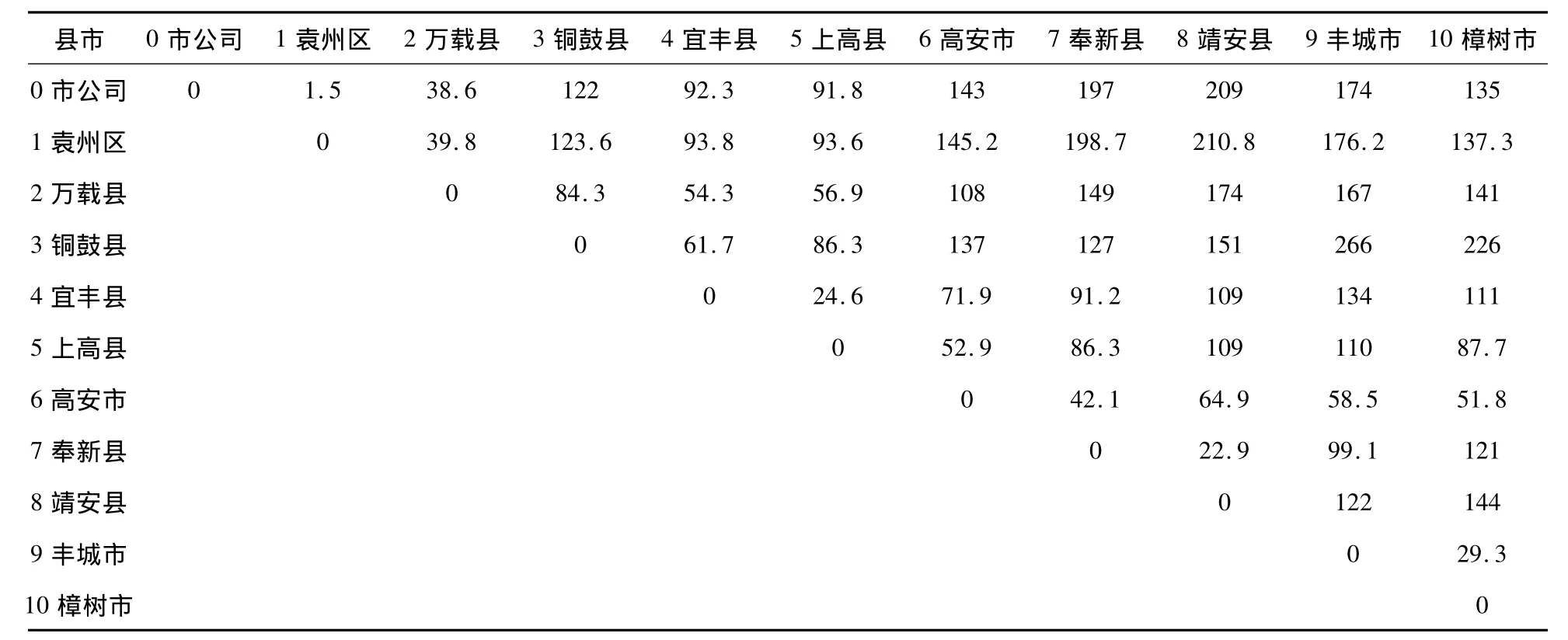
表3 各分公司间最短距离表(单位:km)

表4 节约里程顺序表 (单位:km)

3．1．2 求节约里程

根据最短距离表，计算出用户间的节约里程，并由大到小排列，编制节约里程Δcij顺序表，如表4所示．

3．1．3 求初始解

令Ii={i}(i=1，…，10)，最短路径Li=2c0i(i=1，…，10)，且Li≤500km，载重量ri=Ri，且Ri≤330件，对10个客户点进行标记B1=B2=…=B10=0，且Bi≤2．

3．1．4 优化结果

按节约里程从大到小合并路径得到的优化结果如表5所示，优化线路结果如图2所示．

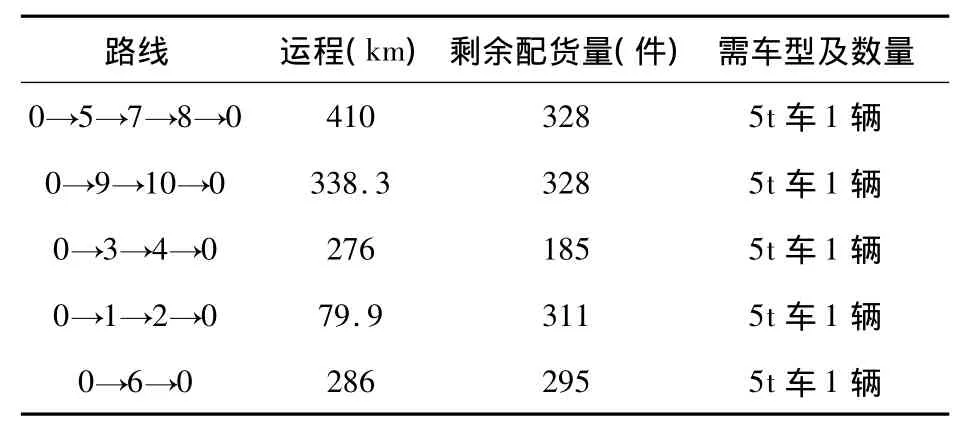
表5 节约算法优化结果

总运输里程为所有路径之和，求得为1390．2km，共需5t车4辆．与优化前相比，节约了5辆2．5t的车，节约里程数为1018．2，使得公司的配送效率大大提高．

[1] 雷同飞，张宏．物流配送中的车辆路径优化问题[J]．商场现代化，2009(1):119 －120．

[2] 刘利军．张裕集团葡萄酒配送线路优化研究[J]．山东工商学院学报，2006(1):98．

[3] 蔡临宁．物流系统规划—建模实例分析[M]．北京:机械工业出版社，2003．