信息系统下的工程保障能力评估

肖 宇，卢厚清，黄清禄，赵铜星

( 解放军理工大学 工程兵工程学院，南京 210007)

未来战争将是信息化条件下的联合作战，交战双方多以高新侦察、探测技术锁定重要的军事和经济目标，并应用远程精确制导武器实施高强度的火力打击，使后方仓库、机场、港口码头等重要工程设施遭到严重破坏。如何在敌方精确打击下对我方的重要工程设施和武器装备进行保障，或者在其受到打击的情况下对其进行修复和防护，怎样对我方工程保障能力进行评估，这些问题都将是军队信息化建设的重点。

我军工程兵部队保障能力的评估开展得比较晚，工程保障能力评估系统较为复杂，指标构成的因素较多，指标体系难以确立。关于工程兵作战工程保障能力评估的研究，包括以内容进行理论性探讨的形式散见于学术文章之中，或对某一方面观点的分析优化的学术文章中，也有对传统的机械化工程保障能力展开的评估文章中。对工程保障能力评估的研究，其泛泛的理论探讨相对容易，而从指标入手、通过建立模型来分析研究的方法无疑要复杂和困难得多，而且目前在信息化不断充实军队的今天，对信息化条件下的工程保障能力评估，仍属于空白，机械化的工程保障中融入信息能使得工程保障能力更具信息时代的特点，因此需要建立适应信息化战争的评估指标体系，来对工程兵遂行作战任务的能力进行客观的评价，以为工程保障的信息化建设和保障能力的提高提供科学的依据。

1 区间直觉模糊集的基本概念

定义1［1-2］设X 是一个非空集合，则称

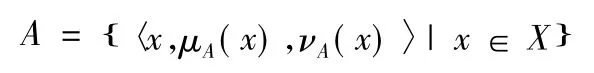
为直觉模糊集，其中μA( x) 和νA( x) 分别为X 中元素x 属于A 的隶属度和非隶属度，即

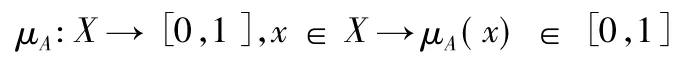
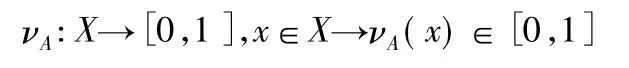
且满足条件

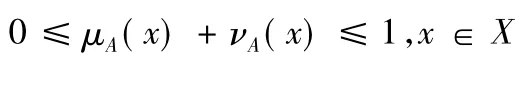
此外

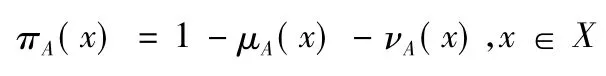
表示X 中元素x 属于A 的犹豫度或不确定度。

在直觉迷糊集的基础上，Atanassov 和Gargov 对其进行了推广，给出了区间直觉模糊集的概念。

定义2［3-4］设X 是一个非空集合，则称

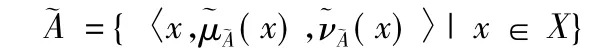
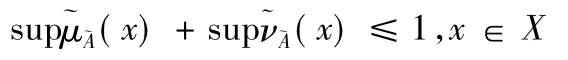
定义3［5］设为区间模糊直觉数，则

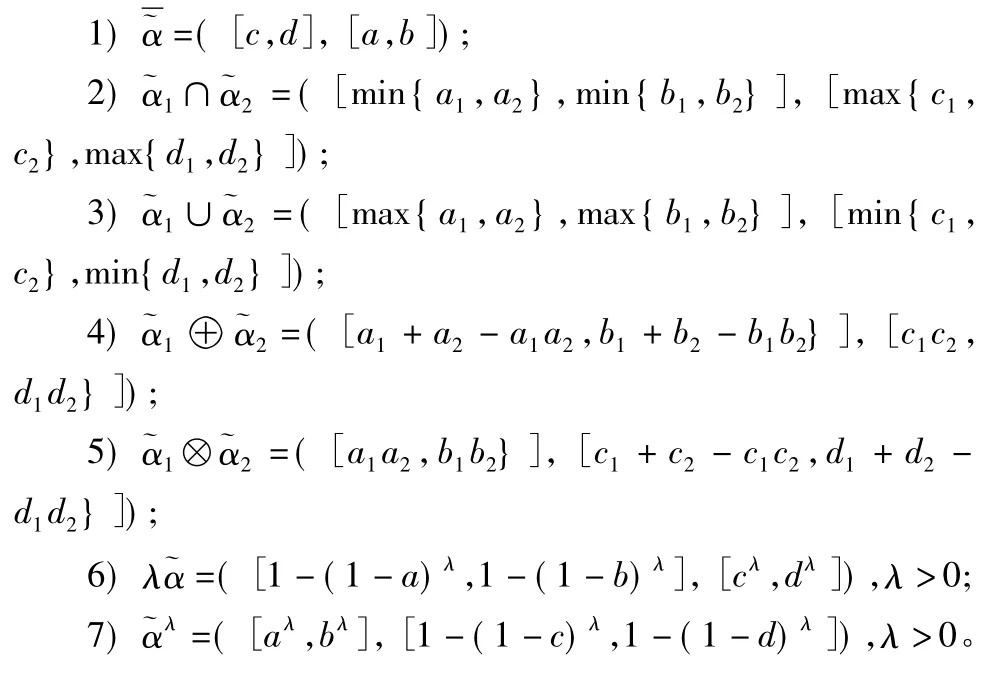
由上述有关区间直觉模糊数的运算法则运算结果仍为区间直觉模糊数。

定义4［7-8］设为一组区间直觉模糊数，且若

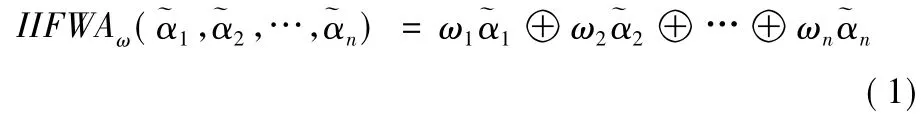
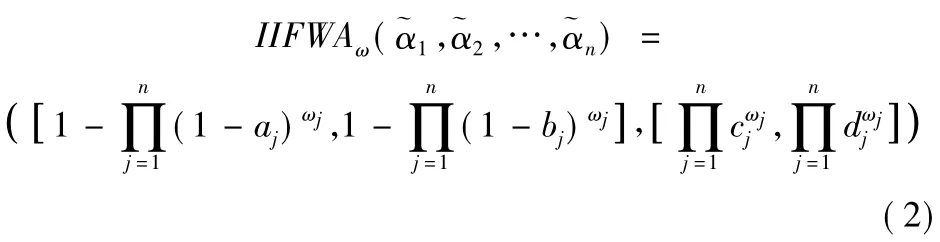
定义5［9］设为任意2 个区间直觉模糊数，则

2 属性权重已知条件下区间直觉模糊综合评价原理

在综合评价中［10］，用A={a1，a2，…，an}，表示影响评价目标的因素集，并且先对单一因素进行评判，对各因素赋予权重，进行二级评判;三级或更多级的综合评判依此类推。

区间直觉模糊综合评价过程分为以下几步。

1) 根据综合评价目标要求，确定综合评价的指标体系

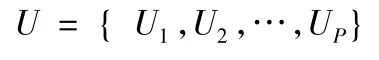
2) 按照每个指标的重要性来赋予与指标相对应的权重

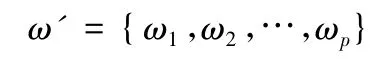
3) 根据评价对象的水平划分为若干评语等级( 状态)

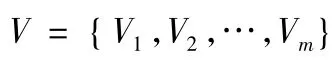
4) 建立区间直觉模糊关系矩阵R，~rij为区间直觉模糊数，表示被评价单位的第j 项指标在第i 评语等级的隶属度和非隶属度

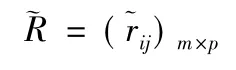
5) 计算区间直觉模糊合成值B

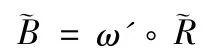
即

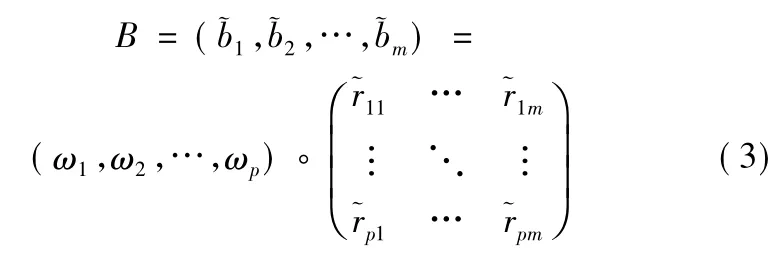
其中: ◦为区间直觉模糊集成算子。

若是单级评价，则按照区间直觉模糊数比较大小的方法，对~b1，~b2，…，~bm进行比较排序，确定其评价等级; 如果是多级评判，则还需要进行更深一层的评价。

6) 根据上述方法分别求出各因素的区间直觉模糊合成值( B1，B2，…，Bn) 。

7) 对因素集中各元素赋予相应的权重

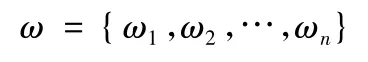
8) 根据各因素的权重ω，进行第二级综合评判

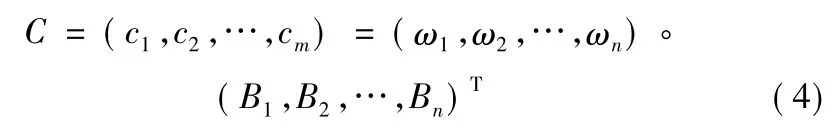
9) 比较c1，c2，…，cm的大小，若ci最大，则认为被评估对象最终评语等级为Vi。

3 属性权重信息不完全条件下区间直觉模糊综合评价原理

在多阶段多指标综合评价中，由于影响评价目标的因素很多，对单因素评价的指标体系也相对复杂，在评价过程中，指标体系中各指标的权重信息不完全给定，或者影响因素的权重具有不确定性。对于指标权重信息未给定或属性信息不完全的情况，需要根据可得到的信息，对权重进行计算确定，再按照权重信息已知的方法进行评估。

熵［11］本是热力学中的概念，后由Shannon 引入到通信系统中，熵反应了信源的平均不确定性大小，因此，评价指标属性上的模糊指标值可由相关专家给出模糊数，而各方案在某个属性的属性值变异程度越大，该属性的信息熵越小，该属性提供的信息量越大，即该属性在方案排序中所起的作用越大，从而该属性的权重也应该越大;反之，某个属性的属性值变异程度越小，该属性的信息熵越大，该属性提供的信息量越小，即该属性在方案排序中所起的作用越小，从而该属性的权重也应该越小。因此，根据信息熵所能反映的性质，对各评价指标赋予相应的权重。

基于上述分析，给出基于区间直觉模糊评价矩阵确定属性权重方法的具体步骤。

2) 计算规范化后各评语等级在各评价指标上的得分函数值，得到得分函数值矩阵并将其进行归一化处理，得为了避免得分函数小于0 的情况，这里取作为新的得分函数。所以有:

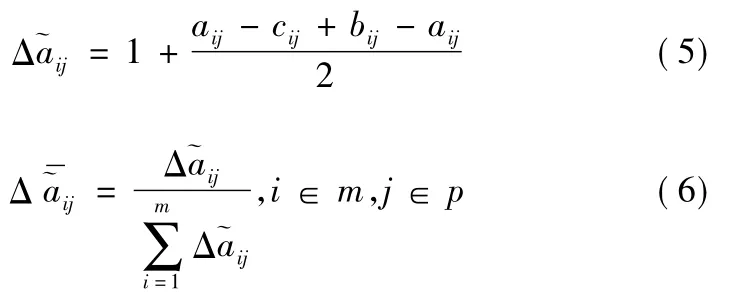
3) 计算各评价指标的Ui的输出平均信息量( 熵)

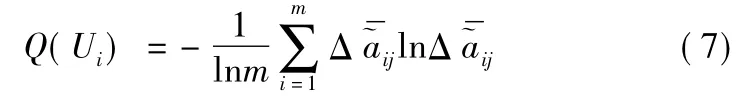
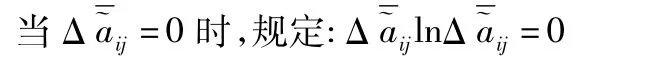
4) 求得评价指标体系的权重向量ω=( ω1，ω2，…，ωp)

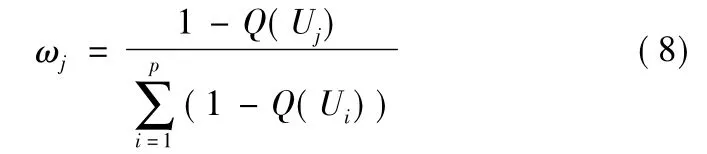
4 实例分析

现针对某单位工程保障能力进行评估，首先对其整个工程保障体系结构进行剖析，其指标体系有以下几个方面构成:1) 阵地工事系统抗打击能力;2) 阵地工事系统破坏后修复能力;3) 阵地工事不同程度损伤后保障能力; 4) 机动工程保障系统破坏后修复能力;5) 机动工程保障系统抗打击能力;6) 机动工程系统不同程度损伤后保障能力。经过调查统计，其各项指标的评价数据如表1 所示。

下面用本文所述方法，对该单位工程保障能力进行评估，其步骤如下。

步骤1 有上述信息，可知其评价指标体系由上述6 个指标组成，评语等级分别为: 优秀、良好、一般、合格和不合格。

步骤2 由于各指标的权重未知，需要求对应的权重向量。

1) 区间直觉模糊评价矩阵由表1 给出，因此本步骤省去。

2) 根据式(5) 计算各评语等级在各指标上的得分函数值，如表2 所示。

根据式(6) 对表2 各列进行归一化处理如表3。

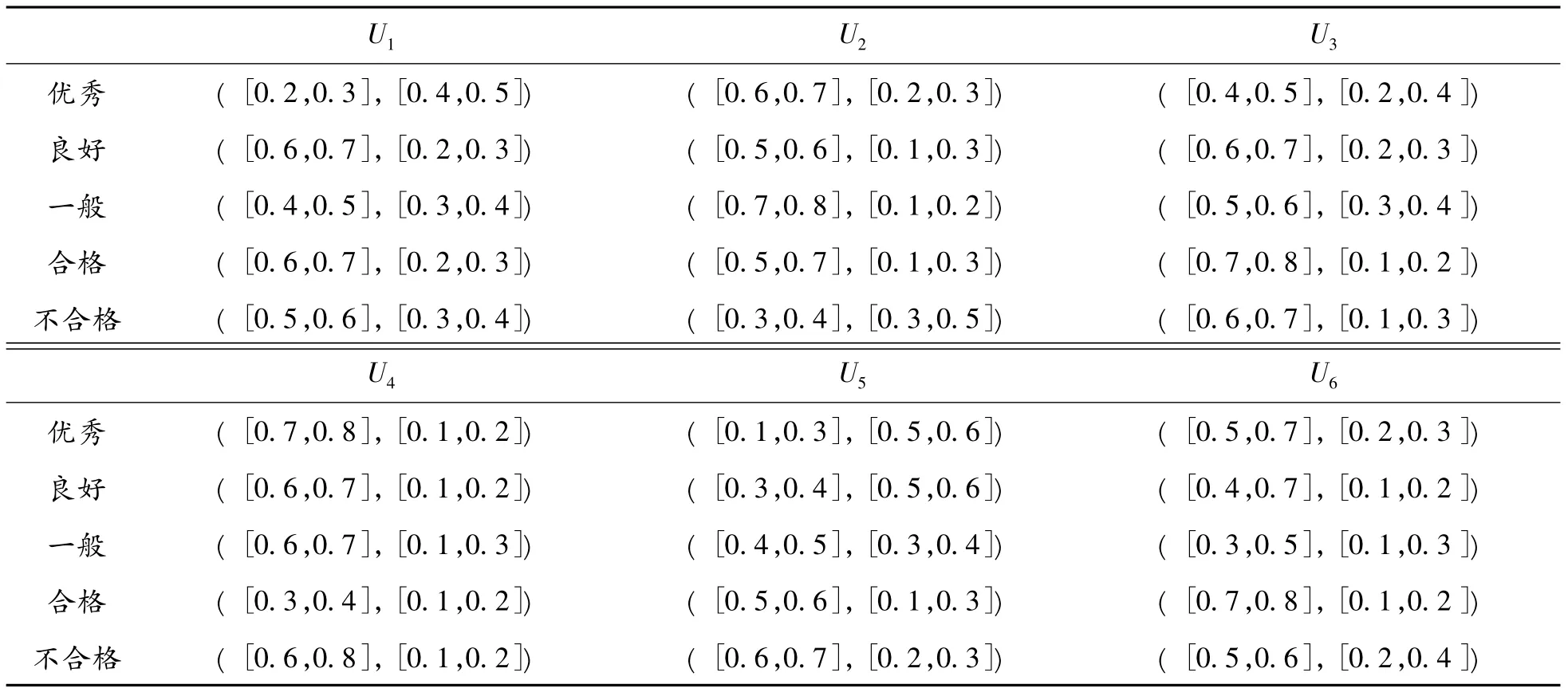
表1 评价矩阵

表2 指标得分函数值

表2 指标得分函数值

U1 U2 U3 U4 U5 U 6优秀 0.8 1.4 1.15 1.6 0.65 1.35良好 1.4 1.35 1.4 1.5 0.8 1.4一般 1.1 1.6 1.2 1.45 1.1 1.2合格 1.4 1.4 1.6 1.2 1.35 1.55不合格 1.2 0.95 1.45 1.5 1.4 1.25

表3 指标得分函数值归一化处理

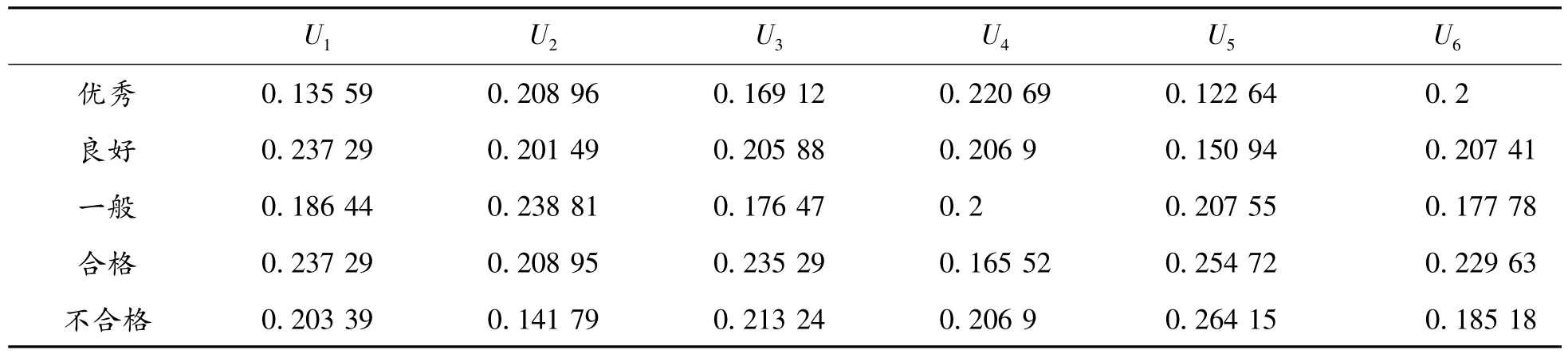
表3 指标得分函数值归一化处理

U1 U2 U3 U4 U5 U 6优秀 0.135 59 0.208 96 0.169 12 0.220 69 0.122 64 0.2良好 0.237 29 0.201 49 0.205 88 0.206 9 0.150 94 0.207 41一般 0.186 44 0.238 81 0.176 47 0.2 0.207 55 0.177 78合格 0.237 29 0.208 95 0.235 29 0.165 52 0.254 72 0.229 63不合格 0.203 39 0.141 79 0.213 24 0.206 9 0.264 15 0.185 18

3) 根据式(7) 计算各指标输出的信息熵:

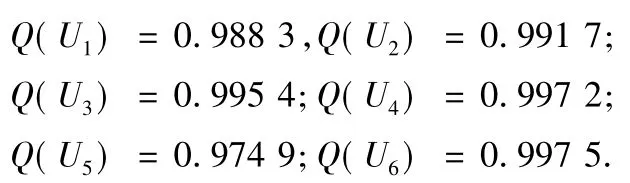
4) 根据式(8) 计算各项指标的权重，其结果为ω = (0.213 7，0.151 1，0.083 8，0.050 0，0.455 3，0.046 0)为便于计算，将权重向量简化为ω=(0.21，0.15，0.08，0.05，0.46，0.05) 。

步骤3 根据定义4 和式(3) ，求出各个评语等级的区间直觉模糊合成值

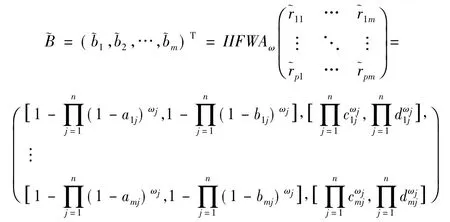
其计 算 结 果 为( ( ［0. 308，0. 458］，［0. 341，0. 461］) ，( ［0.454，0.569］，［0. 256，0. 396］) ，( ［0. 474，0. 580］，［0.228，0.350］) ，( ［0. 546，0. 664］，［0. 116，0. 279］) ，( ［0.542，0.648］，［0.211，0.342］) )T。

步骤4 根据定义5，将上述所求区间直觉模糊数大小进行比较。

分别求出的得分函数值S( ~bi) 为( - 0. 018，0. 186，0.238，0.408，0.319) ，其中i 依次为1，2，3，4，5，6。由比较结果可以确定，其评语等级为合格。

5 结束语

本文主要解决信息系统下的工程保障能力评估的问题。基于区间直觉模糊集的性质，将区间直觉迷糊数运用于综合评价之中，形成区间直觉模糊综合评价的方法。结合我军信息化建设的发展对工程保障能力的影响，从不同角度分析了工程保障系统的指标体系，对现今我军工程保障能力给予评估。

区间直觉模糊综合评价得出的评价结果更接近于真实值，能更精确地反映部队信息化建设的真实情况，对工程保障能力评估更准确。但当前我军信息化建设还不很完善，各因素的指标信息还需要进一步调查，特别是区间直觉模糊集对于数据调查的精确度要求更高，运用区间直觉模糊综合评价的方法对我军工程保障能力进行评估，需要进行进一步的数据收集，这也是下一步工作的重点。

［1］Atanassov K. Intuitionistic fuzzy sets［C］//Sgurev V. VII ITKR’s Session，Sofia，1983.

［2］Atanassov K. Intuitionistic fuzzy sets［J］. Fuzzy Sets and Systems，1986(20):87-96.

［3］A TANSSOV K.Intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1986，20(1):87-96.

［4］Atanassov K，Gargov G. Interval-valued intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1989(31):343-349.

［5］Chen S M，Tan J M.Handling multicriteria fuzzy decisionmaking problems based on vague set theory［J］.Fuzzy sets and systems，1994(67):163-172.

［6］Hong D H，Choi C H. Multicriteria fuzzy decision-making problems based on vague set theory［J］.Fuzzy sets and systems，2000(114):103-113.

［7］A TANSSOV K. New operations defined over intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1994，61(1):137-142.

［8］DE S K，BISWAS R，ROY A R.Some operations on intuitionstic fuzzy sets ［J］. Fuzzy Sets and Systems，2000(114):477-484.

［9］Xu Z S.Intuitionistic fuzzy aggregation operators［J］.IEEE Transactions on Fuzzy Systems，2007(15):1179-1187.

［10］苏为华.综合评价学［M］.北京:中国市场出版社，2005.

［11］孙秀德.军事后勤学［M］.北京:解放军出版社，1990.

［12］虞晓芳. 多指标综合评价方法综述［J］. 统计与决策，2004(11):119-121.

［13］冉东，柳少军. 基于复杂系统理论的指挥控制结构效能分析［J］.火力与指挥控制2010(12):45-49.