证据理论在热保护火工品高温安全性评估中的应用

王 飞，尹 霞，杜海深，徐 勇，梁 浩

（中国工程物理研究院总体工程研究所，四川 绵阳，621900）

异常高温火烧环境是一种典型异常环境，可以由多种异常事故引发。在异常火烧环境下，应避免火工品受热起爆导致的严重后果。为提高系统安全性，可采用钝感装药设计，以提高火工品的耐热温度及避免爆轰反应的发生。但在异常火烧环境下，环境温度会远高于装药的爆发点，此时，可以采用特殊的热保护火工品设计，控制、降低或隔离起爆器与传爆药、主装药之间的相互反应，最大程度降低战斗部主装药发生爆轰及爆炸反应的概率，提高产品安全性。

对于热保护火工品的安全性评估所需要的基础数据，可以直接通过火烧试验进行设计有效性的考核，但成本高昂且存在极大的不确定性。而目前基于证据理论的不确定性处理研究是一个广泛关注的课题，证据理论是Dempster首先提出后经Shafer系统化完善的，故又称Dempster-Shafer理论[1](简称D-S理论)。证据理论的研究重点在证据处理核概率推理，主要应用到决策判断领域及不确定性信息处理方面。在数据结构上，由于证据理论把点值函数形式推广到集合函数形式，其研究的基本对象是集合和区间数，因而证据理论在变大核处理不确定性上体现了很好的优势。证据的理解是宽泛的，证据不仅仅是通常意义下的实证据，如实验测量数据等，还包括人们的经验知识，包括人们对有关问题所做的观察和研究结果，也就是通常意义上讲的专家判断[2]，本文所采用的证据来源即为专家判断，对对象系统中的不确定性进行量化。

1 热保护火工品设计及安全性分析

1.1 热保护火工品设计

某自锻破片式爆炸序列设计如图1所示。图1中使用低熔点材料进行传爆药的装配连接，其熔点低于传爆药的爆发点。在异常高温环境下，低熔点材料将先发生熔化，导致传爆药及型罩脱落，避免由于传爆药受热起爆激活起爆序列，同时也形成了主装药空间的压力释放通道，最大程度地降低主装药发生爆轰及爆炸反应的可能性，实现预期的安全保护功能。

图1 热保护自锻破片式爆炸序列示意图Fig.1 Thermal protection of self forging fragment explosion sequence

1.2 异常火烧环节下产品的温升及失效模型

要进行系统安全性的量化评估，首先需要构建火工品装药环节及保护环节在异常高温环境下的温升模型。某次火烧试验中，火工品部位测得的温升曲线如图2所示。

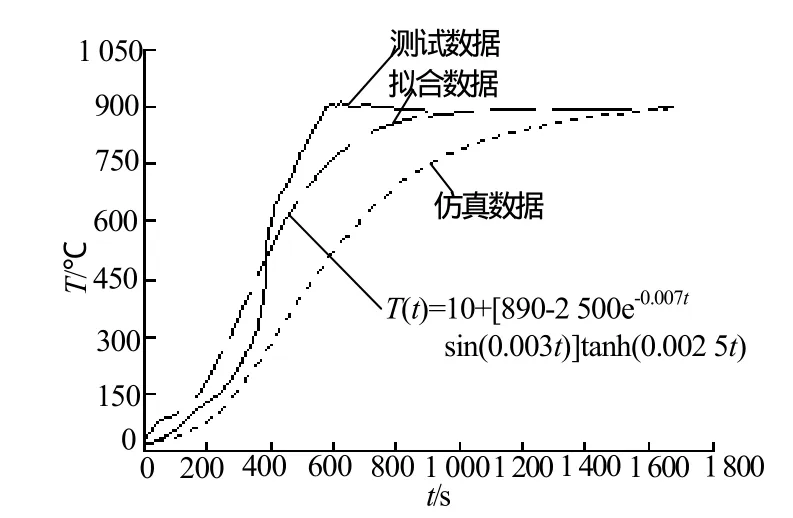
图2 火工品在高温异常火烧环境下的温升曲线Fig.2 Temperature curve of initiator in abnormal high temperature fire environment

系统整体有限元计算所得的温升曲线也见图2，从图2可以看出，实际的火烧温升曲线在温度上升过程中存在较大扰动，具有很强的不确定性，而有限元仿真过程获得的温升历程曲线较为平稳。

为了建立模型，更好地描述产品在火烧环境下的温升过程[3]，本文以双曲正切函数为主要形式，并包含衰减正弦扰动，构建温升过程，如式（1）所示，分别以Te（t）、Tp（t）表示装药及保护结构在t时刻的温度。从图2可以看出，使用该温升模型形式，较有限元分析更接近于试验温升历程。

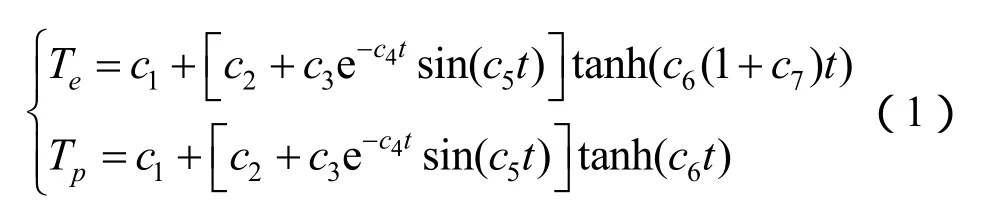
1.3 安全性分析模型

图3 热保护火工品安全性分析模型Fig.3 Safety analysis modle of heat-protected initiating explosive device

选定了拟合方程的参数，就可以确定结构的温升行为，从而对比分析产品的温升行为，判断装药与保护环节失效时间的先后顺序，以及火工品热保护的有效性，进而对系统安全性进行分析。热保护火工品的安全性分析模型见图3，图3中在时刻tF,p保护环节温度达到失效温度TF,p，此时，热保护结构失效；在时刻tF,e装药温度达到失效温度TF,e，此时装药爆炸失效。tF,p＜tF,e表明保护结构先于装药爆炸前失效，系统安全；反之，系统不安全。

进一步假设热保护火工品失效温度存在一定的概率分布，分别以fe(T)、fp(T)表示装药失效及保护结构失效的概率密度函数，假设其为正态分布形式，如式（2）所示：

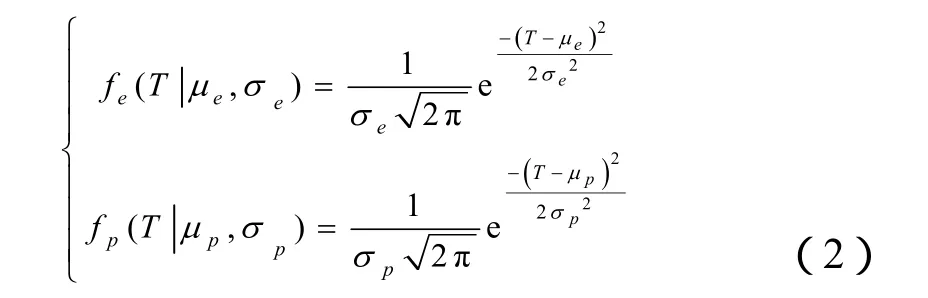
则对温度区间进行积分即可获得系统风险（不安全）概率的表达式：

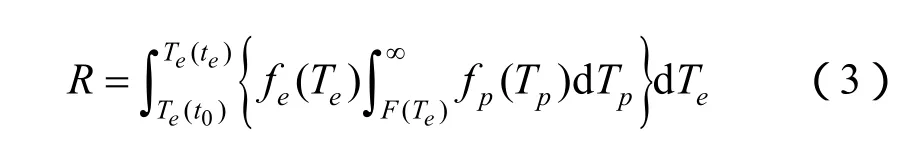
在安全性计算模型中，使用了c1～c7、μs、σs、μw、σw共11个特征参数，给定一组确定的参数，就可以根据式（3）得到了1个确定的风险概率的计算数值，各参数的物理含义及本文分析所假设的区间范围见表1。问题在于难以通过大量试验获得相关参数的统计范围及分布，在参数分布的确定过程中，存在认知不确定性问题。

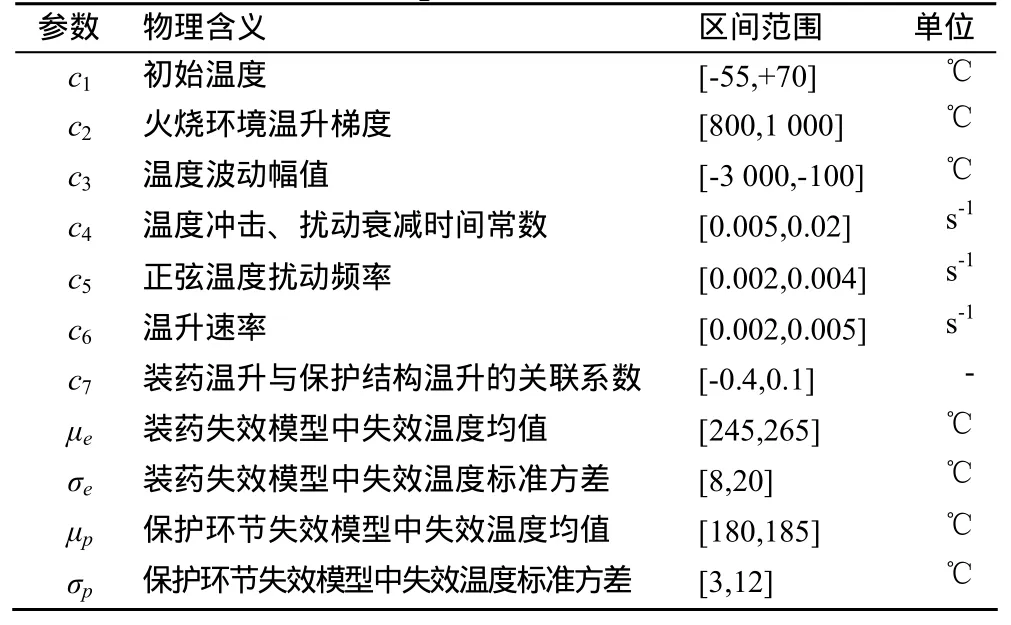
表1 分析模型涉及参数物理含义及分布区间Tab.1 Physical meaning and distribution for analysis model parameters

2 模型参数不确定性量化处理

2.1 证据理论基本数学原理

证据理论有多种解释和论述方法，其中应用最广的即基本概率分配(Basic Probability Assignment)函数，即mass函数[2]。设Θ为识别框架，基本信任分配函数m是一个从集合2Θ到[0,1]的映射，A表示识别框架Θ的任一子集，记作A⊆Θ，且满足：

式（4）中：m(A)称为事件A的基本信任分配函数，它表示证据对A的信任程度。

2.2 参数分布专家判断

假设有4位专家，对分析参数在给定区间上的分布做出了经验判断，如图4（a）所示。图4（a）中专家一认为参数在区间[a,b]内，但未给出子区间的分布；专家二将参数区间[a,b]等分为5个无交叉的等长子区间，每个区间分布相等；专家三将参数区间[a,b]分为5个无交叉的不等长子区间，且每个区间分布具有不同的分布密度；专家四将参数区间[a,b]分为有交叉的5个子区间，并假设在每个子区间上的分布密度为0.2。

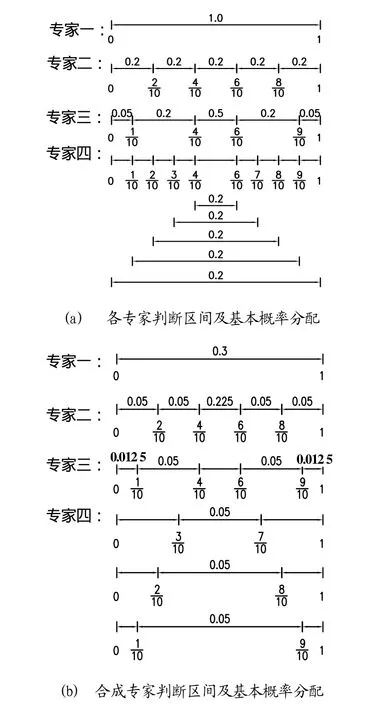
图4 专家对参数估计的经验判断Fig.4 Experts judgements of parameters estimation based on experience

根据各个专家给出的概率分布判断，就可以给出单个专家判断的各个区间子集的基本概率分配值，如式（5）所示[4]：

式（5）中：U为任意在区间[a,b]上的点的集合，Mi为单个专家所划分的区间范围。在假设每个专家的证据权重相同的情况下，就可以求得证据合成后的m值，即：

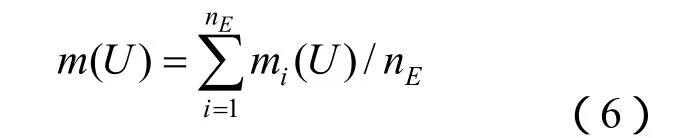
式（6）中nE=4，为专家数量，根据以上即可获得各个参数在区间上均一化处理后的基本概率分配值，如图4（b）所示，共13个区间子集。

3 安全性量化分析结果

按照图4（b）给出的各区间基本概率分配，进行模型参数的随机抽样，获得如图5所示的温升过程曲线。

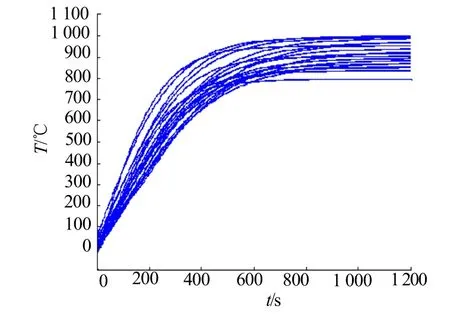
图5 随机参数抽样生成的温升曲线Fig.5 Temperature rise curve generated by random parameters sampling

对于每组参数，均可使用式（3）计算获得安全失效的风险概率。给出不同采样数N下风险概率的统计表达，如图6所示。

图6 热保护火工品安全性分析结果Fig.6 Safety analysis results of heat-protected initiating explosive device

图6中横坐标为在给定抽样参数的情况下，计算所得的风险概率R，纵坐标为计算所得风险概率＞R的抽样数占总抽样数的比值。从图6可以看出，抽样数N=200时，曲线有明显的波折，不平滑，在抽样数达到N=1 000时，曲线已经比较稳定和平滑，进一步增大抽样数，当N=10 000时，曲线走向及平滑趋势改善并不明显。表明在抽样数达到N=1 000时，计算结果已收敛，抽样数足以用于相关安全性的量化分析。

4 结论

在热保护火工品的异常火烧环境安全性分析中，假设了产品的温升模型，对于分析模型中涉及的不确定参数，采用证据理论中的专家判断方法，进行参数的不确定区间分布确定，成功用于处理热保护火工品安全性分析中的不确定性量化问题。基于此，完成了参数的随机抽样，并统计获得了系统的安全性定量分析结果。

[1]G.Shafer.A mathematics theory of evidence[M].Princeton:Princeton University Press,1976.

[2]段新生.证据理论与决策、人工智能[M].北京:中国人民大学出版社,1993.

[3]J.C.Helton，J.D.Johnson，W.L.Oberkampf.Probability of loss of assured safety in temperature dependent systems with multiple weak and strong links[J].Reliability Engineering and System Safety,2005,91(3):320-348.

[4]肖明珠.基于证据理论的不确定性处理研究及其在测试中的应用[D].成都:电子科技大学,2008.