基于二次变换的曲面投影图像校正技术研究
2012-07-06刘国华
刘国华
(黑龙江大学 机电工程学院,哈尔滨 150080)
0 引 言
许多虚拟现实应用系统中,为了增强虚拟环境的沉浸感,通常采用曲面显示屏,如圆柱形、球形屏等。计算机产生的图像都是针对平面显示,当投影到曲面上时,会产生几何失真。为使观察者能够看到正常图像,需对计算机产生的图像进行预变形处理,以抵消曲面显示屏造成的几何失真。目前主要是通过在图形工作站与投影设备间增加额外校正单元[1],或是专业投影设备本身内部集成校正单元[2],这些方法成本高,且灵活性较差。
曲面显示屏较常见的有球面、圆柱面等二次曲面形状,本文针对此种类型显示屏的投影显示,利用计算机视觉研究中的相关内容,推导了基于二次变换的图像校正关系式,研究了其求解过程,并通过实例对变换效果进行了验证。这种方法通过编程对投影图像预处理,不需增加额外设备,具有方便、灵活的特点。
1 计算机视觉与射影重建
1.1 相机模型
计算机视觉研究中通常利用相机模型来模拟人的视觉系统,并通过相机获取的物体的图像信息,计算对应三维物体的位置、形状等几何信息。线性相机模型是应用最为广泛的一种模型,表达了空间点与对应图像点之间的关系。
在投影系统中,投影仪将图像点投影在空间显示屏上,而该点在观察者观察系统所成的像即为观察图像点,因此可以通过显示屏曲面上的空间点求解投影仪图像与观察图像之间的关系。若将一相机置于观察者位置来代表观察者视点,且投影仪、相机均采用线性模型表示,则求解图像校正关系式就转化为求解显示屏曲面上的空间点在不同模型视图中的对应投影点之间的参数关系[3]。由于相机、投影仪模型都采用线性相机模型表示,因此在以下说明及推导过程中,不再从名称上区分二者,而以相机1、相机2进行描述。
在计算机视觉研究中,三维重建主要研究在欧氏几何意义下的重建,使用直角坐标系,坐标系之间变换为平移或正交变换。近年来研究表明,欧氏几何意义下的重建要求条件过多。从上世纪80年代开始,许多学者开展了射影几何意义下的三维重建研究,简称射影重建。相对于欧氏变换,采用射影变换有很多好处,通常不需求出投影矩阵,而仅通过不同视图间的图像点得到识别物体的射影变换不变量,从而实现更一般意义的三维重建[4]。
1.2 对极几何与基本矩阵
在射影重建过程中,一定意义下的相机间的相对位置关系通过对极几何关系和基本矩阵描述[5]。
由计算机视觉相关原理可知,从两个不同视点获得的同一场景两幅图像间存在着对极几何关系。如图1所示,空间点M在两个投影图像I1、I2的投影分别为m、m′;两个相机光心分别为O、O′,连接光心O、O′的直线为基线,基线与左右图像的交点e、e′为极点。根据成像几何关系可知,m、m′、O、O′、M 在同一平面π上,并且m、m′分别位于π与两个图像I1、I2的交线l、l′上,则直线l=<e,m>为m′在I1图像上的对应极线,直线l′=<e′,m′>为m在I2图像上的对应极线,并且每幅图像上的极线都交于该图像上的极点。
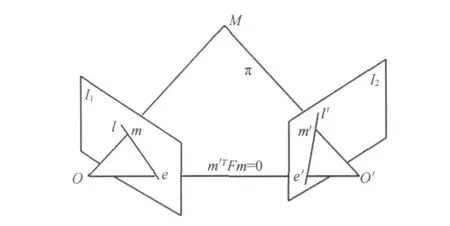
图1 对极几何关系Fig.1 Epipolar geometry of two projections
对极几何关系提供了极线约束条件,即:一幅图像上的点在另一幅图像上的匹配点位于该点在另一幅图像的对应极线上。对极几何的约束关系在代数上可以通过一个3×3的基本矩阵F表示,基本矩阵F将一幅图像上的点m映射到该点在另一幅图像的极线l′上,即有以下关系:

式中m、m′为空间点在不同投影视图上的对应点。
基本矩阵F可以通过两幅图像中的一组匹配点,由式(1)建立线性方程组求解获得。基本矩阵具有下述基本性质:
1)极点e满足Fe=0,极点e′满足FTe′=0;
2)F在相差一个非零常数因子下是唯一的;
3)若M1与M2分别为两个相机的投影矩阵,F为其基本矩阵,则基本矩阵为F的相机的投影矩阵均可表达为M1H与M2H,其中H为任意满秩4×4矩阵。这表明给定相机的基本矩阵后,投影矩阵并不唯一。
由以上内容,可得射影重建的一个重要方法:即在射影重建中,首先通过不同图像间的匹配点计算基本矩阵F;然后,对于两幅图像分解出两个形式相对简单的投影矩阵M1、M2,进而实现射影几何意义下物体的三维重建[6]。
2 二次变换参数关系式
二次变换关系式表达了二次曲面投影图像校正中的投影仪图像与正常图像之间的参数关系,其推导过程实质,即求解二次曲面上空间点在不同投影视图上的投影点之间的参数关系式。
2.1 二次曲面
日常生活中常见的球面、圆柱面等,都可以采用三元二次代数方程表示,通常称作空间二次曲面,可以表示为:

式中Q为二次曲面方程的系数矩阵,为4×4对称矩阵;X为二次曲面上点的齐次坐标,X=(x,y,z,1)T。
当二次曲面不过原点时,有Q(4,4)≠0,即常数项不为0,此时可令Q(4,4)=1,Q写成如下形式:
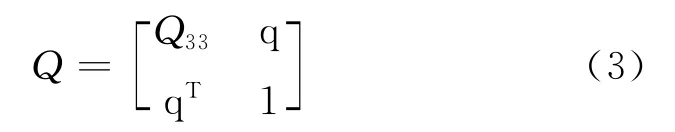
式中Q33为3×3对称矩阵;q为3×1向量。
二次方程系数矩阵未知量为9个,对应空间二次曲面的自由度为9,研究证明二次曲面可以由它在两幅投影视图上的9对匹配点实现三维重建[7-8]。
2.2 二次变换关系式的推导
对于已知基本矩阵F,对应相机投影矩阵并不唯一,在射影重建研究中,通常取两个较简单矩阵作为相机投影矩阵[9]:

式中M1、M2为相机投影矩阵;I为3×3单位矩阵;A为3×3矩阵,且A=e′×F;e′为极点。
如图2所示,对于空间二次曲面Q上一点P,令其空间坐标为XP;P点在两个投影视图ψ、ψ′上的投影点分别为p和p′,令其坐标分别为(x,y,1)、(x′,y′,1),两个视图的投影矩阵 M1、M2分别由式(4)、式(5)给出。
根据线性相机模型关系式,则有:

其中≅表示在相差一个非零常数因子意义下的相等。
由投影矩阵式(4)、相机模型式(6)可知,视图ψ上的图像点p对应的空间点P可以表示为(x,y,1,k),记为(p,k),其中k为与空间位置相关的量。则P点在视图ψ′上投影p′的坐标:
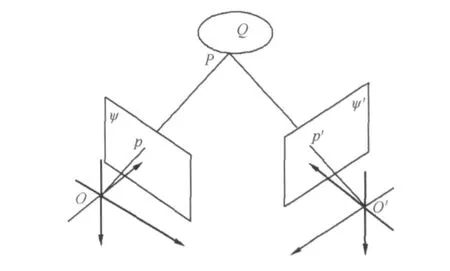
图2 空间二次曲面成像几何关系Fig.2 Projection of a point on quadric surface
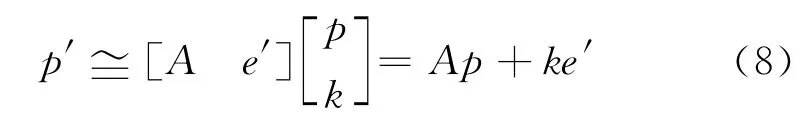
式(8)即为二次曲面上的一点P在不同投影视图上的投影点p和p′之间的参数关系式,式中的A、e′可以在求出基本矩阵以后得到,其求解关键在于求出k值,而k与二次曲面上的点位置相关。
由于P为空间二次曲面上一点,将P点坐标(p,k)代入二次曲面式(2)得:

式(12)即为二次曲面上一点在不同投影视图的投影点之间的参数关系式,即所求的图像校正二次变换关系式。由式(12)可见,二次变换关系式与投影视图参数A、e′以及二次曲面Q相关。由于直线与二次曲面通常会有两个交点,所以出现±号,可以通过一对匹配图像点坐标确定。
2.3 二次变换关系式的求解
二次曲面的三维重建研究表明,空间二次曲面可以通过两个投影视图中的9对匹配点实现重建,而射影重建中的基本矩阵可以通过8对匹配点求出。因此,二次变换关系式可以通过两个视图中的9对匹配点进行求解。
2.3.1 二次变换关系式求解算法
二次变换关系式的求解主要包括两部分内容:①求解基本矩阵F以获取式中的A、e′;②求解二次曲面的方程Q。根据空间二次曲面三维重建的相关内容,以上参数可以通过两幅图像中的9对匹配点求出,具体求解过程如下:
1)求解基本矩阵F和极点e、e′。这3个参数可以通过基本矩阵关系式(13)、极点方程式(14)和式(15),建立线性方程组进行求解。首先,利用8对图像匹配点通过式(13)建立线性方程组求解基本矩阵F;然后,将F 代入式(14)、式(15)建立线性方程组求解e、e′。
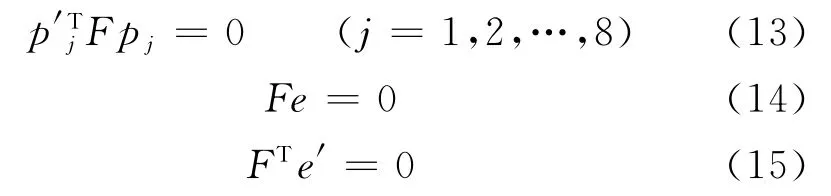
2)求解矩阵A。3×3矩阵A可以通过4对匹配图像点求出,通常取上一步求出的一对极点e、e′和另外3对匹配点,通过式(16)建立线性方程组进行求解,即可得出矩阵A[10]:

3)求解其余匹配点对应的kj(j=4,5,…,8)值。根据匹配点的坐标,利用上述所求得的A、e′,并通过式p′j≅Apj+kje′即可以求解kj。通常采用最小二乘法,由式(17)求解kj值:

4)求解二次曲面方程Q。将9对匹配图像点和对应的kj值代入式(18),建立线性方程组,即可得到二次曲面方程Q的各项系数:

通过以上步骤可以得出二次变换关系式(12)中所需的全部参数A、e′和Q,二次变换参数关系式即确定。
2.3.2 利用OpenCV求解二次变换关系式
为了求取二次变换关系式,需要对投影仪、相机图像进行处理(主要是特征点检测),并通过匹配点计算基本矩阵F,这主要借助OpenCV完成。
OpenCV是由Intel公司推出的一套可免费获得的由C函数和C++类所组成的库,主要用于实现一些常用的图像处理及计算机视觉算法,如特征检测与跟踪、运动分析、目标分割与识别以及三维重建等。OpenCV的源代码完全开放,源代码的编写简洁、高效,并且大部分函数都已经过汇编最优化,因此代码执行效率较高,近年来在国内外的图像处理及相关领域得到广泛应用。基本矩阵F在计算机视觉研究中占有重要地位,因此学者们也提出了多种求解算法。对于已知8对或以上匹配点的情况,经常采用8点算法和改进8点算法,它们都是易于实现的线性算法;另外还可以采用鲁棒算法,如RANSAC法。OpenCV中提供了专门的函数cvFindFundamentalMat()求解基本矩阵。对于二次变换关系式求解过程中的其它数学运算过程,主要借助Matlab所提供的函数库实现。
3 二次变换图像校正的实现及验证
二次变换图像校正的实现主要包括二次变换预处理和实时校正两个阶段。
在预处理阶段,首先通过投影仪投影特征图片到显示屏,并在观察者所处位置利用相机拍摄投影图片;利用OpenCV获取两幅图片中对应的特征图像点坐标,并根据前述算法求解二次变换关系式的各项参数。在实时处理过程阶段,计算机首先将图像存储到纹理缓存,然后利用二次变换关系式对纹理图片进行变换处理。在纹理缓存中的二次变换采用OpenGL编程实现,首先将理想图像作为纹理贴在由四边形或三角形组成的网格上;然后利用求出的二次变换关系式,对贴图网格的顶点进行位置变换,从而实现对理想图像的变形处理。
为了对二次变换图像校正法进行验证,采用圆柱面投影实验。特征点变换图片见图3,通过两幅图片中的对应特征点,即可求出二次变换关系式。根据获得的二次变换关系式,图4、图5分别为校正前、后的结果,可以看出,经过二次变换校正后的投影图像可以获得较好的显示效果。



4 结 论
本文主要研究了曲面投影图像的校正技术,利用计算机视觉研究中射影重建的相关内容,推导了用于二次曲面投影图像校正的参数关系式——二次变换关系式,阐述了二次变换参数关系式的求解方法和过程。通过编程,探讨了二次变换参数关系式用于二次曲面投影图像校正的实现过程,并通过实际投影对校正效果进行了验证。
[1]华利创通公司.华力公司推出全新SuperSonic视景仿真投 影 系 统 [EB/OL].http://www.hwacreate.com. cn/chinese/product/jjfan/SuperSonic. html,2004-03-15/2006-08-12.
[2]巴克公司.巴可公司协助SIGGRAPH 3D协同可视化应用大放异彩 [EB/OL].http://www.projectorwindow. com/projector/barco/barco-060809. htm,2006-08-09/2006-08-12.
[3]Rajeev J.Surati.Scalable self-calibrating technology for seamless large-scale displays [D].Ph.D.Thesis,Massachusetts Institute of Technology,1999:15-20.
[4]梅向明.高等几何 [M].北京:高等教育出版社,1983:88-90.
[5]龙熙华,梁 栋,李占利.基于L-M算法的射影重建技术研究 [J].西安科技大学学报,2005,25(1):81-84.
[6]马颂德,张正友.计算机视觉——计算理论与算法基础[M].北京:科学出版社,2003:90-92.
[7]汪令江.二次曲面的三维重建和轮廓线投影 [J].工程图学学报,1989,(11):38-52.
[8]A.Shashua,S.Toelg.The quadric reference surface:Applications in registering views of complex 3Dobjects[A].In Proc.European Conf.On Computer Vision[C].Stockholm.1994:569-581.
[9]R.Hartley.Projective reconstruction and invariants from multiple images[J].IEEE Trans.PAMI,1994,16(10):1036-1040.
[10]Amnmon Shashua.The quadric reference surface:Theory and applications [J].International Journal of Computer Vision,1997,23(2):185-198.
