基于二维EMD改进方法的图像边缘检测

赵 晨，周振国，崔 颖

（哈尔滨工程大学a.水声工程学院；b.信息与通信工程学院，哈尔滨 150001）

0 引 言

图像边缘检测是图像分析中的一个基本问题，好的边缘检测结果将会极大地改善后续的图像识别和理解系统的性能。常见的边缘类型有阶梯型边缘、屋顶型边缘和斜面边缘。传统的边缘检测方法主要有3类[1]：①微分算子法，如Robert算子、Sobel算子、Laplace算子等，这类方法实现简单，提取图像边缘速度快，但容易受到噪声的影响；②最优算子法，如LOG算子和Canny边缘检测法，但是LOG算子不能在检测性能和抑制噪声之间取得较好的平衡；③多尺度方法，这类方法是伴随着图像的多分辨率多尺度分析技术发展起来的，主要包括小波分析和经验模式分解（Empirical Mode Decomposition，EMD）技术等。

EMD是N.E Huang等人于1998年提出的一种全新的信号时频分析方法[2]；2003年J.C Nunes将一维EMD方法推广到二维领域，提出了真正意义上的二维经验模式分解方法[3－4]；2005年，刘忠轩提出了方向EMD[5]，并应用于图像分割；2010年梁灵飞提出了窗口EMD[6]，并将其用于医学图像增强等方面。

本文对传统的二维EMD方法进行了改进，采用该改进方法将原始图像分解为若干个不同尺度的IMF分量及一个余量之和，充分利用IMF1和IMF2分量的小尺度优势，结合灰度图像二值化、形态学细化提取图像的边缘[7－9]，仿真实验结果验证了该方法的有效性。

1 二维EMD改进方法

在将一维EMD方法推广至二维EMD的过程中，需要解决如下几个关键问题[10]，主要包括：①局部极值点（极大值点和极小值点）的选取方法；②二维曲面插值方法的选取；③边界效应的处理；④SD停止准则；⑤二维EMD分解停止准则。

1.1 传统二维EMD方法

传统二维EMD方法的基本流程：

1）对原始图像提取极大值和极小值点集；

2）对极大值点集和极小值点集分别进行曲面拟合，经插值获得极大、极小值点曲面包络，求其平均得到均值曲面包络；

3）计算原始曲面与均值曲面包络的差值；

4）计算SD终止条件。

不断重复步骤1）～3），直到满足二维EMD分解停止条件得到第一个固有模态函数（Intrinsic Mode Function，IMF）IMF1，用原始图像减去第一个固有模态函数得到第一余量，对余量重复步骤1）～4），就可以依次得到图像的若干个固有模态函数和最终的一个余量。

1.2 改进的二维EMD方法

传统二维EMD方法的详细实现过程比较复杂，也没有抑制边界效应，其分解性能有待进一步提高。本文从实用的角度出发，给出了一种易于实现的二维EMD改进方法。设原始二维图像f（x，y）是一幅m×n像素大小的灰度图像，则该改进的二维EMD算法的具体实现分为如下3个步骤：

步骤1：输入图像预处理。为了减弱边界效应的影响，将原始灰度图像f（x，y）上下左右做镜像延拓，得到延拓后的M×N预分解图像F（x，y），其中M＞m，N＞n。

步骤2：图像F（x，y）的二维EMD分解。分4小步实现：

1）外部初始化，先令待处理的图像为：

r0（x，y），r0（x，y）＝F（x，y），j＝1。2）筛分获得第j个IMF分量：

a.内部初始化：令k＝1，hk－1（x，y）＝rj－1（x，y），即h0（x，y）＝rj－1（x，y）；

b.采用8邻域点与中心像素点灰度值比较的方法，找出hk－1（x，y）中的所有极大值点和极小值点；

c.分别对极大值点集和极小值点集采用Delaunay三角剖分和三次多项式（cubic）插值相结合的方法进行曲面拟合，形成二维图像上下包络umax（x，y），umin（x，y）；

d.计算均值包络：

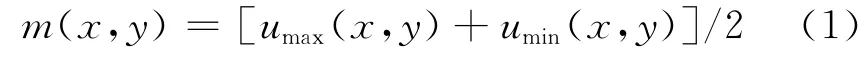
e.从图像中减掉均值包络得到：

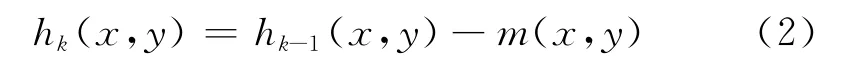
f.计算终止条件SD，若标准偏差SD小于给定的门限值λ，则有cj（x，y）＝hk（x，y）；否则令k＝k＋1，转到b步。

3）求余量：rj（x，y）＝rj－1（x，y）－cj（x，y），若rj（x，y）中仍有≥2个极值点或者分解所得到的IMF数目未达到要求，将rj（x，y）看作新的数据转到2），令j＝j＋1。

4）得到预分解图像F（x，y）的BEMD分解表达式：

其中，SD的计算式如式（4）所示，阈值λ根据经验可取为0.1～0.3：

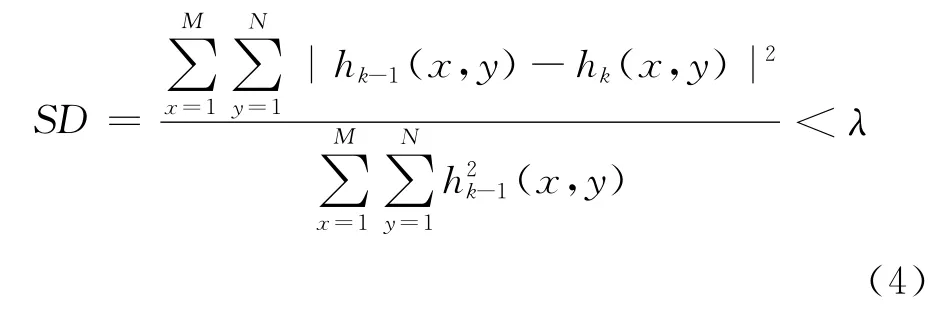
步骤3：提取原始图像f（x，y）的分解结果。根据步骤1和式（3）即可提取出原始图像f（x，y）的二维EMD分解结果表达式为：

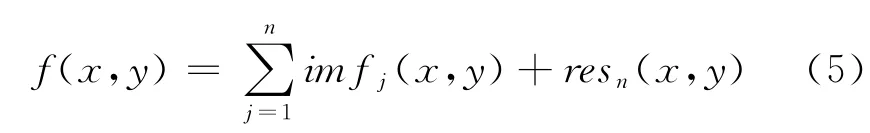
其中f（x，y），imfj（x，y），resn（x，y）依次取F（x，y），ci（x，y），rn（x，y）中心对应的m×n区域部分。

这样就将一幅灰度图像按照尺度由小到大分解为若干个二维固有模态函数分量和一个大尺度余量之和的形式。需要说明的是，对于步骤2中的第3）步，可以采用固定IMF个数的方法，例如仅仅分解前3个或4个二维固有模态函数和一个余量图像。因为图像分解停止条件太严格的话，分解会得到过多的IMF分量，导致最后几个IMF分量的意义不大。

采用此二维EMD改进方法分解一幅512×512像素大小的Lena图像，阈值取λ＝0.1，分解得到3个IMF和一个余量图像，实验结果见图1。各IMF反应了原始图像不同尺度的细节信息，余量反映了趋势信息。

图1 Lena图像的二维EMD分解结果Fig.1 EMD decomposition results of Lena image in 2D

2 基于二维EMD的图像边缘检测

由图1可见，Lena图像分解结果中的IMF1和IMF2图像中包含有较多的细节信息和边缘特性，而IMF3图像轮廓比较模糊，不利于提取边缘，因此本文中充分利用IMF1和IMF2的边缘细节特性来提取Lena图像的边缘。

基于二维EMD改进方法的图像边缘检测的具体实现方法的流程见图2。先将原始图像进行二维EMD分解获得IMF分量和余量图像，提取出IMF1和IMF2进行灰度二值化处理，再将该二值化图像在形态学领域作细化处理若干次[11]，提取最终的结果即为原图像的边缘，其中细化次数的设定取决于边缘图像的视觉质量。

在图2中的二值化时，可以采用反复试验的方法来设定合适的阈值，一般来讲，阈值增大，边缘线将会变得模糊不清或者消失；相反地，阈值减小，点状噪声就会增多。除此之外也可以尝试直方图的方法来进行灰度图像二值化。文中采用人为设定阈值的方法进行二值化。

图2 边缘检测流程图Fig.2 Flow chart of edge detection

图2中的形态学细化是在阈值处理后的二值图像上进行的，通过去除像素点使目标孔洞变为最小细环线，是把线宽不均匀的边缘线整理成同一线宽（一般为1个像素宽度）的处理。在Matlab 7.1编程环境中使用数学形态学中的bwmorph函数，函数参数为thin[11]，也可以指定细化的次数，将图像细化，并保持连通性。

3 实验结果与分析

基于以上内容，文中做以下两个实验，具体如下：

实验1：仅利用图1中的IMF1图像，先对其选取合适的阈值作二值化处理（实验中阈值为0.57），然后对此二值化图像采用数学形态学中的“细化”操作，实验结果作为原图像的边缘。

实验2：仅利用图1中的IMF1和IMF2图像，实现原图像的边缘细节重构，对重构图像选取合适的阈值作二值化处理（实验中阈值为0.51），然后对此二值化图像采用数学形态学中的 “细化”操作，实验结果作为原图像的边缘。

实验1和实验2的实验结果见图3，比较图3（c）和图3（f）发现，图3（f）的边缘更加清晰，甚至Lena所戴的帽子的褶皱都清晰可见。由实验结果图像可见，采用基于二维EMD改进方法的图像边缘检测具有实际可操作性。

另外，图4中的实验图像为512×512像素大小的Lena图像，采用不同算法的边缘提取结果的比较。比较发现，本文采用的两种方法所提取的的边缘细节特征更加细腻，Lena的眼睛、头发、帽子的边缘轮廓更加清晰。

仔细比较图4（e）和图4（f）会发现，图4（f）中可以看到柱子的部分边缘，说明实验2的方法比实验1的方法效果更好，边缘线更加突出，因为实验2中采用了原始图像两个尺度的IMF图像来重构边缘细节。

图3 实验1、实验2的结果对比Fig.3 Compariion between test 1and test 2

图4 不同方法的边缘检测结果对比Fig.4 Compariion of edge detection results to various methods

4 结 语

在传统二维EMD方法的基础上，本文在极值点的选取、边界效应的处理和SD停止准则等方面进行了改进，提出了一种易于实现的二维EMD改进方法，给出了该方法的详细实现步骤，并对Lena图像进行3层实例分解。

采用此二维EMD改进方法，先将原始图像分解获得IMF分量和余量图像，提取出IMF1和IMF2进行灰度二值化和形态学细化操作，来提取原图像的边缘。与传统的边缘检测结果相比较，这种检测边缘的方法可以更加有效地提取图像的边缘信息。基于此二维EMD改进方法的图像边缘检测可以作为图像的一个预处理步骤，为下一步的图像分割、图像识别等做好充分的准备工作。

[1]常 青.数字图像处理教程 [M].上海：华东理工大学出版社，2009.

[2]Norden E.Huang，Zheng Shen，Steven R Long，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time analysis[C]／／Proceedings of the Royal Society of Longdon，Series A ，1998，454：903-995.

[3]Nunes J C，Bouaoune Y，Delechelle E，et al.Image analysis by bidimensional empirical mode decomposition[J].Image and Vision Computing，2003，21（12）：1019-1026.

[4]Nunes J C，Guyot S，Delechelle E.Texture analysis based on local analysis of the Bidimensional Empirical Mode Decomposition [J].Machine Vision and Applications，2005，16（3）：177-188.

[5]刘忠轩，彭思龙.方向EMD分解与其在纹理分割中的应用 [J].中国科学：E辑，2005，35（2）：113-123.

[6]梁灵飞，平子良.基于窗口经验模式分解的医学图像增强 [J].Journal of Optoelectronics，Laser，2010，21（9）：1421-1425.

[7]万 建，任龙涛，赵春晖.二维EMD应用在图像边缘特征提取中的仿真研究 [J].系统仿真学报，2009，21（3）：799-801，821.

[8]胡晓辉，张晓颖，陈俊莲.一种融合小波变换和数学形态学的图像边缘检测算法 [J].铁道学报，2011，33（3）：45-48.

[9]古 昱，汪同庆.基于BEMD的Canny算子边缘检测算法 [J].计算机工程，2009，35（18）：212-213.

[10]赵春晖，任龙涛.一种基于二维EMD的图像融合方法 [J].应用科技，2009，36（9）：15-19.

[11]张 倩，占 君，陈 珊.详解 MATLAB图像函数及其应用 [M].北京：电子工业出版社，2011.