基于直接功率控制的单相AC-DC变流器控制器设计

马庆安 李群湛 邱大强 徐英雷 张丽艳

（西南交通大学电气工程学院 成都 610031）

1 引言

静止变流器大量用于变速驱动、不间断电源、光伏电池及电池储能系统等[1]。变流器的控制目标是维持直流侧电压恒定，使谐波电流含量尽量小，且功率因数接近1[2-6]。从控制角度讲，AC-DC 变流器是非线性、综合系统[6]，其控制策略值得研究。

目前已有很多控制方法用于单相变流器的控制[2-6]。滞环控制实现简单、鲁棒性强、暂态响应迅速，但开关频率不固定，造成频谱分布广泛，而恒频的滞环控制则失去了计算的简单性[7]；滑模控制响应迅速，鲁棒性强，其缺点在于确定滑模面的困难性和有限频率下的抖动性[8]；最少拍控制暂态响应迅速，但对系统参数比较敏感[9]；模糊控制缺乏有效的分析设计工具[10]；单周期控制简单、频率恒定、响应迅速，但轻载、空载时系统不稳定，而各种改进方案增加了控制系统的复杂性[11]；基于无源性网络的方法对负荷变化非常敏感[12]。文献[2]对以上几种控制方法进行了对比分析。

三相变流器直接功率控制以其结构简单、动静态特性好等优点得到了广泛研究[13-19]，然而单相AC-DC 变流器使用直接功率控制的文献非常少。文献[20]基于直接功率控制设计实现了单相变流器控制器，但内环使用了滞环电流控制方法。滞环电流控制方法开关频率不固定，造成谐波频谱分布广泛，且开关设备损耗不确定[21]。

针对以上控制方法存在的问题和缺陷，本文提出了单相电压型AC-DC 变流器的直接功率控制方法，并针对采样电压误差提出补偿措施。

2 单相AC-DC 变流器拓扑结构

单相变流器拓扑结构如图1 所示。其中，eS为单相电压源，RS、LS分别为交流侧电阻和电感，VT1～VT4为电力电子开关器件，C为直流侧电容，RL为直流侧负荷电阻，iS为交流侧电流，i为变流器直流侧输出电流，iL为直流侧负荷电流，vC为电容器电压，v为变流器两臂中点相对电压。

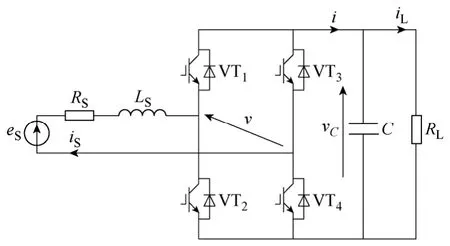
图1 单相变流器电路拓扑结构Fig.1 Diagram of full-bridge rectifier

根据图1，可列出系统状态微分方程[6]

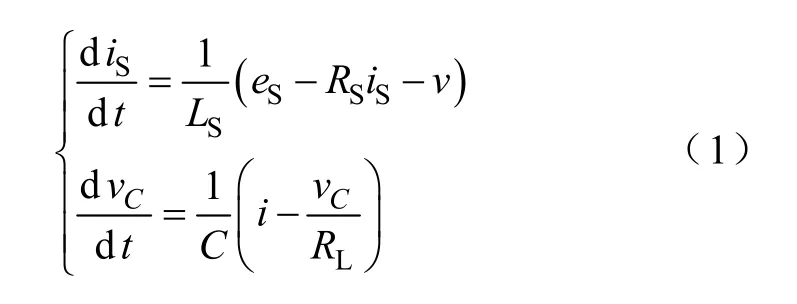
式中，eS=Emcosωt=Em，v=σvC，i=σiS，其中σ为三值逻辑开关函数，其定义为

变流器的控制目标为[6]

（2）变流器的功率因数为1，即iS=Imsinωt，其中Im为交流侧电流幅值大小。

式（1）的第2 式两边同乘以Cv，得

式中，p为变流器输出功率，Cp v i=。若不考虑变流器及交流侧电阻的功率损耗，则其应和交流侧电源的输入功率相等。由此可见，通过控制交流侧输入功率，可以直接控制直流侧电压维持在给定值。

3 dq 坐标系模型

为便于分析，将实际单相电路记为α 相，另虚构一相称为β 相，其中β 相电压滞后α 相90°[22]，这样即组成αβ 两相静止坐标系，如图2 所示。

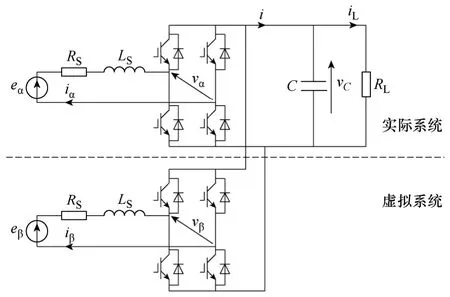
图2 实际电路和虚拟电路Fig.2 The real circuit and the imaginary circuit

不计交流侧电阻，有

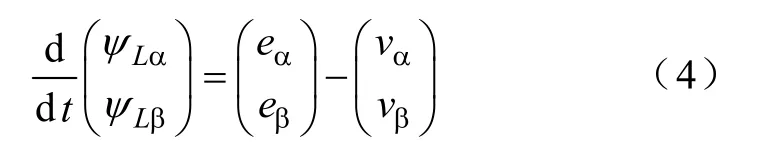
式中，ψLα，ψLβ为α相、β相电感磁链。将式（4）的第2 式乘以j 并加到第1 式，得

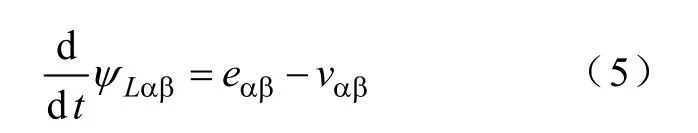
式中，ψLαβ=ψLα+jψLβ，eαβ=eα+jeβ，vαβ=vα+jvβ。

将式（5）中各复变量乘以 e-jθ，得dq 旋转坐标系下各复变量的方程

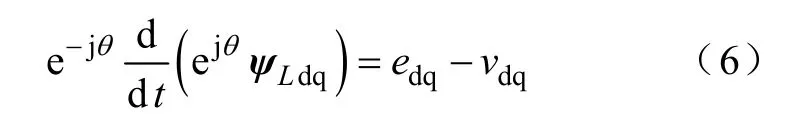
式中，θ为d 轴超前α轴的角度，。

若以eαβ对应的矢量方向作为d 轴，以超前其90°作为q 轴，有

由式（6）可得

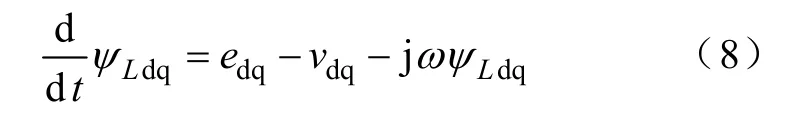
对式（8）在一个采样周期内积分

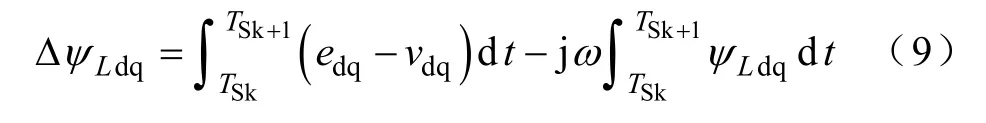
式中，TSk为采样时刻。

假设在一个采样周期内vdq、edq均保持不变，对式（9）最后一项采用梯形积分，得

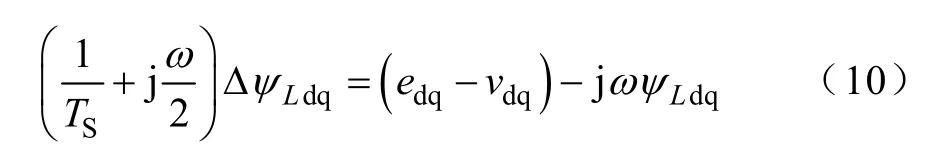
式（10）中各变量均乘以 ejθ变换到αβ 坐标系下并整理得

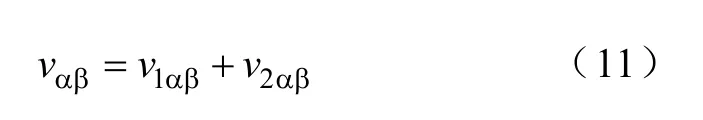
dq 坐标下瞬时复功率可定义为

考虑到式（7），得

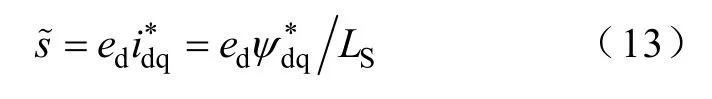
不考虑电源电压变化，则功率增量可表示为

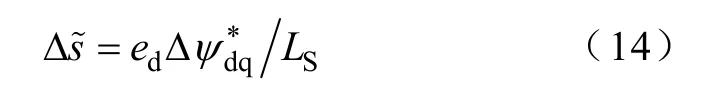
由此可见，通过控制各相电感磁链的增量即可控制有功功率和无功功率的增量，从而

由式（11），得

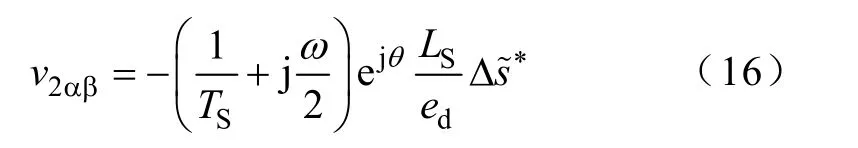
4 相位补偿

考虑到式（11）的计算是基于采样周期初始时刻的采样数据，然而由于在实现过程中，电源电压eαβ一直在发生变化，如果使用采样周期初始时刻的采样数据进行计算而不对v1αβ、v2αβ修正，将会影响系统性能，特别是在开关频率较小时。下面分别对这两部分做修正。

4.1 v1αβ的相位补偿

由式（11）可知，复功率误差为零时v2αβ=0，v1αβ=eαβ-jωψLαβ为vαβ中的稳态分量。各矢量关系如 图3a 所示。在一个采样周期当eαβ旋转到位置时，v1αβ应旋转到。在整个采样周期认为保持不 变的vC1αβ等于两者的平均值应更合适，相当于使用梯形积分，故将v1αβ修正为

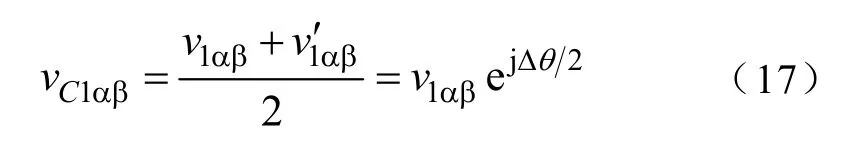
式中，Δθ为一个采样周期矢量旋转的角度。

4.2 v2αβ的相位补偿

同理，分量v2αβ也应随eαβ而变化，如图3b 所示。当eαβ旋转到位置时，v2αβ应旋转到。同理，将vC2αβ修正为

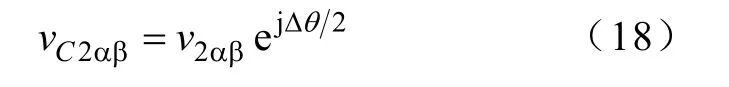
4.3 相位补偿后的vαβ表达式

如上所述，考虑了相位补偿后的vαβ可表示为

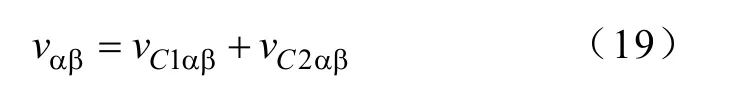
式中

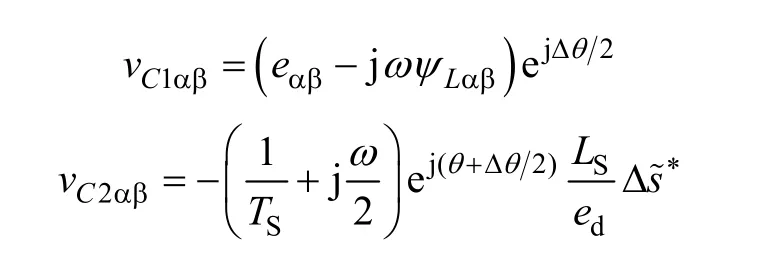
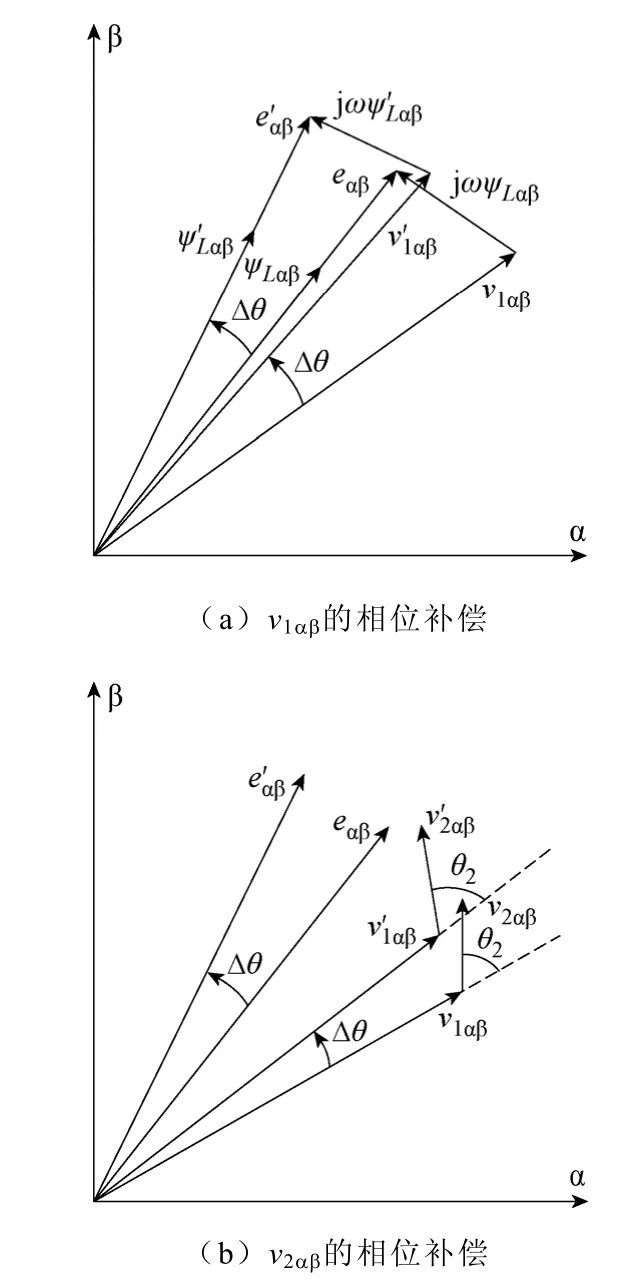
图3 变流器电压分量的相位补偿Fig.3 The compensation of voltage phasor of the converter

5 控制系统设计

5.1 功率内环控制

因vβ所对应的β相并不存在，需舍弃。

PWM 调制方式分为单极性调制方式和双极性调制方式。因单极性调制方式在同样的开关频率下交流侧谐波电流水平更低[23]，因此本文选取单极性调制方式。

将由电压外环决定的复功率与实测复功率相减，按式（11）和式（16）调节变流器交流侧电压，即可实现内环的直接功率控制。

5.2 电压外环控制——二自由度PID 控制（two-degree-of-freedom PID controller）

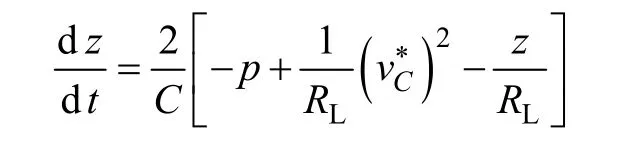
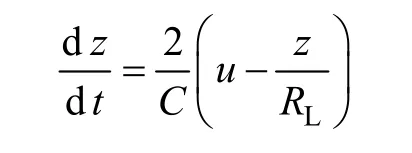
则该系统对应的传递函数为

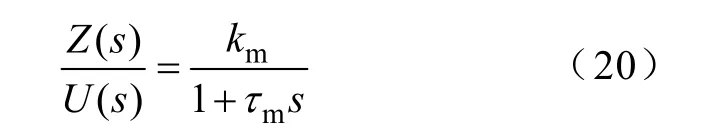
传统PID 控制器因结构简单和性价比高而得到广泛应用[24]，然而其在抗干扰能力和系统启动性能方面难以同时达到最好，因此二自由度PID 控制器（2DOF PID Controller）得到大量研究[24]。文献[25]提出一种前馈式的2DOF PI 控制器，其结构如图4所示。该控制器能满足系统需要的鲁棒性和闭环响应速度，同时降低启动过程的超调量。图4 中，G(s)为被控对象传递函数，Gy(s)为反馈控制器，Gr(s)为前馈控制器。

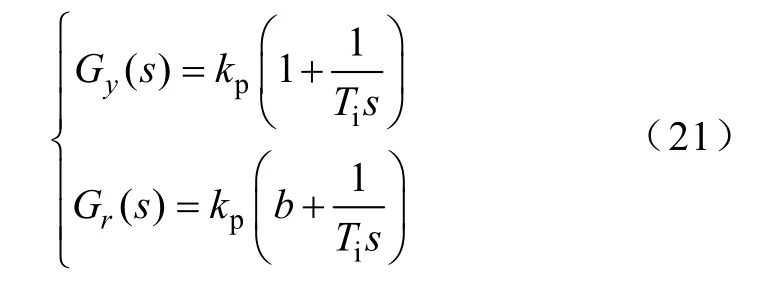
式中，b为调节系数，0＜b＜1。在实现时可将Gy(s)后移与G(s)串联，这时前馈控制器为，即超前滞后环节。

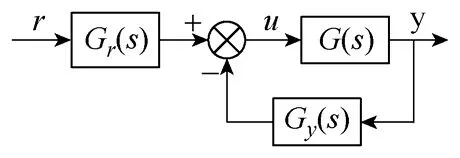
图4 2DOF PI 控制器结构Fig.4 2DOF PI controller configuration

若电力电子开关器件的开关频率足够高，在设计电压环控制器时，可认为实际变流器功率能完全跟踪指定功率变化。

根据系统鲁棒性要求可设定系统最大灵敏度Ms。

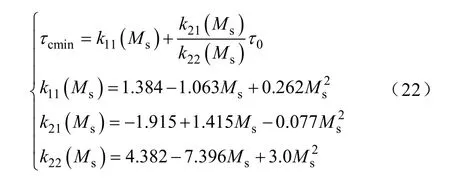
由式（22）[25]可确定闭环系统时间常数与被控对象时间常数之比τc的最小值τcmin。

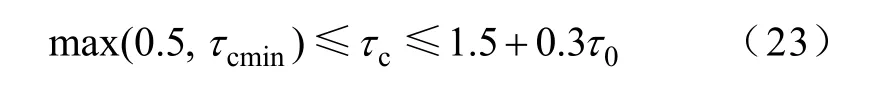
式中，τ0为被控对象延迟时间与时间常数之比。再根据式（23）[25]选择τc。由于要求系统响应迅速，可选择τc=max(0.5,τcmin)。由此可确定Gy(s)，从而可根据确定b的值。b=1 对应传统PI 控制器。

控制系统结构如图5 所示。

6 仿真分析

为验证方法的正确性，本节基于PSCAD/EMTDC 进行了仿真分析。系统参数为[3]：开关频率20kHz。计算得km=100，τm=0.11s，τ0=0s。考虑到负荷可能发生较大变化，本文选择最大灵敏度Ms=1.4，由式（22）可确定τcmin=0.409 3，由式（23）选择τc=0.5，计算可得电压外环PI 控制器比例系数kp=0.03，时间常数τI=0.082 5s，b=0.667。

在额定负载下，b=0.667 时，系统启动过程中电容器电压响应曲线如图6a 所示，b=1 时电容器电压响应曲线如图6b 所示。由此可见，b=1 时电容器电压有明显的超调现象发生，最大值达到237.6V，超调量18.8%；而b=0.667 时基本没有超调现象发生。

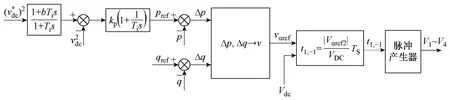
图5 DPC 控制系统结构图Fig.5 Diagram of DPC control

为研究抗负荷扰动的能力，设t=0.5s 时负荷电阻RL由100Ω 跃变为20Ω，电容器电压响应如图6所示。由图6 可见，电容器电压下降到约162V，经过约0.1s，vC重新到达稳定状态。

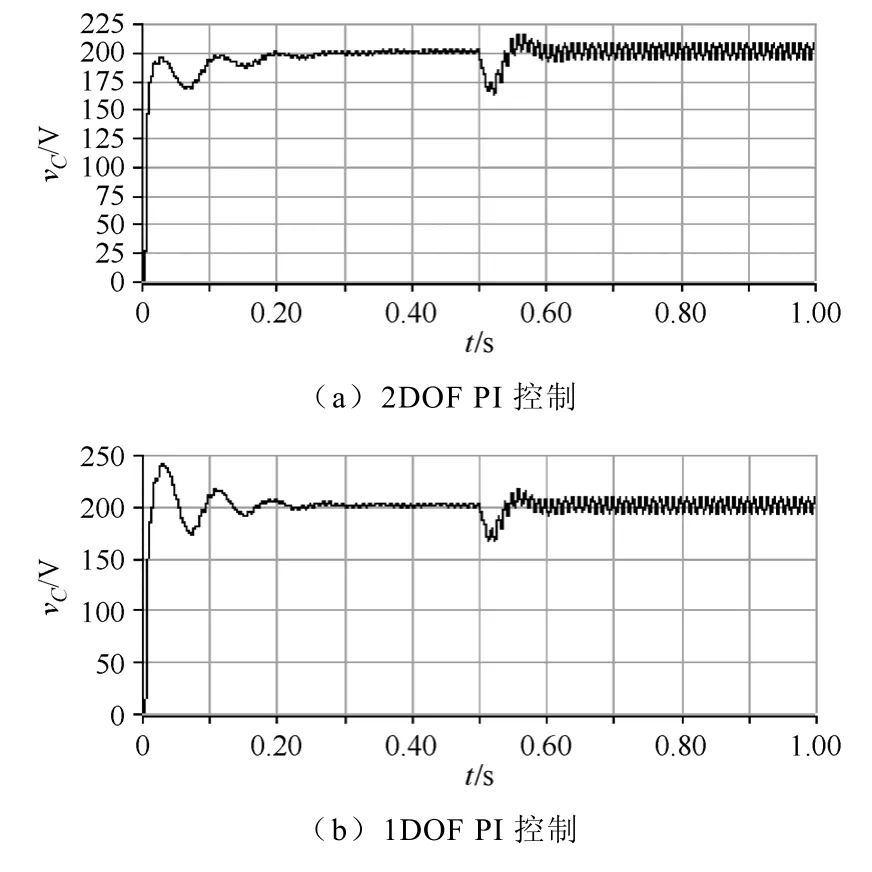
图6 电压vC 上升曲线Fig.6 Curves of vC under various conditions

从图7 可见，稳态时直流侧电压波动和负荷有关。负荷功率越大，直流侧电压波动越剧烈。

由于前馈环节只对启动过程有影响，因此b为何值对稳态波形没有影响。额定负载下系统电压eS和电流iS如图7 所示，其中电流放大了10 倍。图8为αβ 二相系统的瞬时有功、无功功率。由图可见，系统吸收的无功功率为零，因此系统交流侧功率因数接近1。额定负载下电流iS对应的谐波含量如图9，其中基波为1，3 次谐波电流含量最大，为0.017。由于开关频率非常高，还会有更高次谐波出现，本文未示出。

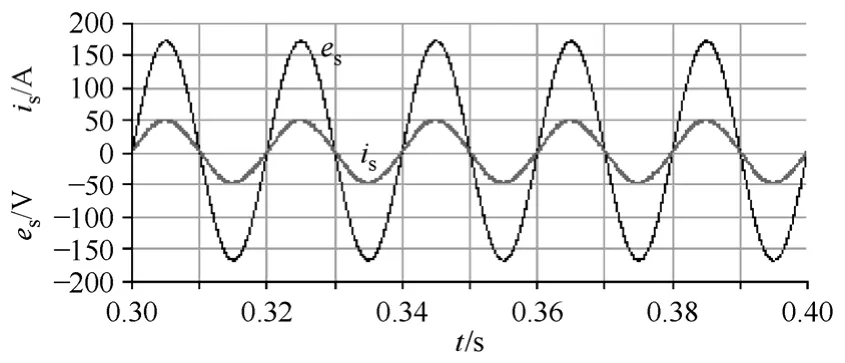
图7 额定负载时系统交流侧电压和电流Fig.7 Waveforms of AC-side voltage and current

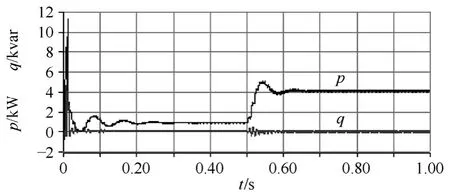
图8 αβ 二相系统交流侧有功和无功功率Fig.8 Active and reactive power absorbed by the αβ system

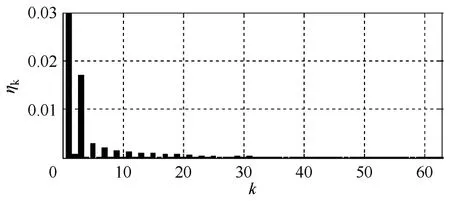
图9 交流侧电流频谱Fig.9 Spectrum of AC-side current

7 结论

本文提出了AC-DC 单相变流器的直接功率控制方法。功率内环根据功率误差调节变流器交流侧电压，电压外环采用的二自由度PI 控制器能在满足鲁棒性要求的同时降低启动过程的超调量，实现了谐波含量小和接近单位功率因数的要求。基于PSCAD/EMTDC的仿真结果验证了方案的可行性。

[1]Singh B,Singh B N,Chandra A,et al.A review of single-phase improved power quality AC-DC converters[J].IEEE Transactions on Industrial Electronics,2003,50(5):962-981.

[2]Karagiannis D,Mendes E,Astolfi A,et al.An experimental comparison of several PWM controllers for a single-phase AC-DC converter[J].IEEE Transactions on Control Systems Technology,2003,11(6):940-947.

[3]Gaviria C,Fossas E,Grino R.Robust controller for a full-bridge rectifier using the IDA approach and GSSA modeling[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2005,52(3):609-616.

[4]Escobar G,Chevreau D,Ortega R,et al.An adaptive passivity-based controller for a unity power factor rectifier[J].IEEE Transactions on Control Systems Technology,2001,9(4):637-644.

[5]Dong D.Modeling and control design of a bidirectional PWM converter for single-phase energy systems[D].Blacksburg,VA:Virginia Polytechnic Institute and State University,2009.

[6]Giri F,Abouloifa A,Lachkar I,et al.Formal framework for nonlinear control of PWM AC/DC boost rectifiers—controller design and average performance analysis[J].IEEE Transactions on Control Systems Technology,2010,18(2):323-335.

[7]Kazmierkowski M P,Malesani L,Current control techniques for three-phase voltage-source PWM converters:a survey[J].IEEE Transactions on Industrial Electronics,1998,45(5):691-703.

[8]Khalil H K.Nonlinear Systems[M].3rd Edition.Beijing:Publishing House of Electronics Industry,2007.

[9]Su Chen,Joos G.A disturbance predictive deadbeat control for unified series-parallel power quality compensators[C].2004 IEEE 35th Annual Power Electronics Specialists Conference,2004,2:1180-1186.

[10]Maidi A,Diaf M,Corriou J P.Optimal linear PI fuzzy controller design of a heat exchanger[J].Chemical Engineering and Processing,2008,47(5):938-945.

[11]Ghodke D V,Chatterjee K,Fernandes B G.Modified one-cycle controlled bidirectional high-power-factor AC-to-DC converter[J].IEEE Transactions on Industrial Electronics,2008,55(6):2459-2472.

[12]Jeltsema D,Scherpen J M A.Tuning of passivity-preserving controllers for switched-mode power converters[J].IEEE Transactions on Automatic Control,2004,49(8):1333-1344.

[13]王久和,李华德,王立明.电压型PWM 整流器直接功率控制系统[J].中国电机工程学报,2006,26(18):54-60.Wang Jiuhe,Li Huade,Wang Liming.Direct power control system of three phase boost type pwm rectifiers[J].Proceedings of the CSEE,2006,26(18):54-60.

[14]Hadian Amrei S R,徐殿国,郎永强.一种PWM 整流器直接功率控制方法(英文)[J].中国电机工程学报,2007,27(25):78-84.Hadian Amrei S R,Xu Dianguo,Lang Yongqiang.A new direct power control for PWM rectifier[J].Proceedings of the CSEE,2007,27(25):78-84.

[15]陈伟,邹旭东,唐健,等.三相电压型PWM 整流器直接功率控制调制机制[J].中国电机工程学报,2010,30(3):35-41.Chen Wei,Zou Xudong,Tang Jian,et al.DPC modulation mechanism of three-phase voltage source PWM rectifiers[J].Proceedings of the CSEE,2010,30(3):35-41.

[16]Vazquez S,Sanchez J A,Carrasco J M,et al.A model-based direct power control for three-phase power converters[J].IEEE Transactions on Industrial Electronics,2008 ,55(4):1647-1657.

[17]Bouafia A,Krim F,Gaubert J P.Fuzzy-logic-based switching state selection for direct power control of three-phase PWM rectifier[J].IEEE Transactions on Industrial Electronics,2009,56(6):1984-1992.

[18]Restrepo J A,Aller J M,Viola J C,et al.Optimum space vector computation technique for direct power control[J].IEEE Transactions on Power Electronics,2009,24(6):1637-1645.

[19]Zhi Dawei,Xu Lie,Williams B W.Improved direct power control of grid-connected DC/AC converters[J].IEEE Transactions on Power Electronics,2009,24(5):1280-1292.

[20]Azab M.A new direct power control of single phase PWM boost converter[C].IEEE 46th Midwest Symposium on Circuits and Systems,2003,3:1081-1084.

[21]Rodriguez Jos,Pontt Jorge,Silva C A,et al.Predictive current control of a voltage source inverter[J].IEEE Transactions on Industrial Electronics,2007,54(1):495-503.

[22]Zhang R,Cardinal M,Szczesny P,et al.A grid simulator with control of single-phase power converters in D-Q rotating frame[C].IEEE 33rd Annual Power Electronics Specialists Conference,2002,3:1431-1436.

[23]Mohan N,Undeland T,Robbins W.Power electronics:converters,applications,and design[M].2nd Ed.New York:John Wiley & Sons,Inc.,1995.

[24]Araki M,Taguchi H.Tutorial paper:two-degree-of-freedom PID controllers[J].International Journal of Control,Automation,and Systems,2003,1(4):401-411.

[25]Alfaro V M,Vilanova R,Arrieta O.Analytical robust tuning of PI controllers for first-order-plus-dead-time processes[C].IEEE International Conference on Emerging Technologies and Factory Automation,2008:273-280.