基于累积指数的电网电压稳定性能的评估
2012-07-06张学清董晓明
张学清 梁 军 董晓明
(山东大学电气工程学院 济南 250061)
1 引言
随着人类生活水平的不断提高以及社会经济的持续快速发展,负荷需求种类和数量也不断地增加;同时电网规模的不断扩大以及特高压交直流的广泛
接入,都给电网稳定与控制带来了新的挑战,而如何有效地保持电网的电压稳定已经成为电网运行与监控的关键问题[1]。
传统电压稳定性分析主要是利用稳态代数方程的理论,如戴维南等值法[2,3]、连续潮流法[4,5]、灵敏度分析法[6]和模态分析法[7]等。传统分析方法由于未考虑电网的动态变化过程,尤其是电源与负荷的动态特性,所以有必要考虑电网的动态特性进行电压稳定性能的评估[8]。近年来,信号能量法已经在机械、动力[9]工程领域得到了广泛的应用。文献[10]提出了暂态电压响应的信号能量,能随着功率的增加而渐进的增长,并建立了信号能量与传输功率和稳定极限的解析函数关系。文献[11]提出一种基于轨迹识别系统主导振荡模式的信号能量法,可应用识别多机系统的主要振荡模式,取得了较好效果。目前在确定地区电网电压稳定的薄弱节点的研究中考虑过渡过程特性的应用提及较少,并且在现有的网架结构下确定地区电网的电压薄弱节点对于指导电网的运行和规划具有一定的意义。
本文提出了一种基于累积指数的电网稳定性能评估的方法。该方法首先利用PSSE的仿真功能得到电网各节点负荷受扰的电压幅值的信息,由此得出分时段的信号能量谱信息。在此基础上利用动力学的波动强度理论选取了最佳信号能量波动序列的长度;然后通过构造累积指数判据,确定电网中电压稳定的薄弱节点。为验证本文所提方法的可信性,利用传统电压分析理论中的PV 曲线法、戴维南等效法[2,12]和本文方法,以山东电网2010年冬的系统运行数据为算例进行对比分析,验证本文方法的有效性。
2 理论基础
2.1 分时段信号能量定义
文献[13]指出,利用系统的时域仿真结果可以提取出在选定母线下的暂态电压响应信号。由于传统的基于能量谱的方法没有考虑到各个负荷节点电压信号能量沿时间轴的分布特点,有可能导致提取的特征参数不能准确反映暂态信号的特征,所以有必要研究分时段的能量谱理论,分时段能量谱可定义为
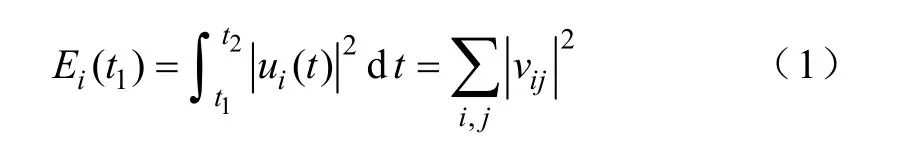
式中,E i(t1)为第i条母线t1时段的信号能量;vij(i=1,…,n;j=1… ,k)为暂态仿真选定第i母线第j时段的电压幅值。
2.2 波动强度
波动强度[14](fluctuation intensity)是应用于动力学领域的一种统计物理概念。可以表征信息序列曲线的波动程度,某一段序列波动强度越小,信号波动越小,否则波动越剧烈。
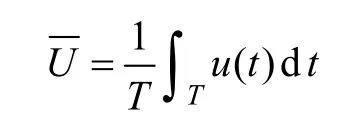
则波动强度数学表达式为

式中,ε表示为波动强度;n为序列的点数;T为采样周期;u(t)为序列各点值;为这段序列的平均值。
累积指数(cumulating index)是在稳定性理论的超调量和调节时间的思想的指导下利用分时段的信号能量谱概念而得出的,超调量越小、调节时间越短即系统各个负荷节点接受相同的扰动后能恢复稳态的时间越小,那么这个负荷节点也越容易稳定,即此负荷节点稳定性能越好,属于强节点,反之为弱节点。下面以经典二阶系统稳定理论为例说明累积指数方法的有效性。
2.3 经典二阶系统阶跃响应信号分析
由经典稳定性理论知,系统的稳定性主要由系统特征根的实部决定,而且特征根的实部离虚轴越远,则所代表的系统更稳定。本文以三个典型的二阶系统受到单位阶跃响应为例,验证本文所提方法的有效性,响应曲线如图1 所示。
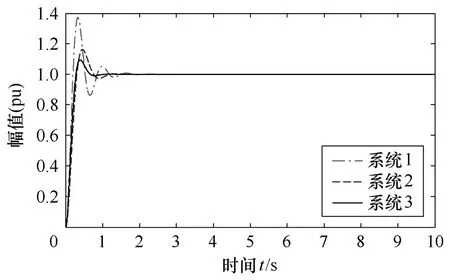
图1 典型二阶系统的阶跃响应曲线Fig.1 Typical curve of second-order system step response
由图1 易见系统3 比系统1 和2 稳定。各系统特征根及累积指数见表1。由表1 知,因为系统3特征根的实部比系统1 和2的实部离虚轴更远,所以系统3 更稳定。通过系统的超调量和调节时间等性能指标进行对比分析,显然系统3的超调量和调节时间都大于系统1 和2,由此说明系统3 比系统1和2 稳定。

表1 各系统特征根以及累积指数Tab.1 Eigenvalues and cumulating index of each system
3 累积指数
本文采用分时段能量谱概念,考虑波动强度理论的基础上给出累积指数(CI)的概念,定义如下
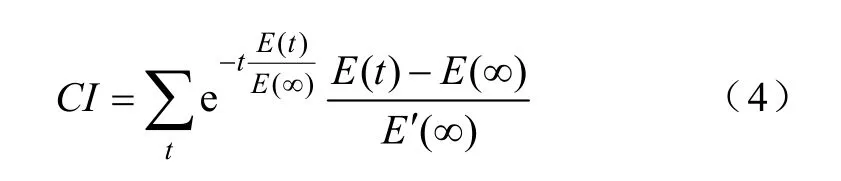
式中,t为仿真的时段;E(t)为第t时间段的信号能量;E′(∞)为受扰信号经过波动强度理论判定为平稳后的时段信号能量;E′(∞)为受扰信号未处理前平稳后的稳态信号能量,如果不经处理,E′(∞)=E(∞)。
累积指数体现了系统超调量和调节时间性能指标的关系,也体现了信号随时间变化的特征。当系统失稳或者临界振荡时,E′(∞)和E′(∞)为零,通过对式(4)求极限易得此极限为无穷大;如果经过一段时间系统平稳,通过计算分析则其有确定的数值,且累积指数越小,稳定性能越好。如果没有指数部分,将不能体现调节时间的指标思想。其可从整体上反映系统各部分综合作用的结果[15],体现了系统自身的性质。
以系统1、2 和3 为例,用累积指数分析如下:从图1 可以看出,系统1 调节时间比系统2 和3 明显变长,而且用累积指数计算得出的数值,-0.002 685 9明显大于-0.039 736 和-0.043 246。这里指数出现了负值,是因为第1 时段与最后的时段的信号能量相比较小,所以出现了负值,但是并不影响累积指数法的成立。但是在电力系统的应用中累积指数很少会出现负值,这是因为随着扰动过程的持续,系统在各种调节装置包括发电机、励磁系统、调速系统以及各种补偿装置等共同的作用下,接近平稳时段的信号能量明显小于开始受扰瞬间的信号能量,因此,电力系统中基本不会出现指数非负的情况,这从后续分析中可以看出。所以系统1 比系统2 和3稳定性能差,也验证了累积指数能很好地区分系统的稳定性能的强弱。
对于电力系统来说,通常需要确定电网中的薄弱节点,以利于调度部门对该节点进行重点监控。鉴于此,把累积指数引入到确定电网薄弱节点的分析中,计算电网各个节点的累积指数的大小,累积指数越小,说明此节点的稳定性能越好,如果经受同样比例的扰动,发生电压失稳如临界振荡,通过对式(4)求极限易得到无穷大,说明已经失稳。且累积指数确定的指标能随扰动大小的不同而不发生变化,所以累积指数能用于评估电力系统节点电压稳定性能的强弱。
4 算例分析
本文以山东电网2010年冬季孤网运行方式为例验证本文方法的有效性。2010年冬季,山东电网由河北辛安站以及廉州站,受电4 000MW。宁东直流单极运行(胶东站)受电2 000MW。
4.1 算例仿真
在山东电网2010年冬季孤网运行方式下,用山东电网整个大区域作为本文算例。为了节约篇幅,以山东潍坊受电区域的节点结果展示为例,运用累积指数法确定电网的薄弱节点。部分受电区域图如图2 所示。
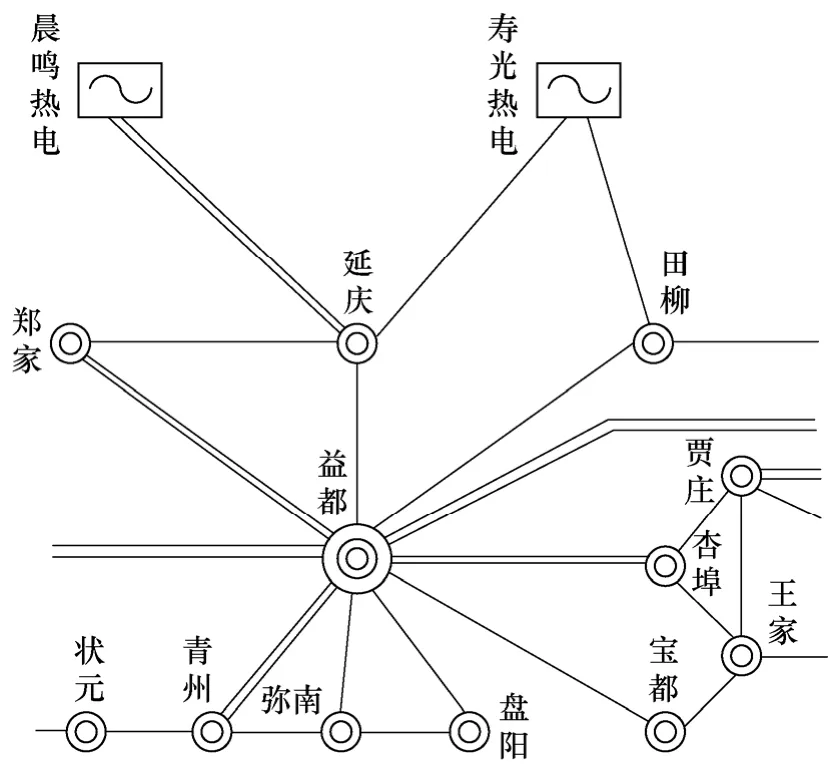
图2 山东电网潍坊受电区域图Fig.2 Electrical map of Weifang in Shandong grid
图2 中潍坊地区11 个负荷节点都用三绕组变压器与输电系统关联,其中三绕变模型的220kV 侧接输电线路,110kV 侧接等效负荷,35kV 侧接补偿装置。以原山东电网全网各负荷节点的功率因数增冲击负荷,在PSSE 中仿真了山东电网各个负荷节点的电压幅值变化情况。本文首先利用PSSE的潮流计算模块FNSL 计算了山东电网的各节点的电压幅值和相角,并以此为基础利用PSSE的STRT,RUN等模块仿真了山东电网各个节点的电压变化情况。发电机采用的是PSSE的经典5 阶模型GENSAL,励磁模型采用的是自定义模型,调速系统采用了PSSE的IEEEG1 模型,负荷模型采用的是PSSE的综合负荷CLOD 模型,直流输电部分采用CDC6T模型。仿真的具体情况是从0 开始仿真各个负荷节点的电压幅值,运行到1s 时,突然全网按照各节点的功率因数增1%的冲击有功和无功负荷,运行到4s 时再按照全网各节点的功率因数增2%的冲击有功和无功负荷,仿真到第29s 结束。潍坊地区的部分220kV 负荷节点的电压幅值变化情况如图3 所示。
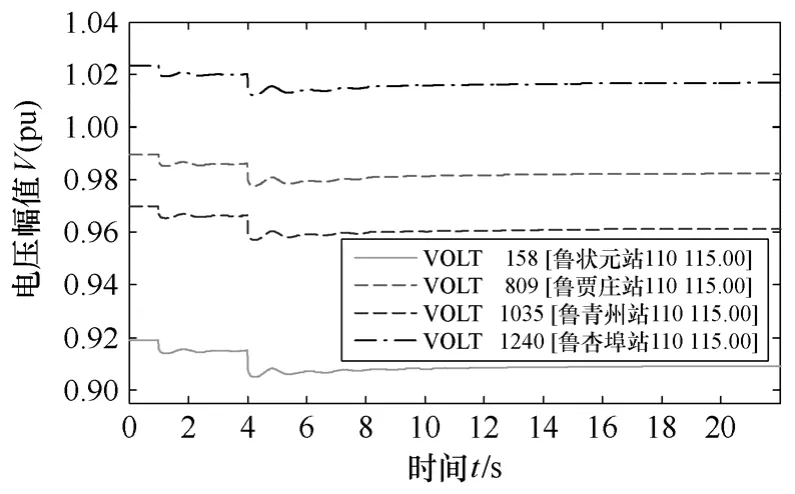
图3 潍坊受电区域部分负荷节点的电压幅值变化曲线Fig.3 Voltage magnitude curve of load node in Weifang zone
应用暂态信号判断系统各个节点的电压稳定程度的强弱,常规的方法是利用各负荷节点的电压初值以及受扰过程中电压跌落的最小值来判断节点受扰的强弱。这种方法是有局限性的,其没有考虑受扰之后相当长时间内信号的变化情况以及受扰恢复之后的电压变化情况,而累积指数方法则综合考虑了这些因素。为了应用累积指数,本文进行了如下的处理。由于各个负荷节点初始电压各不相同,而且受扰之后达到稳态时电压幅值也不相同,本文将各个负荷节点的电压初始情况统一归算到相同的电压初始值,即对每一个负荷节点的电压幅值向量减去它们的初始值电压幅值组成的向量,并且第一个时段就是从最后一个受扰开始时刻即仿真的第4s 开始的,其后依此类推,其中式(4)中分母的稳态时段能量仍采用归算前表示形式并除以1 000,这样可以保证如果某一节点发生电压失稳,稳态能量为零,指数为无穷大表明系统失稳。潍坊地区部分负荷节点前10 个时段信号能量见表2。
4.2 最佳信号序列长度的确定
确定电网各个节点的电压稳定程度的强弱,首先需要确定最佳波动序列的长度。前面提到的波动强度理论可以表征信号序列波动程度,所以通过对仿真得到的全网各节点按各自的功率因数递增相同的有功和无功负荷的电压幅值波动曲线分别计算每一时段的波动强度值,再把该区域中的所有负荷节点的波动强度数值用曲线联系起来,得到如图4 所示的各负荷节点的波动强度。从图3 可以看到,所有的负荷节点的波动强度曲线在第17 个时段基本维持平稳,即到第17 个时段时的信号序列已能很好地表征信号的主要特征,为计算方便这里将第 21个时段以前的序列作为本文分析电压波动信号,这样能保证不遗漏有用的信息。
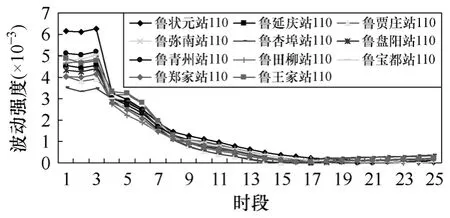
图4 潍坊受电区域各负荷节点的波动强度变化曲线Fig.4 Fluctuation intensity curve of load node in Weifang
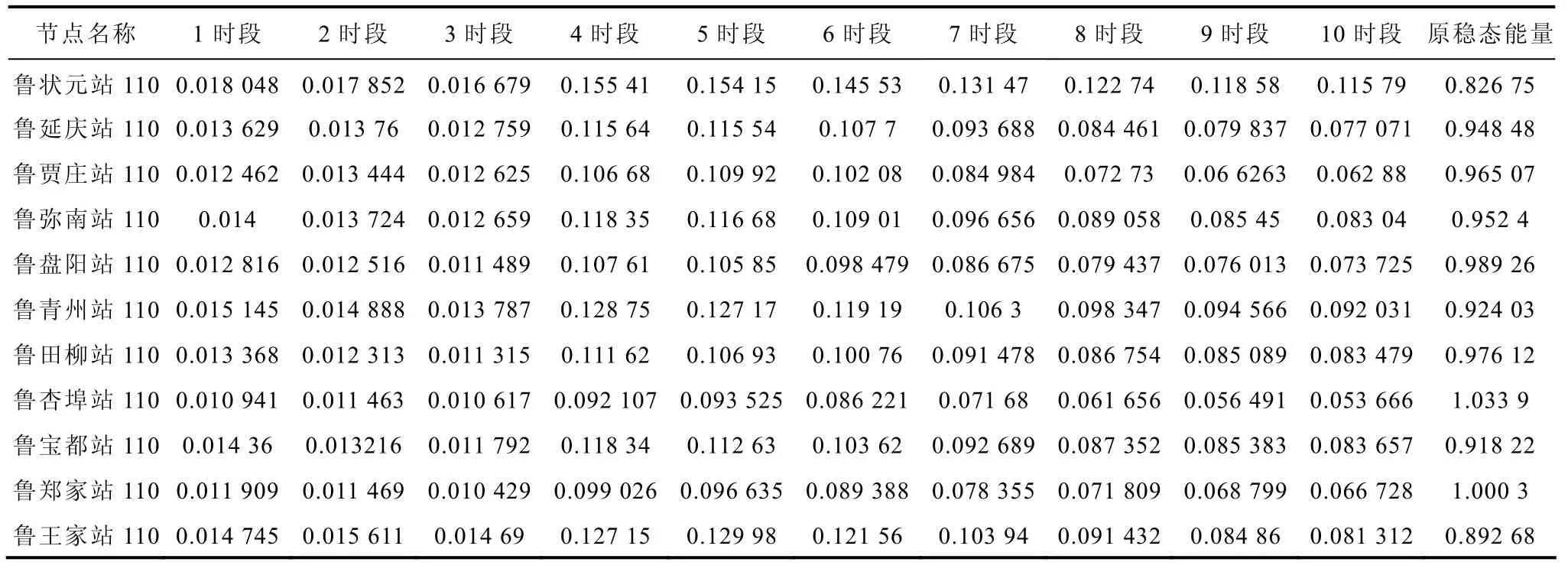
表2 潍坊地区负荷节点的各时段信号能量Tab.2 Signal energy of each time for load node in Weifang
各个负荷节点的累积指数数值见表3。从表3可见,潍坊地区鲁状元110kV 站指数最大,所以此负荷节点电压稳定性能较差,为此区域的薄弱节点,而此地区的鲁杏埠110 站指数最小,所以此负荷节点电压稳定能较好,为此受电区域的强节点。本文还仿真了另一组负荷扰动即从0 开始仿真各个负荷节点的电压幅值,运行到1s 时,突然全网按照各节点的功率因数增2%的冲击有功和无功负荷,运行到4s 时再按照全网各节点的功率因数增4%的冲击有功和无功负荷,仿真到第29s 结束。潍坊地区的220kV 部分负荷节点的累积指数数值见表4。通过表4 可见,薄弱节点仍是状元站和青州站,指数数值相对较大,而强节点仍是贾庄110 站和杏埠110站,指数数值相对较小。而且表4的排列顺序与表3 完全一致,说明由累积指数确定的节点电压稳定性能评估排序结果不随扰动的大小而变化,具有很好的一致性,且说明负荷节点稳定性能的强弱不因扰动大小而变化,而是由系统本身的结构决定的,即全网各部分包括网架结构和控制装置综合作用的结果。
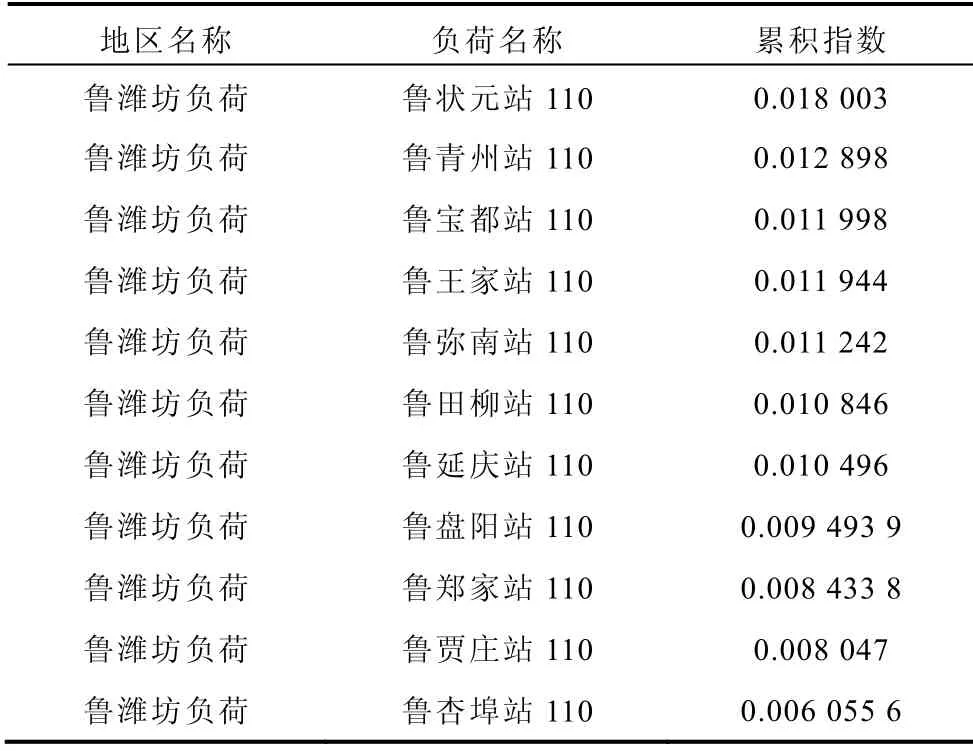
表3 潍坊地区各负荷节点累积指数Tab.3 Cumulating index of each load node in Weifang
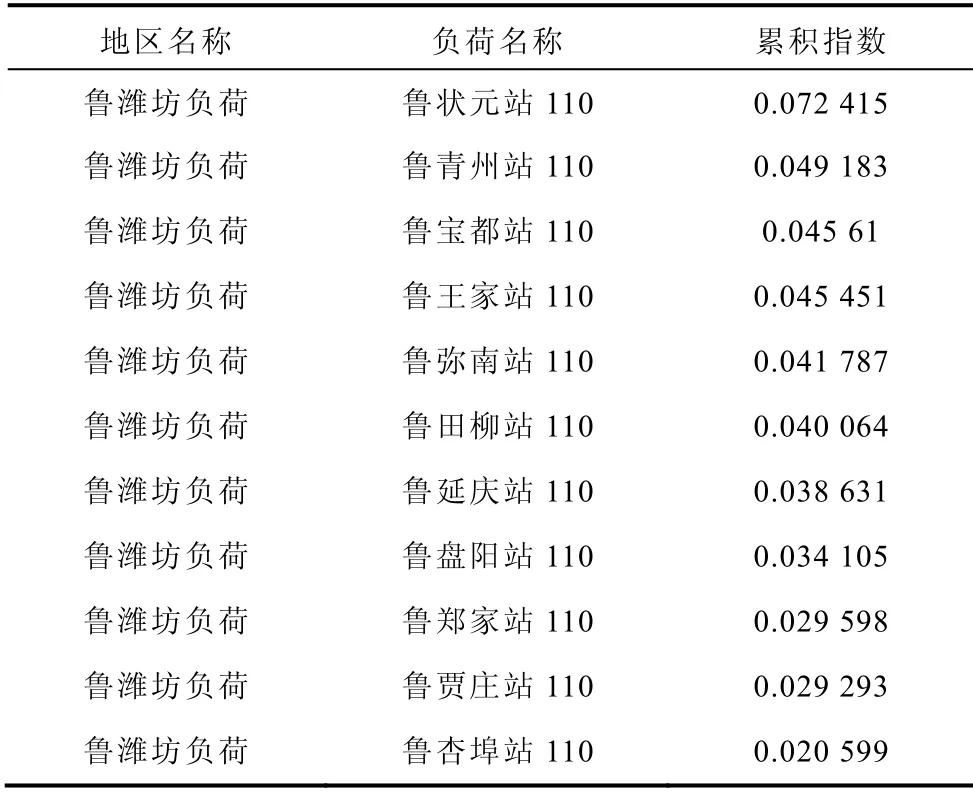
表4 潍坊地区各负荷节点累积指数Tab.4 Cumulating index of each load node in Weifang
5 传统分析方法验证
为了验证本文方法的有效性,鉴于传统分析方法应用在电压稳定分析中已经很多,在此利用传统分析方法中的PV 曲线法[4,5,8]和戴维南等效法[16-18]来验证潍坊地区的薄弱节点。
5.1 连续潮流(PV 曲线)法
设计功率增长模式为单个负荷节点保持功率因数缓慢增长,由虚拟的华北平衡机提供不平衡功率增长,直至静态电压稳定临界点。
忽略发电机出力限制、节点电压、线路热电流等约束条件,仅考察网络的极限功率输送能力。结果见表5。表中λ为临界功率与基准点功率比值。
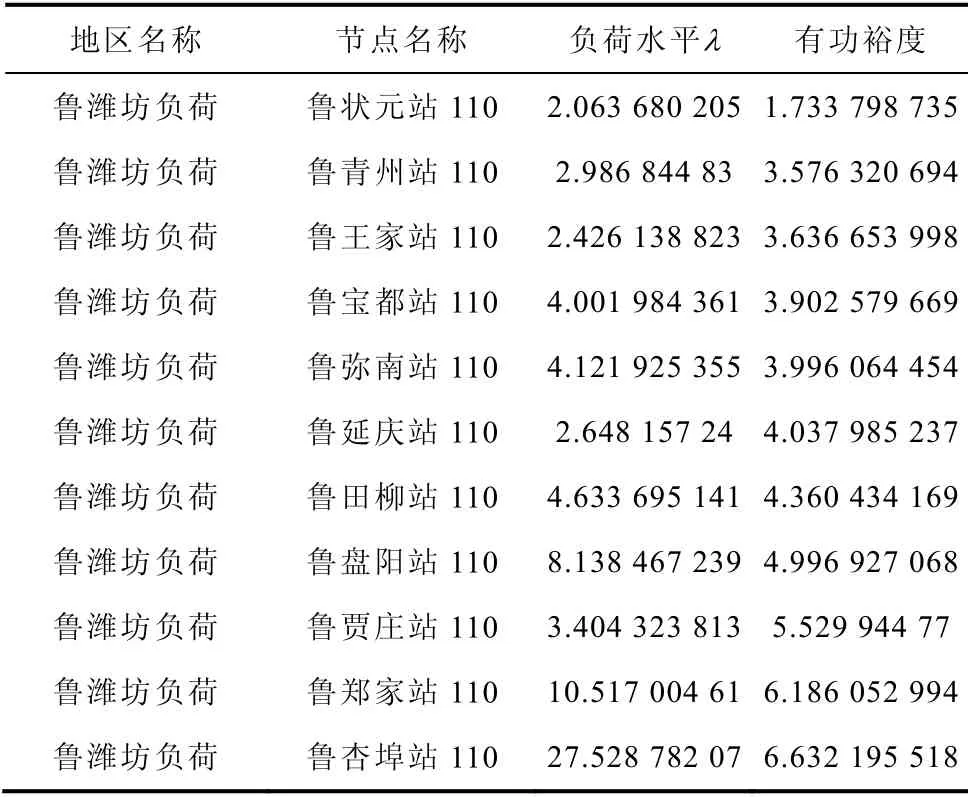
表5 负荷节点的临界电压幅值指标Tab.5 Threshold voltage amplitude index of load node
5.2 戴维南等效法
具体实现方法是,将辛安站以及廉州站统一等值为华北平衡机,作为平衡节点处理。并将直流部分等值为一台定出力发电机,以PQ 节点处理。山东电网冬季大方式下,在全网发电和负荷初始值基础上,各自功率因数递增一小的量(类似平衡点线性化处理),得到两个潮流数据断面,进而求得各节点戴维南等效参数,具体参见文献[16]。本文用到的三个指标,即阻抗指标、功率指标以及角度指标,具体见文献[3,12,18]。在以上三个指标的基础上对每一个负荷节点通过求三个指标之和的平均值得到的平均指标的概念去确定山东潍坊受电区域节点电压稳定强弱的排列顺序,结果见表6。
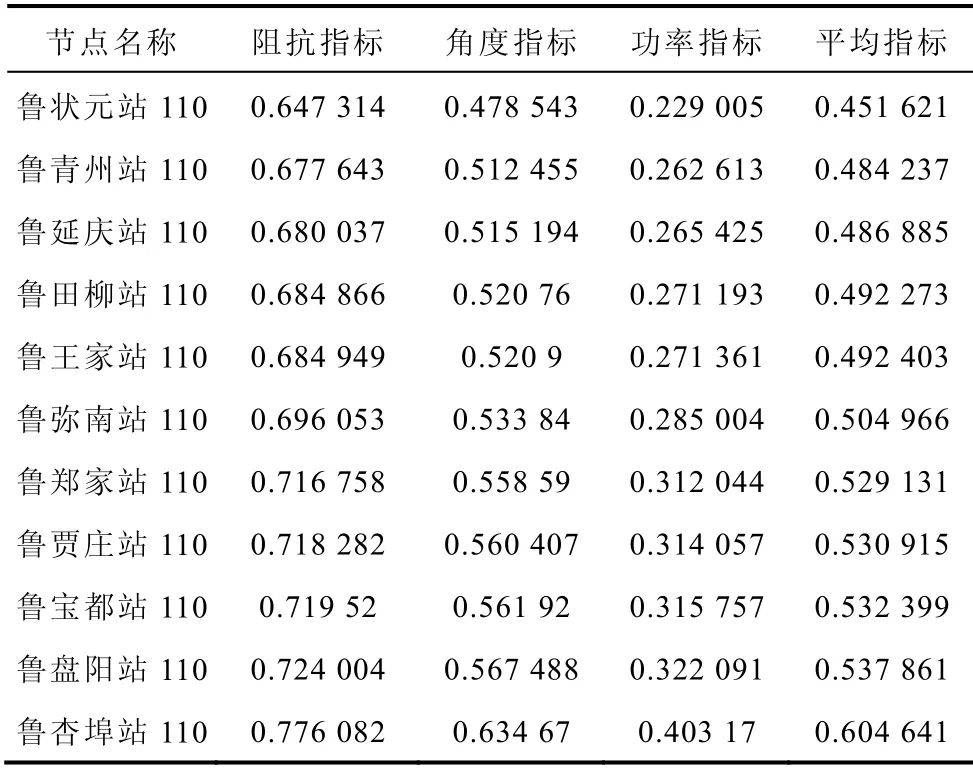
表6 负荷节点的各种裕度指标Tab.6 Each margin index of load node
对比表3、表5 和表6 可知,PV 曲线法分析结果表明状元站、青州站、王家站和宝都站都是相对弱节点,而累积指数法结果表明状元站、青州站、宝都站和王家站为弱节点,而戴维南等效法分析结果也表明状元站和青州站为较弱节点,可见传统分析方法与累积指数结果基本一致。虽然部分节点有些许差别,但是大体趋势与PV 曲线法基本一致。出现此种情况的原因是,本文考虑了发电机、励磁和调速系统、直流控制系统和各种负荷动态模型得出的结论,而传统电压分析没有考虑各种元件的详细模型,主要基于稳态的代数方程理论,没有考虑过渡过程内的变化情况;传统分析方法负荷增长是缓慢的,忽略了过渡过程中有用的快速变化信息。所以两种计算有偏差,但是大体趋势一致,就是戴维南等效法结果中杏埠站的平均指标明显大于本文累积指数计算出来薄弱节点状元站和青州站的平均指标。本文采用了冲击负荷连续扰动的形式,而没有采用直流闭锁以及短路等扰动形式就是为了分析在现有的网架结构和控制装置的作用下电网各节点的电压稳定性能的强弱。所以用传统分析方法也验证了本文方法的有效性。
6 结论
本文针对电力系统电压稳定性能评估中如何在现有的网架结构下确定电网中电压稳定薄弱节点这一问题,借鉴系统的超调量和调节时间等性能指标,在信号能量法的基础上结合分时段信号能量谱提出了累积指数法。针对山东电网2010年冬典型运行方式下用PSSE 仿真了系统按原功率因数连续增冲击负荷扰动下潍坊受电区域各负荷节点的电压幅值变化情况,并用累积指数法确定了电网的薄弱节点,并证明了累积指数确定的节点电压稳定性能评估排序结果能不随扰动的大小而变化。最后用传统电压分析法验证了本文所提方法的有效性,本方法适用于离线静态电压稳定评估,而且计算迅速,可为在现有网架结构下进行电网的运行与规划提供参考,有一定的工程意义。而利用累积指数法对薄弱节点进行稳定裕度分析的问题还有待于做进一步的深入研究。
[1]薛禹胜.时空协调的大停电防御框架(二):广域信息、实时量化分析和自适应优化控制[J].电力系统自动化,2006,30(2):1-10.Xue Yusheng.Space-time cooperative framework for defending blackouts,part Ⅱ:reliable information quantitative analyses and adaptive controls[J].Automation of Electric Power Systems,2006,30(2):1-10.
[2]柳焯.基于节点阻抗解析的电压稳定性预估[J].中国电机工程学报,1999,19(11):64-68.Liu Zhuo.Voltage stability evaluation based on node load impedance analyses[J].Proceedings of the CSEE,1999,19(11):64-68.
[3]刘道伟,韩学山,王勇,等.在线电力系统静态稳定域的研究及其应用[J].中国电机工程学报,2009,29(34):42-49.Liu Daowei,Han Xueshan,Wang Yong,et al.Studies on the on-line static stability region in power systems and its application[J].Proceedings of the CSEE,2009,29(34):42-49.
[4]赵晋泉,黄文英,方朝雄,等.福建电网在线电压稳定监视与控制系统(VSMC)[J].电力系统自动化,2007,31(14):102-106.Zhao Jinquan,Huang Wenying,Fang Zhaoxiong,et al.Fujian on-line voltage stability monitoring and control system[J].Automation of Electric Power System,2007,31(14):102-106.
[5]赵晋泉,王毅,李可文,等.一种基于连续潮流的在线静态稳定综合评估方法[J].电力系统自动化,2010,34(4):18-22.Zhao Jinquan,Wang Yi,Li Kewen,et al.An on-line voltage stability composite assessment method based on continuation power flow[J].Automation of Electric Power Systems,2010,34(4):18-22.
[6]段献忠,何仰赞,陈德树.论电力系统电压稳定几种实用判据和安全指标[J].电力系统自动化,1994,18(9):36-41.Duan Xianzhong,He Yangzan,Chen Deshu.On some practical criteria and security indices for voltage stability in electric power system[J].Automation of Electric Power Systems,1994,18(9):36-41.
[7]Taylor C W.Power System Voltage Stability[M].New York:McGraw-Hill,1994.
[8]王锡凡,方万良,杜正春.现代电力系统[M].北京:科学出版社,2003.
[9]周云龙,陈飞,孙斌.基于图像小波包信息熵和遗传神经网络的气-液两相流流型识别[J].核动力工程,2008,29(1):115-119.Zhou Yunlong,Chen Fei,Sun Bin.Identification method of gas-liquid two-phase flowregime based on image wavelet packet information entropy and genetic neural network[J].Nuclear Power Engineering,2008,29(1):115-119.
[10]Marceau R J,Soumare S.A unified approach for estimating transient and long-term stability transfer limits[J].IEEE Transaction on Power Systems,1999,14(2):693-701.
[11]穆钢,王宇庭,安军,等.根据受扰轨迹识别电力系统主要振荡模式的信号能量法[J].中国电机工程学报,2007,27(19):7-11.Mu Gang,Wang Yuting,An Jun,et al.Signal energy method for identification of main oscillation mode in power system based on disturbed trajectory[J].Proceedings of the CSEE,2007,27(19):7-11.
[12]汪洋,卢继平,李文沅,等.基于局部网络电压相量的等效模型及其电压稳定性指标[J].中国电机工程学报,2008,28(34):52-59.Wang Yang,Lu Jiping,Li Wenyuan,et al.An Equivalent model and voltage stability index based on local network voltage phasors[J].Proceedings of the CSEE,2008,28(34):52-59.
[13]金敏杰,陈家荣,梅生伟,等.基于改进信号能量法估计暂态稳定极限[J].中国电机工程学报,2004,24(19):1-6.Jin Minjie,Chen Jiarong,Mei Shengwei,et al.Transient stability limit assessment by modified signal energy approach[J].Proceedings of the CSEE,2004,24(19):1-6.
[14]李红智,罗毓珊,王海军,等.圆弧型与X 型开缝翅片空气侧流动与传热特可视化试验[J].化工学报,2008,59(8):1936-1941.Li Hongzhi,Luo Yushan,Wang Haijun,et al.Visualization experiments on air side heat transfer and fluid flow characteristics of arc-type and X-type slotted fin surfaces[J].Journal of Chemical Industry and Engineering,2008,59(8):1936-1941.
[15]张学清,梁军,刘道伟,等.基于信号能量综合指数的电网电压稳定性能分析[J].电力系统保护与控制,2012,40(12):88-94.Zhang Xueqing,Liang Jun,Liu Daowei,et al.Study of power grid voltage stability based on signal energy aggregate index[J].Power System Protection and Control,2012,40(12):88-94.
[16]汤涌,孙华东,易俊,等.基于全微分的戴维南等效参数跟踪算法[J].中国电机工程学报,2009,29(13):48-53.Tang Yong,Sun Huadong,Yi Jun,et al.Tracing algorithm for thevenin equivalent parameters based on complete differential equation[J].Proceedings of the CSEE,2009,29(13):48-53.
[17]周双喜,朱凌志,郭锡玖,等.电力系统电压稳定性及其控制[M].北京:中国电力出版社,2003.
[19]Corsi S,Taranto G N.A real-time voltage instability identification algorithm based on local phasor measurements[J].IEEE Transactions on Power Systems,2008,23(3):1271-1279.
