六相电压源逆变器PWM算法

杨金波 杨贵杰 李铁才

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

1 引言

将传统三相SVPWM 算法扩展到六相逆变器所得到的基于邻近最大两矢量的六相SVPWM 算法只保证了α-β 子空间的电压为正弦而没有考虑z1-z2子空间电压的影响，所以其输出包含了较多的谐波电压，但是却可以得到更大的基波电压调制系数。为此，YiFan Zhao 提出了基于邻近最大四矢量的矢量空间解耦SVPWM 算法，保证了z1-z2子空间的电压为零[1]。Marouani 对该算法进行了更为详尽地分析，给出了具体的实现方案[2,3]。为了更加利于硬件实现，文献[4]提出了一种基于24 扇区的矢量空间解耦SVPWM 算法。将六相逆变器电压矢量分解到两个三相逆变器当中，再利用传统的三相PWM算法分别进行合成，也可以消除低次谐波电压[5-8]。Bojoi 将三相电机零序注入PWM 算法应用到六相系统中，提出了双零序注入PWM 算法，这种算法可以有效地减少运算量[9]。以上研究多集中于正弦调制区，当需要更高的基波电压时，往往直接切换到基于邻近最大两矢量的SVPWM 算法[5]，或将三相过调制SVPWM 算法引入到六相逆变器中[7]，前者注入的谐波含量过大，后者产生的11、13 次谐波会引起转矩脉动。本文讨论了一种基于邻近最大四矢量的六相电压源逆变器SVPWM 算法。该算法在正弦调制区内输出正弦相电压，在非正弦调制区内通过注入尽量小的谐波电压以提高母线电压利用率，实现了输出电压从正弦调制区到非正弦调制区的平滑过渡。通过对PWM 波形中心化处理，使得算法更加易于实现。实验结果验证了算法的有效性。

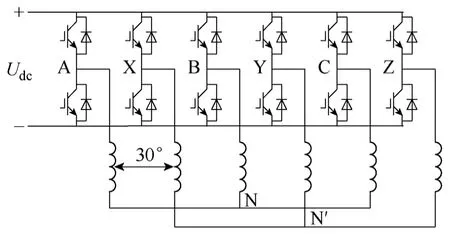
图1 六相逆变器供电的双三相电机Fig.1 Six-phase inverter fed dual three-phase motor

2 六相逆变器的电压矢量

六相逆变器共有64 个开关状态，每一个开关状态在α-β 平面和z1-z2平面所对应的电压矢量可以分别由式（1）和式（2）决定

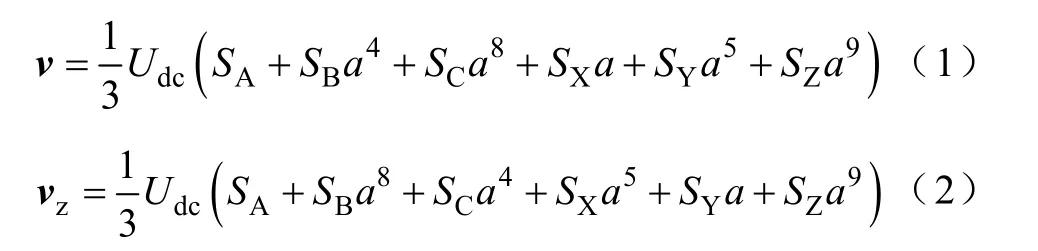
式中，a=ej30°；S表示每一个桥臂的开关状态，S=1时表示上桥臂导通，S=0 时表示下桥臂导通。这样就可以得到α-β 与z1-z2平面的电压矢量图，如图2所示。图中的每一个电压矢量用一个八进制数表示，与八进制数相对应的二进制数代表了逆变器的开关状态，从高位到低位依次为（ABCXYZ）。每一个平面包括60 个有效矢量和4 个处于原点位置的零矢量（00,07,70,77）。根据电压矢量幅值的大小，每一个平面内的电压矢量都可以被分成四组，每一组都可以构成一个正十二边形。在α-β平面具有最大幅值的矢量在z1-z2平面的幅值反而最小，反之亦然。定义调制系数为相电压基波幅值与母线电压的比值

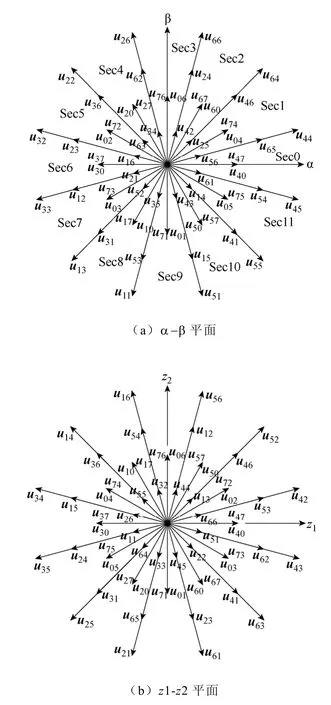
图2 六相逆变器电压矢量图Fig.2 Diagram of six phase inverter voltage vectors

3 基于邻近两矢量的SVPWM 算法

由于电压中的基波分量都被映射到α-β 平面当中，所以基波电压矢量的合成要在α-β 平面中完成。为了提高电压利用率，减少开关损耗，选取α-β 平面中幅值最大的12 个矢量作为基本矢量，可以将整个平面分成12 个扇区，如图2a 所示。

任一扇区内的电压矢量都可以由相邻的两个基本矢量和一个零矢量进行合成。例如当参考矢量ur落在第0 扇区内时，可以由u45和u44来合成。根据伏秒平衡原则可以得到各矢量的作用时间，如图3所示。

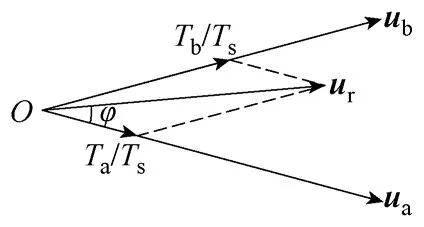
图3 基于最大两矢量的SVPWM 算法Fig.3 SVPWM algorithm based on two largest vectors

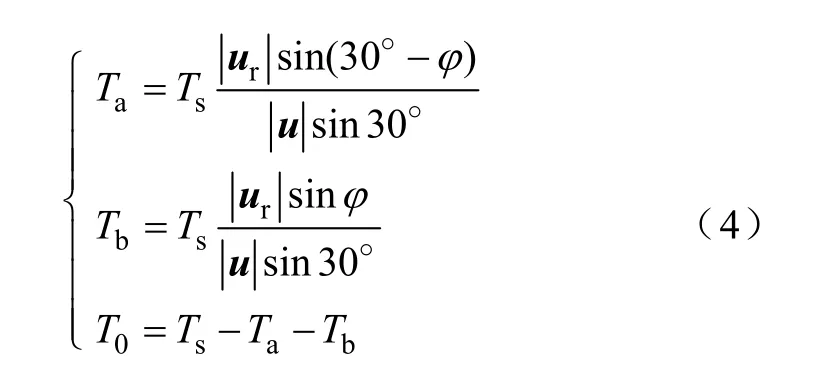
该方法的调制范围可以到达正十二边形的内切圆，也就是说所能合成的电压矢量的最大幅值为，即0.622Udc。这种方法只是三相SVPWM 算法的简单推广，并没有考虑六相系统含有多个谐波子空间的特点。由于z1-z2子空间的电压并没有进行控制，所以其输出相电压并不是正弦波，而包含了较多的5 次、7 次谐波。

严寒地区高速铁路底座板粉化原因及整治对策研究……………………………………………………… 许鹤（10-142）

4 基于邻近四矢量的SVPWM 算法

4.1 正弦调制算法

Zhao 提出了基于邻近最大四矢量的矢量空间解耦SVPWM 算法，如在第0 扇区，则选用55、45、44、64 四个电压矢量。这种方法同时控制了两个子空间的电压分量，既保证了在α-β 平面合成所需要的基波电压，又保证了z1-z2子空间的合成电压为零。其计算过程就是求解一个五元一次线性方程组。

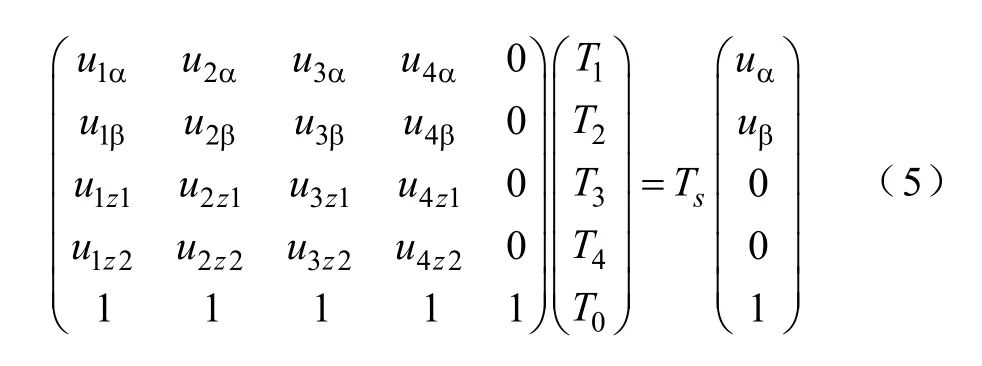
这种方法消除了低次谐波，调制电压的幅值可以达到0.577Udc。由此可见，当调制系数大于0.577时，便进入了非正弦调制区，必须通过注入低次谐波的方法来提高电压利用率。虽然两矢量合成方法的调制系数可以达到0.622，但是所注入的谐波含量过大。文献[10]提出的基于预合成矢量的算法和Zhao的方法本质上是一样的，但是更易于将四矢量SVPWM 算法推广到非正弦调制区，通过注入更少的谐波来得到与两矢量SVPWM 算法相同的调制系数。

如图4 所示，用u1～u3合成一个新的矢量ua，当u1和u3的作用时间相同时所得到的新矢量和u2方向相同，设u2的作用时间为aTs，则u1和u3的作用时间都为0.5×(1-a)Ts。这样可以得到矢量ua在α-β与z1-z2平面的幅值分别为

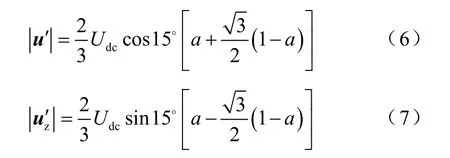
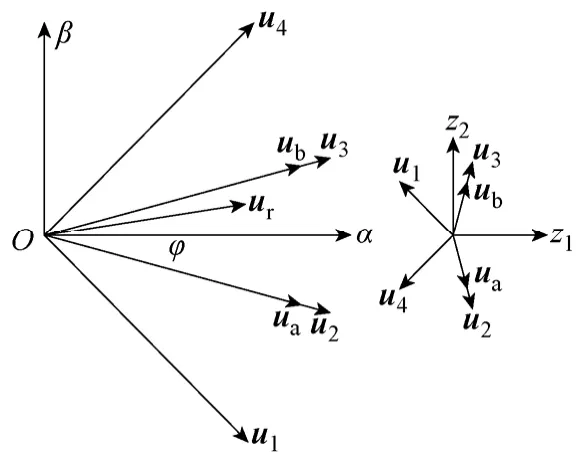
图4 基于最大四矢量的SVPWM 算法Fig.4 SVPWM algorithm based on four largest vectors

同理，u2～u4合成一个新的矢量ub。这样一共可以重新合成12 个电压矢量，这些矢量在两个平面的分布与之前完全相同，只是幅值大小不一样。在正弦调制范围内时只需令，可以得到。将式（4）中的用代替，就可以得出合成给定参考电压ur所需要的预合成矢量的作用时间Ta和Tb为

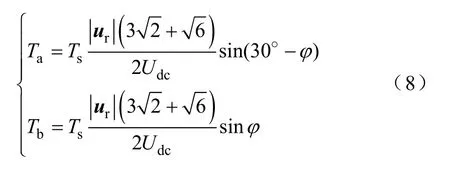
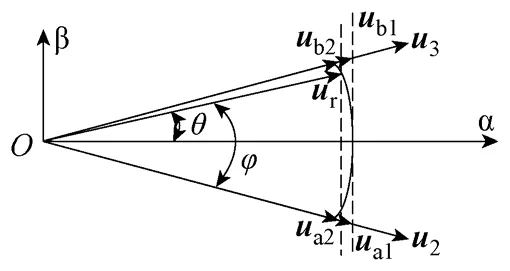
图5 非正弦SVPWM 算法Fig.5 Non-sinusoidal SVPWM algorithm

然后再将Ta和Tb分配到真实存在的矢量u1～u4中。

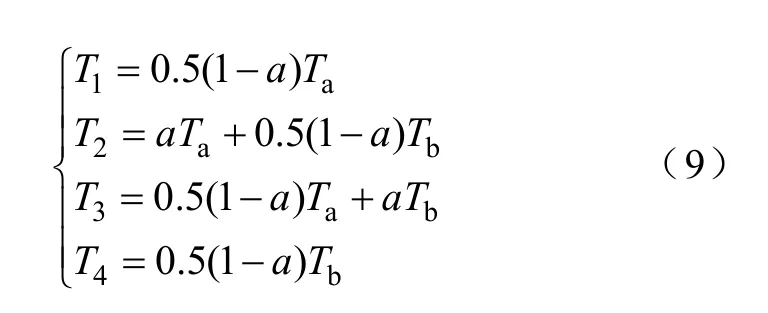
这时按照式（8）和式（9）计算的结果和式（5）完全相同，最大调制电压为 0.577Udc。

4.2 非正弦调制算法1

在非正弦调制范围内，可以通过选择适当的a值来提高基波电压幅值。从式（6）和式（7）中可以看出，a的值越大，越大，所能合成的基波电压矢量就越大，但是相应的谐波电压矢量幅值也会越大。当a增加到1 时，则完全变成两矢量SVPWM的情况。由此可见，在能够满足合成电压矢量的情况下，越小，所注入的谐波就越小。考虑到当一定时，其所能合成的基波电压矢量幅值为cos15°。令

便可以得到a的表达式

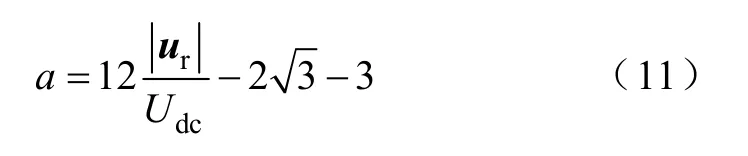
代入式（4），可以得到

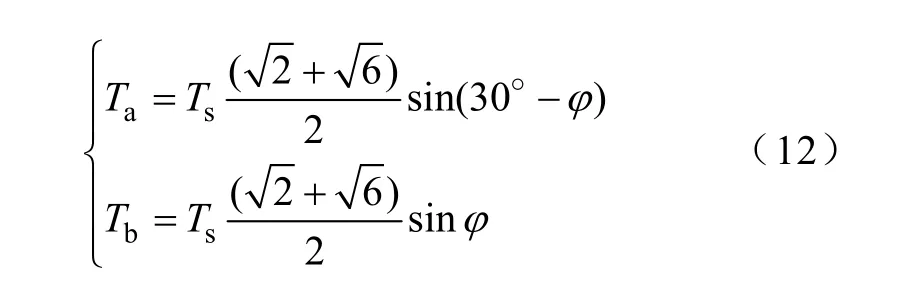
这两个预合成矢量如图5 中的ua1和ub1所示，它们的作用时间已经和参考电压矢量的幅值无关，而只与其相位有关。随着给定电压幅值从0.577Udc增加到0.622Udc，a的值也从逐渐变成1，算法也从最大四矢量合成的情况逐渐过渡到最大两矢量合成的情况，从而实现了从正弦调制区到非正弦调制区的平滑过渡。

4.3 非正弦调制算法2

以上的分析是基于所能合成的最大电压矢量幅值，根据正十二边形内切圆的半径大小来选择预合成矢量的大小，这种方法并没有考虑到参考电压矢量角度的变化。当一定时，由12 个预合成矢量构成的正十二边形内部的所有参考电压矢量都可以进行合成，因此当时，可以假定参考电压矢量正好落在正十二边形的边界上，这样所需的预合成电压矢量的幅值在θ≠ 0时与算法 1相比可以进一步减小，如图5 中的ua2和ub2所示，θ为ur与扇区角平分线的夹角为（θ=φ-15°）。这时的预合成矢量的大小为

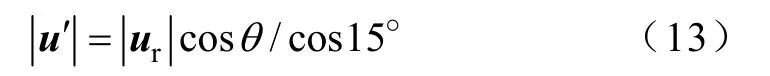
分别代入式（5）和式（7），可以得到

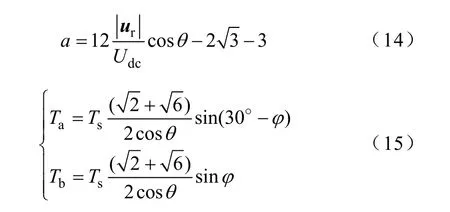
从上式中可以看出，预合成矢量的作用时间也仅与参考电压矢量的相位有关，与幅值无关，而且由于落在正十二边形的边界上，这两个矢量作用时间之和应该正好等于1 个PWM 周期。图6 给出了在不同调制系数和调制算法下的A 相桥臂电压，相电压平均值波形图和相电压的谐波分布图。所谓的平均电压指的是一个PWM 周期内电压的平均值，这里主要考察的是算法本身所产生的谐波大小，所以忽略了PWM 开关过程所产生的高次谐波的影响。

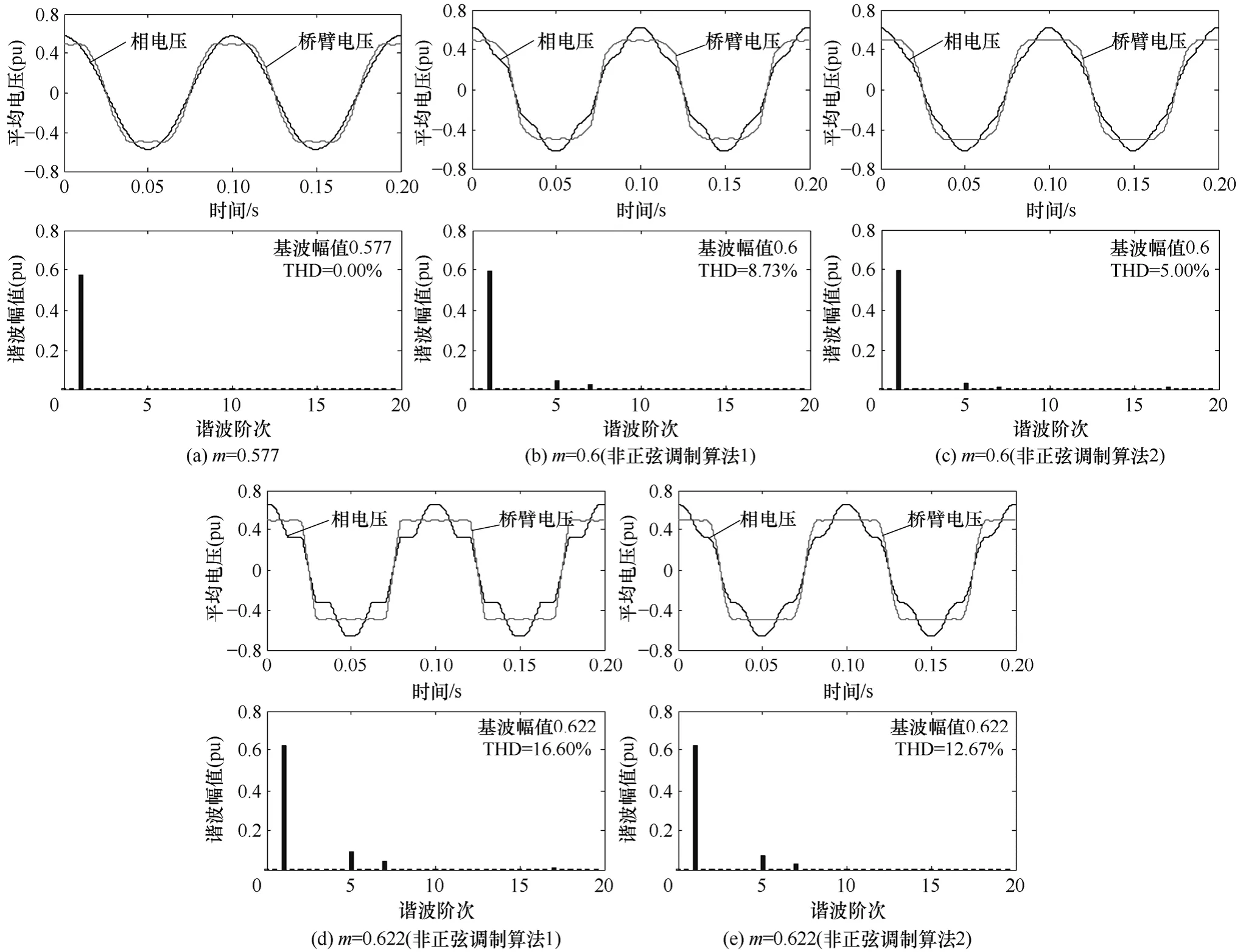
图6 不同调制系数下的桥臂电压、相电压平均值波形和相电压谐波分析Fig.6 Average leg voltage,phase voltage and its harmonic spectra in different modulation indexes

桥臂电压指的是逆变器输出端相对于母线电压中点的电位，图6 中的电压值均以母线电压为基值采用标幺值表示。从图6 中可以看出，所有的桥臂电压都在[－0.5，0.5]的范围内，满足逆变器输出桥臂电压的要求。图6a 由于调制系数处于正弦调制区内，输出的相电压不含低次谐 波。随着调制系数的增加，谐波含量也逐渐增加，非正弦调制算法2的谐波畸变率比算法1 要略小一些。图6d 所示的是算法1 在最大调制系数下的波形，是完全采用邻近两个最大矢量合成的，其畸变率和谐波分布适用于所有最大两矢量合成的情况，只是幅值会有所不同。由此可见，上文中的调制算法2 能够在注入更少谐波的情况下提高基波的调制范围。

4.4 PWM 波形的中心化处理

在基于邻近最大四矢量SVPWM 算法中，如果按照一个PWM 周期内每一个功率器件开关一次来分配占空比的话，可以发现PWM 波形并不是中心对称的。图 7 给出了参考矢量为 0.4Udc5°∠ 时的PWM 波形。不对称的波形会增加输出电压的高次谐波，而且不利于硬件实现，文献[2]用两个周期实现了PWM 波形的对称输出，这样会导致每两个PWM 周期才能更新一次输出电压，如图7a 所示。考虑到每一个桥臂的输出电压的平均值只与占空比大小有关，而与脉冲的位置无关，可以对PWM 波形进行中心化处理，把每一路脉冲都移到中心位置，如图7b 所示。由于桥臂电压的平均值不变，相电压的平均值也不会发生变化，基波和低次谐波含量与原先相同，只是由开关信号所产生的高次谐波含量会不一样。

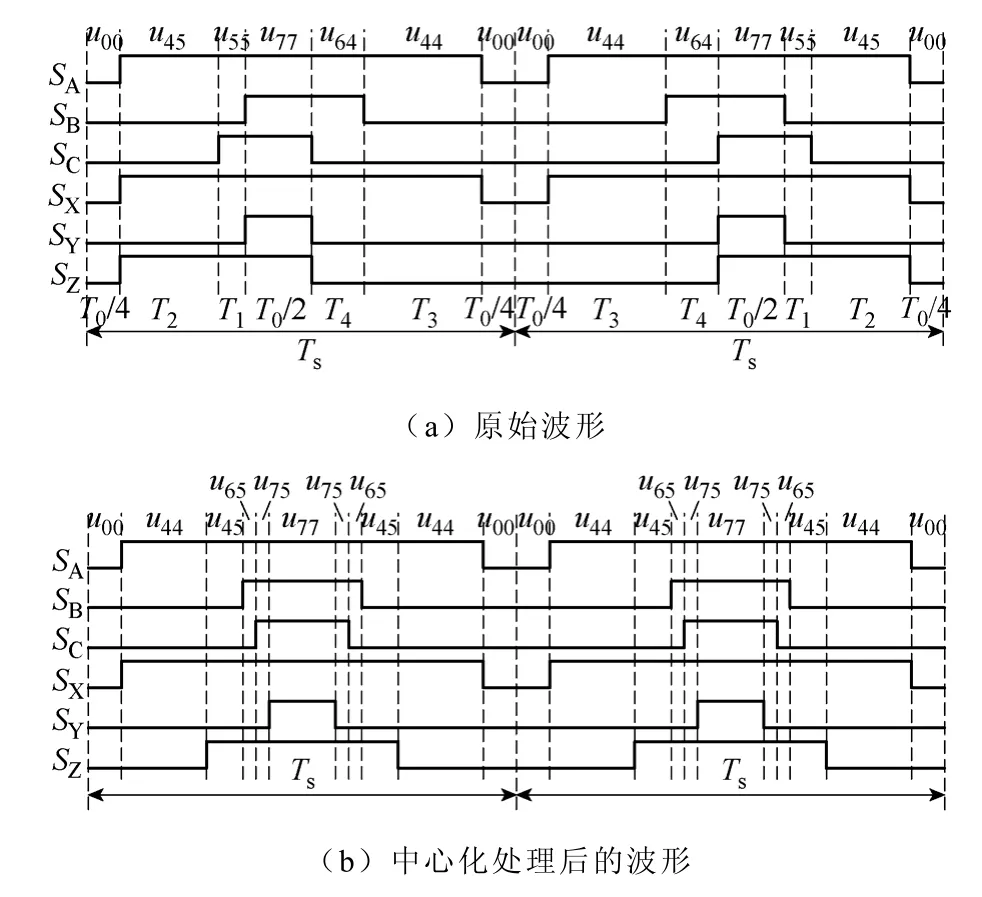
图7 第0 扇区上桥臂PWM 波形图Fig.7 PWM waveform of upper leg in sector 0

图7b 中作用的电压矢量已经发生了变化，u55和u64两个矢量被新矢量u65和u75所代替。当参考电压矢量变化时，中心化处理后所产生的新矢量也不一样，例如当参考矢量变成0.4Udc∠－5°时，新的作用矢量将是u44、u45、u55、u75。所以如果直接选用能够中心对称的矢量来合成参考矢量的话就需要划分更多的扇区且针对每个扇区所选择的电压矢量的分布也不一致，这会进一步增加算法的复杂性。

5 实验结果

对文中分析的基于四矢量的正弦调制算法和非正弦调制算法2 进行了实验验证。实验中用到的控制器为Infineon 公司的XE164，该芯片支持18 路PWM 输出，完全满足六相逆变器的需要。实验中对PWM 波形进行了中心化处理，便于硬件实现。给定的电压频率为10Hz，开关频率为10kHz。不同调制系数下的实验结果如图8 所示。

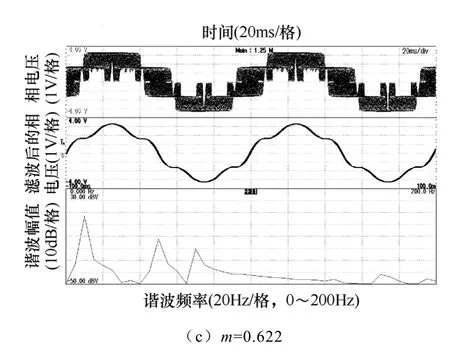
图8 最大四矢量SVPWM 算法实验结果Fig.8 Experimental results of SVPWM algorithm based on four largest voltage vectors

每一个图中从上到下依次为相电压波形，相电压滤波后的波形（截止频率800Hz）和相电压（滤波前）的频谱分析。滤波后的波形和图6 分析的结果基本一致。随着调制系数的增加，谐波含量也在逐渐增加。由于示波器频谱分析的纵坐标采用的是分贝，因此基波和谐波之间的差距比直接用幅值表示时要小一些。

6 结论

通过对最大四矢量SVPWM 算法的分析并结合预合成矢量的计算方法，本文提出了两种非正弦调制策略，通过适当注入6k±1（k=1,3,5,…）次谐波来提高基波电压的调制系数，从而将四矢量SVPWM 算法的调制范围扩展到α-β 子空间所能达到的最大值，并实现了从正弦调制区到非正弦调制区的平滑过渡。其中算法2 由于考虑到了参考电压矢量角度的变化，可以获得更低的谐波含量。实验结果与理论分析相符合，从而验证了算法的有效性。

[1]Zhao Yifan,Lipo T A.Space vector PWM control of dual three-phase induction machine using vector space decomposition[J].IEEE Transactions on Industry Applications,1995,31(5):1100-1109.

[2]Hadiouche D,Baghli L,Rezzoug A.Space-vector PWM techniques for dual three-phase AC machine:analysis,performance evaluation,and DSP implementation[J].IEEE Transactions on Industry Applications,2006,42(4):1112-1122.

[3]Marouani K,Baghli L,Hadiouche D,et al.Discontinuous SVPWM techniques for double star induction motor drive control[C].32nd Annual Conference on Industrial Electronics,2006:902-907.

[4]Marouani K,Baghli L,Hadiouche D,et al.A new PWM strategy based on a 24-sector vector space decomposition for a six-phase VSI-fed dual stator induction motor[J].IEEE Transactions on Industrial Electronics,2008,55(5):1910-1920.

[5]Gopakumar K,Ranganathan V T,Bhat S R.An efficient PWM technique for split phase induction motor operation using dual voltage source inverters[C].IEEE Institute for Advanced Studies Annual Meeting,1993:582-587.

[6]Yazdani D,Khajehoddin S A,Bakhshai A,et al.A generalized space vector classification technique for six-phase inverters[C].Power Electronics Specialists Conference,2007:2050-2054.

[7]Yazdani D,Khajehoddin S A,Bakhshai A,et al.Full utilization of theinverter in split-phase drives by means of a dual three-phase space vector classification algorithm[J].IEEE Transactions on Industry Electronics,2009,56(1):120-129.

[8]Grandi G,Serra G,Tani A.Space vector modulation of a six-phase VSI based on three-phase decomposi-tion[C].International Symposium on Power Electronics,Electrical Drives,Automation and Motion,2008:674-679.

[9]Bojoi R,Lazzari M,Profumo F,et al.Digital field-oriented control for dual three-phase induction motor drives[J].IEEE Transactions on Industry Applications,2003(3):752-760.

[10]Li Shan,Xiao Huihui,Chen Hongyan.The research of SVPWM control technique of double three-phase induction machine[C].International Conference on Electrical Machines and Systems,2005:109-114.