笼型异步电动机径向电磁力波的有限元计算

王 荀 邱阿瑞

（1.北京机械设备研究所 北京 100854 2.清华大学电机工程与应用电子技术系 电力系统及大型发电设备控制和仿真国家重点实验室 北京 100084）

1 引言

异步电动机广泛地应用于工农业生产及国防等各个领域，随着近年来对噪声污染的重视，低噪声电机的需求越来越多。电磁噪声是由径向电磁力激励定子振动而产生，是异步电动机的一个主要噪声源[1-3]。径向电磁力含有许多谐波，称为径向电磁力波，当电磁力波和电机机械模态的阶次一致且频率相接近时，会导致定子共振从而引起大的电磁噪声。为了对电磁噪声进行分析预估以及降低电磁噪声，有必要分析和计算径向电磁力及其谐波。

已有一些文献对电磁力作了研究：文献[2-5]对异步电机电磁力波产生的原因在理论上进行了定性分析，并利用解析法定量计算；由于气隙磁场变化复杂，解析法计算电磁力波时准确度稍差。近年来有限元法应用于计算电磁力，文献[6-8]利用有限元法分别对爪极电机、开关磁阻电机和永磁电机的电磁力进行研究；文献[9，10]基于二维瞬态有限元计算异步电机的电磁力，文中作为电磁计算的输入是电流（实际电机输入为定子机端电压），该电流是由电路模型计算得到，与实际电机的电流存在差异；这些文献对电磁力波没有作详细的分析，而电磁力波的阶次、频率和幅值是电磁噪声分析时的重要问题。

本文基于场路耦合时步有限元法计算笼型异步电动机的气隙磁通密度和径向电磁力，并基于二维离散傅里叶分析求解它们的谐波含量。探讨齿槽和转差率对磁通密度和径向电磁力的影响，以及磁通密度波和电磁力波之间的关系。分析径向电磁力波与实测电磁噪声的对应关系。

2 场路耦合时步有限元的仿真计算

以一台小型直槽笼型异步电动机为例，基本参数为：额定电压为380V，额定频率为50Hz，定子绕组相数为3，极对数为2，定子槽数为36，转子槽数为28，定子绕组为双层绕组，定子绕组联结为三角形接法，定子绕组并联支路数为1，铁心长度为 120mm，气隙长度为 0.365mm，定子外径为175mm，定子内径为110.05mm，转子内径为38mm。

2.1 数学模型

场路耦合时步有限元法是将磁场方程和电路方程进行耦合，并计及转子运动，可充分考虑开槽、铁心饱和、涡流、绕组形式和联接方式、转子运动、供电电源等对磁场带来的影响。

异步电动机正常运行时，铁心横截面上磁场存在周期性，实例电机极对数为2，磁场在整圆周上存在2 个整周期。利用圆周方向上磁场的周期性，采用二维剖分，为了缩短计算时间只剖分半个周期的场域，求解区域的有限元网格如图1 所示。在设电机电磁场为似稳场等基本假设条件下[11]，基于Maxwell 方程可得二维瞬态电磁场方程为

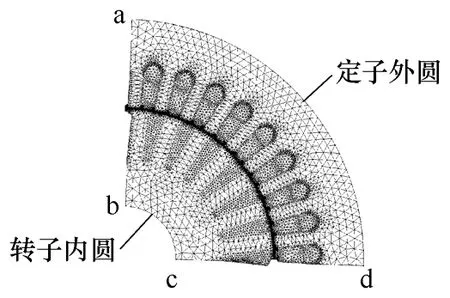
图1 有限元网格Fig.1 Finite element mesh

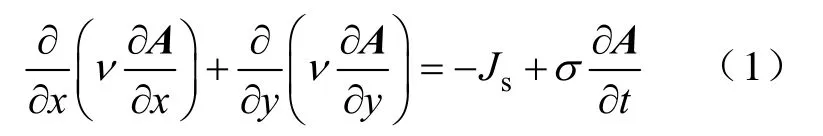
式中A—轴向矢量磁位；

Js—源电流密度，存在于槽中导体区域；

v—磁阻率；

σ—电导率。

边界条件：①在定子外圆和转子内圆上A=0；②径向两个外边界上矢量磁位相反，。

根据定子绕组和外电路的联结方式，选取如图2 所示的回路（回路法可考虑各相绕组之间的环流），则定子侧的回路电压方程为

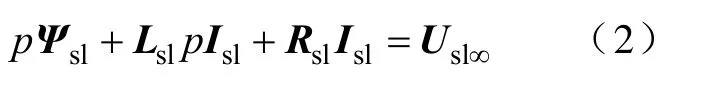
式中Ψs1—定子回路主磁链矢量；

Is1—定子回路电流矢量；

Ls1—定子回路漏感矩阵；

Rs1—定子回路电阻矩阵；

Usl∞—定子回路电源矢量；

p—算子，p=d/(dt)。

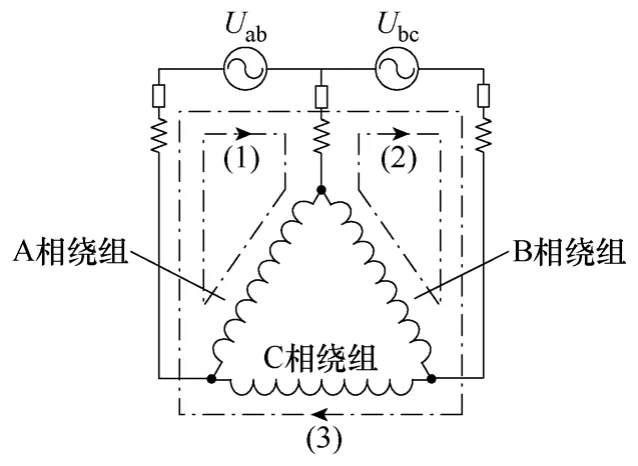
图2 定子回路示意图Fig.2 Sketch map of stator loops

转子回路的选取是根据剖分区域中导条和端环连接而形成的实际网孔，转子回路电压方程为

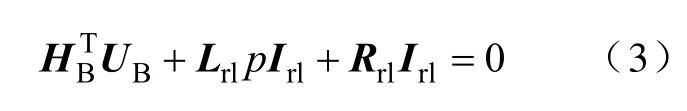
式中UB—铁心区域内转子导条的电压矢量；

Ir1—转子回路电流矢量；

Lr1—转子回路在铁心外的漏感矩阵；

Rr1—转子回路在铁心外的电阻矩阵；

HB—导条与转子回路之间的关联矩阵。

以第n号转子导条为例，列写转子导条的电流方程，即

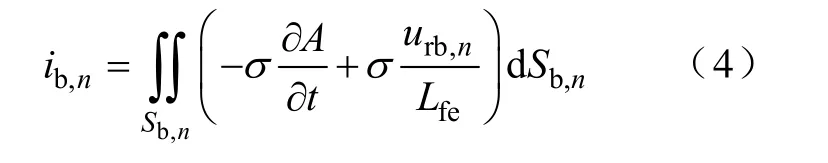
式中ib,n—第n号转子导条的电流；

urb,n—铁心区域内第n号转子导条的电压；

Lfe—铁心长度；

Sb,n—第n号转子导条区域。

用伽辽金法对式（1）在剖分场域中进行离散可得

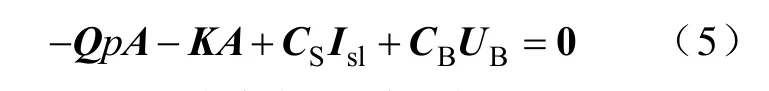
式中A—节点矢量磁位矢量；

Q，K，CS和CB—系数矩阵（限于篇幅这里不给 出具体形式），且有

CS的求解方法：根据定子回路电流可求出线圈电流，再由线圈所占的单元面积求出电流密度，进而可得CS；求解时场域矢量磁位A(x，y)=NTA，N为单元形状函数的矢量；S表示剖分场域。

将式（2）中定子回路主磁链对时间微分（pΨs1）用节点矢量磁位表达以实现场路耦合；将式（4）中转子导条区域的涡流电流密度亦用节点矢量磁位表达，则由式（2）～式（5）可得笼型异步电动机的场路耦合方程为

式中，X为解矢量，且有

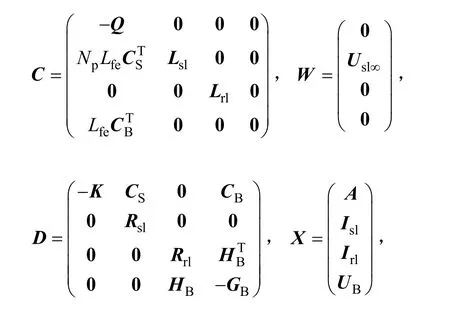
其中Np—整圆周对剖分区域的倍数；

GB—铁心范围内转子导条的电导矩阵。

转子的旋转运动方程为

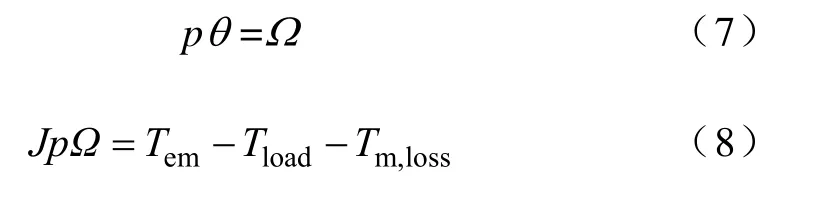
式中θ—转子机械位置角；

Ω—转子机械角速度；

J—转动惯量；

Tem—电磁转矩；

Tload—负载转矩；

Tm,loss—机械损耗引起的转矩。

采用Crank-Nicolson 方法对式（6）在时间域中离散，从而可得非线性代数方程组，并考虑到转子的运动方程，时间步进地求解这个非线性代数方程组，可得每一时刻的节点矢量磁位、回路电流、转子机械位置角和转子机械角速度，具体的求解方法可参阅相关文献。

2.2 仿真结果的试验验证

基于以上场路耦合时步有限元数学模型，利用VC++编写了仿真软件。

定子机端引线接到380V、50Hz的正弦电压源上，仿真计算的空载稳态定子相电流波形如图 3a所示；利用数字示波器试验测量的空载稳态定子相电流波形如图3b 所示。定子绕组相电流谐波含量的计算值和实测值的比较见表1，表中误差为（计算值－实测值）/实测值。

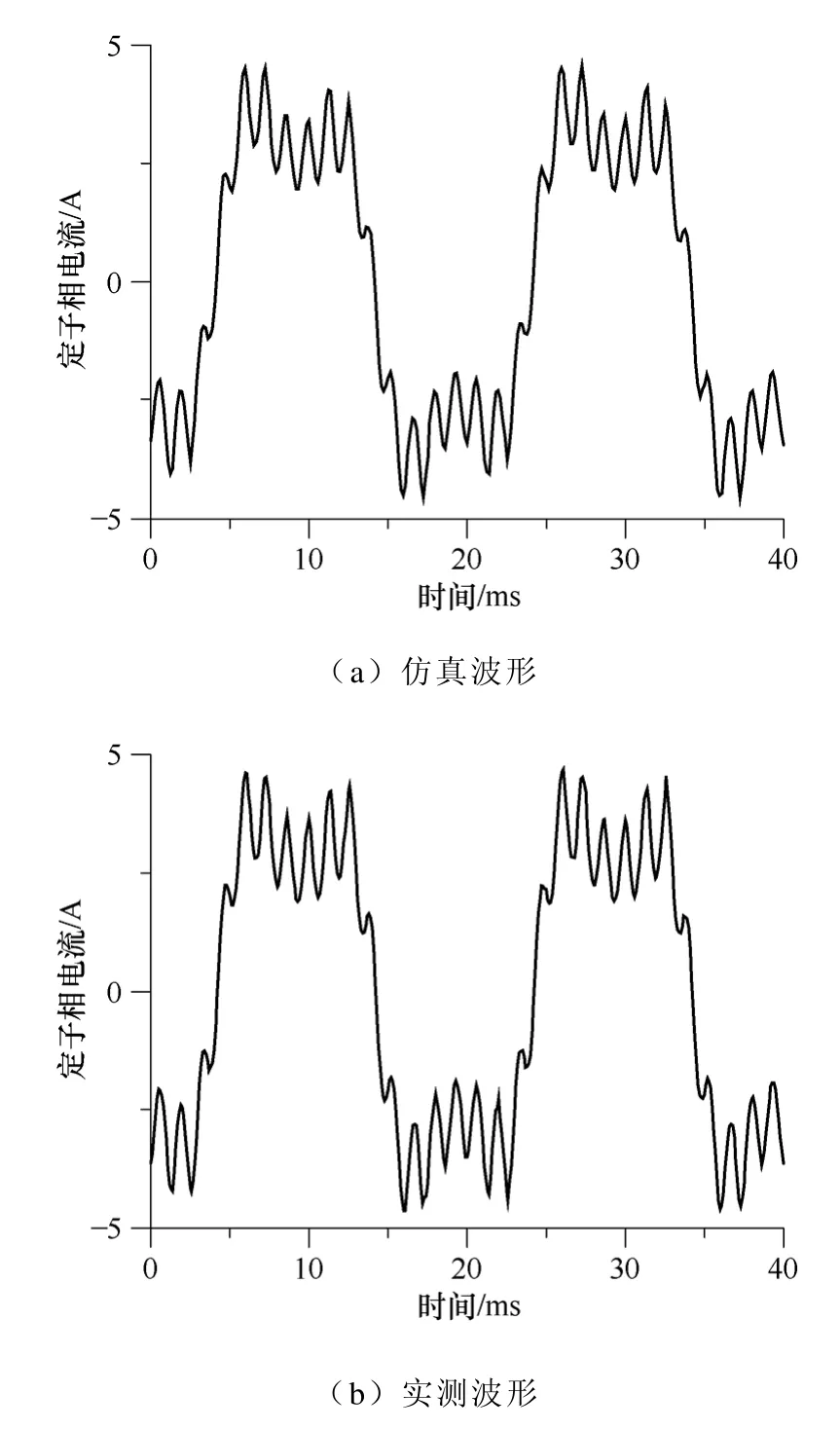
图3 定子相电流Fig.3 Stator phase current

表1 定子相电流谐波计算值和实测值的比较Tab.1 Comparison between stator phase current harmonics of the calculation and those of the experiment

3 气隙磁通密度的分析与计算

作用于齿表面上的电磁力由气隙磁场产生，若要分析引起电磁振动和噪声的电磁力及其谐波，首先需要分析气隙磁通密度的变化规律和谐波含量。

3.1 解析分析

利用有限元法定量计算气隙磁通密度之前，先利用解析法定性讨论一下异步电机中径向磁通密度的主要谐波含量，以便将有限元计算结果与解析分析结果进行比较。

利用磁路法分析时异步电机径向磁通密度波为

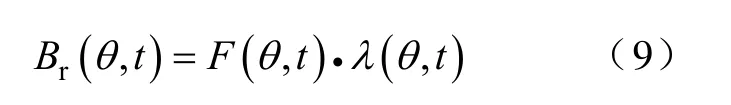
式中F(θ,t)—磁动势；

λ(θ,t)—气隙磁导系数。

F(θ,t)中包含定转子电流产生的基波磁动势和谐波磁动势。λ(θ,t)中包含定转子开槽引起的气隙磁导系数和铁心饱和引起的气隙磁导系数。F(θ,t)和λ(θ,t)的具体表达形式可参阅文献[3]。由式（9）得到的主要径向磁通密度波见表2[3]，表中：pn为电机（基波）的极对数；Z1为定子槽数；Z2为转子槽数；m1为定子绕组的相数；fr=(1-s)f1/pn，s为转差率，f1为定子基波电流的频率；kst、krt、ksa和c的取值均为±1，±2，±3，…；当极对数和频率为同号时表示正转波，异号时表示反转波。表2 中序号2 表示的磁通密度波为定子齿谐波，极对数m=pn+kstZ1，kst为定子齿谐波的阶数，例如kst=±1 时称为一阶定子齿谐波。序号3 表示的磁通密度波为转子齿谐波，极对数m=pn+krtZ2，krt为转子齿谐波的阶数。与转子开槽相关的气隙磁导系数谐波引起的磁通密度波（见表2 中序号3 和序号4 表示的磁通密度波）的频率均与转差率有关，转速变化时这些磁通密度波的频率均变化。序号5 为铁心饱和引起的磁通密度波，序号6 表示的磁通密度波为定子绕组相带谐波。

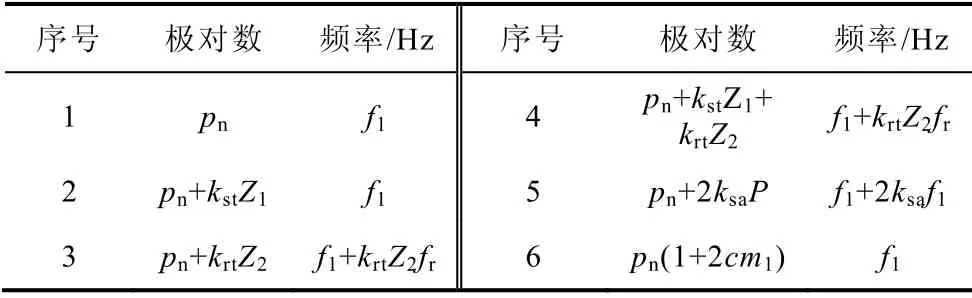
表2 主要的径向磁通密度波Tab.2 Main radial flux density wave

3.2 有限元计算

利用场路耦合时步有限元数学模型可计算出每一个时刻的节点矢量磁位，由气隙中节点矢量磁位可求出气隙磁通密度。

空载稳态时(s≈0)，径向和周向磁通密度的空间分布分别如图4a、4b 所示。由图4a 可见，齿上径向磁通密度的变化趋势主要受定子分布绕组电流密度的影响，径向磁通密度在定子齿表面上近似是平的，有个别定子齿表面上径向磁通密度会存在突变，这是由于该位置存在转子槽口，而在定子槽位置处的径向磁通密度大大减小。由图4b 可见，周向磁通密度在定子齿表面上几乎为0，在槽口和齿的边界附近变化比较剧烈，而且沿圆周方向上一个定子齿两个边界处周向磁通密度方向相反。径向和周向磁通密度主要受定转子开槽和转子角位置的影响，在定子齿表面上磁通密度几乎沿径向进入定子齿，在槽口和齿的边界附近存在周向磁通密度。空载稳态和转差率s≈0.05 时，单个定子齿表面周向中心点的径向磁通密度随时间的变化如图5 所示。由图5 可见，径向磁通密度随时间的变化规律随转速的不同而不同，即转速变化气隙磁场亦改变。

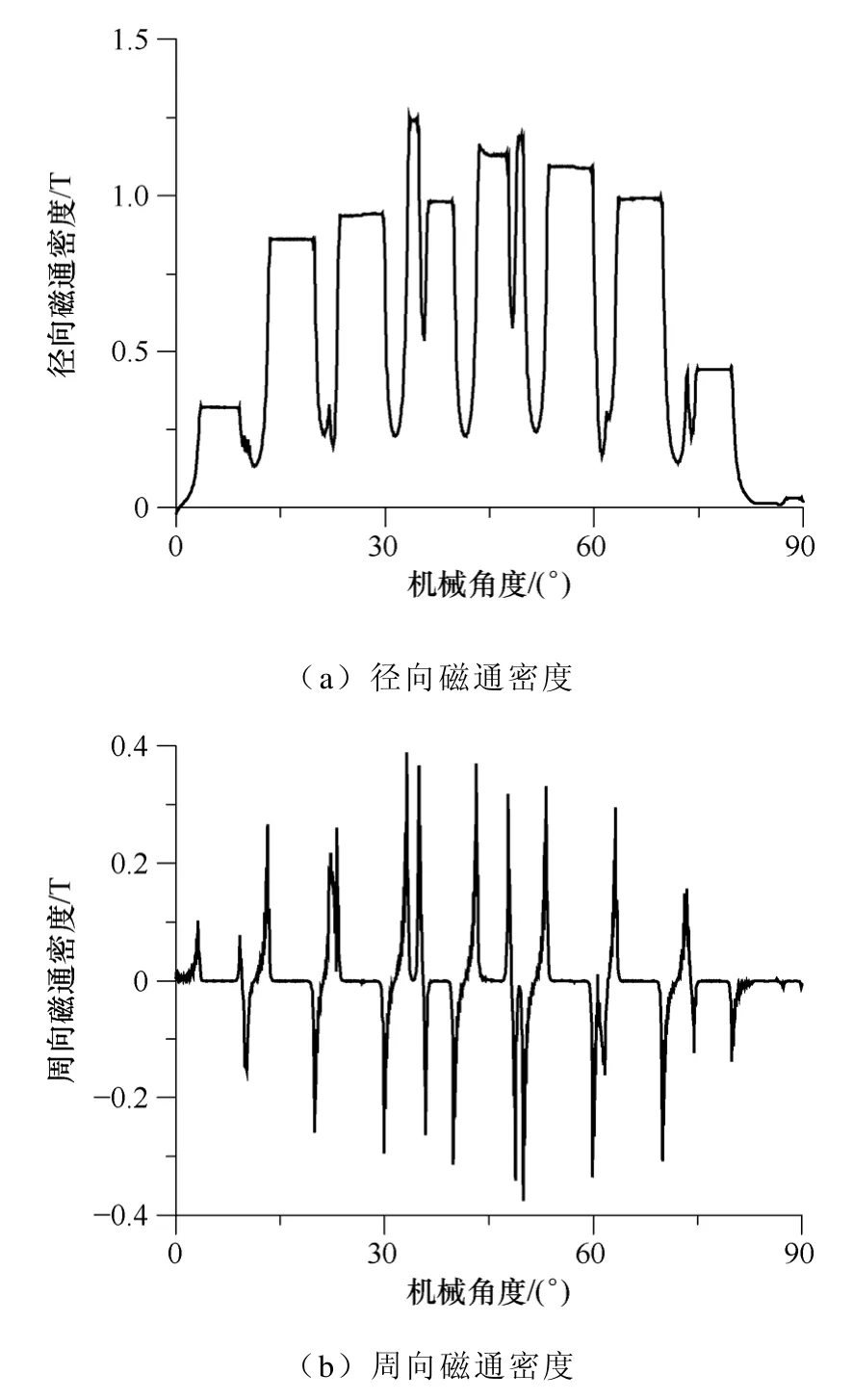
图4 径向和周向磁通密度的空间分布Fig.4 Space distribution of radial and circumferential flux density

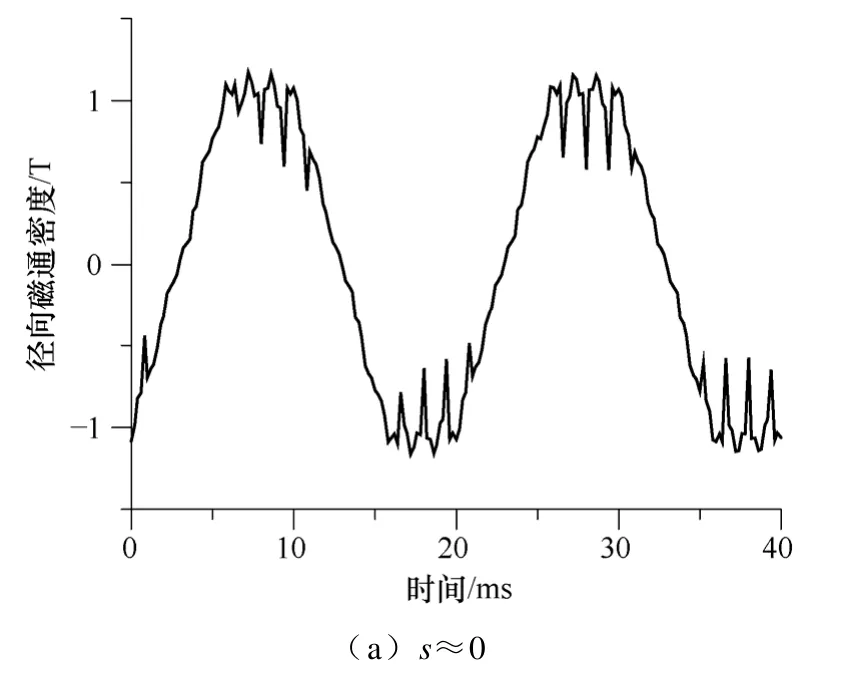
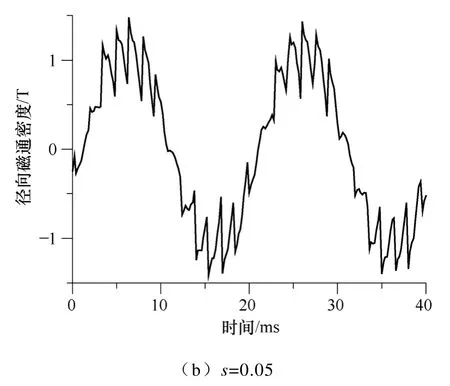
图5 径向磁通密度随时间的变化Fig.5 Variation of radial flux density with time

气隙磁通密度不但在空间圆周方向上变化，而且还随时间变化，它的谐波（即磁通密度波）为行波。旋转磁场谐波理论广泛地应用于电机磁场分析，可将时空变化的气隙径向磁通密度利用无穷多个正转或者反转的径向磁通密度波来线性叠加，即

式中m，n—对应空间谐波和时间谐波的次数，均为整数，m的绝对值表示谐波的极对数，m为正整数时表示正转波，m为负整数时表示反转波；

θ—空间圆周方向上的机械角度；

t—时间；

Br,mn—幅值；

θr,mn—初始角度；

ωB,n—时间角频率，ωB,n=2πfB,n；

fB,n—频率；

下标r 表示径向分量。

将时空变化的磁通密度进行二维离散傅里叶分析（本文利用的是Matlab 中FFT2 命令），即计算磁通密度的空间谱和时间谱，可得到式（10）中每一个磁通密度波的极对数、频率、幅值、相角和转向。式（10）中磁通密度波的频率ωB,n=nω，其中：ω为角频率分辨率，且有ω=2π/T，T为分析磁通密度变化的总时间（s）；n为整数且n≥0，n的最大取值决定所分析的最高频率，它取决于计算磁通密度的步数。T越大则角频率分辨率ω就越小。本文将1s 时间内的磁通密度进行傅里叶分析，频率分辨率为1Hz。

以空载稳态为例，计算的主要径向磁通密度波见表3。按幅值大小排序列出，极对数为正表示正转波，为负表示反转波，表中还给出了径向磁通密度波的极对数和频率对应的解析表达式。负载时磁通密度波的计算方法类似处理，不再赘述。

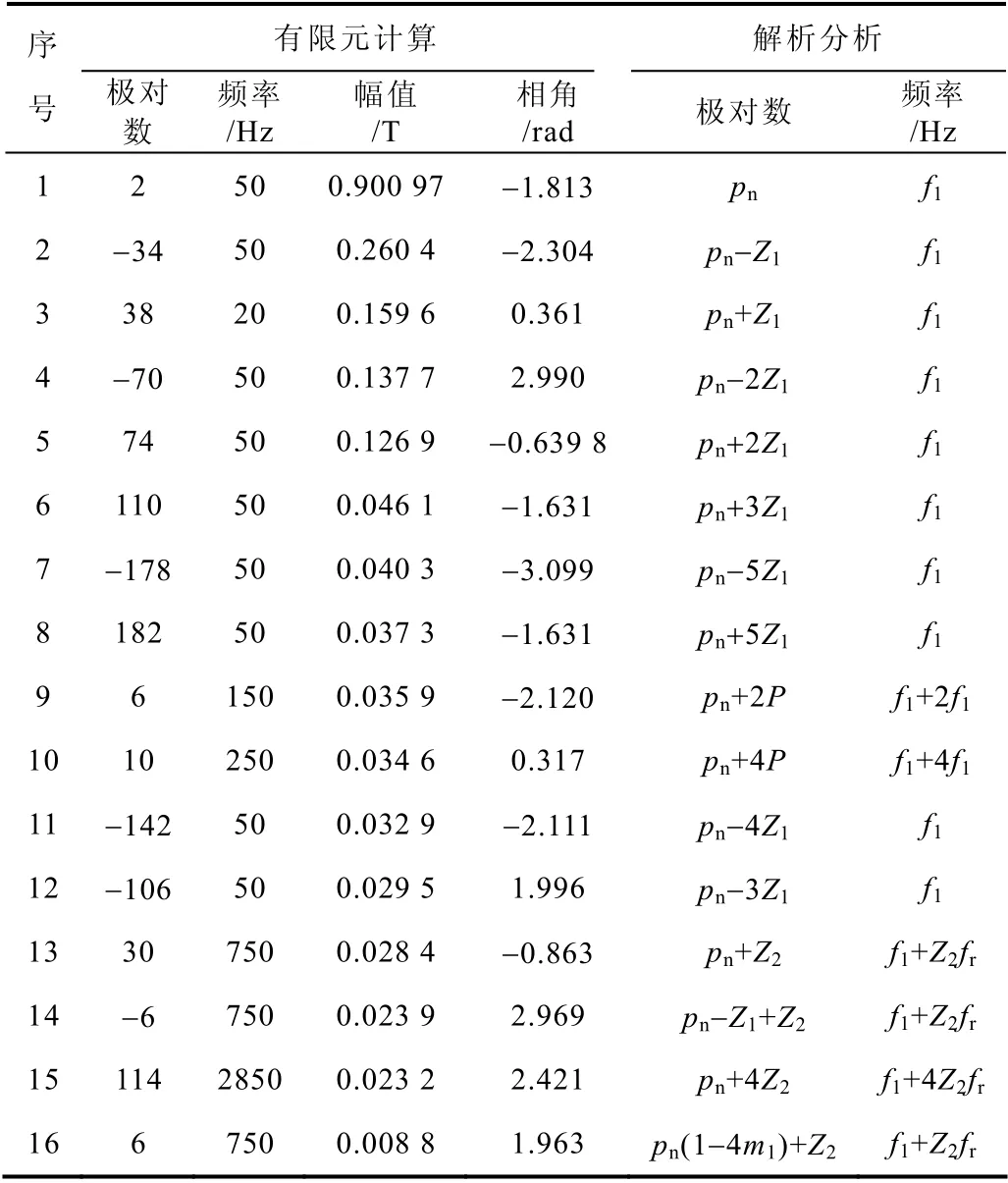
表3 径向磁通密度波Tab.3 Radial flux density waves

磁通密度中会存在同一个极对数但频率不同的谐波。由表3 可看出，6 对极就存三个不同的谐波，一个为150Hz，另外两个为750Hz，而且它们的转向也不同。若对图4a 所示的某时刻径向磁通密度的空间分布，利用常用的一维离散傅里叶分析只能得到磁通密度波的极对数、幅值和相角，从而无法分辨出这三个不同的谐波。

由于磁通密度谐波会在绕组中形成磁链，进而产生感应电动势谐波，从而导致电流谐波，即磁通密度波和电流谐波存在对应关系。电流谐波计算的准确度可间接验证气隙磁通密度波计算的准确度。由图3a 和3b的比较及表1 可知，电流谐波计算是比较准确的，故磁通密度波计算亦是较准确的。

4 径向电磁力的分析与计算

为了分析方便，常将电磁力分为径向分量和周向分量。周向电磁力形成电磁转矩，是电动机转动所需要的。径向电磁力是不可避免的，它会引起定子振动而产生电磁噪声，以下重点探讨径向电磁力。

4.1 解析分析

异步电机的周向磁通密度比较小（见图4b），定性分析时可忽略它，则由Maxwell 应力张量理论可知径向电磁力波为

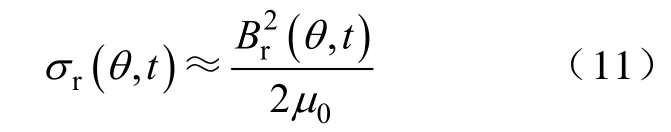
式中σr(θ,t)—径向电磁力波（Pa 或N/m2）；

Br(θ,t)—径向磁通密度波；

μ0—空气磁导率。

由式（11）可见磁通密度波之间相互作用（即相乘）产生电磁力波，这是分析力波产生的理论依据。一个极对数为ma、频率为fa的磁通密度波和另外一个极对数为mb、频率为fb的磁通密度波相互作用产生的力波的阶次和频率分别为ma±mb和fa±fb。

4.2 有限元计算

基于Maxwell 应力张量理论，用等效磁张力（面积力）代替体积力可求出单位面积上的电磁力[1]，它的径向分量为

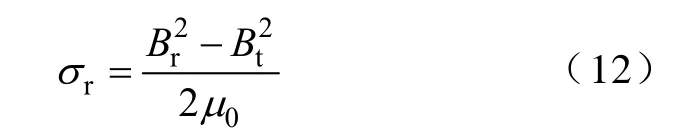
式中σr—径向电磁力（Pa 或N/m2）；

Br—径向磁通密度；

Bt—周向磁通密度。

径向电磁力的空间分布如图6 所示。由图6 可见，在径向磁通密度大的地方径向电磁力也大，径向电磁力在定子齿表面上近似是平的；有个别定子齿表面上径向电磁力存在突变，这是由于该位置存在转子槽口，它受转子旋转的影响；在定子槽位置的径向电磁力很小，即径向电磁力主要作用在齿表面上。气隙圆周方向一点的径向电磁力也随时间变化，如图7 所示，图中给出的是单个定子齿表面周向中心点的电磁力随时间的变化。

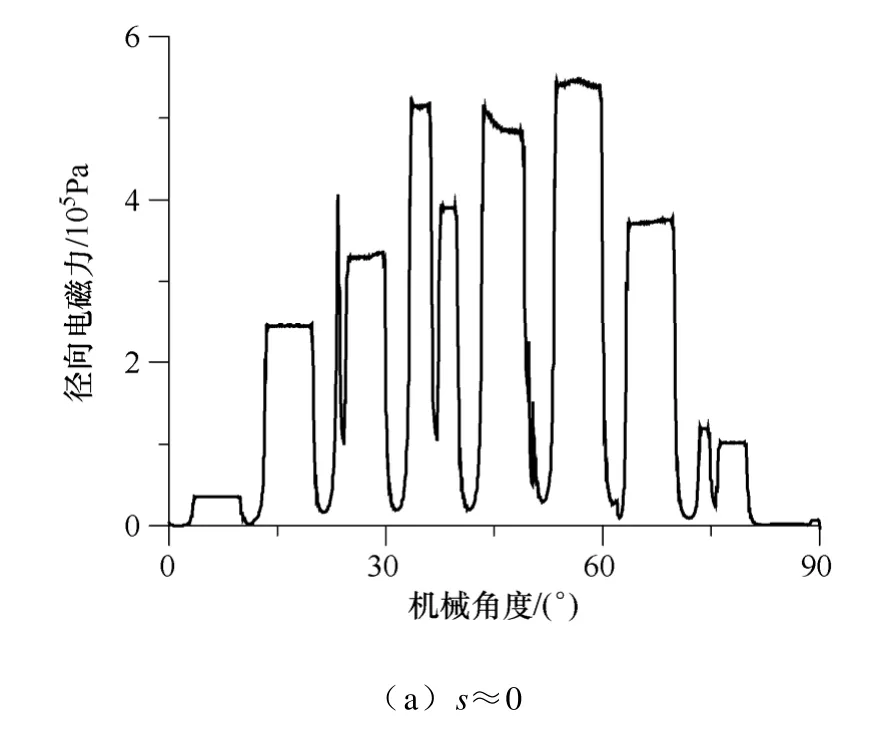
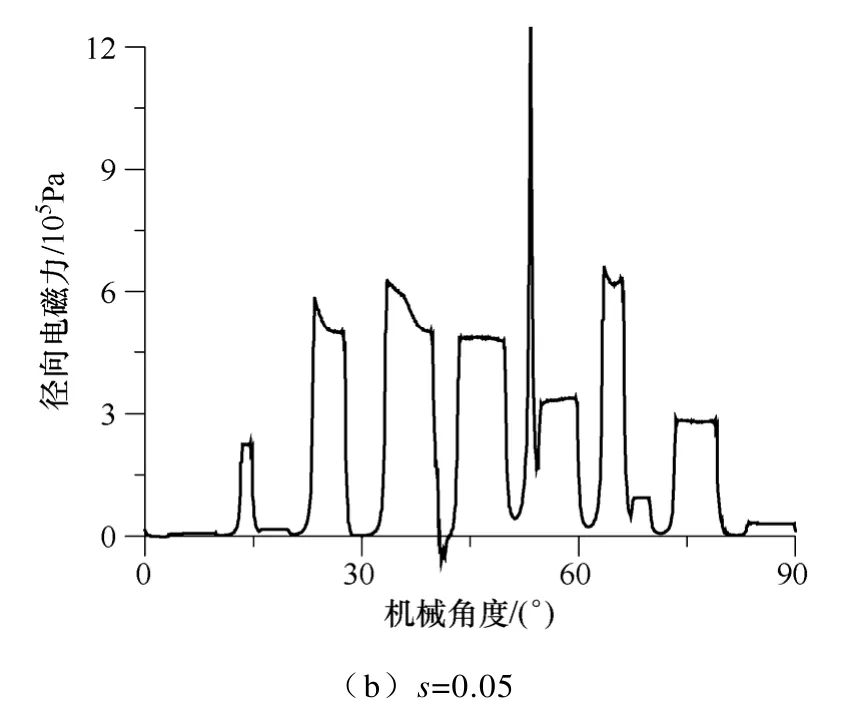
图6 径向电磁力的空间分布Fig.6 Space distribution of radial electromagnetic force

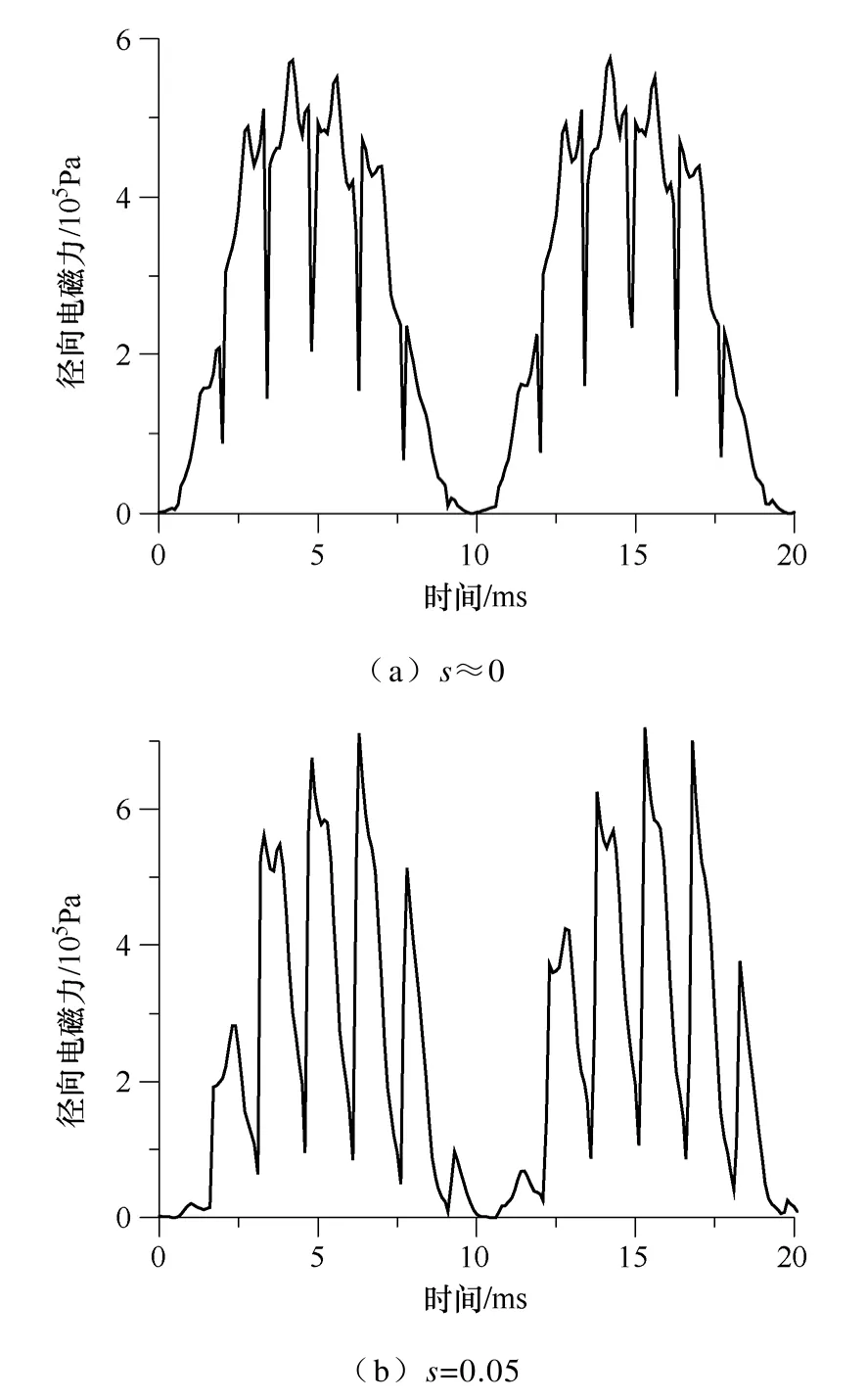
图7 径向电磁力随时间的变化Fig.7 Variation of radial electromagnetic force with time

由图6 和图7 可知，转差率改变，径向电磁力的空间分布和随时间的变化规律均改变，且转差率增大电磁力也增大，从而导致一些力波的频率和幅值发生变化，这是电磁噪声随负载变化的原因。

同磁通密度波一样，径向电磁力波也为行波，旋转谐波理论亦适用于它，即可将时空变化的径向电磁力分解为无穷多个正转或者反转的径向电磁力波，径向电磁力为这些力波的线性叠加，即

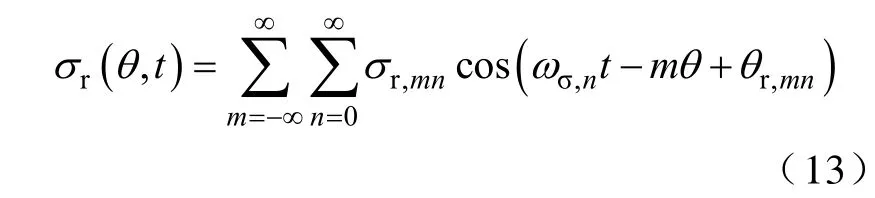
式中m，n—对应空间谐波和时间谐波的次数，均为整数，m的绝对值表示空间阶次，m为正时表示正转波，为负时表示反转波；

θ—空间圆周方向上的机械角度；

t—时间；

σr,mn—幅值；

θr,mn—初始角度；

ωσ,n—时间角频率，ωσ,n=2πfσ,n；

fσ,n—频率。

径向电磁力波的求解方法与径向磁通密度波的求解方法类似，即将时空变化的径向电磁力进行二维离散傅里叶分析可得到式（13）所示的各个力波。以空载稳态为例，阶次低且幅值较大的径向电磁力波见表4，按幅值大小排序列出，阶次为正表示正转波，为负表示反转波。0 阶0Hz的力波表示常值力，它为定转子之间的磁吸力，这个力的幅值很大说明定转子之间磁吸力很强，这是熟知的。

每一个径向电磁力波均可找到两个径向磁通密度波与之对应[2,3]，即两个径向磁通密度波相互作用可产生径向电磁力波。表5 给出了表3 中径向磁通密度波和表4 中几个电磁力波的对应关系。

力波中往往存在同一个空间阶次、几个时间频率的谐波见表4，0 阶、4 阶和8 阶均有几个频率的力波。对时空变化的电磁力进行二维傅里叶分析是求解电磁力波的有效方法。

表4 径向电磁力波Tab.4 Radial electromagnetic force wave

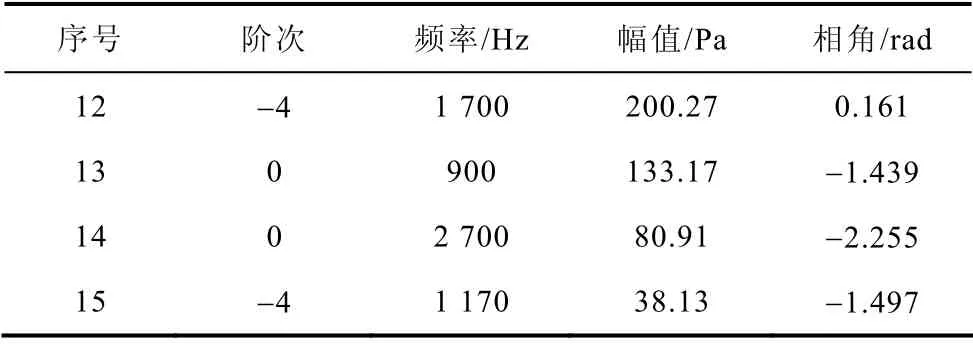
（续）

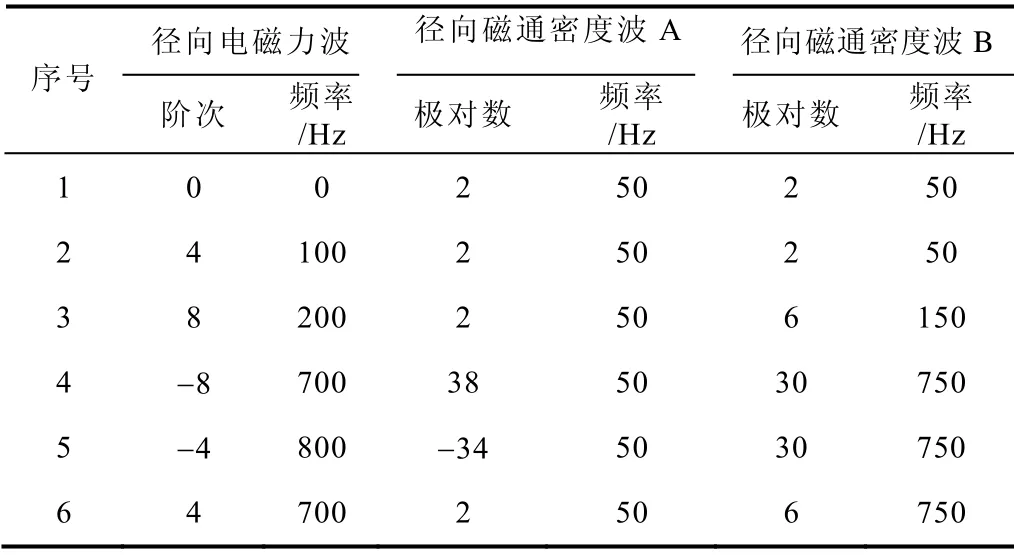
表5 力波和磁通密度波Tab.5 Force wave and flux density waves

4.3 力波的试验验证

电磁力的直接测量十分困难，以下通过电磁噪声频率和力波频率的对比，间接验证力波计算的有效性。m阶力波引起的机械振动振幅几乎与m4成反比[3]，从而只有阶次低且幅值较大的力波才会引起明显的振动和噪声。对小型异步电机，一般阶次小于5的力波才会对电磁噪声有较大的影响。阶次较低电磁力波的频率与电磁噪声频率存在对应关系。实测的空载稳态噪声频谱如图8 所示，测量时电机安装状态为底脚无固定。主要的电磁噪声和电磁力波的对应关系见表6，由表中可看出主要电磁噪声均有相应频率的电磁力波与之对应。

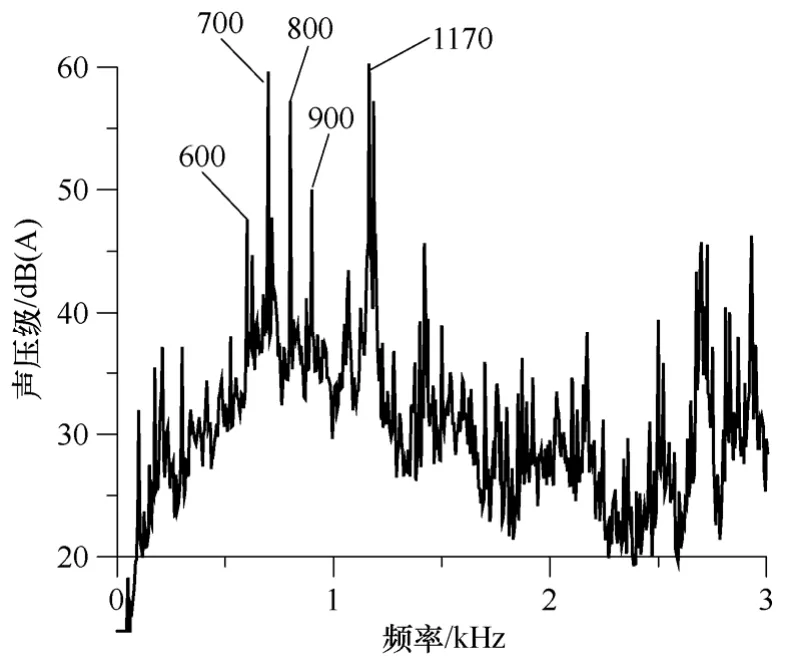
图8 实测的噪声频谱Fig.8 The testing noise spectra

表6 噪声和力波的对比Tab.6 Comparison between noise and force wave

5 结论

基于场路耦合时步有限元数学模型对笼型异步电动机的气隙磁通密度和径向电磁力进行计算。将径向磁通密度和径向电磁力的有限元计算结果进行二维离散傅里叶分析分别得到它们的谐波，这些谐波均为行波，有确定的极对数（或阶次）、频率、幅值、相角和转向。

试验结果表明场路耦合时步有限元模型对电磁量谐波的仿真计算是准确的。实测噪声频谱中各个频率的电磁噪声均有相应频率的径向电磁力波与之对应，验证了本文方法计算径向电磁力波的有效性。

对径向电磁力及其谐波进行计算和分析为电磁噪声分析奠定了基础。

[1]汤蕴璆.电机内的电磁场[M].北京:科学出版社,1998.

[2]Heller B,Hamata V.Harmonic fields effects in induction machines[M].New York:Elsevier Press,1977.

[3]Yang S J.Low noise electrical motors[M].Oxford:Clarendon Press,1981.

[4]Verma S P,Balan A.Determination of radial-forces in relation to noise and vibration problems of squirrel-cage induction motors[J].IEEE Transations on Energy Conversion,1994,9(2):404-412.

[5]Besnerais J Le,Lanfranchi V,Hecquet M,et al.Characterisation of radial vibration force and vibration behaviour of a pulse-width modulation-fed fractional-slot induction machine[J].IET Electric Power Applications,2009,3(3):197-208.

[6]Ramesohl I,Kuppers S,Hadrys W,et al.Three dimensional calculation of magnetic forces and displacements of a clawpole generator[J].IEEE Transations on Magnetics,1996,32(3):1685-1688.

[7]Zhang J J,Wang L L,Zhang H J,et al.Non-linear radial force simulation of switched reluctance motors based on finite element model[C].IEEE Inter.Conf.on Robotics and Biomimetics,2009:21-26.

[8]Zhu Z Q,Xia Z P,Wu L J,et al.Analytical modelling and finite element computation of radial vibration force in fractional-slot permanent magnet brushless machines[C].Inter.Conf.on Electric Machines and Drives,2009:144-151.

[9]Schlensok C,Henneberger G.Calculation of force excitations in induction machines with centric and excentric positioned rotor using 2-d transient FEM[J].IEEE Transations on Magnetics,2004,40(2):782-785.

[10]Martinez Munoz D,Lai J C S.Acoustic noise prediction in a vector controlled induction machine[C].IEEE Inter.Conf.on Electric Machines and Drives,2003,1:104-110.

[11]胡敏强,黄学良.电机运行性能数值计算方法及其应用[M].南京:东南大学出版社,2003.