静止坐标系下无刷双馈感应电机的直接转矩控制

张爱玲 贾文霞 周赞强 王 昕 王建华

（太原理工大学电气与动力工程学院 太原 030024）

1 引言

无刷双馈电机（Brushless Doubly-Fed Machine，BDFM）是近年来研究甚为活跃的一种新型电机，和双馈电机（Doubly Fed Induction Machine,DFIM）相比，由于其无刷而受到人们的青睐。该电机在交流调速系统及变速恒频发电领域有着明显的技术优势。按转子结构的不同BDFM 可以分为无刷双馈磁阻电机（Brushless Doubly-Fed Reluctance Machine，BDFRM）和无刷双馈感应电机（Brushless Doubly Fed Induction Machine,BDFIM）两种，其工作原理、数学模型及工作特性均不同。

BDFM 用作电动机时，可以在恒压频比或恒流控制下开环运行，但电机速度跟随能力较弱，对转矩变化的响应较慢，抗干扰能力不强，因此研究该类电机的控制策略，是增强该电机稳定性、提高动态响应能力使其获得工程实用的关键之一。普通感应电机有许多成功的控制方法，如矢量控制和直接转矩控制等。其中直接转矩控制是继矢量控制之后发展起来的一种新型的控制策略，和前者相比，其最大的优点在于避免了旋转坐标变换，在静止坐标系实现转矩的直接控制，因而使系统结构十分简单，该方法在DFIM 中同样得到成功的应用[1]。但是无刷双馈电机结构和运行的特殊性带来了建模及控制上的复杂性，要得到优化的控制性能，必须将合理的数学模型和控制策略相结合。

在将上述两种控制方法用于无刷双馈电机的控制过程中，国内外学者取得了大量的研究成果。矢量控制方面，文献[2-4]在同步模型基础上，实现了BDFIM 转子磁链定向控制；文献[5]实现了一种基于双同步坐标模型的转子磁链定向控制；文献[6-9]在功率绕组（Power Winding,PW）同步坐标系实现了 PW 磁链定向的BDFIM 发电状态[6,7]及电动 状态[8,9]的控制。上述控制方法尽管采用的数学模型不尽相同，但和异步电机的矢量控制一样，均需进行旋转坐标变换。

直接转矩控制方面，研究成果较多地集中于BDFRM，内容涉及控制方法[10,11]、磁链观测[12]及无编码器控制[13,14]等。相对于BDFRM 和DFIM，BDFIM的直接转矩控制要复杂得多[20]。将该方法用于BDFIM的有文献[15-20]，从控制原理来讲，大体相似，但却是在不同的坐标系实现的。其中文献[15-17]在转子速d-q 坐标系系统中自然避免不了旋转坐标变换；文献[18-20]在控制绕组（Control Winding,CW）静止坐标系数学模型的基础上研究了BDFIM 直接转矩控制，在这组数学模型中需要将 PW的电压、电流等旋转变换到 CW，从而和 CW 具有相同的频率。系统中电磁转矩的观测方法为

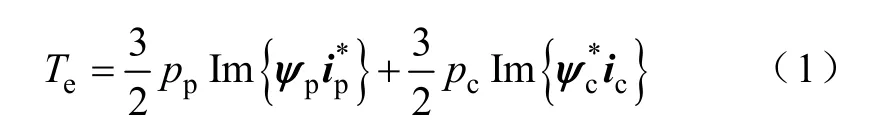
式中ψp——PW 磁链矢量；

ic——CW 电流矢量。

上述各种直接转矩控制方法尽管采用的数学模型不尽相同，但是均需进行旋转坐标变换，使系统结构复杂；而且由于旋转变换矩阵中用到转子转速，因此使系统控制精度受到转速测量误差的影响，并未保留异步电机直接转矩控制的优点。此外文献[20]用到较多的电机参数，且只给出某一转速下负载阶跃变化时的试验结果，而调速性能无疑是重要的性能之一，该文并未给出。

本文提出一种静止坐标系下BDFIM的直接转矩控制方法。推导了电磁转矩的计算方法，即分别在CW 和PW 各自的静止坐标系观测其磁链、电 流，进而计算转矩；构建了同时适用于亚同步及超同步电动运行状态的开关表。本文所提方法无需旋转坐标变换，系统所需参数仅仅为两个定子绕组的电阻。除了需要多观测一个定子绕组的电压电流之外，控制系统结构和异步电机直接转矩控制系统一样简洁明了。亚同步及超同步等不同转速下样机的稳态及动态实验结果表明所提控制方法的有效性。

2 BDFIM 在转子速d-q 坐标系的数学模型

BDFIM 在转子速d-q 坐标系的数学模型[21,22]由电压方程（2）、磁链方程（3）～方程（5）、转矩方程（6）以及运动方程（7）组成。

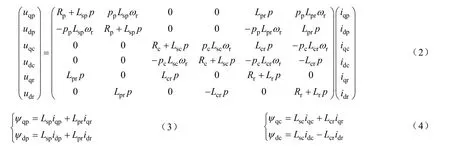
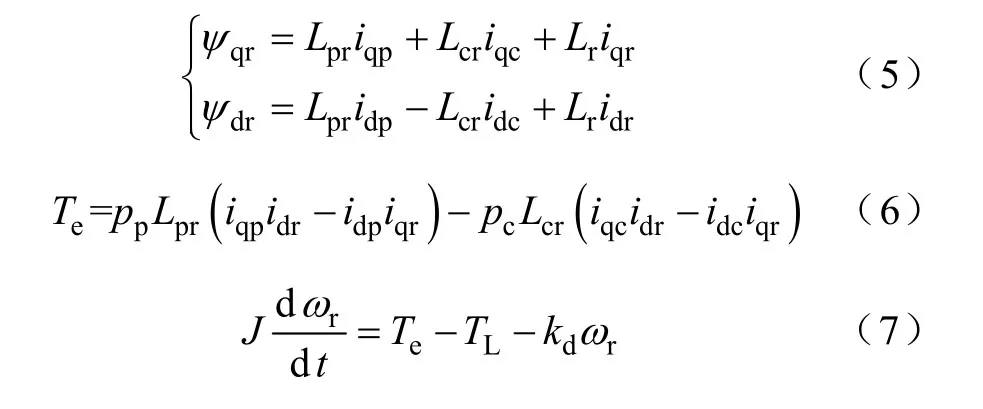
式中

uqp,udp,uqc,udc,uqr,udr——PW、CW 和转子绕组电压的d、q 分量；

iqp,idp,iqc,idc,iqr,idr——PW、CW 和转子绕组电流和小q 分量；

p——微分算子；

ωr——转子机械角速度；

Rp,Rc,Rr,Lsp,Lsc,Lr——PW、CW、转子绕组的电阻和自感；

Lpr,Lcr——PW、CW 与转子绕组的互感；

ψqp,ψdp,ψqc,ψdc,ψqr,ψdr——PW、CW 和转子绕组磁链的d、q 分量；

pp,pc——PW 和CW的极对数；

J——转动惯量；

Te——电磁转矩；

TL——负载转矩；

kd——阻尼系数。

下标p、c、r 分别表示PW、CW 及转子绕组的有关变量。

利用式（6）计算电磁转矩时，需要先将PW 和CW的有关变量变换到各自的αβ 坐标系，再旋转变换到转子速d-q 坐标系。PW 和CW的旋转变换矩阵C1、C2分别为

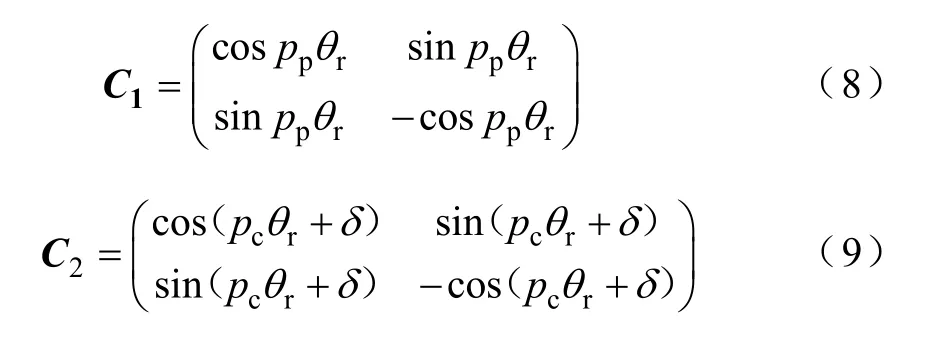
例如，已知PW 电流在其静止 αβ 坐标系的分量iαp、iβp，则

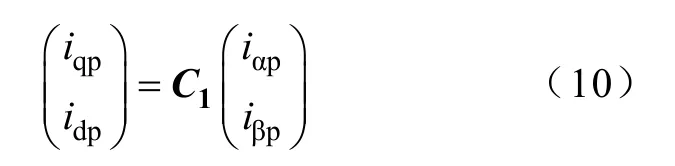
式中δ——功率绕组A 相与控制绕组a 相轴线之 间的机械夹角；

θr——转子旋转的机械角[21]，用式（11）计 算。

以上坐标变换方法同样适用于磁链和电压。由于转子电流不能实测，用式（6）计算电磁转矩时，需要首先观测PW（或CW）的磁链，然后根据磁链方程（3）（或方程（4））间接计算转子电流[17,23]。系统实现时，由于参数的影响使转子电流计算不准以及由于转子角速度的测量误差因PW 和CW 旋转变换角的不同而放大了不同的倍数，致使转矩观测结果不稳定。为了避免上述问题，可以分别观测PW和CW的磁链，用磁链方程（3），方程（4）置换掉式（6）中的转子电流。

由磁链方程（3），得

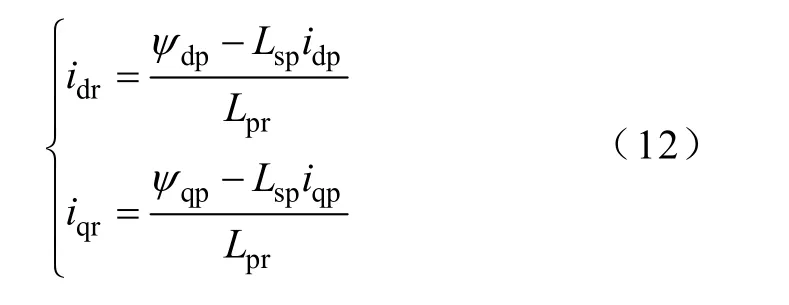
由磁链方程（4），得

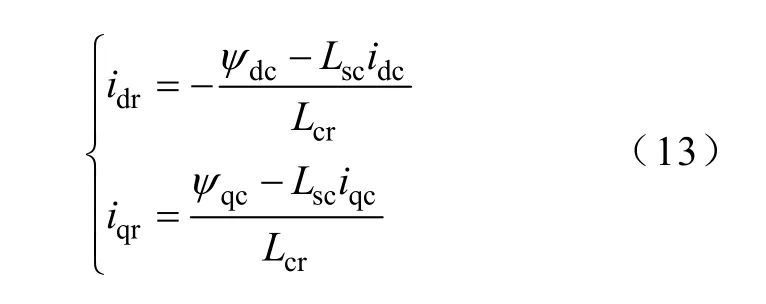
将式（12）和式（13）分别代入转矩方程（6）的第一和第二项，化简后得

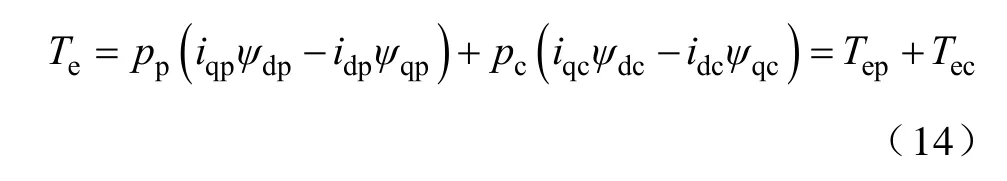
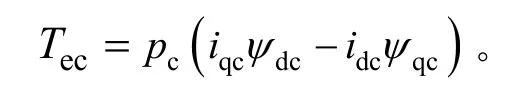
式中，Tep、Tec分别为PW 和CW 产生的转矩，可以由两个绕组各自的磁链及电流计算，虽然避免了转子电流的计算，但旋转坐标变换是必须的。

3 静止坐标系下电磁转矩的计算

将式（14）中的Tep、Tec根据式（8），式（9）分别旋转变换到PW 和CW 各自的静止坐标系，Tep可以写成

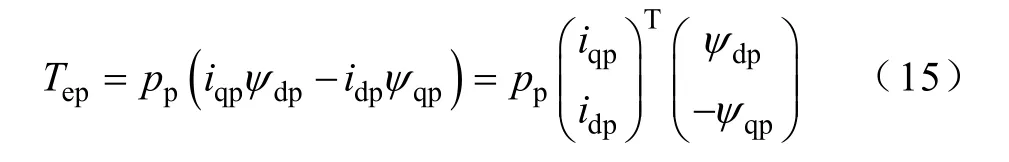
由式（10），得

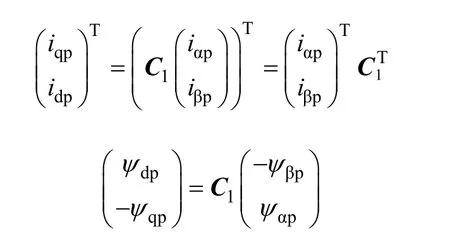
因此式（15）可以写为

式中ψαp，ψβp——PW 磁链的αβ 分量。

式（16）即为PW 静止坐标系下该绕组电磁转矩的表达式，和异步电机在 αβ 坐标系电磁转矩的表达式相似。同理可得CW 静止坐标系下该绕组电磁转矩的表达式为

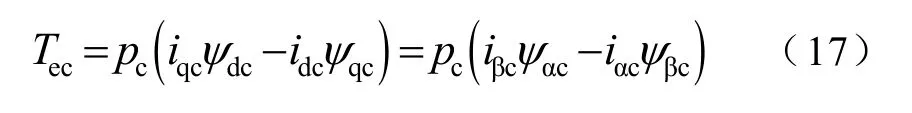
将式（16）和式（17）相加即为BDFIM的总转矩

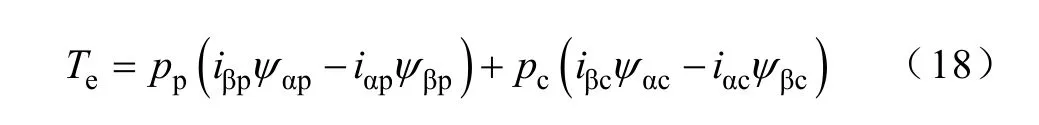
式中iαc,iβc——CW 电流的αβ 分量。

ψαc,ψβc——CW 磁链的αβ 分量。

式（18）表明，只需观测PW 和CW 在其各自静止坐标系磁链、电流的αβ 分量，即可在各自静止坐标系下实现无刷双馈电机的转矩观测，而磁链和电流 αβ 分量的观测只需要一次从 ABC-αβ 坐标系的三相/两相静止坐标变换。

4 PW 及CW的磁链观测

式（18）中CW 及PW的磁链采用u-i模型式（19）观测，所用方法相同，不再区分下标。

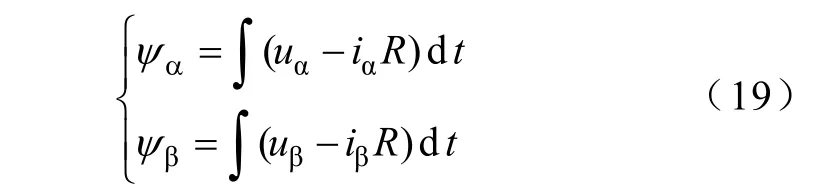
式中uα，uβ——两个定子绕组电压在其各自静止

αβ 坐标系的分量；

R——各自的电阻。

为了解决积分漂移问题，采用了带正交非线性补偿的u-i模型[24]。系统运行中需要在每个采样周期内测量PW 电压、电流以及CW的电流。CW 由逆变器供电，其端电压可以根据每个采样周期的开关状态和逆变器直流母线电压进行重构[25]，再通过坐标变换得到 αβ 分量。

5 BDFIM 直接转矩控制系统

5.1 BDFIM 直接转矩控制系统原理

BDFIM 直接转矩控制系统的结构如图1 所示，PW 接380V 工频电源不可控，CW 由变流器供电。图1 中n*、Te*、ψ*c分别为转速、转矩和CW 磁链的给定值，n、Te、ψc为对应的反馈值，iac、ibc、icc、iap、ibp、icp、uac、ubc、ucc、uap、ubp、ucp分别为控制绕组和功率绕组A 相、B 相和C 相的电流电压，uαp、uβp、uαc、uβc分别为PW 和CW 电压在其静止坐标系的αβ 分量，ΔT′、Δψ′分别为转矩和磁链增量且ΔT′=Te*-Te，Δψ′=ψ*c-ψc。

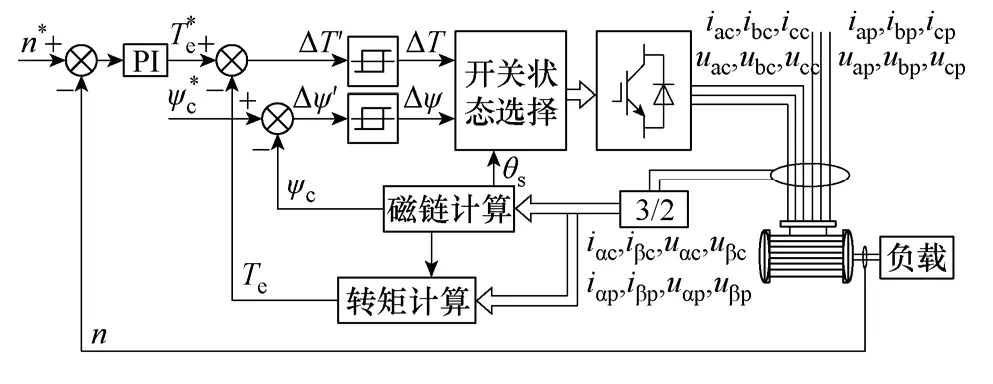
图1 直接转矩控制系统结构框图Fig.1 Schematic of the proposed DTC control system

系统运行时在每个采样周期内首先根据第4 节所述方法观测磁链，其次用式（18）计算电磁转矩，然后将计算所得的ψc、Te分别与他们的给定值进行比较（速度调节器的输出为转矩的给定值Te*），比较差值经过各自的滞环比较器输出ΔT、Δψ，结合ψc所在的扇区（即位置角θs，由ψαc、ψβc计算）根据开关表确定所需的电压矢量，控制逆变器输出电压的频率、幅值及相位，达到控制BDFIM 转速、运行状态、功率因数的目的。

综上所述，BDFIM 直接转矩控制系统的结构和异步电机一样简洁明了，系统用到的参数只有定子电阻，但是开关表和异步电机不同。

5.2 开关表

异步电机中零矢量的作用是减小转矩，但由于无刷双馈电机工作原理的特殊性，在双馈运行的两种状态零矢量对转矩的作用并不一致[19]，超同步运行状态零矢量的作用和异步电机一样，而亚同步运行状态零矢量使转矩增大。因此，开关表的设计有别于异步电机直接转矩控制系统。考虑到两种运行状态开关表的通用性，不再使用零矢量，系统的开关表见表1。

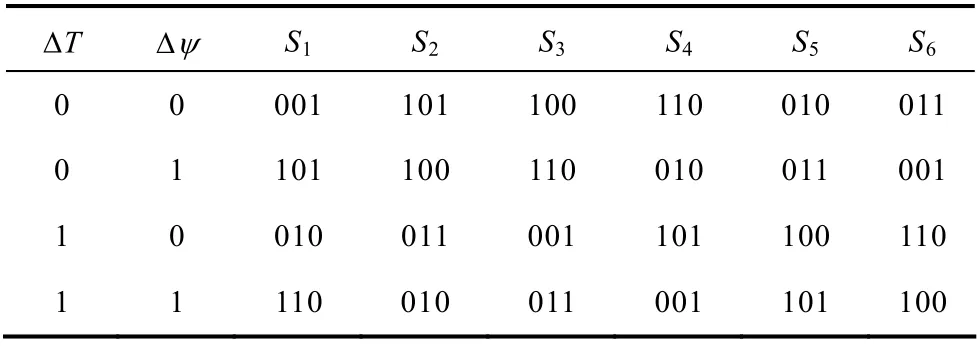
表1 开关表Tab.1 Switch table

表1 中当ΔT′≥εT时，ΔT=1，表示需要增加转矩，否则，ΔT=0，表示需要减小转矩；同理，当Δψ′≥εψ时，Δψ=1，否则，Δψ=0。εT、εψ分别为转矩和磁链滞环比较器的环宽，S1～S6为磁链所在扇区值，由ψαc、ψβc计算。

6 实验结果

为了验证本文所提方法的正确性，在交流电机实验平台上对BDFIM 样机进行了相关实验。样机采用笼型转子，如图2 所示，4 组同心式短路线圈，每组5 个短路环，其余参数见表2。试验平台如图3所示，直流发电机作为BDFIM的负载，扭矩传感器用来测量BDFIM的输出转矩，转速使用OMRON增量式E6C2—CWZ6C 光电编码器测量。

图2 样机转子Fig.2 The prototype rotor

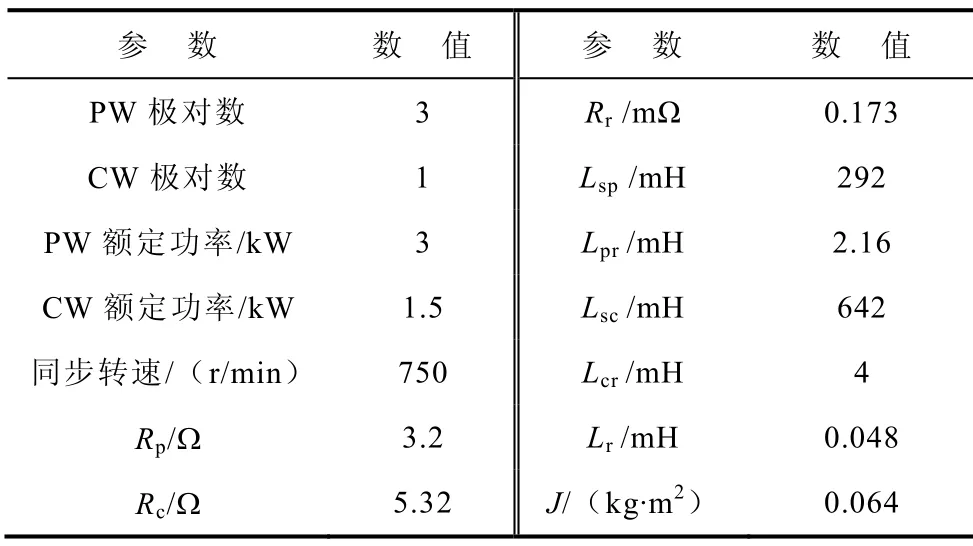
表2 样机参数Tab.2 Prototype parameters

图3 实验装置Fig.3 Experimental setup

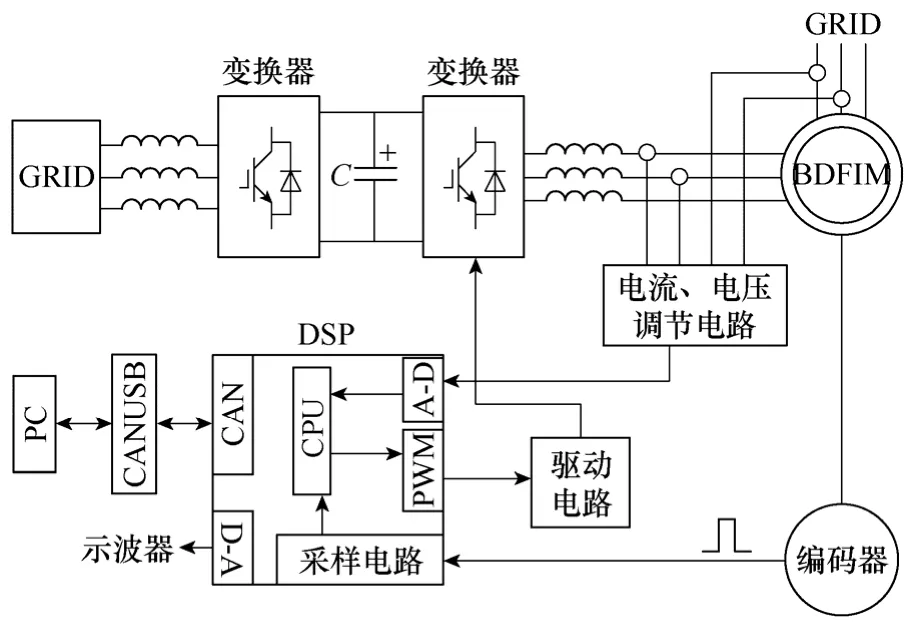
图4 变流器结构示意图Fig.4 Schematic diagram of the converter

实验中功率绕组接380V 工频电源，控制绕组接双PWM 变流器，图4 为其结构示意图。两个变流器的控制系统相似，图中只画出电机侧变流器控制系统的示意图。数字信号处理芯片（Digital Signal Processor，DSP）（TMS320LF2407A）是控制系统的核心，其通信接口CAN 及PC的USB 接口通过USBCAN 接口卡相连，实现DSP 与PC 之间的数据交换。系统采样周期Ts=280μs，CW 磁链给定。实验结果如图5～图11 所示，图中ic、ip分别为CW、PW 电流，由霍尔电流传感器测量；nr为电机转速，ψαc为CW 磁链的α 分量，Te为电磁转矩。nr、ψαc、Te分别根据采样及计算值从系统的D-A 口输出到示波器。

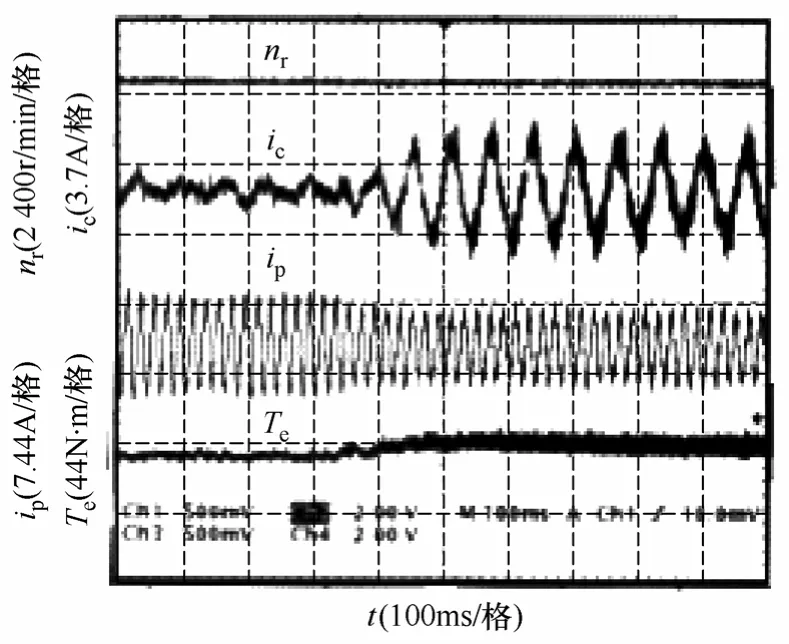
图5 转速525r/min 时突加负载时转速、控制绕组 电流、功率绕组电流、电磁转矩波形Fig.5 Experimental results for the torque change at 525r/min

图6 转速525r/min 时突减负载时转速、控制绕组 电流、功率绕组电流、电磁转矩波形Fig.6 Experimental results for the torque change at speed of 525r/min

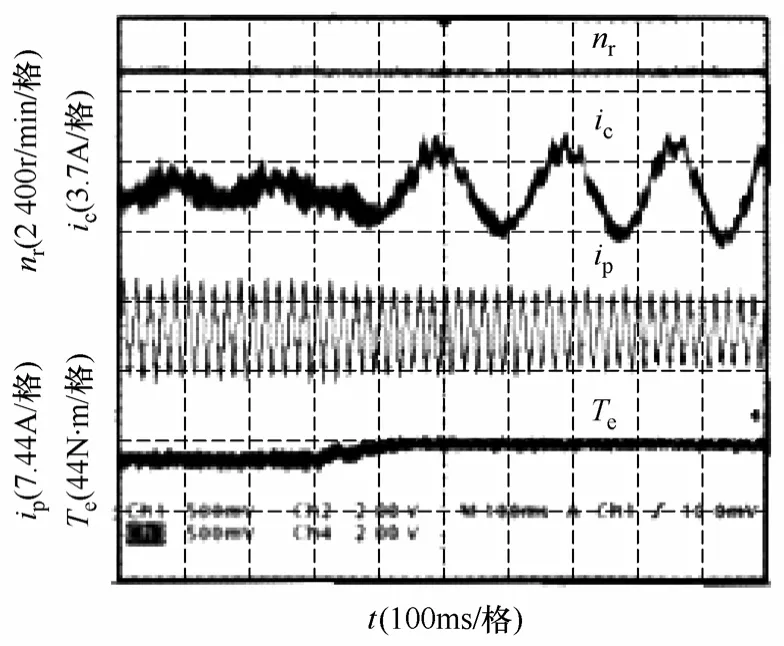
图7 转速850r/min 时突加负载时转速、控制绕组 电流、功率绕组电流、电磁转矩波形Fig.7 Experimental results for the torque change at speed of 850r/min

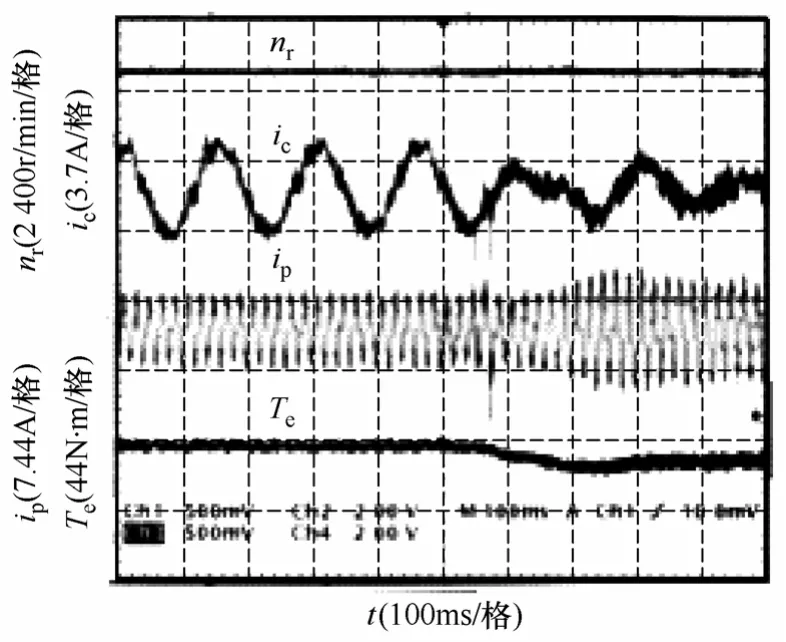
图8 转速850r/min 时突减负载时转速、控制绕组 电流、功率绕组电流、电磁转矩波形Fig.8 Experimental results for a step torque decrease at speed of 850r/min

6.1 负载突变时的动态性能

图5～图8 为稳定运行状态下负载突变时转速、CW 和PW 电流以及电磁转矩的实验结果。其中图5 为亚同步525r/min 系统空载运行时突然增加负载使电磁转矩达到 8.1N·m 时的实验结果，图 6 为525r/min 时突减负载到空载的实验结果，图7、图8为超同步850r/min 运行状态负载突变的实验结果。从以上实验结果可见：

（1）无论是超同步还是亚同步运行状态，在负载扰动前后及动态过程中转矩的观测值跟随运行状态的变化而变化，观测结果稳定准确，表明了本文所提转矩观测方法的正确性。

（2）在经受负载扰动后，转速的动态变化很小，系统运行稳定。

（3）由图5～图8 可见，负载增加（减小）时ip减小（增加），这是由于试验中保持不变，致使PW 功率因数随负载变化所致。式（19）中略去电阻压降，当保持ψc不变时，相当于保持控制绕组电压不变。由BDFIM 工作原理，负载变化时，PW 功率因数会发生相应的变化。理论分析及实验结果表明，取不同的数值且保持不变，当负载变化时ip的变化规律有所不同。调节ψc的给定值，控制PW的无功功率为期望值是本文下一步解决的问题。

6.2 调速时的动态性能

图9、图10 为调速时的转速、CW 和PW 电流以及CW 磁链的波形。其中图9 为超同步850r/min到亚同步525r/min 调速的实验结果，图10 为亚同步到超同步调速的实验结果，图11 为系统稳定运行时CW 及PW的电流波形。

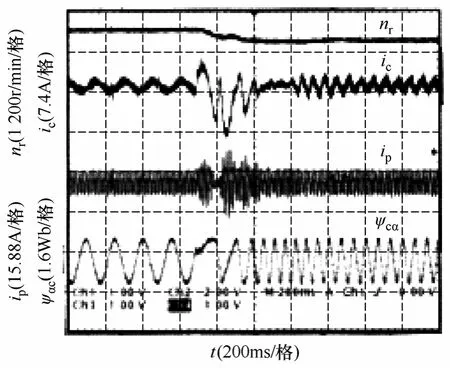
图9 从850r/min 至525r/min 调速时转速、控制 绕组电流、功率绕组电流、控制绕组磁链波形Fig.9 Experimental results for the speed changeing from 850r/min to 525r/min

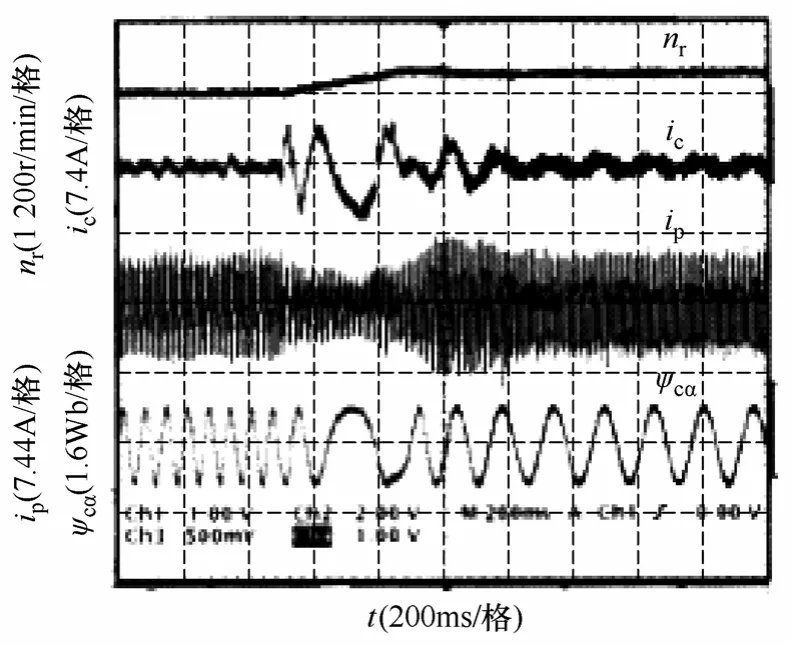
图10 从525r/min 至850r/min 调速时转速、控制 绕组电流、功率绕组电流、控制绕组磁链波形Fig.10 Experimental results for the speed change from 525r/min to 850r/min

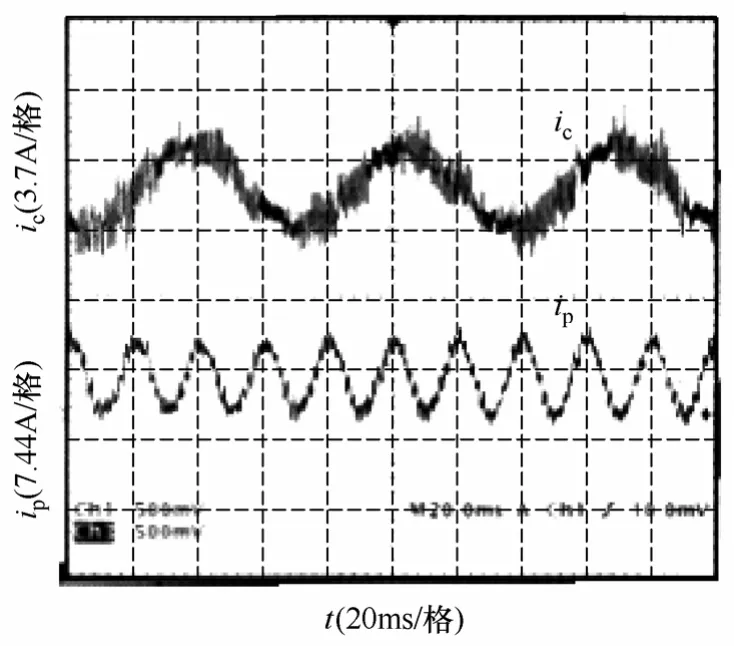
图11 525r/min 时控制绕组电流、功率绕组电流波形Fig.11 Current waveform at 525r/min

从以上实验结果可见：

（1）在速度变化的动态过程中，尤其是在跨越同步速时系统转速跟随给定值平稳变化、电流在经过短暂的调节后达到稳定。

（2）磁链的幅值始终保持在给定值附近，表明磁链观测及控制的正确性和稳定性。

7 结论

本文提出的静止坐标系下BDFIM的直接转矩控制方案以及转矩观测方法，避免了旋转坐标变换、电机参数及转速观测误差对计算结果的影响，从而使BDFIM 直接转矩控制系统对参数的鲁棒性强，系统结构和异步电机一样简单。亚同步和超同步等不同转速下的速度跟随性能及抗负载扰动性能的试验结果表明所提控制方法的有效性和正确性。实验结果同时表明，和速度开环系统相比，抗负载扰动能力、速度跟随性能及系统稳定性提高，因此本文所述方法是一种适合于无刷双馈电机的控制方法。但是从图5～图8 及图11的实验结果来看，控制绕组电流及转矩脉动偏大，这是本文下一步解决的问题。

[1]Abad G,Rodríguez M A,Poza J.Two level VSC based predictive direct torque control of the doubly fed induction machine with reduced torque and flux ripples at low constant switching frequency[J].IEEE Trans on Power Electronics,2008,23(3):1051-1061.

[2]章玮.无刷双馈电机系统及其控制研究[D].杭州:浙江大学,2001.

[3]Zhou D,Spee R,Gerald C Alexander.Experimental evaluation of a rotor flux oriented control algorithm for brushless doubly-fed machines[J].IEEE Trans on Power Electronics,1997,12(1):72-78.

[4]黄守道,王耀南,黄科元,等.无刷双馈电机转子磁场定向控制策略的研究[J].电工技术学报,2002,17(2):34-38.Huang Shoudao,Wang Yaonan,Huang Keyuan,et al.Study of the control strategy on rotor field orientation for brushless doubly-fed machine[J].Transactions of China Electrotechnical Society,2002,17(2):34-38.

[5]黄守道.无刷双馈电机的控制方法研究[D].长沙:湖南大学,2005.

[6]Shao Shiyi,Abdi Ehsan,Barati Farhad,et al.Stator-flux-oriented vector control for brushless doubly fed induction generator[J].IEEE Transactions on Industrial Electronics,2009,56(10):4220-4228.

[7]Shao Shiyi,Abdi Ehsan,Richard McMahon,et al.Vector control of the brushless doubly-fed machine for wind power generation[C].IEEE International Conference on Sustainable Energy Technologies,2008:322-327.

[8]Poza Javier,Oyarbide Estanis,Roye Daniel,et al.New vector control algorithm for brushless doubly-fed machines[C].Industrial Electronics Conference,2002:1138-1143.

[9]Poza J,Oyarbide E,Sarasola I,et al.Vector control design and experimental evaluation for the brushless doubly fed machine[J].IET Electric Power Applications,2009,3(4):247-256.

[10]Yu Jian,Jovanovic Milutin G,Levi Emil.Simulation of direct torque control of brushiess doubly fed reluctance machines[C].37th International Universities Power Engineering Conference,2002:699-703.

[11]Jovanovic Milutin G,Yu Jian,Levil Emil.Direct torque control on a brushless doubly fed reluctance machine[C].39th International Universities Power Engineering Conference,2004:587-590.

[12]Jovanovic M G,Yu J,Levi E.Real-time implementation of direct torque control scheme for brushless doubly-fed reluctance motors[C].Second International Conference on Power Electronics,Machines and Drives,2004:752-757.

[13]Jovanovic M G,Yu J,Levi E.Jovanovic Milutin G,Yu,Jian,Levi,Emil,et al.Encoderless direct torque controller for limited speed range applications of brushless doubly fed reluctance motors[J].IEEE Transactions on Industry Applications,2006,42(3):712-722.

[14]Jovanovic M G,Ahmed M M R.Sensorless speed control strategy for brushless doubly-fed reluctance machines[C].International Electric Machines and Drives Conference,2007:1514-1519.

[15]Brassfield William R,Spee Rene,Habetler Thomas G,et al.Direct torque control for brushless doubly-fed machines[J].IEEE Transactions on Industry Applications,1996,32(5):1098-1104.

[16]杨俊华,吕惠子,吴捷,等.基于波波夫超稳定性的无刷双馈电机直接转矩控制[J].中国电机工程学报,2009,29(15):107-113.Yang Junhua,Lü Huizi,Wu Jie,et al.Direct torque control strategy for brushless doubly-fed machines based on popov hyperstability theory[J].Proceedings of the CSEE,2009,29(15):107-113.

[17]张爱玲,张洋.基于转矩预测控制的无刷双馈电机直接转矩控制系统[J].电机与控制学报,2007,11(4):326-330.Zhang Ailing,Zhang Yang.Direct torque control for brushless doubly-fed machine based on torque predict control strategy[J].Electric Machines and Control,2007,11(4):326-330.

[18]Sarasola I,Poza J,Rodriguez M A.Direct torque control for brushless doubly-fed induction machines[C].IEEE International Electric Machines and Drives Conference,2007:1496-1501.

[19]Sarasola Izaskun,Poza Javier,Rodríguez Miguel Ángel,et al.Predictive direct torque control for brushless doubly fed machine with reduced torque ripple at constant switching frequency[C].IEEE International Symposium on Industrial Electronics,2007:1074-1079.

[20]Izaskun Sarasola,Javier Poza,Miguel A Rodriguez,et al.Direct torque control design and experimental evaluation for the brushless doubly fed machine[J].Energy Conversion and Management,2011,52(2):1226-1234.

[21]Boger M S,Wallace Alan K,Spee Rene,et al.General pole number model of the brushless doubly-fed machine[J].IEEE Transactions on Industry Apllication,1995,31(5):1022-1028.

[22]Li Ruqi,Wallace Alan K,Spee Rene,et al.Two-axis model development of cage-rotor brushless doubly-fed machines[J].IEEE Transactions on Energy Conversion,1991,6(3):453-461.

[23]刘晓鹏.无刷双馈电机变频调速系统的研究[D].太原:太原理工大学,2005.

[24]贾洪平,贺益康.一种适合DTC 应用的非线性正交反馈补偿磁链观测器[J].中国电机工程学报,2006,26(1):101-105.Jia Hongping,He Yikang.A new nonlinear perpendicular flux observer with compensation feedback suitable for DTC application[J].Proceedings of the CSEE,2006,26(1):101-105.

[25]王小明,王玲.电动机的DSP 控制——TI 公司DSP应用[M].北京:北京航空航天大学出版社,2004.