无轴承开关磁阻全周期发电机输出功率的建模与优化控制

庄 铮 邓智泉 曹 鑫 赵丽丹

（南京航空航天大学自动化学院电气工程系 南京 210016）

1 引言

开关磁阻电机由于其结构简单、容错能力强以及在恶劣环境下的适应能力而受到电工界的广泛关注，并已在航空航天、民用、军事等领域得到了广泛应用[1,2]。然而，由于机械加工、装配等问题，将会引起作用于SRM 转子上的径向力的不对称分布，这也是造成SRM 振动和噪声问题的根源。无轴承开关磁阻电机则是通过主动控制定、转子间的不对称径向磁拉力，为转子提供可控的径向悬浮力，最终实现电机高速运行时的悬浮控制。

日本学者于 20 世纪 90年代开始对双绕组BSRM 从理论到实验进行了深入研究，包括建立电机的数学模型，设计电机的控制策略。国内目前从事BSRM 研究的有南京航空航天大学、江苏大学、北京交通大学、华中科技大学等[3-13]。在对双绕组BSRM 研究相对完善之后，单绕组BSRM 成为另一个无轴承技术的研究方向。NASA的B.B.Choi、德国开姆尼茨工业大学L.Chen 和中国台湾淡江大学S.M.Yang 等人分别研究了不同结构的单绕组BSRM 及其控制策略[14,15]。

目前的研究主要集中在 BSRM的电动运行状态，由于SRM 起动/发电功能的优越性，无轴承开关磁阻发电机作为电机的另一种运行模式理应受到相当的关注，而发电运行的研究主要处于前期探索阶段。无轴承开关磁阻发电机高速运行时转轴与辅助轴承无机械接触，有效解决了高速电机轴承磨损发热的问题，因此适用于轴承难以更换的深海、航空领域。文献[16]针对无轴承开关磁阻分时发电系统进行了一些基础研究，主要分析了无轴承开关磁阻电机单相导通数学模型和能量转换关系。文献[17]提出了一种无轴承开关磁阻电机全周期发电模式，推导了相应的数学模型并提出一种简单的控制策略。文献[18]在此基础上，完成了无轴承开关磁阻全周期发电机的电机结构参数设计。

普通开关磁阻发电机由于其分时发电的模式，输出功率受到限制。无轴承开关磁阻全周期发电机尝试利用单独的一套绕组励磁以提高输出功率。由于励磁绕组与发电绕组耦合严重，分析能量转换关系和输出功率相对困难，文献[17]只是提出了一种简单的控制策略，并未对输出功率进行优化。为进一步提高输出功率，本文致力于研究无轴承开关磁阻发电机输出功率的建模和优化控制。基于此，首先推导了发电电流的分段解析式，通过电流解析式探析励磁区间对发电机输出功率的影响，提出输出功率优化控制的方法，并在试验样机上得到验证。

2 悬浮发电原理

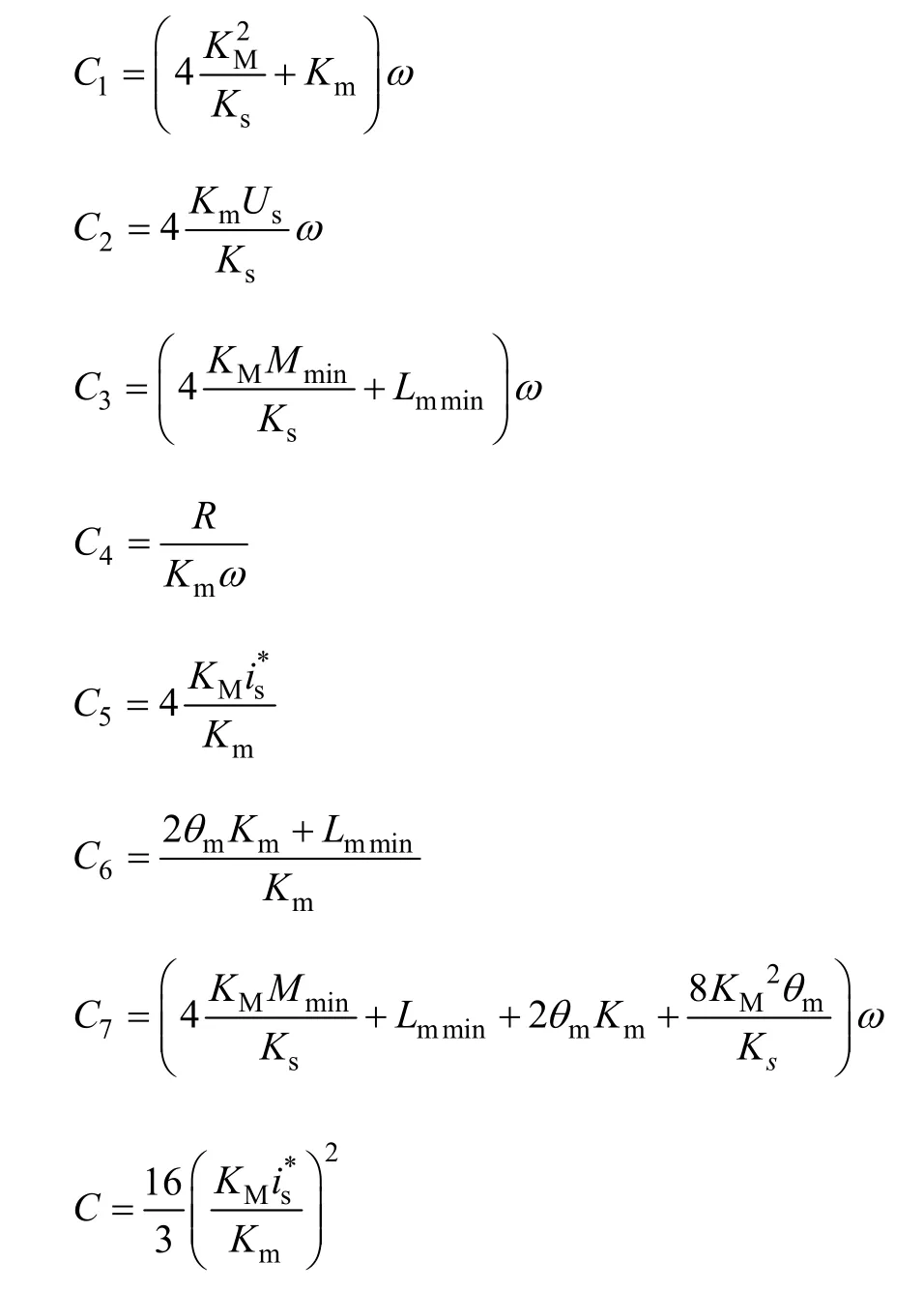
图1a 为12/8 结构的无轴承开关磁阻全周期发电机的绕组结构图。定子齿有两套集中绕组，分别为悬浮绕组和主绕组，这里的主绕组作为发电绕组，悬浮绕组作为励磁绕组。如图1b 所示，每极悬浮绕组均由不对称半桥单独控制；主绕组一相四极串联整流。为简化悬浮控制，使三相悬浮绕组轮流导通，即各自导通15°。通过调节位于径向相对位置上的两极悬浮绕组的电流大小，使其对应的气隙磁通密度不平衡分布，从而产生作用于转子的不对称径向磁拉力，通过对该径向力和悬浮绕组电流的闭环控制，即可实现悬浮电机转子的目的。

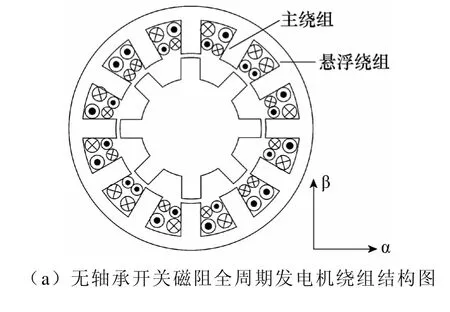
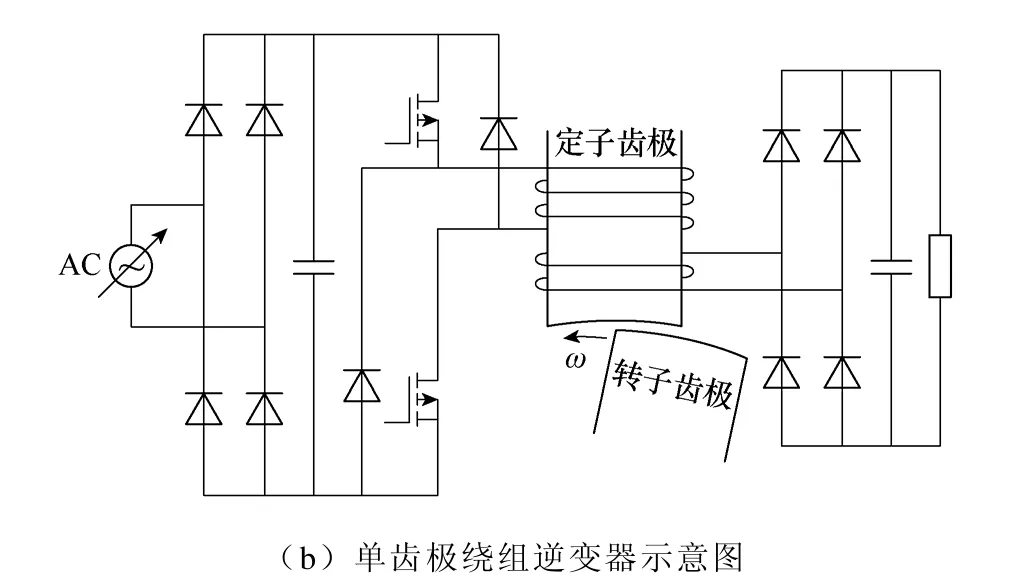
图1 无轴承开关磁阻全周期发电机原理示意图Fig.1 Schematic view of configuration of FPBSRG system

由于定子两套绕组相互耦合，悬浮绕组开通时，主绕组会产生反向感应电流阻碍磁通变化。悬浮绕组关断时，励磁电流在反向电压作用下迅速减小，为阻碍主磁通突变，主绕组电流方向由负变正，幅值迅速增大直至悬浮绕组电流降为零。此后，与普通开关磁阻发电机类似，发电绕组进入续流发电阶段。其典型的电流波形如图2 所示。因此，无轴承开关磁阻全周期发电机在实现悬浮的同时，在相导通周期内均有输出电能。

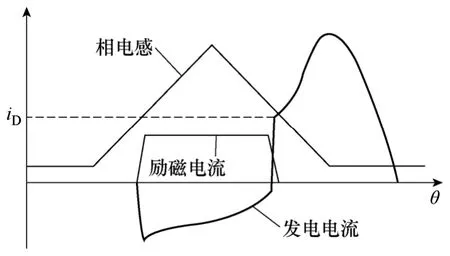
图2 典型电流波形Fig.2 Typical current waveforms

3 输出功率的建模分析和优化

3.1 相电流解析

无轴承开关磁阻全周期发电机悬浮绕组励磁区间对发电机输出功率有很大影响[19]。但由于两套绕组相互耦合，分析相对困难。通过引入相电流解析，可以从理论上分析励磁开通、关断角与输出功率的关系，从而为优化励磁控制策略提供依据。

为简化分析，不考虑磁路饱和，不计漏磁和边缘散磁，电感为近似三角形分布，忽略二极管、开关管和绕组内阻压降，悬浮绕组斩波阶段近似为一条直线，转速为常数，发电电压已到达稳定并不考虑悬浮力。在一相中，设四极串联的主绕组自感最大值为Lmmax，最小值为Lmmin，上升率为Km，一极的悬浮绕组自感相应项依次为Lsmax、Lsmin、Ks，主绕组与悬浮绕组互感相应项依次为Mmax、Mmin、KM。

图3 为相电流解析角度示意图。定义角度起点为相电感初始上升点，θm、θ3分别为电感到达最大值和最小值时对应的角度。悬浮绕组开通区间为[θon，θoff]；励磁电流到达电流给定值的角度为θ1；励磁 电流下降到零的角度为θ2。发电电流下降到零的角度为θ4。

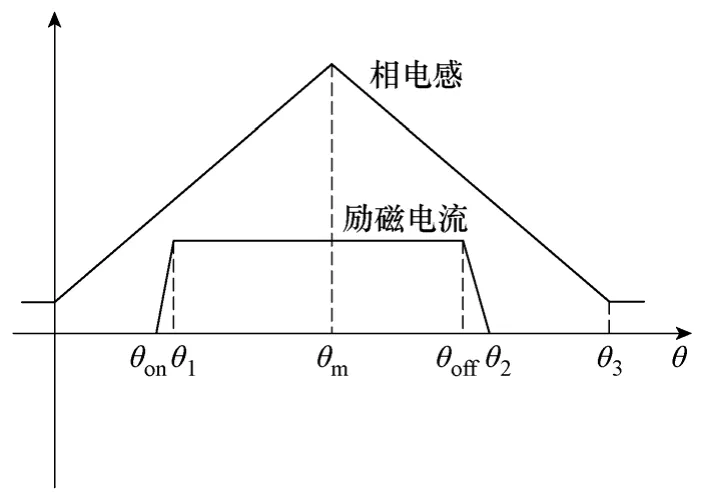
图3 角度示意图Fig.3 Schematic diagram of angles

根据以上假设和定义，悬浮绕组和主绕组的电压方程可表示为

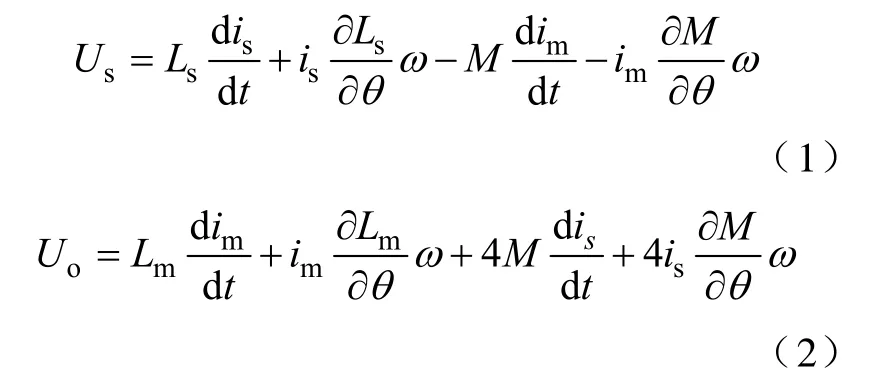
式中Us、Uo—悬浮绕组和主绕组电压；

is、im—悬浮绕组和主绕组电流；

Lm、Ls、M—主绕组自感、悬浮绕组自感和两 套绕组互感；

ω—发电机转速。

根据绕组电压方程，主绕组电流可分段表示为

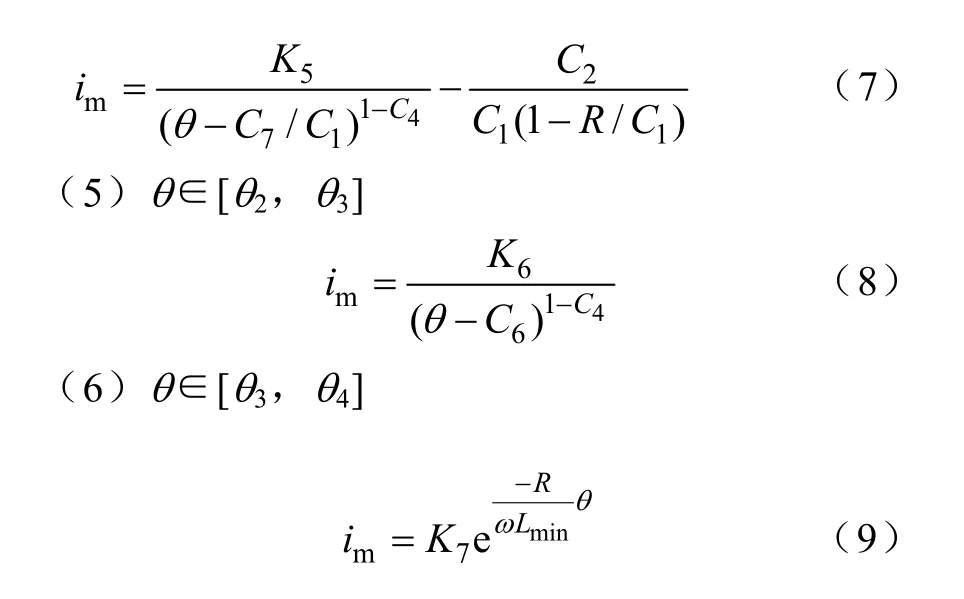
式中，C1～C7为与角度无关的常量，具体数值见附录；K1～K5是根据每段电流边界条件计算得到的波形系数；R为发电机输出负载。

3.2 励磁区间输出功率分析

在励磁区间[θon，θoff]内，悬浮绕组导通，主绕组感应发电。在励磁区间主绕组输出功率为

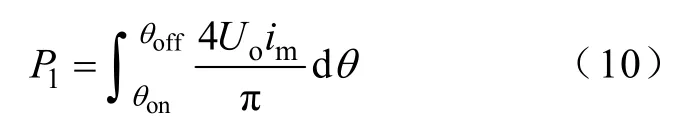
将 3.1 中求取的发电电流解析式分段带入式（10）即可得到在励磁区间主绕组的输出功率。为简化分析，作如下假设：

（1）励磁绕组电流上升时间很短，认为θon≈θ1。

（2）转速ω足够大，满足Kmω＞＞R。

（3）波形系数K受开通、关断角影响较小，近似为常数。

基于上述假设，输出功率P1可以表示为

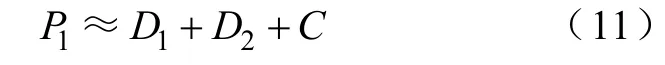
式中，C为与励磁角度无关的常量；D1、D2表达式如下：

由于励磁区间宽度恒为15°，θon、θoff、θm满足下面关系式

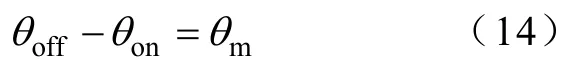
当θon+Lmmin/Km=-θoff+Lmmin/Km+2θm时，D1、D2取极小值。相对应的开通、关断角为

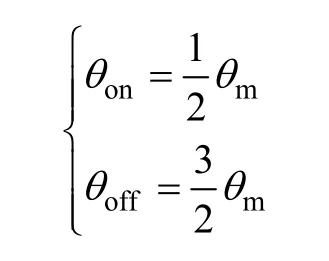
此时在励磁区间主绕组输出功率为极小值。当开通角θon∈[0，θm/2]时，P1为θon的减函数；θon∈[θm/2，2θm]时，P1为θon的增函数。

3.3 续流区间输出功率分析

在续流区间[θoff，θ4]内，悬浮绕组关断，主绕组续流发电。与普通开关磁阻发电机原理类似，励磁结束时对应发电绕组电流iD（见图2）是衡量发电机在续流区间输出功率的重要指标。iD越大，输出功率越高。

根据发电电流解析式，可以解出主绕组电流由负变正的角度θ0。图4 为关断角θoff＜θ0、θoff=θ0、θoff＞θ0时对应的电流波形。

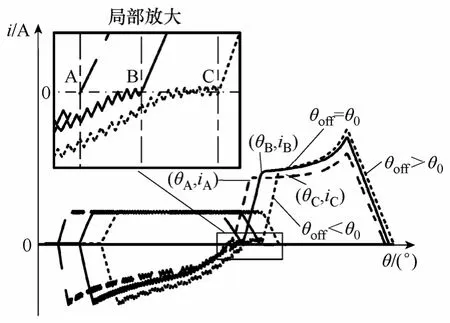
图4 三种情况下对应发电电流波形Fig.4 Generating-currents waveforms unde three conditions

励磁电流为零时对应的发电电流iD大小分别为iA、iB、iC。

以虚线电流为零时的A 为原点，联立绕组电压方程（1）和（2），得到θoff＜θ0时励磁电流、发电电流在区间[θ0，θ2]的解析式

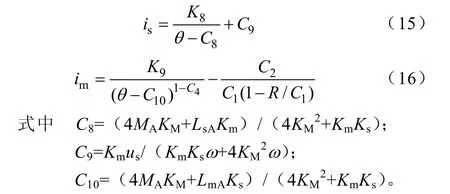
MA、LmA、LsA为A 处绕组互感、主绕组自感和悬浮绕组自感。isA为A 点对应的励磁电流，将点（isA，0）带入式（15），得到波形系数K8=C8（C9-isA）。将点A（0，0）带入式（16），得到

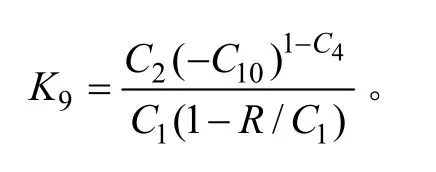
令式（15）中is=0，即可求得励磁电流为零时的角度θA=isAC8/C9。

将（θA，iA）代入式（16），求得iA的解析式

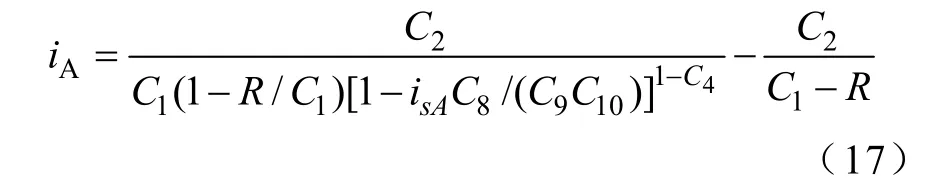
同理，分别以B、C 为原点，可得iB、iC的解析式

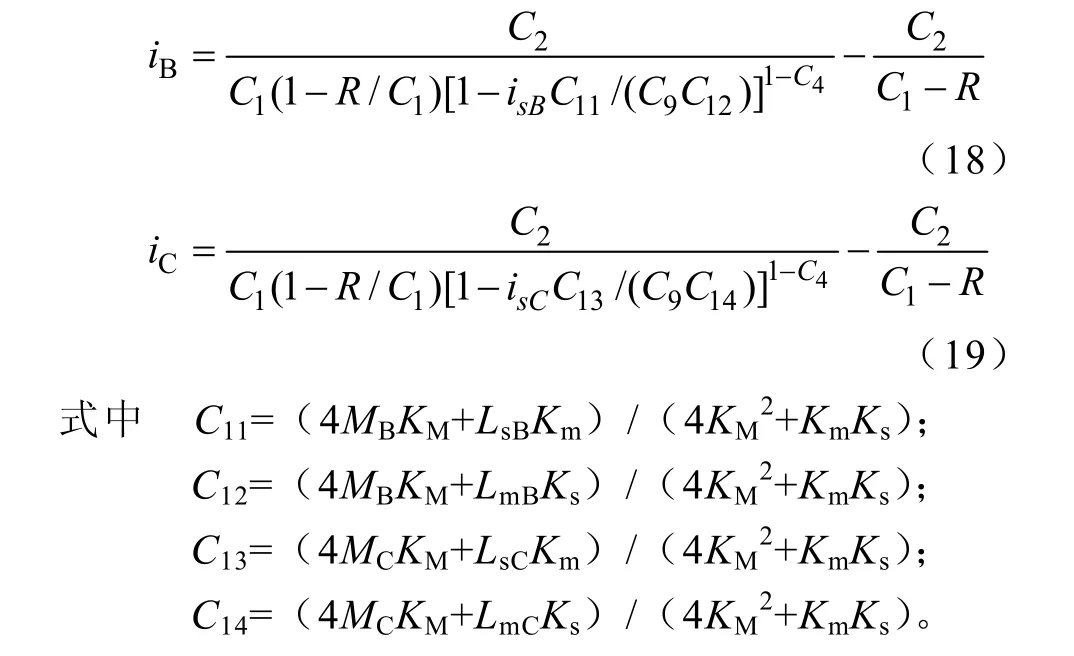
式中，MB、LmB、LsB、MC、LmC、LsC为分别在B 点和C 点处绕组互感、主绕组自感和悬浮绕组自感；isB、isC为B 点和C 点对应励磁电流大小。

根据关断角和θ0的关系，isA、isB、isC与励磁电 流给定值满足以下关系式

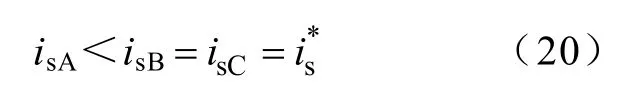
对于同一台电机，满足C8/C10=C11/C12=C13/C14。将其带入式（17）～式（19），得到

当θoff＜θ0时，励磁绕组关断角对应的发电电流为负值。因此，相对于θoff=θ0的情况，励磁电流降为零时，主绕组电流iA＜iB。所以，在续流阶段，θoff=θ0时发电机输出功率大于θoff＜θ0时的输出功率。

当θoff＞θ0时，发电电流在区间[θ0，θoff]内由负变正，电流换向引起整流桥换臂，电压方程（2）中绕组电压Uo变为-Uo。发电绕组在反压作用下上升斜率受到抑制，发电电流出现了凹陷。因此，尽管iC=iB，θoff＞θ0时发电机在续流阶段输出功率仍小于θoff=θ0时的输出功率。

综上所述，在续流阶段，关断角正对θ0时，发电机输出功率最大。

3.4 总输出功率分析及优化

无轴承开关磁阻全周期发电机在整个周期内的输出功率P为励磁区间输出功率P1与续流区间输出功率P2之和。

定义电机定、转子齿极对齐位置为0°。根据3.2 节的结论，关断角θoff=θ0时，P2达到最大值。此时θon=θoff-15°，即可确定一组优化的开通、关断角，但励磁区间输出功率也因此确定，不能进行优化。为综合考虑励磁区间和续流区间的输出功率，根据试验样机参数，在Matlab/Simulink 中搭建了电机仿真模型，进行输出功率的仿真验证。

仿真参数为转速n=3 000r/min，励磁电流给定 值=3A，励磁电压Us=20V，负载电阻R=5Ω，未 加悬浮力。在此条件下计算出θ0≈7.5°。图5 为开通角从-13°变化到-3°时对应电机的输出功率。

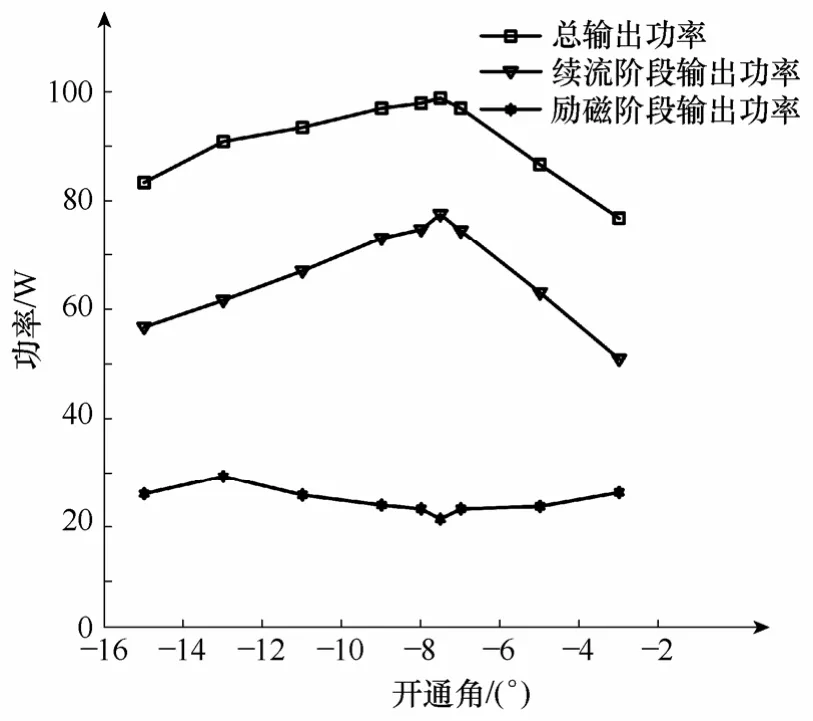
图5 不同励磁开通角时的电机输出功率Fig.5 Output power under different turn-on angles

图5 中仿真结果与3.2 和3.3的理论分析结果相吻合。θon=-7.5°，θoff=7.5°时，励磁阶段输出功率P1取极小值。由于θ0=7.5°，关断角θoff=θ0，续流阶段输出功率P2处于极大值。相对于P2，P1受开通角影响较小，因此，总输出功率在θon=-7.5°时取最大值。

根据仿真结果，励磁阶段输出功率对总输出功率影响相对较小。因此，无轴承开关磁阻全周期发电机输出功率优化主要是针对续流阶段输出功率的优化。其励磁区间选取流程图如图6 所示。试验样机的参数下θ0≈7.5°，最优的励磁区间为[-7.5°，7.5°]，不同电机参数对应的θ0不同，可以根据3.1 中电流解析式计算得到。

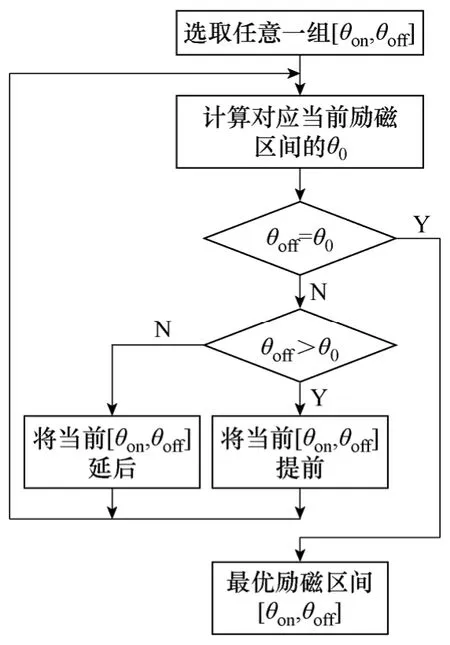
图6 最优励磁区间选取流程图Fig.6 Flow chart of selecting optimal excitation period

3.5 悬浮力对输出功率的影响

上述分析都是针对发电机未加悬浮力时的情况。考虑悬浮力时，发电绕组电压方程为

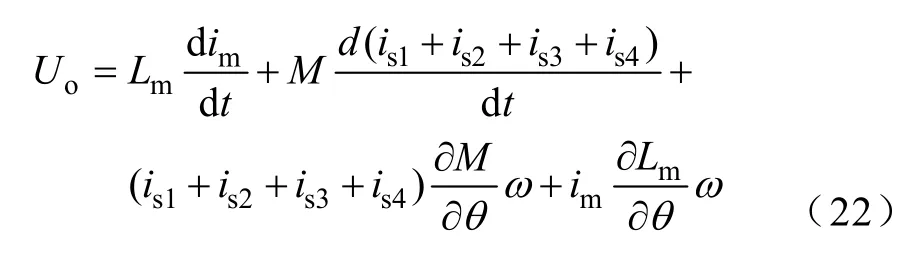
式中，is1、is2、is2、is4为当前导通相悬浮绕组电流。根据文献[17]中悬浮力的控制策略，悬浮绕组一相4 极电流满足=（is1+is3）/2=（is2+is4）/2。式（22）可转化为

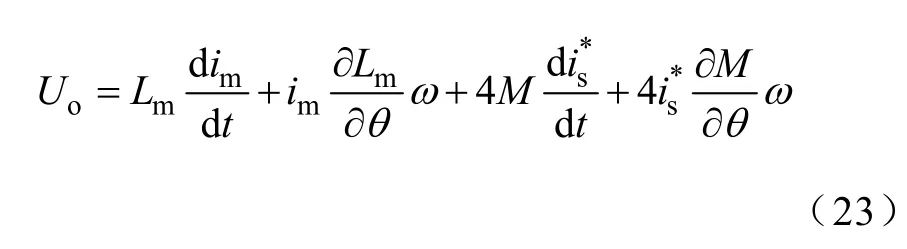
此时，绕组电压方程与不考虑悬浮力的情况相同。因此，悬浮力对发电机输出功率并无影响。

图7 为悬浮力对发电机的影响图，实线为α、β方向施加5N 悬浮力后发电电流仿真波形。可以看出，实线与虚线基本重合，即悬浮力施加前后的电流包络面积基本相等，可认为两种情况下的输出功率相等。因此，未考虑悬浮力时输出功率的优化策略对考虑悬浮力的情况同样适用。

4 实验结果

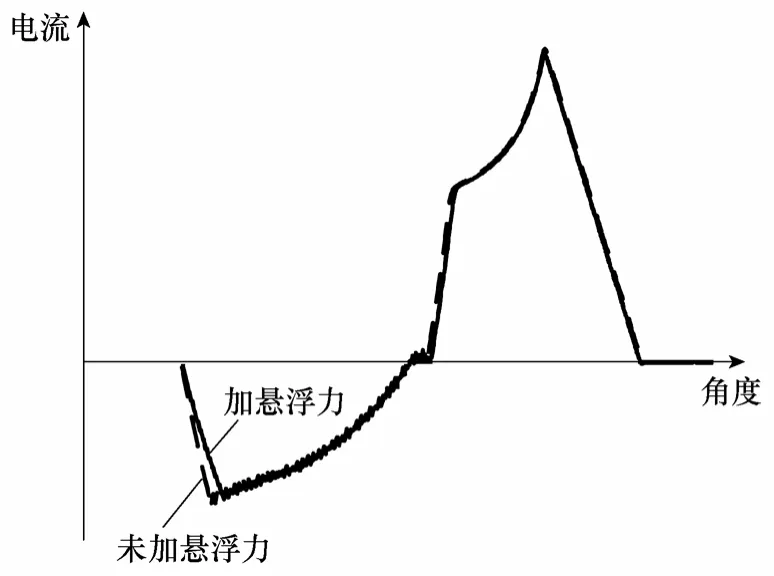
图7 悬浮力对发电电流影响Fig.7 Influence of levitation forces on generating-current

实验样机参数为:电机为12/8 结构，主绕组和悬浮绕组分别为17 匝和60 匝，定、转子极弧度数 为15°，定子轴向长度为55mm，轭部直径为110mm，铁心外径 123mm，铁心内径 54mm。转子极半径26.75mm，轭部直径35.5mm；转轴直径17mm；平均径向气隙长度0.25mm。额定功率1kW，主绕组额定电压50V，励磁绕组额定电压100V，额定转速8 000r/min；最大径向负载50N。图8 为无轴承开关磁阻全周期发电机实验平台，发电机由高速异步电动机拖动，高速异步电机通过高速变频器驱动。实验样机如图8b 所示，其左端为悬浮端，如图8c 所示。辅助轴承采用深沟球轴承，轴承与轴的间隙单边为0.2mm。4 个电涡流位移传感器分别固定在悬浮端±α、±β四个方向，通过实时检测转轴位置实现位移闭环控制。右端是非悬浮端，轴承采用调心轴承，通过波纹管联轴器与轴承座相连。

图8 全周期发电实验平台Fig.8 Picture of experimental platform

图9 为转速5 200r/min 时的发电绕组相电压和 电流实验波形。励磁电流给定值=3A，励磁电压Us=20V，负载电阻R=5Ω。其中，Q5为功率管开关信号，uo为发电绕组电压，is为悬浮绕组励磁电流，im为发电绕组电流。

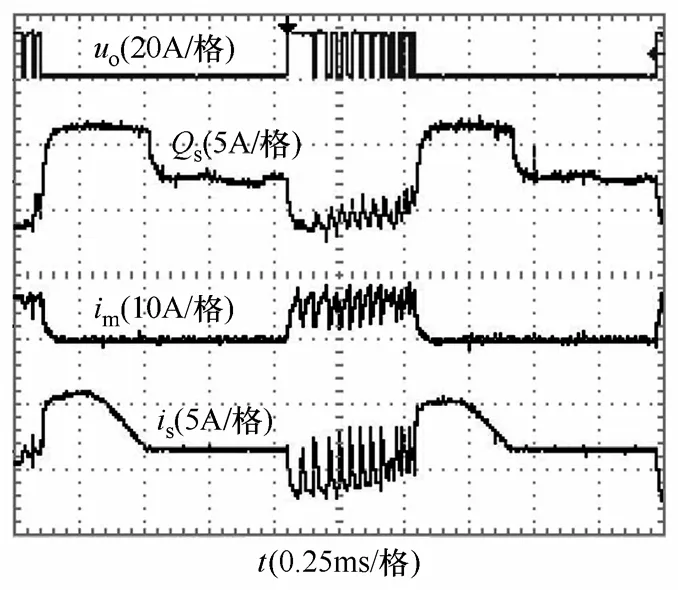
图9 样机电流波形Fig.9 Experimental current waveforms

图10 为在不同励磁区间和转速下，发电机输出功率曲线。随着转速升高，输出功率增大。当励磁区间从[-15°，0°]变为[-7.5°，7.5°]的过程中，输出功率升高，而当励磁区间进一步推迟以后，输出功率下降。所以[-7.5°，7.5°]可作为最优励磁区间。在转速n=3 000r/min 时，仿真结果与实验结果数值相近，但输出功率随励磁区间变化略微偏小，这是由于仿真模型未考虑相间互感。图11 为在不同励磁区间和转速下，发电机效率曲线。图12 为励磁区间[-7.5°，7.5°]，转速n=3 000r/min 时稳态悬浮位移、电流波形。转轴在α和β方向的位移，悬浮位移控制在125μm 左右，两者均小于转轴与轴承内圈的单边位移。从实验现象看，转轴在高速旋转时，轴承内圈静止不动，这表明转轴已脱离轴承的支撑，实现悬浮发电运行。实验结果表明了本文提出的优化理论的可行性。

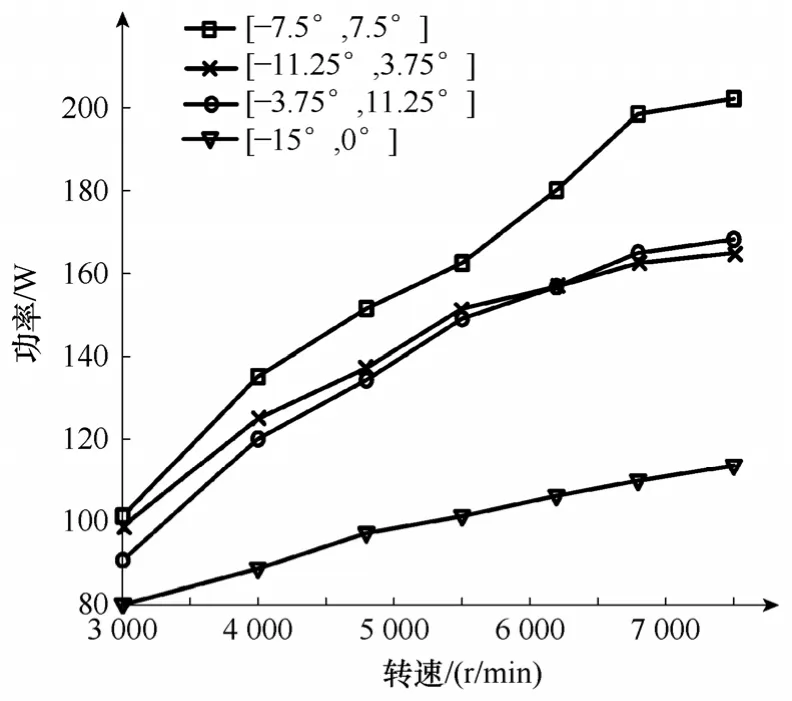
图10 不同励磁条件下输出功率曲线Fig.10 Output power curves under different excitation conditions

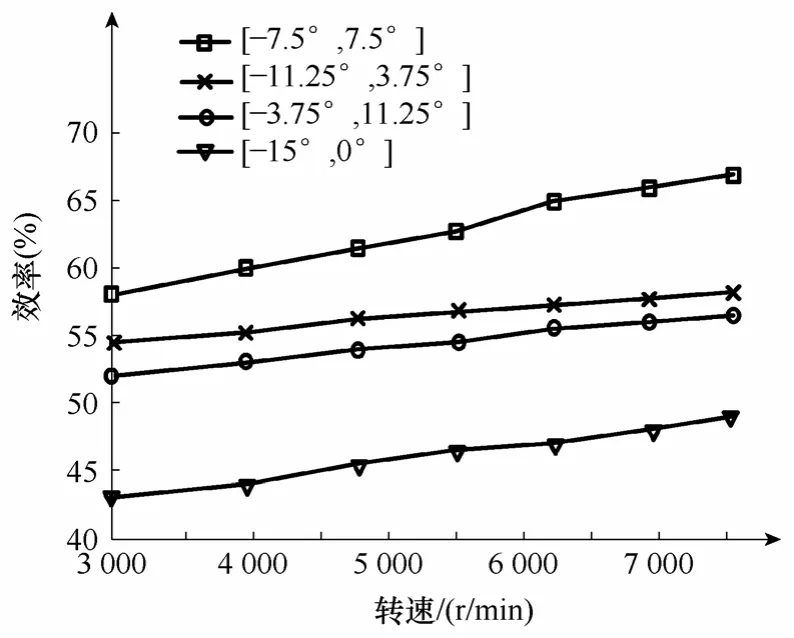
图11 不同励磁条件下效率曲线Fig.10 Efficiency curves under different excitation conditions

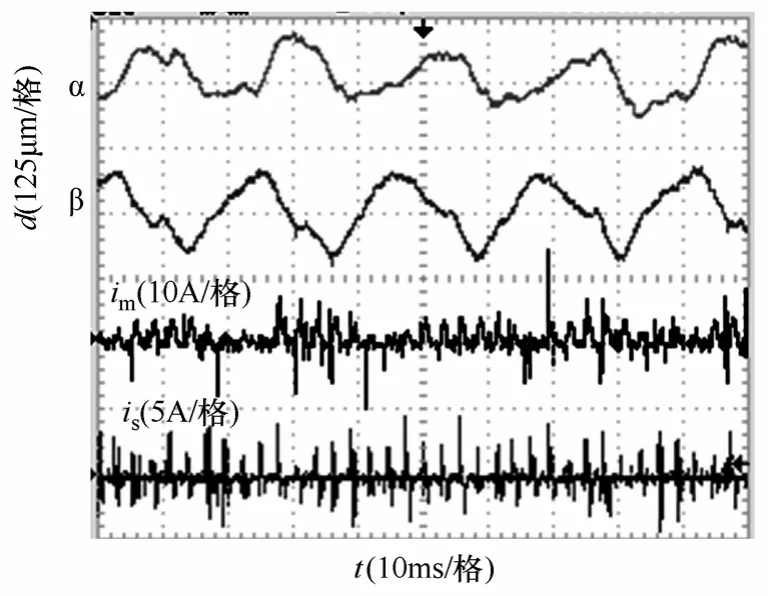
图12 样机在n=3 000r/min 时的试验波形Fig.12 Experimental waveforms at a speed of 3 000r/min

5 结论

本文针对 12/8 极的无轴承开关磁阻全周期发电机，根据绕组电压方程分段推导了相电流解析式，在此基础上研究了输出功率的优化控制。

（1）基于励磁阶段输出功率的解析式，分析了励磁开通、关断角对励磁阶段输出功率的影响。

（2）分析了励磁关断角对续流阶段输出功率的影响。通过优化关断角，使续流阶段输出功率最大化。

（3）研究了悬浮力的影响。通过理论和仿真验证了悬浮力对发电机输出功率没有影响。

（4）提出了对应试验样机的最优励磁区间，最后通过实验验证。

[1]詹琼华,开关磁阻电动机[M].武汉：华中理工大学出版社,1992．

[2]吴建华.开关磁阻电机设计与应用[M].北京:机械工业出版社,2000.

[3]Takemoto M,Shimada K,Chiba A,et al．A design and characteristics of switched reluctance type bearingless motors[C]．4th International Symposium on Magnetic Suspension Technology,1998:49-63.

[4]Takemoto M,Suzuki H,Chiba A,et al.Improved analysis of a bearingless switched reluctance motor[J].IEEE Transactions on Industry Applications,2001,37(1):26-34.

[5]Takemoto M,Chiba A,Akagi H,et al.Radial force and torque of a bearingless switched reluctance motor operating in a region of magnetic saturation[J].IEEE Transactions on Industry Applications,2004,40(1):103-112.

[6]邓智泉,杨钢,张媛,等.一种新型的无轴承开关磁阻电机数学模型[J].中国电机工程学报,2005,25(9):139-146.Deng Zhiquan,Yang Gang,Zhang Yuan,et al.An innovative mathematical model for a bearingless switched reluctance motor[J].Proceedings of the CSEE,2005,25(9):139-146.

[7]杨钢,邓智泉,张媛,等.无轴承开关磁阻电机实验平台的设计与实现[J].中国电机工程学报,2006,26(22):97-103.Yang Gang,Deng Zhiquan,Zhang Yuan,et al.The design and realization of experiment platform of a bearingless switched reluctance motor[J].Proceedings of the CSEE,2006,26(22):97-103.

[8]曹鑫,邓智泉,杨钢,等.新型无轴承开关磁阻电机双相导通数学模型[J].电工技术学报,2006,21(4):50-56.Cao Xin,Deng Zhiquan,Yang Gang,et al.Novel mathematical model of bearingless switched reluctance motors with two-phase excitation[J].Transactions of China Electrotechnical Society,2006,21(4):50-56.

[9]邓智泉,张宏荃,王晓琳,等.无轴承异步电机悬浮子系统独立控制的研究[J].中国电机工程学报,2003,23(9):107-111.Deng Zhiquan,Zhang Hongquan,Wang Xiaolin,et al.Study on independent control of the levitation subsystem of bearingless induction motors[J].Proceedings of the CSEE,2003,23(9):107-111.

[10]仇志坚,邓智泉,王晓琳.无轴承永磁同步电动机的独立控制研究[J].中国电机工程学报,2006,26(1):115-119.Qiu Zhijian,Deng Zhiquan,Wang Xiaolin.A study on independent control of the bearingless permanent magnet synchronous motor[J].Proceedings of the CSEE,2006,26(1)：115-119.

[11]王宝国,王凤翔.磁悬浮无轴承电机悬浮力绕组励磁及控制方式分析[J].中国电机工程学报,2002,22(5):105-108.Wang Baoguo,Wang Fengxiang.Excitation and control analysis of levitation force winding for magnetic suspension bearingless motor[J].Proceeding of the CSEE,2002,22(5):105-108.

[12]孙玉珅,吴建兵,项倩雯.基于有限元法的磁悬浮开关磁阻电机数学模型.中国电机工程学报,2007,27(12):33-40.Sun Yukun,Wu jianbing,Xiang Qianwen.The mathematicmodel of bearingless switched reluctance motor based on the finite-element analysis[J].Procee-dings of the CSEE,2007,27(12):33-40.

[13]Clin F,Yang S M.Self-bearing control of a switched reluctance motor using sinusoidal currents[J].IEEE Transactions on Power Electronics,2007,22(6):2518-2526.

[14]Chen L,Hofman W.Analytically computing winding currents to generate torque and levitation force of a new bearingless switched reluctance motor[C].12th International Power Electronics and Motion Control Conference,Portoroz Slovenia,2006：1058-1063.

[15]曹鑫.无轴承开关磁阻发电系统的基础研究[D].南京:南京航空航天,2003.

[16]Cao Xin,Deng Zhiquan.A full-period generating mode for bearingless switched reluctance generators[J].IEEE Transactions on Applied Superconducti-vity,2010,20(3):1072-1076.

[17]刘泽远,邓智泉,曹鑫,等.全周期无轴承开关磁阻发电机的设计[J].中国电机工程学报,已录用.Liu Zeyuan,Deng Zhiquan,Cao Xin,et al.Design of a full-period bearingless switched reluctance generator[J].Proceedings of the CSEE,2010,Accept.

[18]曹鑫.12/8 极无轴承开关磁阻电机[D].南京:南京航空航天大学,2011.

附 录