带有单向离合器的蛇形带传动的分段线性动力学分析

1 前言

蛇形带是汽车的前端辅助功率传动（FEADS），是一个简单的带把功率由曲轴传递到多种附件。已经由一系列的研究［1－9］分析该装置的线性和非线性结构。在参考文献［1］到［3］中介给了一种集中考虑带轮扭转振动的弹簧类带模型。在文献［4］到［7］中，对于蛇形带采用绳索类带传动体原理研究带的横向振动和带轮的扭转振动。Beikmann等［5］开发了一三带轮系统的样机，它包含一主动带轮和一从动带轮以及一张紧轮（图1）。该张紧轮由一绕其支点回转的刚性臂和销连接在臂另一端的带轮组成，它保持工作时带的张紧。

采用该标准的三带轮装置，Kong和parker［8］考虑了带的弯曲刚度建立了一个复合的连续一离散模型。求得了许多稳态均衡解决方法。和绳索类带传动不同，非明显跨距均衡曲率产生，它引起带横向振动和扭转振动的组合振动。在其后续的研究［9］中，通过不具有绳模型的系统模态分析研究跨接带轮连接，该连接由实验检测［6］。

在机械系统如喷气发动机［10］的气体涡轮机的起动装置直升飞机的主转子和某些带轮以及FEADS［11－15］中采用单向离合器，当从动件或功率吸收组件（即一自动辅助装置）超越主动件（即带轮）时离合器脱离。对比中，当它们的速度相同时，该两组件是彼此锁紧或通过弹簧类元件连接。接合可确保传递功率，而脱开时，两个不连接的组件超越时，可降低或避免从动件的重大影响。该影响诸如包括系统振动，带的拍动，带磨损和由带一带轮摩擦产生的吱叫声。本文则考虑将单向离合器用于蛇形带传动中。

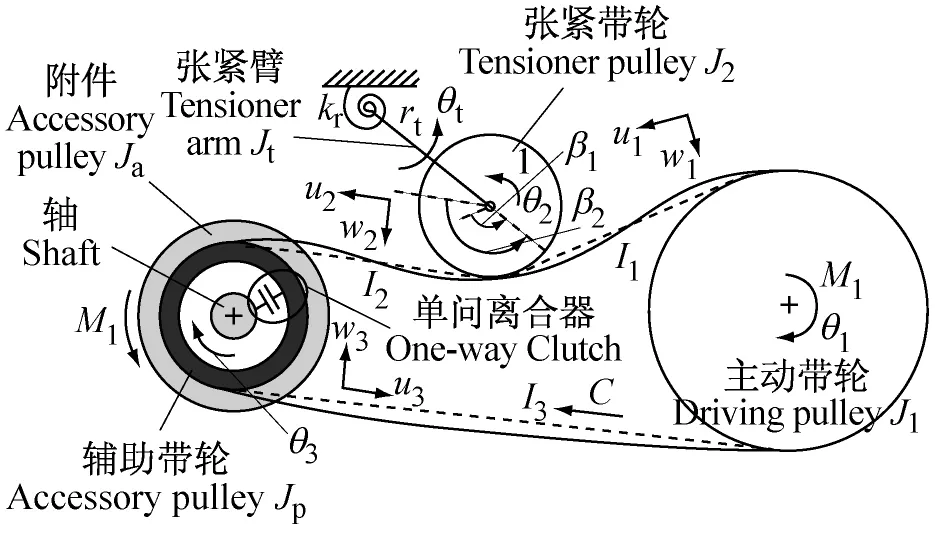
图1 集合从动带轮和其结合附件的具有单向离合器的三带轮装置为简化起见已省略了物理量Fig.1 Three－pulley system with a one－way clutch integrated in the driven pulley and its associated accessory.The tildes on the physical quantities have been for simplicity

Vernay等［10］实验研究楔形单向离合器的瞬态特性，证明了离合器啮合时滑动的影响。Solfrank和Kelm［12］制订出一辅助传动装置运行的全面模拟方法。该单向离合器的模型由一速度相关减振和转矩由带轮传至辅助部件具有非线性刚度的一并联弹簧组成。只有当辅助件速度低于带轮速度时离合器才介入作用。Leamy和 Wasfy［15］开发了一动力学有限元模型确定带轮一带传动装置的瞬态和稳态响应。为证明该方法的实用性，采用结合装置的从动带轮中一比例转矩法则模拟一单向离合器。并仿真其瞬态响应。

但以上所述著作均未涉及详述单向离合器的动力学，zhu和 parker［13，16］的具有单向离合器和从 动带轮及其辅助件组合的一双带轮一带装置模型检测其非线性动力学，该离合器是一采用间断刚度的分段非线弹簧，它仅在其连接部件正相对位移时啮合，通过交替啮合和脱开特性的仿真，证实了它是一典型适度的非线性特征。离合器分开带轮和辅助件后成为二个自由度（DoFs），而其功能像一个减振器降低振动。Mockensturm和Balaji［14］提出一分段线性分析法研究单向离合器的动特性，其模拟是基于带轮和辅助轴的相对速度。离合器运行导致传递功率增加和带牵引力波动减少。

在上述研究中，仅考虑了带的扭转振动。为对具有单向离合器蛇形带传动的动力学更合乎实际的检测，本文采用了典型的三带轮系统［图1］，以及采用混合连接一离散模型见参考文献［8］和［9］，其中组合了带的弯曲刚度和展示带一带轮连接。从动带轮和其辅助件之间的组合，当两组件脱开和啮合运动时，单向离合器分别分离和锁紧。对于这个分段线性系统，在各线性结构中，通过转换矩阵［17］在不连续的时间序列内估算分析解。采用两个临界值求出瞬态转变时间，即零相对速度和零离合器转矩。该解用数值积分证实。对已知的设计装置，通过激励频率范围，带轮和辅助件的惯量比以及外载荷研究单向离合器在该系统动态冲击。检验带的动态拉力的降低。

2 传动装置的模拟

图1示典型的三带轮一带传动装置。带以常速度c运行，把功率由主动带轮传到从动（辅助件）带轮。张紧器臂是钢丝弹簧以弹簧刚度kr加载，一激励转矩作用于主动带轮，而辅助件承受一固定外转矩。

与相对速度有关的单向离合器是设置于从动带轮和由带驱动传递功率的辅助件之间，该离合器模型应用于楔块型，滚子型或缠绕弹簧型单向离合器。首先考虑离合器脱开，带轮速度低于辅助件速度，当相对速度接近零时，带轮和辅助件彼此锁紧，即离合器啮合。啮合时，带轮和辅助件彼此被离合器内转矩制约运动。在这种情况，带轮惯量Jp和辅助惯量Ja组合成一刚体惯量Ja＝Ja＋Jp。当离合器转矩由正值降到零时，带轮和辅助件脱开。离合器啮合和脱开状况的数学表达式和其转换法则列于表1。这是两啮合和脱开结构的分段线性系统线性工作状况。

Kong和parker［8］采用Hamilton原则导出了三带轮一带装置非线性运动方程式，这里带模拟为一运动的弯曲樑，三带轮的始点和终端的跨距与直带相同。所含有的有限带的弯曲刚度造成非一般的稳态跨距曲率，确定带和带轮之间联接程度工作状况，在绳形带模型内基于直线段稳态曲率对比带一带轮分离运动，再线性化方程式约非一般均衡并在自由振动分析［9］方面研究带一带轮联接。

在本装置中，线性化啮合形式无因次操纵方程式与这些参考文献［9］相同，并写成广义算式为

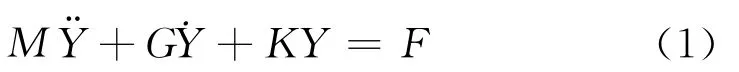
式中Y＝｛y1，y2，y3，θ1，θ2，θ3，θτ｝T集合带连续和离散间隔以及带轮和张紧器转化为扩散可变，θi和θt概括带轮和张紧器臂转角，它们近于相等。θ3为啮合时辅助件一带轮的转角，即θ3＝θp。θa为假如一个循环发生脱开时，包括刚体运动辅助件的转角，yi为各间隔wi有关的横向位移，如

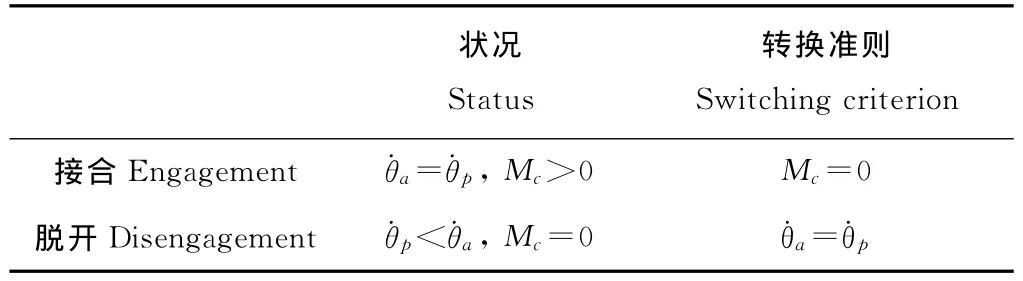
表1 离合器接合和脱开状况及其转换准则Table 1 Engagement and disengagement statuses of the clutch and their switching criteria

式中x1，2∈［0，1］沿各间隔空间可变，rt为张紧器臂长度，li为间隔长度。yi满足普通的边界条件如锁紧梁。微分运算子M和K 是自伴，而G是不对称自伴，具有一个合适的内部结果确定于参考文献［9］。F是附件负荷组成的矢量，如

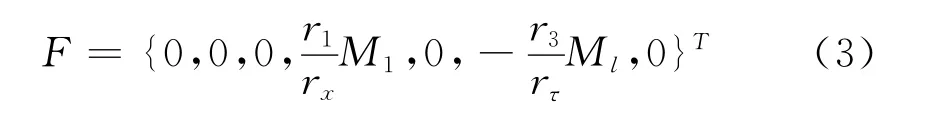
以下为参考文献［9］中无因次数，该无因次量为

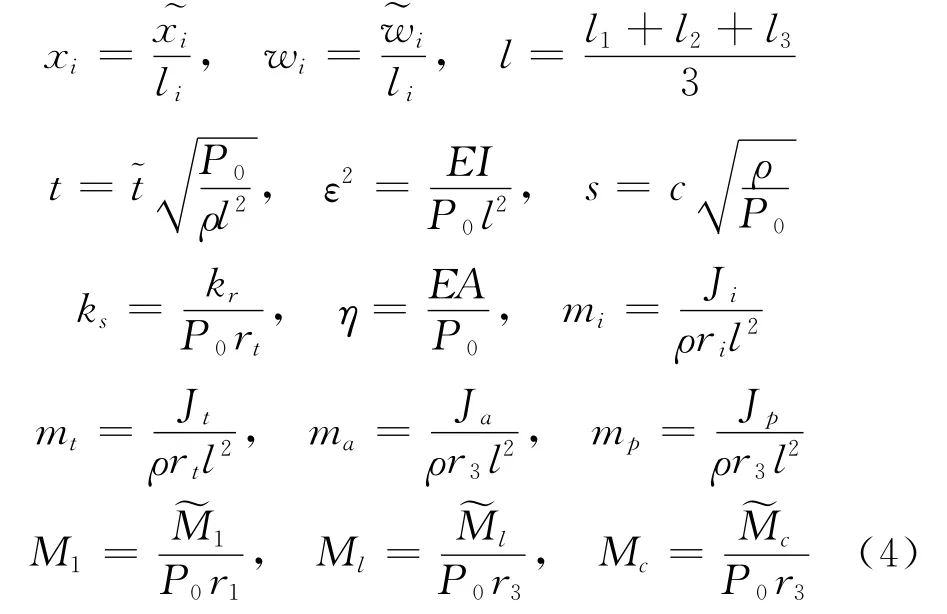
式中“～”符号指为物理量，对离合器啮合状况m3＝m0，考虑附件作为与带轮分开的自由刚体，其运动方程为

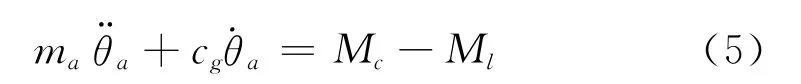
式中Mc＞0为强制啮合，Cg为附件阻尼。

公式（1）还用于离合器脱开状态，但仅带轮惯量是有效的，即m3＝mp。在这种情况下，θ3在式（1）内只表示为附件一带轮的转角，即θ3＝θp和F＝0。附件由带轮和转臂分开转动负荷独立，满足式（5）但具有零离合器转矩Mc＝0。

［9］相同，Galerkin离散化用于混合离散一连续系统（1）。扩展变数γ展开为系列基础函数为

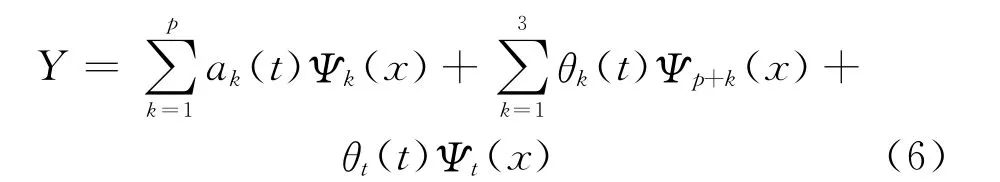
式中p＝N1＋N2＋N3和Ni为第i跨距的各个基础函数。Ψi是满足所有边界条件的全面比较函数，而其中的每个函数都描述整个系统的一个变形。对于第i间隔，间距变形的形状为正弦曲线Sin（kπx），k＝1，…，Ni的迭加。对于瞬时，Ψk＝｛kπx，0，0，0，0，0，0｝T，对于第1间隔K＝1，…，N，对于离散的带轮和张紧的臂，该完整的比较函数只包含有关的离散单元，如对于带轮2，如对于带轮2Ψp＋2＝｛0，0，0，0，1，0，0｝。在参考文献［9］采用内积确定离散方程：

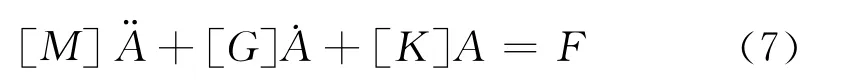
式中 A（t）＝｛a1（t），…，ap（t）θ1θ2θ3θτ｝T为一般化座标。

在车辆中，发动机气缸点火和压缩冲程的交替变化，造成曲轴速度的循环波动。基于发动机特性一特定的周期速度不规则，对于这样特定的曲轴速度，省去加于主动带轮上转矩M1，而在所有期间，式（7）中作为激励移到左边，结果为

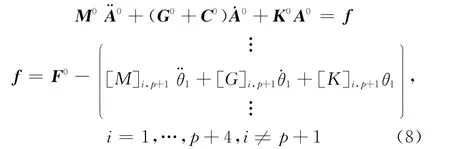
式中上角的0表示由原点第（p＋1）行和所消去导出的新矩阵和矢量。C0是由典型阻尼收集在跨距和轴承的能量损耗求得的阻尼矩阵，式（8）和（5）联立和表1中的转换准则充分描述了系统的运动动力学。

3 方法

另一种离合器啮合或分离状态可由线性系统理论得出，分离（8）式求得一状态空间变量并转换（8）为

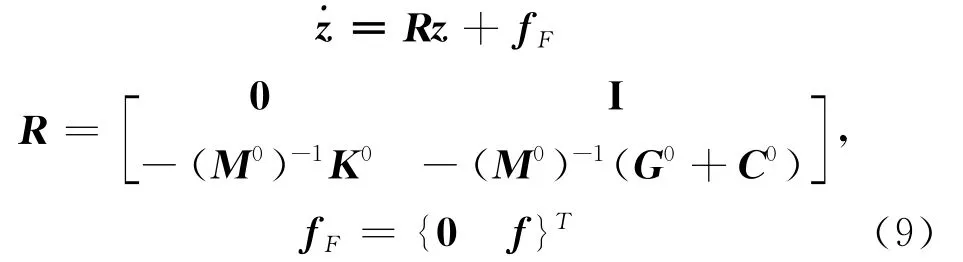
式中Ⅱ为－（p＋3）×（p＋3）恒等矩阵，此外，一求得的模态R的矩阵V和导出的模态座标矢量q为

将式（10）代入式（9），左边乘以 V－1，得离散方程

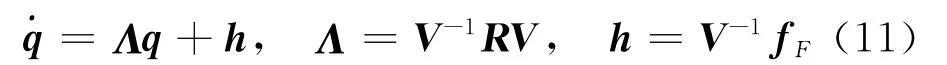
式中Λ是斜线符号，方程式（11）的解为

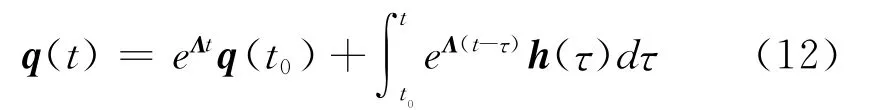
其中τ0为起初时间，eΛ（t－τ）为转换矩阵。

其一可在式（12）内积分数值估算，然而在任何瞬时t转换矩阵已由t0到t求积估算。对于数值化效率，其一可在各个瞬时t∈［t0，t5］存储转移矩阵避免重复矩阵估算，其中tf为最后的时间。这种对系统相当好的工作具有少量DoFs和少量积分时间点。对于该系统和实际之一有较多的跨距和带轮，该离散系统要求有许多DoFs和许多波动循环确保瞬态响应完全延迟取得稳定状态。因此，式（12）数值估算无效。

Meirovitch［17］提出一个分析近似方法，在离散时间序列内，对于tk＝t0＋kΔt估算在t0，…，tk，…，tN的解，其中 N＝（tf－t0）／Δt，该近似法采用在这里为

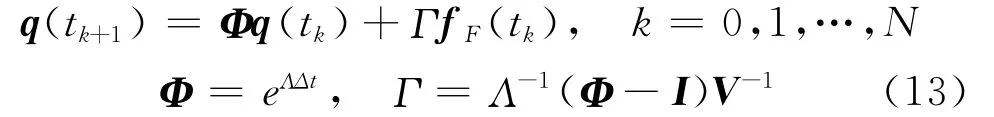
式中Δt为取样时间选择足够小，如输入矢量fF（t）可考虑作为大于时间间隔tk＜t＜tk＋1的常数。用式（10）引起的物理响应，由数值积分确认该解，当与数值积分比较时，该方法要求的计算时间为它的30－50%。

对于离合器工作不同变换必定要求有瞬时的过渡时间，当它接合时，应监测离合器转矩。在各个瞬时，用由式（13）和（10）求得响应。该附件响应˙θa和是已知的，因为附件随带轮相互运动。因此，离合器转矩可由式（5）确定。如果Mc＝0（或小于数值补充内的特定的公差），从下一瞬时开始脱离。对比离合器虽然脱离，相对速度是受到控制的。由式（13）和（10）求得，由式（13）和 Mc＝0求得结果，如果（在特定公差之内），离合器回复接合。

上述方不限制离合器在一个单循环内接合和脱开之间的交换，不似参考文献内的分析解，其中仅假定一单次转换。

4 结果和讨论

由于曲轴速度波动系统受到激励的稳态周期响应考虑为˙θ1＝DcosΩt，该激励频率Ω是发动机（曲轴）速度的σ倍。其中σ由发动机缸数确定，本研究采用σ＝3。带速度随发动机速度改变为s＝r1Ω／（σl）。范围Ω＝0－12相应为发动机速度对在表2内参量变化在0－5850转／分以上，它是一个实际主要的频率范围。该带速对应于Ω＝12为s＝0.921低于任何临界速度，它是陀螺仪非稳定工作造成的。曲轴速度波动振幅D独特按发动机速度百分比μ估算的，因此D＝μΩ／σ。虽然发动机速度取决于实际，但这里选定μ＝10%。

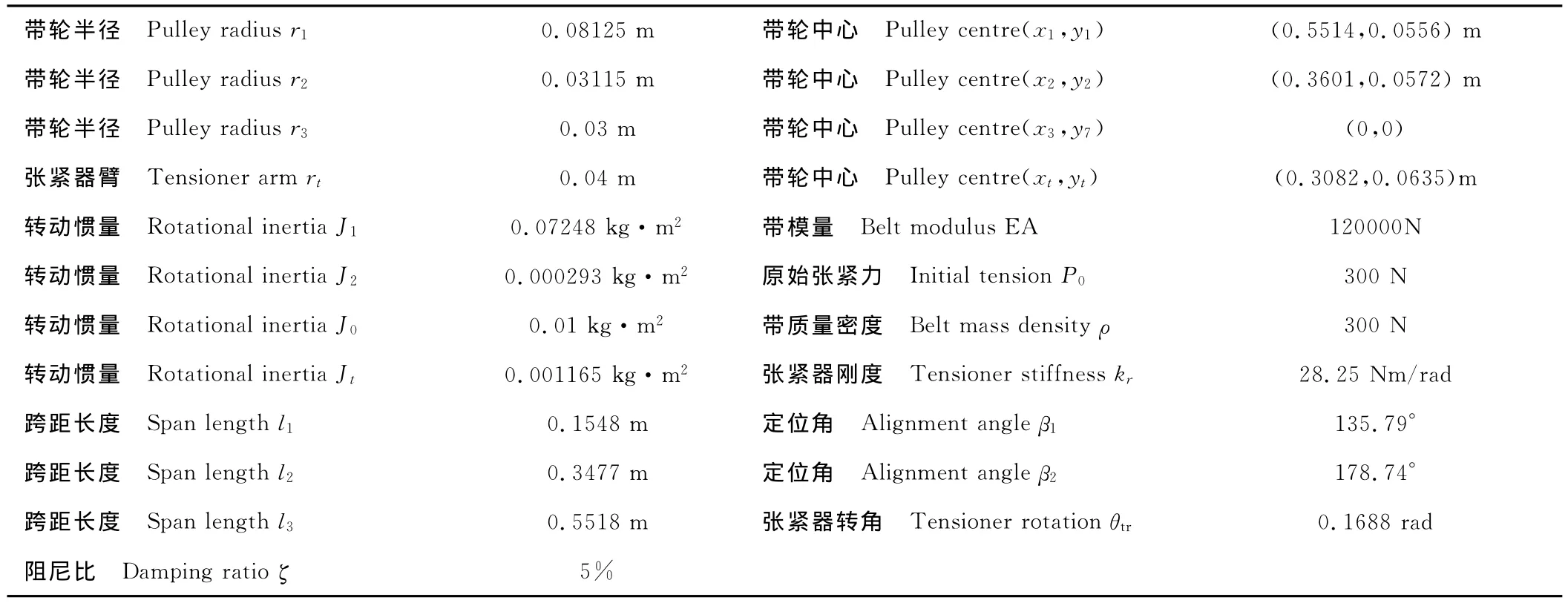
表2 实例系统的物理特性Table 2 Physical properties of the example system

该参量α是附件和从动带轮的惯性比，即ma＝αmb。本文始终认为带轮和附件的组合惯量不变，对于任何α作为m0＝26.03（J0＝0.01kgm2）。对于离散化，对于i＝1，2，3即半正弦或正弦曲线考虑选择Ni＝2。在式（8）内ζ＝5%和附件阻尼Cg＝0.2求得模态阻尼系数C0。

激励频率Ω为变数，带速和线性系统的固有解改变［9］。对于小的弯曲刚度，横向强制振动的自然频率随速度增加而迅速减小，而扭转强制振动的自然频率却变化少许。对于大的弯曲刚度，因为带一带轮联接紧密，故所有自然频率均随速度比较慢和非单调地减少。本文采用中等的弯曲刚度ε＝0.02，由这些中等数值，用不同弯曲刚度进行模拟，进一步确认大多数结果是不变的。

为了比较两具有单向离合器的两非线性系统，研究两线性系统。一个系统相应为离合器持久啮合状况，称为“锁止”离合器装置。它在实际装置中表明为一没有离合的标准的布置，带轮与附件刚性联接。在这种情况下，m3＝m0。其他情况参照这个情况，当离合器安全脱开，带仅由带轮的惯量m3＝mp＝m0／（1＋α）驱动，这种称为不接合离合器装置。

实际从动轮的惯量是依据组合惯量（当离合器锁止时）到带轮惯量（当离合器脱开时）变化，而自然频率也相应改变。图2示导致带速s＝0.069（Ω＝0.9）表明这种变量，其中α＝0相应锁止离合器装置的自然频率。对于表2中的参量，扭转强制振动对于两线性系统有一个最小的自然频率。按照图2，开始随α很快增加，但对于大的α进一步Ω1增加并不明显，而张紧器臂最后受这种方式控制，α不再影响Ω2，形式由跨臂横向振动控制。根据α＝0的一个x指出附件一带轮一控制方式的自然频率随α单调增加，例如当α＝0时Ω＝2.7。反之，对于α＝10，Ω＝4.7和α＝50，Ω＝9.2。当这种模式的自然频率接近另一自然频率时，自然频率发生。例如，它接近Ω3，Ω4，Ω5和Ω6时，则分别α＝2.7，8.3，21和26附近（图2中破折线图所示）。在转向区之外，该模态特征除其自然频率变化外，形式保持相同。对于大的α，其他形式的能量分布和其有关联的自然频率接近稳定状态。对于大的α，具有Ω3－Ω6的形式用横向振动控制。图2给出了各个自然频率的极限值，当带速（激励频率）改变时，这些自然频率少许变化。

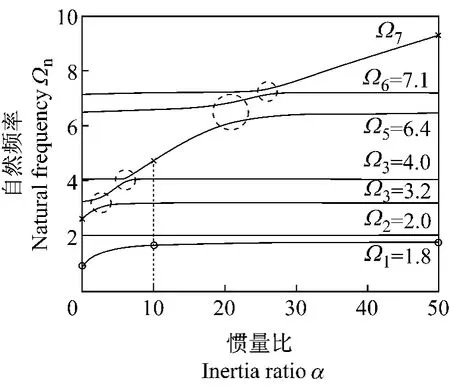
图2 对于带速s＝0.69（Ω＝0.9）和其他参量列于表2脱开离合器装置的自然频率随惯量比α变化，破折线圆表示为自然频率转向区Fig.2 Natual frequencies of the disengaged clutch system varying with inertia ratioαfor belt speed s＝0.69（Ω＝0.9）and other parameters in Table 2.Dashed circles indicate regions of natural frequency veering

4.1 激励频率段

图3示三跨距（a1，a3和a5）的半正弦曲线和第二跨距（a4）的正弦曲线动态变形均方根值。锁止离合器装置（表示为常规带轮布置）和α＝0的脱开离合器装置和非线性系统比较，在横向控制模式发生共振，这些如在第一跨距Ω＝6.4（图3（a）），在第二跨距（图3（b）和（d））Ω＝3.2和7.1，在第三跨距（图3（c））Ω＝2.0。接近这些模式的激励频率限制非线性系统响应，并确定用单向离合器抑制振动的效果，肯定不发生超级和次级调波共振。当在锁止离合器装置的响应高于脱开离合器装置的情况下，如模式跨距3内Ω＝2.0和在跨距2内Ω＝3.2，非线性离合器振动被抑制。反之，如在模式跨距1内Ω＝6.4和跨距内Ω＝7.1，脱开离合器的响应较高，振动增大。

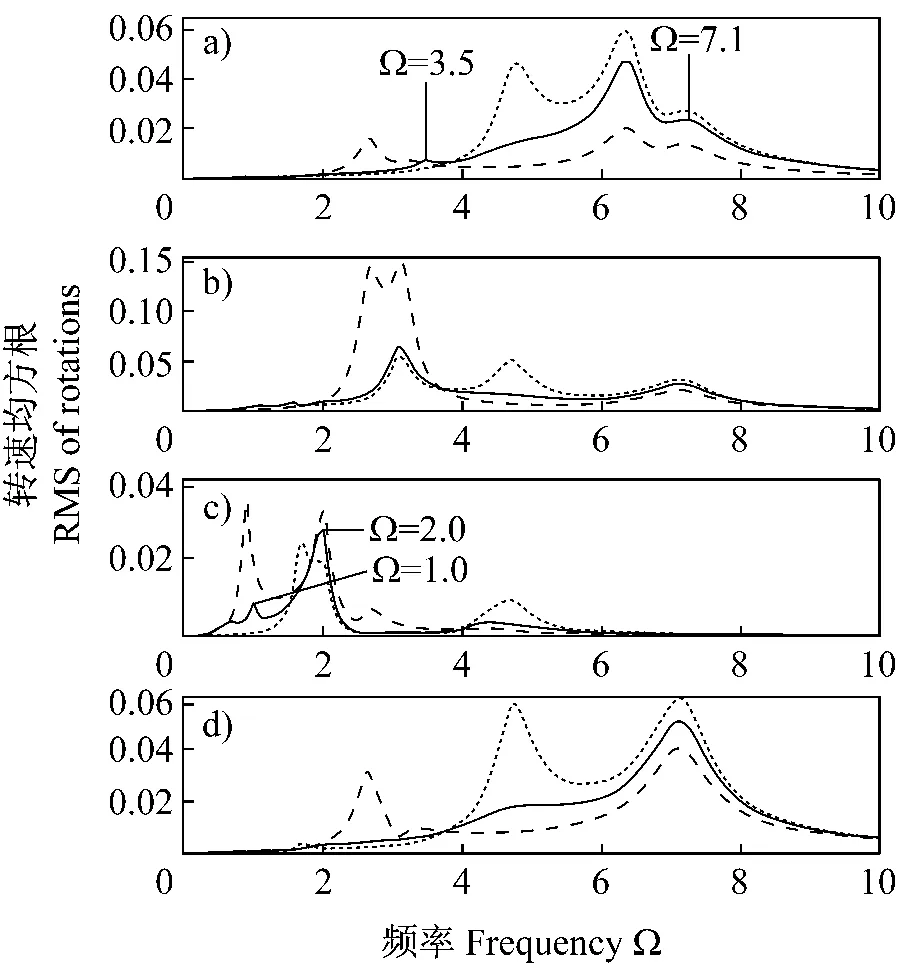
图3 对于 M1＝0.556和表2列出的其他参量，（a）a1－a1mean；（b）a3－a3mean；（c）a5－a5mean；和（d）a4－a4mean.－－锁止线性；…脱开线性α＝10；——非线性α＝10变形幅值动态响应均方根值Fig.3 r.m.s.dynamic response of the deflection amplitude for M1＝0.556and other parameters in Table 2.（a）a1－a1mean；（b）a3－a3mean；（c）a5－a5mean；and （d）a4－a4mean.－ －locked linear；…disengaged linearα＝10；——non－linearα＝10

同时，当部分循环强烈影响转动强制模式非线性脱开，如这些在Ω＝0.9和2.7（图3和4）共振比锁止离合器装置显著减小。在频率方面，脱开离合器系统有一个自然频率，但锁止离合器系统没有，如在Ω＝4.7，单向离合器使锁止离合器变成脱开离合器振动增大。

图3示在跨距横向振动中明显是超级调波共振，在跨距了Ω2＝2.0中发生强烈初级共振（图3（c））。其一可见在Ω＝1.0，发生Ω2的1階階非线性超级调波共振，其中响应频率为Ω＝2.0。同样在跨距1接近Ω＝3.5发生Ω6＝7.1的1階一y2階超级调波（图3（a））。在各个跨距，与显著的共振有关，几个其他的超级调波都具小的幅值。这些次级共振对系统动力学具有少量影响，因为它们的振幅较小。

图4示带轮和拉力器臂转动，该附件当离合器脱开时经受零刚度和自由轮而不稳定，所以它们是转动速度而不是转动如图4（d）所示。当单向离合器进行工作时，锁止离合器在Ω＝0.9时的共振消除。这表明用单向单合器能实现的有利影响。采用单向离合器在频率方面也是有效的，因为该模式有一个大的辅助转动。该具有α＝10的非线性系统可预期表明一相应增加Ω＝1.7而不是Ω＝0.9，因为具有Ω＝10的脱开系统有一个自然频率（图2），没有这样增加是明显的。同样的特性表明单向离合器的有效性是明显在Ω＝2.7对α＝10附近锁止离合器共振，对应于脱开离合器系统的自然频率在Ω＝4.7以后许可改变方向（图2）。在这种情况，具有α＝10的非线性系统表明在Ω＝4.7时共振少许提高（因为由α＝10导致的响应可以预期），但与在Ω＝2.7的利益减小相比较这种增加是很小的。采用选择一足够大的α，如α＞118。其一可避免附件一带轮在实际重要频率区Ω＝0－12内脱开离合器的共振，因此没有这样增加的回转振动产生。实际上，对有用的α范围的限制将要求单向离合器设计提出的实际速度宁可为全部发动机速度。关于附件（图4（d））当其脱开时，离合器分离，锁止离合器系统共振的消除被回转振动如这些在Ω＝0.9和2.7控制。这种分离和消除是单向离合器为何有利的主要原因。

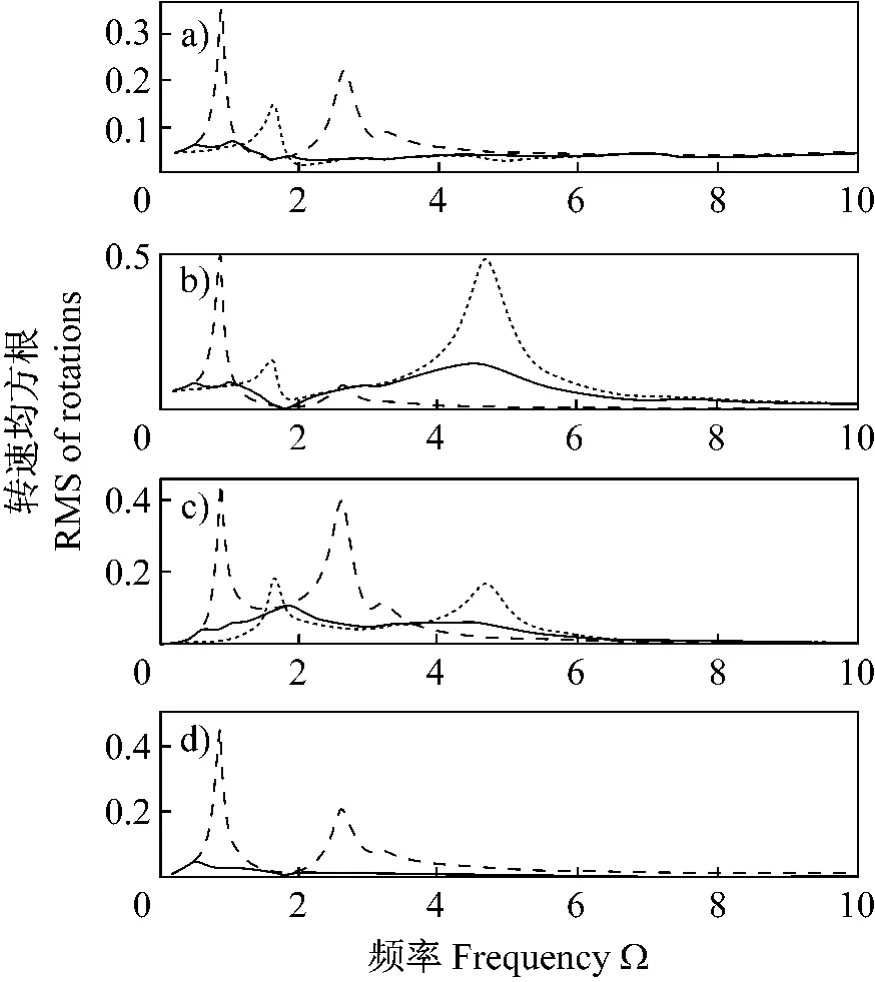
图4 动态响应均方值（a）张紧器带轮θ2－θ2mean，（b）辅助带轮θp－θpmean，（c）张紧器臂θt－θtmean和（d）附件速度˙θa－˙θ2mean，对于M1＝0.556和其他表2列的参量，－－锁止线性；…脱开线性α＝10；——非线性α＝10Fig.4 r.m.s.dynamic response of（a）tensioner pulleyθ2－θ2mean，（b）accessory pulleyθp－θpmean，（c）tensioner arm θt－θtmeanand（d）accessory velocity˙θa－˙θ2meanfor M1 ＝0.556and other parameters in Table2.－－locked linear；…disengaged linearα＝10；and——non－linearα＝10

图5示从动带轮和附件的周期速度的时间历程，以及在与不同频率有关的离合器转矩。在减速階段发生脱开，带轮和附件的运动分离。这样减速时消去了大的附件惯量对带轮的影响。当有一少许分离，两者速度就有一正弦波形。对于Ω＝0.5，离合器在循环小部分分离。对于Ω＝0.6，分离扩大并有较高激励频率的调波2Ω，3Ω等等，明显在速度谱内。图5（c）示Ω＝2.0的一个普通情况，离合器转矩由脱开的零跳到非零则作为接合开始。同样但比较明显的特性在Ω＝5.0发生（图5（d），这发生在分离的大多数循环。

离合器的接合和分离特性，导入一接合比r确定一个循环的百分比，表明该离合器是接合的。图6示α＝10和50以及表2所列其他参量经过实际重要频率范围接合比，在低的频率范围Ω＜0.5，因为少量减速，分离不发生。在高的频率范围，减速较大，大多导致脱开。预期在Ω＝1.8，因为接合系统在该频率自然有一个很小的响应（或加速／减速），故不发生脱开。单向离合器不能带来降低振动，所以不发生脱开。对于一给定的α，更多的脱开发生于脱开离合器模式共振附件，受附件一带轮如对α＝10，Ω＝4.7控制。