区域大比例尺坐标基准转换模型的研究

丁 逸，秦梦蔚

南宁市国土资源信息中心，广西南宁 530022

0 引言

国家坐标系主要有1954北京北京坐标系、1980西安坐标系、WGS-84坐标系以及CGCS2000坐标系，在实际应用当中，各种坐标系坐标系统之间的转换非常频繁。

目前坐标基准间的转换常用的方法是通过有限控制点拟合的方式得到七参数，这种方法坐标换算只能是局部应用，更重要的是普通测量用户很难获得高精度的似大地水准面差距，直接影响到转换参数以及转换成果的精度。

为此，本文采用二元双三次多项式坐标转换模型，实现区域坐标系统转换。

1 二元双三次多项式基本原理

1.1 数学模型

其中，X0、Y0为模型所使用的坐标中心；

对于每个同名点可列出观测方程为：

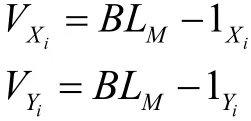
其中LM、LN为待求量；

要求解待求LM、LN 中的32个参数，最少需要32个同名坐标点。

n为观测值个数，t为必要观测值；

为避免正逆转换误差积累导致出现的不一致，采用迭代的方式实现坐标2到坐标1的逆向转换。

1.2 参数求解方法

对于模型的求解，参与解算的坐标点的数据的质量是模型是否精确的关键因素。因此，在参数求解之前，首先要对已知坐标点的精度进行验算。

主要通过比较差值和展点两种方式进行初步验证，比较差值是指将控制点在两个坐标基准下的值相减，观察该差值的大小，对于和平均值相差太大的点，说明测量误差大，需要重新进行测量或剔除；展点是指将控制点在两个坐标基准下的坐标展绘在CAD图形中，叠加影像进行大致观察。

然后对初步合格的控制点进行解算，计算残差，剔除残差较大的控制点，进行反复迭代计算，以保证最后用于计算转换模型的控制点是相容的控制点集合。

对于模型参数的求解，可在Matlab上进行求解，亦在VS2010平台上用C#语言编写了求解程序。

通过对比分析，Matlab的求解精度高10的负11次方数量级，此外，利用Matlab便于做各种误差分析。因此模型参数采用Matlab进行解算，解算版本为最新64位2010b。

1.3 精度评定

主要从三个方面来分析模型的误差:

首先分析模型的内符合精度；

其次是统计模型的中误差；

此外，利用特征点来进行外符合精度的检核，这些特征点不参与模型解算。

其中，中误差计算公式为：

当、偏大，可以确定两坐标之间的关系与模型不吻合，或是测量同名点的坐标精度太差。

2 案例计算与精度分析

2.1 工程介绍

图1

NN城市历年以来测绘基础数据采用1954北京坐标系，现需要将所有的基础数据转换到1980西安坐标系下，该城市在全国第二次土地调查时已建成的城市区域GPS C级控制网，现有该区域54坐标、80坐标、WGS84坐标以及CGCS2000坐标控制成果。

按项目要求，在原测绘基础数据控制成果中，选取适量均匀分布且有代表性的控制点与C级控制点进行联测，按E级GPS控制网要求进行外业数据采集，点位分布与观测调度如图1所示。

2.2 数据分析

采用TGO与科傻_GPS软件，按照相应技术规范、要求进行数据处理，以C级点80坐标、84坐标作为起算数据，整体解算与平差获得E级网54坐标、西安80坐标和84坐标。

E级网西安80坐标系下约束平差成果的最弱点为DG17和 EG0318，Mx为 ±0.6cm，My为 ±0.8cm， 点 位 精 度Mp=±1.0cm；84坐标系下约束平差成果的最弱点为NT0232，，Mx为±0.31cm，My为±0.40cm，点位精度Mp=±0.50cm；

为了检查控制成果的外符合精度，将为作为起算点的C级网点C0822作为检核点，将其在E级网中作为未知点平差结果与C级网坐标成果进行比较，见表1。

表1 E级网外符合精度检验

从野外采集到数据处理的流程和数据处理结果来看，本次E控制网外业观测质量可靠，内符合精度和外符合精度都比较高，各项外业观测指标都满足规范，最终成果可靠。

2.3 参数求解

将提供的所有控制点参与坐标模型计算，计算模型系数，并计算每一个控制点在X，Y方向的拟合残差，同时也计算相应的X，Y拟合值的残差中误差。

X方向拟合残差中误差为：0.0231m；

Y方向拟合残差中误差为：0.0297m。

残差分布图见图2。

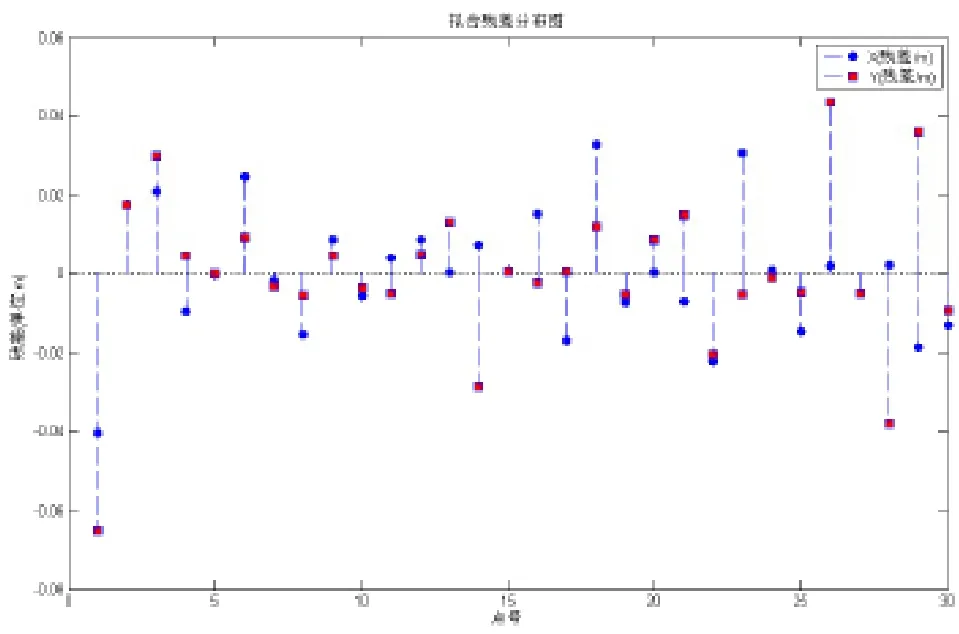
由图2可看出，拟合情况较好。多数点的残差值的绝对值小于0.02，且残差的分布服从正态分布。

此外，不存在残差超过3倍中误差的点。

为了进一步检查模型的精度，利用NN城市范围的366个特征点作为外检核点。

利用求解的模型将这些外检核点的54坐标转换为80坐标，解算的这个80坐标称为拟合值，外检核点的拟合值与其真值相减，得到拟合残差。拟合残差分布图如图3。

从图3中可以看出，外检核点的残差基本服从正态分布，除了很少一部分点的残差比较大之外，其余多数点的残差绝对值小于0.2。

各转换模型内符合精度分析：

转换基准 内符合精度中误差 最大值最小值△X △Y △X △Y △X △Y C级网2000坐标 0.00130.00130.00200.0084 -0.0114 -0.0093 C级网54坐标 0.00250.00330.01490.0210 -0.0207 -0.0168 E级网 0.02970.02310.04330.0328 -0.0650 -0.0404

各转换模型外符合精度分析：

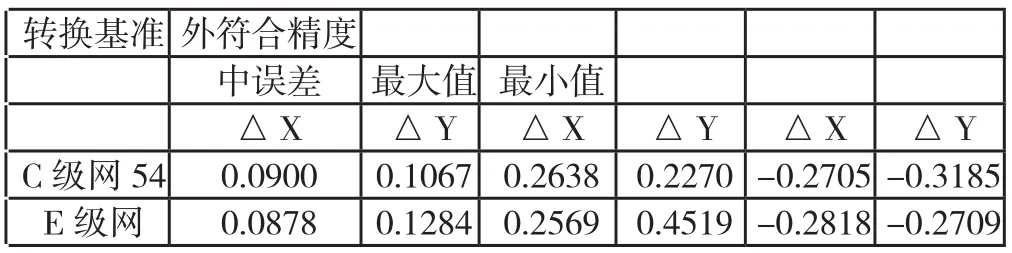
转换基准 外符合精度中误差 最大值 最小值△X △Y △X △Y △X △Y C级网54 0.0900 0.10670.26380.2270 -0.2705 -0.3185 E级网 0.0878 0.12840.25690.4519 -0.2818 -0.2709

通过对上表数据的分析，可以得出以下结论：

所有求解的模型均具有较好的内、外符合精度，中误差都控制在厘米级。

3 结论

由上述分析可知，利用二元双三次多项式模型进行区域范围大比例尺坐标基准的转换，其最大特点是可实现不同坐标系严密转换，不需要知道目标椭球似大地水准面差距就能实现坐标转换，坐标转换精度高、成果可靠。

该区域坐标转换基准参数可用于城市CORS系统，使用户实时获取不同坐标系下的坐标成果，进一步提高GPS实时动态定位技术的应用。

[1]刘基余，等.全球定位系统原理及应用[M].北京：测绘出版社，1995.

[2]郭际明.大地测量学基础[M].武汉：武汉大学出版社，2001.

[3]朱华统，杨元喜，吕志平，等.GPS坐标系统的变换[M].北京：测绘出版社，1994.