室内照度积分计算方法的改进

李必涛 杨乔 邱橘 张显宗

（暨南大学信息科学技术学院）

1 背景

有效的照明系统设计，不仅能提高室内作业舒适度，且在建立绿色节能型社会中也起着重要的作用。在建筑设计中，当线光源的长度小于计算高度的 1/4时，按点光源进行照度计算，其误差小于 5%[1]。点光源的照度计算主要有：配光曲线法[2]、等照度曲线法[1]、逐点法[2]、基于照度矩阵的计算法等[3]；当线光源的长度大于计算高度的1/4时，则必须按线光源计算。线光源的照度计算主要有：方位系数法[4]、等照度曲线法[4]、积分法等[5]。方位系数法计算线光源照度首先要鉴别五种光强分布情况，计算过程很复杂。本文在文献[5]介绍的线光源积分法的基础上，综合考虑室内各反射面及灯罩的影响，提出了一种改进方法。通过实验数据的比较，改进后的计算误差大幅减少。

2 线光源积分法

前提与假设：

(1)教室、图书馆等公共空间室内照明光源大多采用日光灯组，组内每根灯管之间的横向距离相对于被照面到光源的距离很小，所以此时将日光灯组简化成线光源，简化后的光通量等于组内日光灯管的光通量之和；

(2)不考虑空气透射率的影响，空气透射率默认为1；

(3)不考虑自然光对工作面照度的影响。

在三维空间中，线光源的光照模型如图1所示。平行平面为经过线光源纵轴和发光平面法线的平面，垂直平面为经过发光平面法线且垂直于线光源纵轴的平面。 I0为线光源发光面法线方向上的光强，Iα为平行平面中与 I0成α角的光强，Iθ为垂直平面中与I0成θ角的光强。

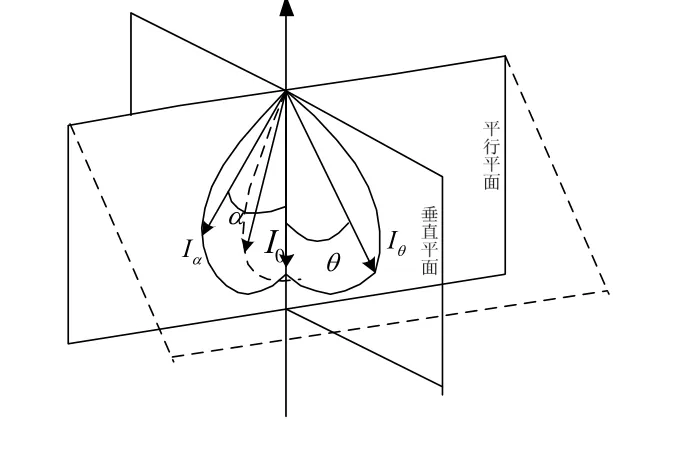
图1 线光源的光强分布曲线

线光源照度计算示意图如图2 所示，xy表示工作面所在平面，线光源的中点经过z轴且和x轴平行，线光源到工作面的高度为0h，线光源的长度为0l，光通量为φ。

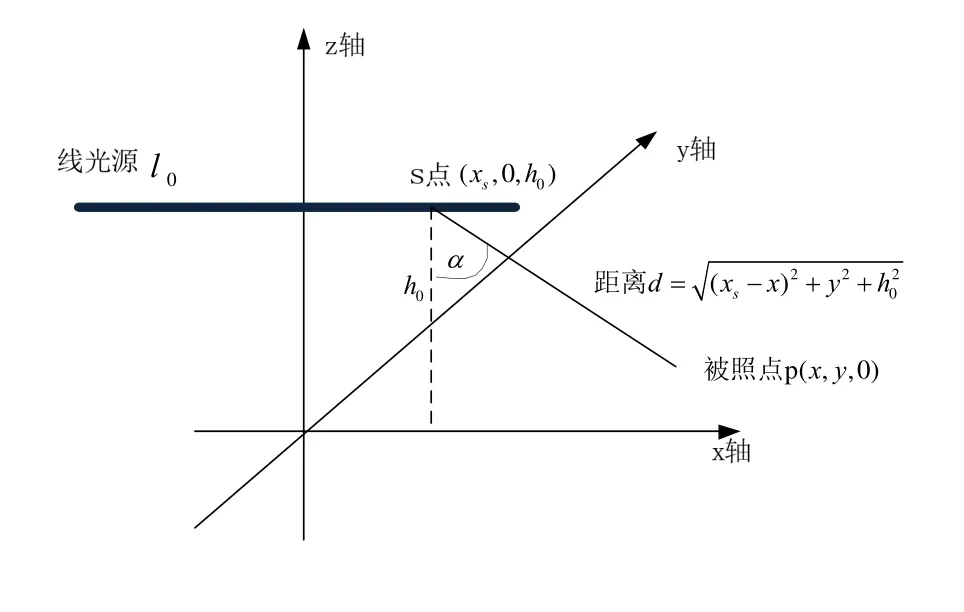
图2 线光源照度计算示意图

在线光源上任取一点S（xs,0,h0）点，在工作面上任取一点P(x,y,0)，S点到P点的距离为：

S点与P点的连线和被照面的法线的夹角为α，其余弦值为：

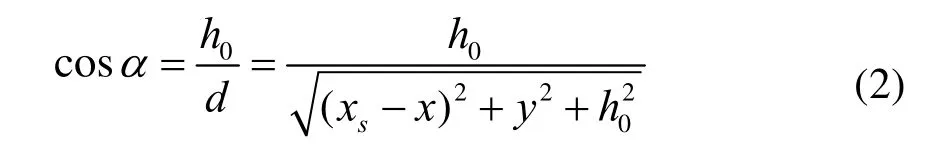
根据假设条件，S点为点光源，因此S点对P点的照度符合点光源的球面辐射规律。被照点P(x,y,0)相对于S点的照度为：

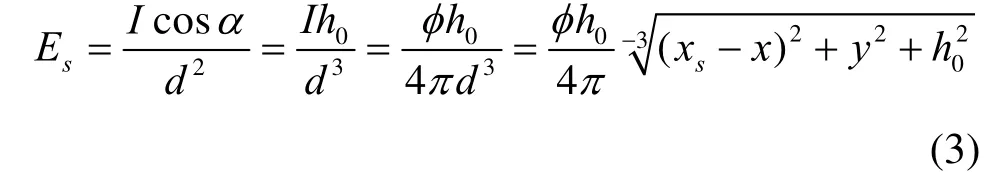
整个线光源对P点的照度为：

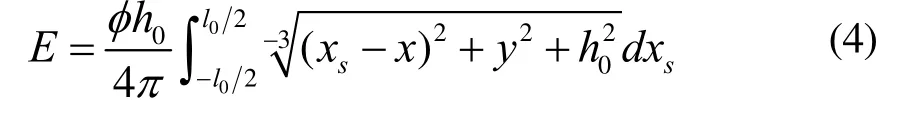
3 计算结果的实验比对

3.1 实验测量

选择教室一间，其主要参数如下：长×宽×高：1293××(单位：m)，教室中安装9个灯组，每个灯组中安装3盏T5型28W的荧光灯，每盏荧光灯的额定光通量为2900lm。表1为室内照明相关参数，表2为T5型日光灯的相关数据[6]。

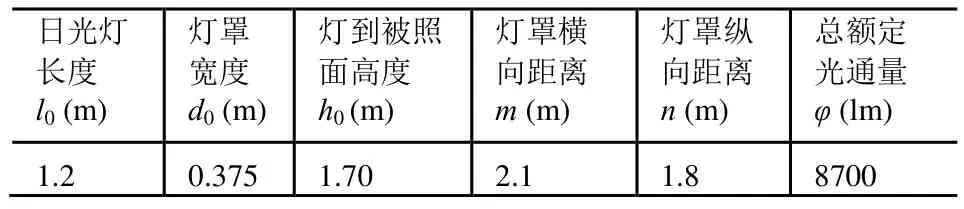
表1 室内照明相关参数

表2 T5系列荧光灯相关数据

照度计型号：LX-1010BSS数字式照度计。

荧光灯照度区域分布图如图3 所示：以日光灯中心点为坐标系原点建立坐标系，在区域三内建立12×16个网格，网格间距为0.2m，测出网格点的照度值，如表3所示。

图3 荧光灯照度区域分布图（俯视）

表3 理论数据与实测数据

3.2 计算结果与实验数据比对

采用式（1）～式（4）计算网格节点上的照度值。如表3所示：其中，照度E1为积分法的计算结果，照度E2为实验测得的数据，|E1-E2|为同一坐标上计算结果与实测数据的误差。

从图3 和实验测得的数据比较中可以看出，在随机选取的十个数据中，积分法有五个误差在 100到150左右，其中最大的达到145。而且误差本身的大小变化也比较明显，误差幅度在9.1～145。一般情况下照度计算允许的误差为-10%～20%，积分法的计算误差较大。上述积分方法的应用只考虑到线光源直射照度对于工作面的影响，实际上工作面的照度不仅受直射光的影响，还应考虑灯罩、室内墙面、顶棚、地板、自然光等因素对于工作面照度的正向作用。

4 照度积分方法改进

各个反射面对于被照点的影响相当于在原来的基础上增加了光源。在各个反射面中，灯罩由于位置最靠近光源，而且灯罩材料的反射系数是所有影响因素中最大的。因此，灯罩对被照点的影响最大，可以单独计算。墙面、顶棚和地板等因素对于被照点的影响可以在传统积分法的基础上增设一个修正因子β。

空间直角坐标的位置不变，在灯罩上任取一点t(x1,y1,h1)，工作面上任取一点P(x,y,0)，t点到P点的距离为：

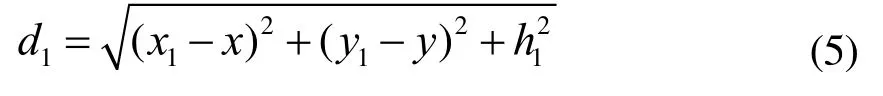
点 t与点 P的连线与工作面法线的夹角的余弦为：

点P受灯罩上点t的照度为：

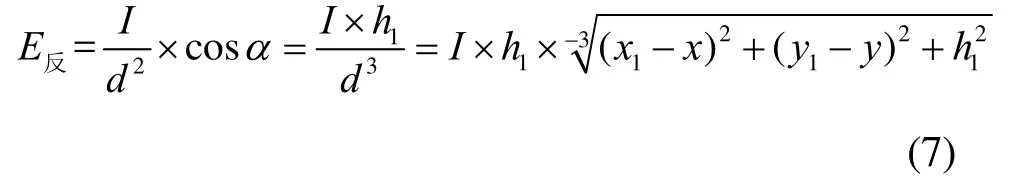
为了简化计算，可将灯罩看成是平面反射，平面的长度为灯罩的长度，平面的宽度为灯罩的外围等效宽度，则反射照度即整个灯罩对点P的照度为：

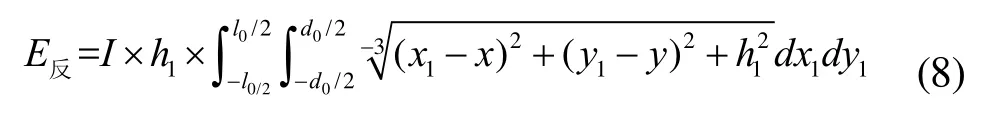
总照度为直射和反射照度之和，即：

由于灯罩反射光只向下辐射，此时计算光强I的立体角为2π，式(9)可化为：

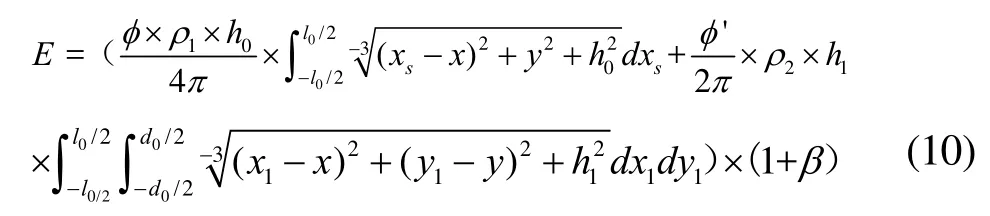
式(10)中：1ρ表示荧光灯因为日常老化、表面灰尘等因素影响而导致的光通量减少；2ρ表示荧光灯光辐射能量在灯罩上的损耗，即灯罩材料的反射系数，1ρ和2ρ的取值都在0～1之间；1h表示灯罩到被照面的高度，由于灯罩到光源的距离相对于光源到被照面的距离可以忽略不计，所以 h1≈h0。则照度为：

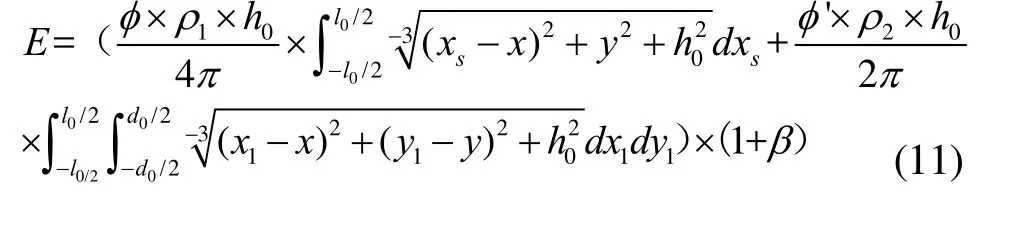
图4所示为灯罩的横截面，荧光灯与灯罩末端的夹角为δ，不考虑在空间传播过程中的光损耗。假设荧光灯的光线向四周呈均匀辐射，则灯罩接受到的光通量与δ角有关，其光通量为：

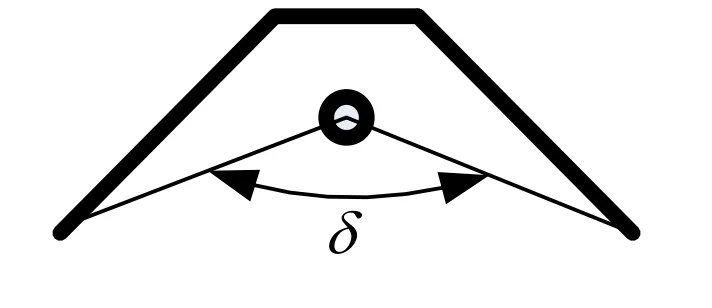
图4 灯罩横截面示意图

于是，上式转化成关于β的方程，记为：

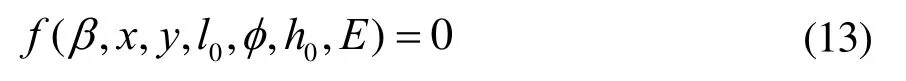
由于自然光的变化范围较大，且很难人为控制，所以在假设条件中，β的确定并没有考虑自然光对工作面照度的影响，影响β取值的有顶棚、地板、墙面等反射面因素，这些因素在实际中的取值一般都比较固定，因此该方法具有一定的实用性。

表4 β值计算结果

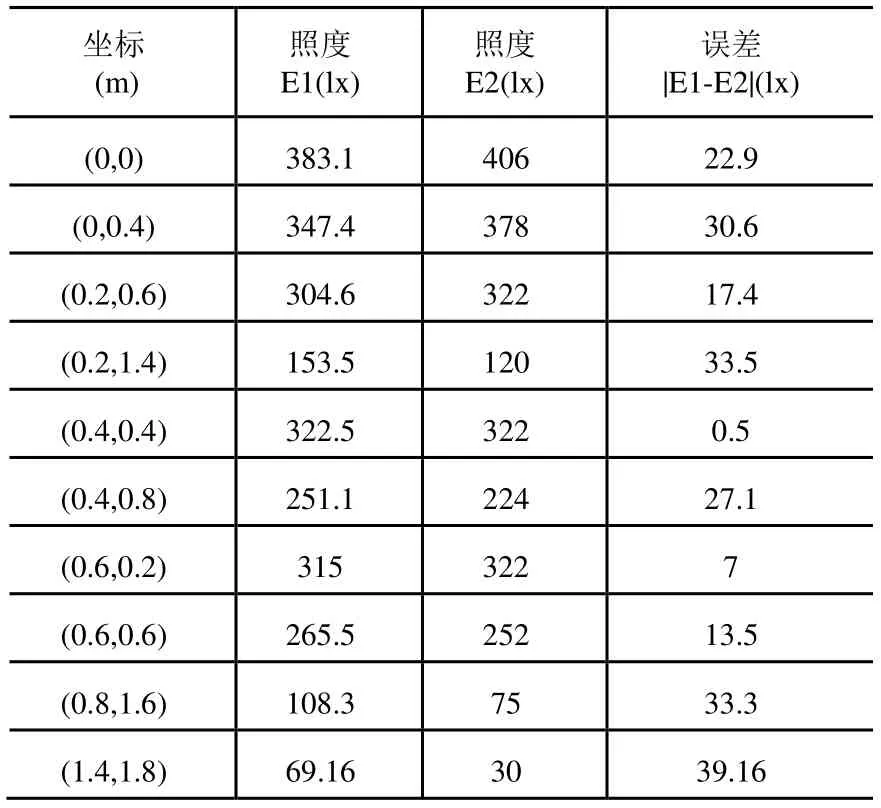
表5 改进后的理论数据与实测数据

由以上数据可以看出，采用新方法误差明显减少很多，最大误差减小至 39.16，而且误差的变化幅度也比改进前要小，较原来方法有明显的改进。

5 结论

方位系数法和等照度曲线法进行等照度计算的运算过程需要人工判断，而且很难模拟出整个室内的照度状况，因此适用于单点的精确计算；单纯的对线光源进行积分，没有考虑到室内其它影响照度的因素，计算误差比较大，但作为一种理论依据，给线光源照度计算提供了一个方向；改进后的光源积分法，综合考虑了灯罩和墙面等其它因素的影响，在很大程度上减小了误差。

[1]中国建筑学会建筑电气分会.建筑照明[M].北京:中国建筑工业出版社,2010.

[2]李运江,彭惠明,徐波.几种照度计算方法的比较与研究[J].三峡大学学报,2003(2): 30-32.

[3]丁新东,姚加飞,张玉兰.一种点照度计算方法[J].照明工程学报,2007(12): 48-50.

[4]周太明,等.高效照明系统设计指南[M].上海:复旦大学出版社,2004.

[5]秦玉玺.线光源辐照度的计算[J].红外技术,1990(12): 43-44.

[6]M.戴维.埃甘,维克多.欧尔焦伊著,袁樵译.建筑照明[M].北京:中国建筑工业出版社,2006.