高职院校全面质量管理系统的模型分析*
2012-07-05周茂东严俊田森平
周茂东 严俊 田森平
(1.广东女子职业技术学院 2.华南理工大学自动化科学与工程学院)
1 引言
全面质量管理(Total Quality Management,TQM)是20世纪90年代西方教育管理理论与实践的热点,是广泛应用于工商、交通运输、邮电、金融、卫生等行业的全新企业管理理论与方法[1],已有许多学者对TQM 的理论和方法进行了较深入的研究[2~4]。TQM的管理理念和管理技术已在我国一些本科高校应用,取得了较满意的效果。
从发展规模来看,全国独立设置的高职院校数量已占普通高校总数的一半以上,高职院校的在校学生人数在普通高校中占相当大的比例(已接近普通高校在校生的一半)[5]。在此背景下,如何保证高职院校的教育质量使之适应社会经济的发展是迫切需要解决的问题。随着我国高职教育对质量问题的关注,学术界开始关注在高职院校的教学管理过程中融入TQM 的思想和理念,并发表了如何在高职院校实施TQM的研究成果[6~8]。目前,我国高职院校经费不足已成为其教育数量发展、质量提高的瓶颈因素。因此,高职院校实施TQM的核心是强调以最小的成本投入获得最优化的效益和效率。有学者从不同角度构建了高职院校实施TQM数学模型[9,10],试图结合定量的方法分析实施TQM对提高我国高职院校的办学质量的影响。
本文以高职院校实施全面质量管理问题为研究对象,建立了描述高职院校TQM投入和效益关系的状态空间模型,旨在用数学模型研究投入和效益之间的内在联系,实现TQM效益的最大化。
2 数学模型的建立
设高职院校TQM投入和TQM效益的变化是相对均匀的,以 x = x(t)和 y = y(t)分别表示时刻t的TQM投入量和TQM效益值,并假设 x(t)、y (t) 是t的连续可导函数,则 x(t)和 y(t)对时间t的相对变化率应与x和y的大小有关。因此,高职院校的TQM投入和TQM效益之间的关系可用如下的Kolmogorov模型来描述:

其中 f(x,y)和 g(x,y)是 x(t)和 y(t)的连续函数,分别称为x和y的相对变化率。
当f(x,y)和 g(x,y)为一般非线性函数时,研究系统(1)的定性特性比较复杂,但当 f(x,y)和g (x,y)取一些特殊形式时,已经有研究成果[11,12]。如文献[11]研究的系统:
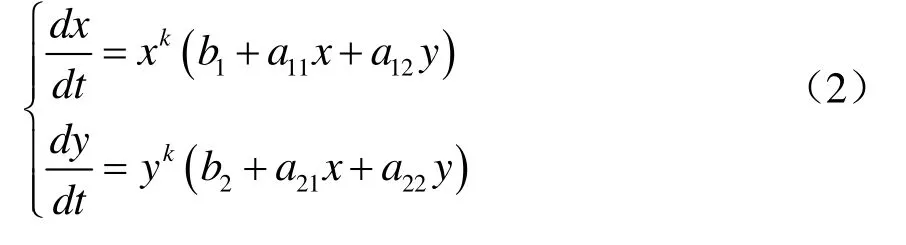
该系统给出了 1k= 时系统(2)具有4个有限平衡点的全局拓扑结构图。进一步,文献[12]利用系数之间的不等式给出了 1k= 时系统(2)少于4个有限平衡点的全局拓扑结构图。此外,对于 3k= ,文献[12]研究了系统(2)极限环的存在性问题,得到了较大范围的无环性条件。
对系统(1)中的函数 f(x,y)和 g(x,y)进行线性化,可得到:
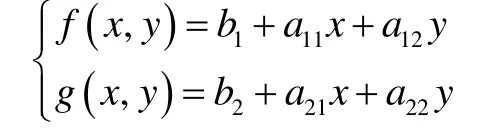
则系统(1)可写成如下形式的Lotka-Volterra模型:
首先,用与离心机配套的环刀在不同样地中取土,取样土层为0~20 cm,土样风干后经直径2 mm的筛孔过筛,利用环刀法测定土壤的容重;将用环刀取得的原状土经蒸馏水浸透48 h直至饱和,并称重;将饱和的原状土样和扰动土样放入离心装置中,设定离心机转速分别为0、500 r/min、1000 r/min、1500 r/min、2000 r/min、2500 r/min、3000 r/min、4000 r/min、6000 r/min、8000 r/min,在每次压力达到平衡后取出土样进行称重,并用游标卡尺测量土面到环刀顶面的高度,以此确定土样收缩和容重变化。
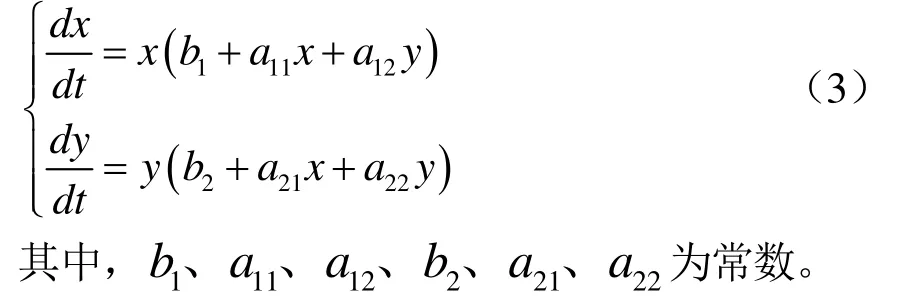
b1为TQM投入增长率,指实施TQM投入的增长率,若投入逐年增加,则 b1> 0;若投入逐年减少,则 b1< 0。一般情况下,高职院校实施TQM会有一个认识和探索过程,其投入会由少到多逐年增加。
a11为投入制约系数。一定的 TQM 投入,会带来一定的TQM效益,但TQM投入达到某一水平后,其它因素就会制约TQM效益的增加,由于资源的限制,不可能使投入无限地增长,投入必须有一个最大限度, a11就是表示这个限度的量,取 a11< 0。
a12为TQM的实施效果增加对TQM投入的影响系数。a12> 0表示TQM效益对TQM投入具有促进作用; a12< 0反之。
b2为TQM效益的固有增长率。对TQM进行投入时,会促进TQM效益的增加,取 b2> 0。
a21为TQM投入对TQM效益的影响系数。由于TQM投入对效益是促进作用,故取 a21> 0。
a22为效益制约系数。在TQM系统中,TQM效益不可能无限增加,会有一个限度,22a 就是表示这个限度的量,取220a < 。
3 模型的动态分析
下面分析模型(3)的稳定性和定性特征。方程组(3)所描述的系统有4个平衡点,分别为: P1(0,0),
平衡点P1和P2对应TQM系统的投入都为0,没有实际意义。
平衡点P3表示进行了一定的TQM投入,但TQM效益为0,这种情况对于早期实施TQM较为常见,由于刚开始实施TQM,效益不明显或完全失败。
平衡点 P4对应的情况是正常的结果,在高职院校进行一定的TQM投入,就会产生一定的TQM效益。下面对这种情况进行分析,由于TQM投入和效益都是正的,只需要在第一象限分析P4的形态即可。
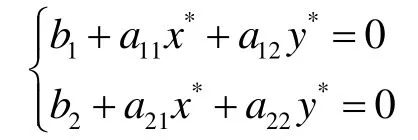
模型(3)在()**4,Pxy的线性化系统的系数矩阵为:

因此,()**
4,Pxy渐近稳定的充要条件为:

上述渐近稳定性结果是局部的,关于()**4,P x y 的全局渐近稳定性问题,有如下结果[13]:
定理 1:方程组(3)不可能存在极限环和奇异极限环,即不可能存在动态平衡。
定理1说明描述高职院校TQM系统的模型(3)是一个非动态平衡系统。
定理2:模型(3)的正平衡点为全局渐近稳定的充要条件为:
③110a < ,220a < ,即TQM投入和效益不可能是无限增长的。
P1(0,0) 是不稳定结点,是鞍点(不稳定)。进一步分析模型(3)无穷远奇点的性质[11],可得模型(3)的全局结构图如图 1所示(由于TQM 投入与效益都是正的,所以只画出第一象限的全局结构图)。
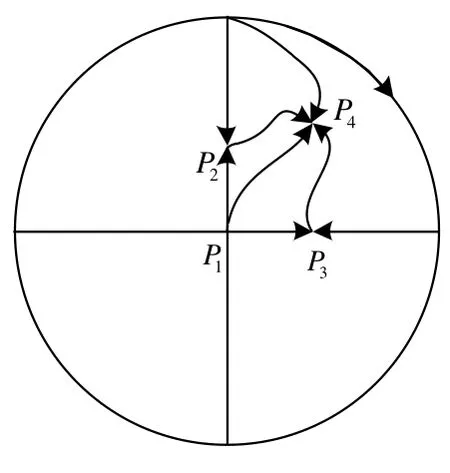
图1 系统(3)的全局结构图
定理2和图1表明在高职院校实施TQM过程中,不同的 TQM 投入会带来不同的 TQM 效益,增加TQM 投入虽然会带来效益的增加,但效益不会无限制的增加,而是达到某个最大化的状况,此时 TQM系统达到一个平衡状态,平衡点 P4的坐标对应平衡状态的位置。
4 结论
本文分析了在高职院校实施TQM系统的问题,建立了描述TQM系统的数学模型,利用该模型分析了TQM投入与TQM效益之间的演变规律。此外,对所给模型进行了比较详细的稳定性和定性分析,给出了系统的全局结构图。分析表明,虽然TQM系统是一个非动态平衡系统,但在演化过程中可近似达到一个平衡状态,该平衡状态对应TQM效益的最大化。
[1]刘立户.全面质量管理[M].北京:北京大学出版社,2004.
[2]高阳,王刚.模糊AHP模型在商业银行全面质量管理综合评价中的应用[J].统计与信息论坛,2004,19(1):9-12.
[3]常金玲.基于 PDCA的信息系统全面质量管理模型[J].情报科学,2006,24(4):584-587.
[4]宋永涛,苏秦,彭晓辉.全面质量管理系统的动态演化模型[J].科技管理研究,2008,8:209-211.
[5]周劲松,肖智清.基于全面质量管理的高等职业教育质量评价模型的建设[J].职业教育技术,2008,8:5-6.
[6]刘萍.全面质量管理理论在高等教育质量管理中的应用[J].科技与管理,2009,11(4):143-148.
[7]衣海霞.全面质量管理在高等教育领域的应用及研究述评[J].现代教育管理,2010,8:58-61.
[8]陈申华,王柱京,龙承建.论高等教育全面质量管理[J].国家行政学院学报,2010,3:64-67.
[9]王传斌.基于联系数的高职院校教师教学执行力评价数学模型[J].数学的实践与认识,2010,40(22):71-77.
[10]阮杰昌,王甫茂,李应.评价高职院校办学规模与教育教学质量关系的数学模型[J].职业时空,2010,6(12):143-144.
[11]蔡燧林.一类二次系统的全局定性分析[J].浙江大学学报,1979,4:114-122.
[12]田森平.一类Kolmogorov模型的定性研究[D].武汉:华中师范大学学位论文,1988.
[13]陈兰荪,孟新柱,焦建军.生物动力学[M].北京:科学出版社,2009.
