多级轴流压气机变几何扩稳优化与性能约束分析
2012-07-05吴虎毛凯孙娜
吴虎,毛凯,孙娜
(西北工业大学动力与能源学院,西安 710072)
多级轴流压气机变几何扩稳优化与性能约束分析
吴虎,毛凯,孙娜
(西北工业大学动力与能源学院,西安 710072)

吴虎(1963),男,教授,博士生导师,研究方向为燃气轮机气动热力学。
为了提高多级轴流压气机在非设计条件下的稳定裕度,基于逐排基元叶片方法,应用恰当的损失和落后角模型,建立了预测多级轴流压气机特性工程方法,并将其与复合形优化方法相结合,给出了1种多级轴流压气机多静叶排调节扩稳算法,并应用于NACA 8级轴流压气机,取得了明显扩稳效果,数值计算进一步阐明了不同性能约束对变几何扩稳效果影响规律。结果表明:应用合理的性能约束进行优化,对提高多级轴流压气机非设计条件下稳定裕度有明显效果。
轴流压气机;性能;变几何;气动稳定性;优化;航空发动机
0 引言
现代航空发动机所采用的新型轴流压气机具有超/跨声速、压比高、效率高的特点,设计新型、高效和宽稳定工作范围的轴流压气机对于提高整台发动机的性能具有重要意义[1-7]。尤其是军用航空发动机的宽飞行包线和超机敏姿态以及快速改变状态(急动加、减速)对其压缩系统宽稳定范围要求日趋苛刻[8-11]。众所周知,当多级轴流压气机处于部分转速状态时,会出现“前重后轻”,而在高转速状态下,后面级则是出现不稳定的关键级。因此,长期以来,在多级轴流压气机使用过程中普遍采用调节压气机导叶与静叶排安装角对其实施气动扩稳。英国和巴西等国已在这一领域开展了卓有成效的研究工作,并取得了一系列重要成果[12-13]。
本文紧跟国外技术的最新进展,对新型多级轴流压气机进行研究。
1 模型方程
1.1 逐排基元叶片模型
为实施多级轴流压气机多变量变几何扩稳,文献[2]采用逐级近似模型技术,但该技术明显限制了静叶排安装角调节范围。为此,本文基于文献[14]采用逐排基元叶片准1维模型,其基本控制方程为
流量连续方程

式中:m为流量;ρ为密度;Vz为轴向速度;S为面积。
能量方程绝对坐标系下

相对坐标系下

式中:Lu为轮缘功;cp为气体定压比热;T为静温;T*为总温;u为轮缘速度;h为静焓;h*为总焓;W为相对速度;下标1为叶排进口;下标2为叶排出口;下标w为相对坐标系下的值。

状态方程式中:R为理想气体常数。
具体求解过程,所有参数均为叶片平均半径处的气动参数。
(2)根据所选定的参考攻角模型,计算出参考攻角i*。
(3)根据选定的损失与落后角模型,计算出转子出口的总压和总温等。
(4)根据计算出的转子出口参数,计算出转子出口处的流量,判断进出口流量是否连续,如果不满足连续,则回到第3步继续计算;如果满足要求,则将转子出口的条件作为静子进口的条件,重复(2)~(4)的步骤,直至算出该级的压比π和效率η等。
(5)将该级静子的出口参数,作为下一级转子的进口参数继续计算。
首先,对逐排基元叶片模型中所需要输入的流动损失和落后角参数模拟技术进行了归纳和整理,本文算例用NACA 8级轴流压气机[15-16],该压气机的前2级为跨声速,转子叶型为双圆弧型,静子叶型为NACA 65系列叶型;后面6级为亚声速级,转子和静子叶型均为NACA 65系列叶型。
经过详细计算、分析和筛选,确定出预测其特性的应用模型,见表1。其中,喘振点估计方法采用Howell所给模型[17],计算值与试验值的对比如图1、2所示。

表1 8级轴流压气机性能预测使用的各模型

图1 8级轴流压气机流量-压比性能曲线

图2 8级轴流压气机流量-效率性能曲线
从图1、2中可见,采用表1所确定的损失和落后角模型来预估8级轴流压气机的总性能曲线,结果比较满意,特别是在100%和90%设计转速时,计算值与试验值吻合较好。但是,在80%、70%、60%和50%实际转速下时,压比和效率较之试验值都有些偏大,尤其是效率特性曲线,见表2。这主要是由于部分转速状态偏离设计状态较远,相应的损失和落后角关联存在一定的不确定性。另外,从表2中可见,预测结果虽然有2%左右的偏差,但在超过设计转速70%以上工况下,其不稳定工作点上的压比和流量预测值与试验值的符合程度较好。

表2 8级压气机各转速状态下的喘振点预测值与试验值比较
1.2 多变量变几何扩稳模型
本文优化算法采用文献[18]给出的复合形法。该方法是把Box求解无约束优化问题的单纯形法推广到求解如下的约束优化设计的1种方法。

所谓复合形是指在n维空间的可行域R内,由k(k=n+1~2n)个顶点所构成的多面体。通过对可行域内多面体顶点目标函数值的比较,不断地去掉坏点,代之以既能使目标函数值下降又满足所有约束条件的新点,这样通过顶点的不断更迭而使复合形发生形变和移动,并逐渐逼向最优点。由于对复合形不必保持规格图形,顶点数较多,因此可以求解非线性的约束问题,而且计算稳定可靠,但不能用于解含有等式约束的问题。
以下给出对8级轴流压气机第4级静叶排独立调节扩稳优化计算结果。
(1)8级压气机工作在80%设计转速下的扩稳优化。

优化目标为a.无性能约束时自变量约束条件为
20≤Δβ1≤35;11≤Δβ2≤20;7≤Δβ3≤12;3≤Δβ4≤6
b.具有性能(压比)约束(约束1)Prstall≥5.50时自变量约束条件同a步骤。
c.具有性能(压比)约束(约束1)Prstall≥5.65时自变量约束条件同a步骤。
(2)8级轴流压气机工作在70%设计转速下的扩稳优化。

优化目标仍为a.无性能约束时自变量约束条件为
20≤Δβ1≤35;11≤Δβ2≤20;7≤Δβ3≤12;3≤Δβ4≤6
b.具有性能(压比)约束(约束1)Prstall≥4.15时自变量约束范围同a步骤。
c.具有性能(压比)约束(约束1)Prstall≥4.30时自变量约束条件同a步骤。
式中:Δβi分别为第i排静叶排安装角变化量(°);Q、Pr分别为换算流量(kg/s)、增压比和绝热效率;下角标stall为喘振点值。
在80%设计转速工况下,无性能约束和2种不同性能约束对第4级静叶调节扩稳影响如图3、4所示。很明显,在扩稳优化时,随着约束性能的提高,调节后的不稳定点换算流量逐渐增加,表明稳定工作裕度相应减小,扩稳效果降低,但优化后的性能明显提高。在几何不调节时预测的不稳定点效率为0.9202最大效率为0.9264,在无性能约束调节时预测的不稳定点效率为0.8748,最大效率为0.8763,性能约束1下预测的不稳定点效率为0.8827,最大效率为0.8877;在性能约束2下预测的不稳定点效率为0.8920,最大效率为0.8973。这表明,在压气机变几何扩稳调节中对其压比性能作适当约束不仅能改善压比特性,而且也能明显降低流动损失,增加其绝热效率。在不同约束条件下,优化后的各静叶排安装角调节量及对应不稳定点参数分别为:
(1)无约束时
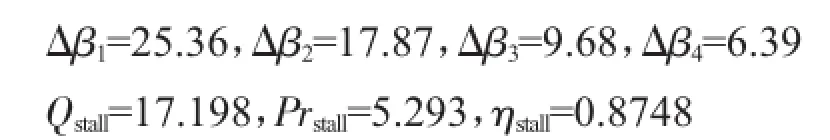
(2)性能约束1时

(3)性能约束2时

在70%设计转速工况下,无性能约束和2种不同性能约束对第4级静叶调节扩稳影响如图5、6所示。很显然,该状态下的结果与80%设计转速对应结果相类似,带性能约束的优化调节不仅在改善压比特性的同时明显降低流动损失,增加其绝热效率。在不调节时,预测的不稳定点效率为为0.909最大效率为0.9184,在无性能约束调节时预测的不稳定点效率为0.881,最大效率为0.893,在性能约束1下预测的不稳定点效率为0.901,最大效率为0.9074;在性能约束2下预测的不稳定点效率为0.9038,最大效率为0.9134。

图3 80%设计转速下变几何流量-效率特性

图4 80%设计转速下变几何流量-压比特性

图5 70%设计转速下变几何效率特性

图6 70%设计转速下变几何压比特性
在不同约束条件下,优化后的各静叶排安装角调节量分别为:
(1)无约束时

(2)性能约束1时

(3)性能约束2时

由此可见,在无性能约束下的各静叶排安装角调节范围最大,致使调节后不稳定工作点上换算流量最小;随着约束性能的提高,优化后的各静叶排安装角调节范围逐渐减小,这种变化规律十分符合叶轮机工作原理所阐述的多级压气机在低换算转速下扩稳实施的导叶/静叶调节规律。
进一步比较可见,对于80%和70%设计转速,在无性能约束和2种不同性能约束下,第4级静叶调节扩稳优化后的调节规律相同。文献[19]给出某型先进涡扇发动机第9级高压压气机在84%设计转速以下调节导叶/静叶安装角扩稳采用了相同的变几何调节规律。很明显,这与本文优化结果相一致。
2 结论
(1)通过详细整理、分析和筛选,发展出了比较合理的某型多级轴流压气机特性预测模型及方法。
(2)将逐排基元叶片模型与复合形优化方法进行了有机结合,发展了多级轴流压气机多变量变几何扩稳方法,并成功地对某第8级轴流压气机进行了扩稳优化,取得了明显效果。
(3)当实施无性能约束变几何优化调节,优化后的各静叶排安装角调节范围最大,对应压气机不稳定工作点换算流量最小,表明其扩稳效果最好;随着约束性能的提高,优化后的各静叶排安装角调节范围逐渐减小,对应压气机不稳定工作点换算流量也逐渐增大,扩稳效果降低,但调节后性能得到明显改善。
(4)对于80%和70%设计转速,实施对第4排静叶安装角独立调节扩稳优化结果表明,无论是有或无性能约束,其扩稳的变几何调节规律都相同,这与某型发动机高压压气机变几何扩稳调节规律相一致。
[1]AGARD.Variable-geometry and multicycle engine[R]. AD-A-040189,1976.
[2]Orkisz M,Stawarz S.Modeling of turbine engine axial-flow compressor and turbine characteristics[J].Journal of Propulsion and Power,2000,16(2):131-136.
[3]Roy-Aikins J E A.Considerations for the use of variable geometry in gas turbines[R].ASME 90-GT-271.
[4]Oates G C.Aircraft propulsion systems technology and design [M].New York:AIAA Education Series,1989:58-72.
[5]Kimzey W F.An Analysis of the influence of some external disturbance on the aerodynamic stability of turbine engine axial flow fans and compressors[R].AEDC-TR-77-80,1997.
[6]Klepper J.Technique to predict stage-by-stage,pre-stall compressor performance characteristics using a streamline curvature code with loss and deviation correlations[D]. Knoxville:University of Tennessee,1998.
[6]吴虎,廉小纯.轴流压气机稳定性预估的改进模型[J].西北工
业大学学报,1995,13(1):129-133.
[7]Gill M E,Elder R L.A surge prediction method for multi-stage axial-flow compressors[J].Institution of Mechanical Engineers,1984,198(4):13-18.
[8]Escuret JF,Elder R L.Active control of surge inmulti-stage axial-flow compressors[R].ASME 93-GT-39.
[9]张健,任铭林.静叶角度调节对压气机性能影响的试验研究[J].航空动力学报,2000,15(1):27-30.
[10]夏联,崔健,顾扬.可调静叶对压气机低速性能影响的试验研究[J].燃气涡轮试验与研究,2005,18(1):31-34.
[11]Sun J,Elder R L.Numerical optim ization of a stator vane setting in multistage axial-flow compressors[J].Power and Energy,1998.212(3):35-39.
[12]Bringhenti C,Barbosa J R.Methodology for gas turbine performance improvement using variable-geometry compressors and turbines[J].Power and Energy,2004,218(3):18-23.
[13]White N M,Touridakis A,Elder R L.Axial compressor performancemodelingwith aquasi-one-dimensionalapproach [J].Power and Energy,2002,216(2):45-48.
[14]Voit C H.Investigation of a high-pressure-ratio eight-stage axial flow research compressorwith two transonic inlet stage I aerodynamic design[R].NACA-RM-E53I24,1953.
[15]Geye R P,Budinger R E,Voit C H.Investigation of a high-pressure-ratio eight-stage axial-flow research compressor with two transonic inlet stageⅡprelim inary analysis of overall performance[R].NACA-RM-E53J06, 1953.
[16]Howell A R,Calvert W J.A new stage stacking technique for axial flow computer performance prediction[R].ASME 78-GT-139.
[17]陈立周.机械优化设计方法[M].3版.北京:冶金工业出版社,2005:55-63.
Ana lysis o f Variab le Geom etry Aerodynam ic Stability Op tim ization and Perform ance Constraints for Mu ltistage Axia l-flow Com p ressor
WU Hu,MAO Kai,SUN Na
(SchoolofPowerand Energy,Northwestern PolytechnicalUniversity,Xi'an710072,China)
In order to improve the stabilitymargin atoff-design conditon ofmultistage axial-flow compressor,the engineeringmethod for calculating multistage axial-flow compressors performances was built based on blade row-by-blade row cascade method and an appropriate loss and deviation models.Combined with comp lex optim ization method,an aerodynam ic stability numerical methodology of stator stagger setting ofmultistage axial-flow compressor was established and applied to NACA eight-stage transonic axial compressor to obtain obvious aerodynamic stability effectiveness.The influence rules of different performance constraints on variable geometry aerodynamic stability effectiveness were clarified further by the numerical calculation.The result show that the multistage axial-flow compressors isoptimized by the reasonable performance constraints to improve obviously the stabilitymargin atoff-design conditon.
axial-flow compressor;performance;variable geometry;aerodynamic stability;optimization;aeroengine
2012-06-16
