逻辑代数化简的计算机实现

耿 强 黄雪琴

（1.海口经济学院信息工程学院 海南 海口 570203；2.海南经贸职业技术学院信息系 海南 海口 571127）

0 引言

在实际的电路设计中,往往要根据逻辑函数要求，归纳出表达式及画出相应的逻辑电路。但直接得出的表达式往往不是最简形式,这样会使电路复杂,所需电子元器件也随之增加。因此需对逻辑代数进行必要的化简,使每个逻辑单元相对简单化、合理化。

通常,人们采用代数法和卡诺图法化简。用代数法化简需熟练掌握逻辑代数的基本定律,而且需要一些化简技巧,特别是每次经代数法化简后，得到的表达式是否为最简式较难掌握。卡诺图法虽然可以解决上述问题,但卡诺圈易圈漏、圈错或产生逻辑覆盖。为消除这种人为引起的错误,本文提出基于卡诺图原理用计算机编程实现逻辑代数化简的方法。而本文着重分析的是其中“化简逻辑代数”的部分。它对于整个化简过程有着承上启下的作用。

1 卡诺图化简的基本原理

笔者按照列表法的化简思路来进行分析，而列表法化简源于卡诺图法化简，因而在此介绍一下卡诺图化简的原理。

卡诺图是逻辑函数的一种图形表示。一个逻辑函数的卡诺图就是将此函数的最小项表达式中的各最小项相应地填入一个方格图内，此方格图称为卡诺图。卡诺图的构造特点使卡诺图具有一个重要性质：可以从图形上直观地找出相邻最小项。两个相邻最小项可以合并为一个与项并消去一个变量。

例如：给定一组待化简的逻辑函数F(A,B,C,D)=∑m(0,3,5,6,7,10,11,13,15)，其卡诺图化简过程为：

如图1（1）中所描述的是函数F中所对应的数值,其间标有“1方格”的项就是函数中各个数值在卡诺圈中的描述；而图1（2）中有五个卡诺圈,所描述的就是全部质蕴涵项；在图1（3）中标有带有“*”号的最小项为必要最小项，它们分别是最小项 m0，m3，m5，m6，m10，m13。由此可见,卡诺图上圈出的五个质蕴涵项均为必要质蕴涵项。最后的结果即为：F(A,B,C,D)=ABCD+ABC+ABC+BD+CD

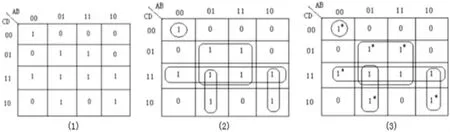
图1 函数F(A,B,C,D)的卡诺图化简流程图

由此可知卡诺图化简逻辑函数的一般步骤为：首先做出函数的卡诺图，然后在卡诺图上圈出函数的全部质蕴涵项，接着从全部质蕴涵项中找出所有必要质蕴涵项，最后若函数的所有必要质蕴涵项尚不能覆盖卡诺图上的所有“1方格”，则从剩余质蕴涵项中找出最简的所需质蕴涵项，使它和必要质蕴涵项一起构成函数的最小覆盖，即最简的质蕴涵项集。

2 系统运行(化简逻辑代数部分)流程图

图2 化简流程图

3 计算机实现逻辑代数化简的主要流程

3.1 十进制表示的最小项转换为二进制表示的最小项程序设计

在化简前将给定的逻辑代数表达式（一般为十进制数）转换为二进制数。用数组num[i]来接受输入的一组十进制数,然后由trans()函数实现十进制到二进制的转换，最后输出。

算法1：十进制转换为二进制算法

3.2 全部质蕴涵项程序设计

算法思想：逐个检查标1方格的合并方向,先圈没有或只有一个合并方向的标1小方格,后圈可能合并方向较少的标1小方格,最后圈那些可能合并方向较多的标1小方格,这样所得的卡诺圈都是质蕴涵项。即画卡诺圈时，先画大圈，再画小圈，而且大圈中不再有小圈。

在算法2中,Remainder[]存放待处理元素集,Rlength存放待处理元素集长度,Combination[]存放合并结果集,Clength存放合并集长度,notsingle标志有无相邻项。

算法2：化简算法

3.3 求必要质蕴涵项

将每个素蕴涵项中所包含的最小项求出。若某个素蕴涵项所包含的最小项至少有一个未被其它素蕴涵项包括,那么它就是实质素蕴涵项；若实质素蕴涵项集包含了所有标1小方格,那么它就为所求的最小覆盖,否则就需求最小覆盖。

3.4 求最小覆盖

最小覆盖就是要覆盖全部最小项，又要使质蕴涵项数目达到最少。这样必要质蕴涵项就是必须选用的质蕴涵项。最终化简的结果通常为最简与或表达式。

在覆盖所有最小项的前提下,卡诺圈的个数达到最少，每个卡诺圈达到最大。

4 实现计算机逻辑代数化简的实现重点

在用C++的描述中，多次涉及到数组，函数调用以及For循环的使用,因而必须有清晰的思路，才能得以程序的实现。要清晰的知道二进制数在转换过程中各个位的存储原理，以及多次循环赋值的描述，空间的申请与释放等。

逻辑代数化简过程中的实现：求“全部质蕴涵项程序的实现”是一难点.根据列表法的化简思想，必须将一组二进制数多次分组，多次循环对比，然后在对比的基础上找出这一组二进制数中有且仅有一位相异的，然后再进行相消合并处理。

5 结束语

利用计算机软件化简逻辑代数克服了代数法和卡诺图法以及列表法化简的不足,可适于多个变量的逻辑代数化简,而且对于化简结果不单一的逻辑表达式,可输出所有的化简结果。使用该方法化简逻辑代数结果准确、高效。

［1］王玉龙.数字逻辑[M].北京:高等教育出版社,1987.

［2］毛法尧.数字逻辑[M].武汉:华中科技大学出版社,1996.

［3］郭京蕾.软件法化简逻辑代数[J].武汉理工大学学报:信息与管理工程版,2003(03).