不确定性数据的聚类分析研究及应用

顾洪博，张继怀

(1.东北石油大学计算机与信息技术学院，黑龙江大庆163318;2.大庆市让胡路区政府，黑龙江大庆163712)

近年来，随着数据采集、处理技术深入，不确定性数据受到越来越多的重视。诸如经济、军事、金融等领域的应用中，数据的不确定性普遍存在且至关重要。传统的数据管理技术却无法有效管理不确定性数据，研发实用的不确定性数据管理技术是当今热点。不确定性数据来源[1]存在原始数据不准确;使用粗粒度数据集合，查询结果存在不确定性;隐私保护;缺失值。

聚类是按照某个特定标准把一个数据分割成不同的类或簇，使得类内相似性尽可能的大，同时类间的差异性也尽可能的大。也就是说，聚类后同一类别的数据尽可能的聚集在一起，而不同的数据尽量分离。聚类分析是进行数据分析、数据挖掘、模式识别等的重要研究内容之一。现有的聚类算法大致有[2]划分、密度、层次法等。

1 基于密度的不确定性聚类分析

基于密度的算法从数据对象的分布密度出发，把密度足够大的区域连接起来，从而可以发现任意形状的类。此类算法除了可以发现任意形状的类，还能够有效去除噪声。常见的基于密度的聚类算法有DBSCAN、OPTICS。在计算对象的距离时因为不确定性对象有概率属性，可能会影响对象间的距离。因此提出距离密度函数P(o，o')表示元组o和o＇间的距离密度函数，则o和o＇间的距离在(a，b)之间的概率和距离分布函数 P(a

由于DBSCAN聚类方法具有适用于各种形状簇、对噪声和离群点不敏感等优良特性，Kriegel提出FDBSCAN算法[3]。该算法在对对象的不确定区间进行离散化抽样计算后，再计算得到的核心对象概率和密度可达概率，若核心对象概率＞0.5，则该对象是核心对象，否则不是核心对象;若密度可达概率＞0.5，则是可达密度区。该算法能对任意形状的不确定性数据类聚类，并且不易受噪声干扰。但由于对移动对象的离散化抽样，使该算法的计算量较大，该算法需要用户确定输入参数，如ε，p。一般用户对参数的设置不够专业，并且该算法对参数值较敏感，参数值的小变化会导致大差异的聚类结果。

同年，Kriegel又提出了 FOPTICS 算法[4]。该算法首先要计算核心距离和可达距离。这是对FDBSCAN的扩展。许华杰提出采用不确定性数据索引技术、基于密度的不确定性数据概率聚类方法—PDBSCAN[5]。首先重新定义了对象的(ε，ρ)邻居，记为

式中ε－距离阀值;p－概率阀值;P(dis(oj，oi)≤ε≥p－oi和oj之间的距离小于ε的概率大于p。

该算法的特点:(1)对概率核心对象和概率密度可达的计算是利用两个不确定性对象之间的距离的最小值和最大值作为限定范围，并考虑不确定性在该范围上的概率分布。(2)算法在判断概率核心对象和概率密度可达时允许用户设置概率阀值p;(3)通过R树和概率阀值索引PTI提高计算效率。但算法中概率阀值p的选取对聚类结果有很大影响。另外，MBR的x－bound构造过程会受p的影响，对MBR的压缩就越精细，裁剪效果就更好。但是，相应地会增加R树节点保存xbound信息的存储代价。

2 基于划分的不确定性聚类分析

在确定性数据挖掘中，划分算法中最常用的是k－means算法。2005年，文献[6]提出基于k－means算法不确定性数据聚类分析 －UK－means算法。基本思想与k－means相似:各数据点将被距离最近的簇吸收。考虑在聚类过程中的不确定性，提出的目标函数是基于平方误差和的期望值最小的聚类算法E(SSE)—expected(sum of squared errors)。目标函数计算公式是

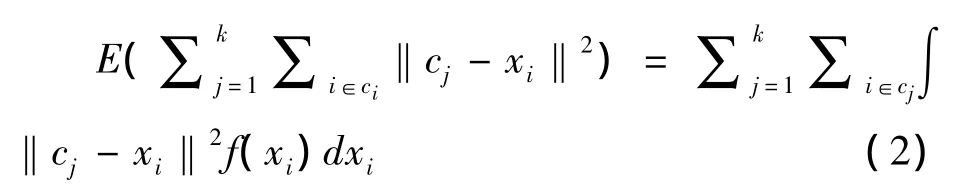
式中||.||－数据对象xi到簇中心ci的度量距离;f(xi)－数据对象xi的概率密度函数(pdf，probability density function)。

簇中心ci的计算公式为

作者认为UK－means算法和传统的K－means算法的最大差别是对算法中距离和簇的计算上。提出了一个基于移动对象的ED计算方法。在移动对象从(a，b)到(c，d)，质心为(p，q)。则

Ngai等在UK －means算法［7］中将 ED 表示成

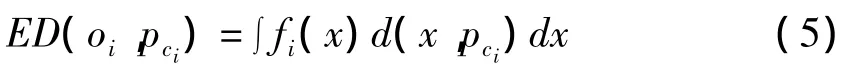
式中fi(x)－不确定性数据对象x的pdf;d(x，pci)－x与质心pi间的距离。

为了进行聚类，就要计算每一个数据对象的ED，计算量相当庞大，因此提出将数据点可能出现的区域用最小边界矩形(MBR)描述，通过MMD(min－max－dist，最小最大距离)设计剪枝策略:若 MinDistij＞，则 ED(oi，pi)不用计算，否则 ED(oi，pi)需要计算，其中 MinDistij是到簇质心pi的最小距离=min，ED(oi，pi))。此方法提高了计算效率。为了进一步计算，作者提出了4种方法来对范围进行估计，分别是 Ucs，Upre，Lcs，Lpre，这4种方法可以单独使用，也可以结合使用。但未给出具体的ED的计算函数或公式。

Cormode对前面的期望值进行实际计算[8]，提出采用一个函数来计算不确定的点到任意一个中心的距离的期望值，然后再运用传统的聚类方法进行计算。

基于划分的聚类分析算法，对于一个给定的n个数据对象的数据集，采用目标函数最小化的策略，通过把数据分成k个组，每个组为一个簇。可以看出，这种聚类算法适用于发现非凸面形状的簇，或者大小差别很大的簇。但它对于噪音和孤立点数据是敏感的。并且，对于初始聚类中心的选择会影响这类算法的执行效果。

3 实验及应用

3.1 基于密度的聚类分析实验

实验采用数据集来自美国地理信息基准数据集 SEQUOIA 2000[9]，p=0.8，比较的性能指标是聚类的准确度和效率。为了检验算法的效率，设对象的最大移动距离d=50 m，采用PDBSCAN和FDBSCAN聚类算法分别对具有不同移动对象数的数据集进行聚类。聚类相似度指标是Adjusted Rand Index(ARI)[10]，ARI 的值越大，说明两个聚类结果越相似，基于密度的聚类过程中ARI的值如表1所示。

表1 ARI与最大移动距离的关系Tab.1 The connection between adjusted rand index and the max－distance of mobile object

从表1中可看出，(1)PDBSCAN聚类算法的ARI高于FDBSCAN聚类算法。ARI的值与移动距离成反比。反之，当聚类中距离越小则移动对象的相似度越大，故ARI越大。(2)PDBSCAN算法的效率高于FDBSCAN算法。主要因为FDBSCAN算法首先要对数据不确定区域进行离散化，则需要时间较长和聚类过程较大;PDBSCAN算法通过R树索引和概率阀值索引预先对不满足要求的对象进行剔除，因此提高了聚类过程的效率。但PDBSCAN算法简便性较高于FDBSCAN算法。两种算法需要计算概率核心对象、概率密度可达和概率密度连续等数值。但前者是与0.5进行比较，后者是用户根据自己的聚类来设置阀值，故实验结果会与阀值有关。

3.2 基于划分的聚类实验

基于划分的聚类方法与基于密度的聚类算法不需要比较。在一个100×200D区域使用基于划分的聚类方法，n=1 000，k=20，目标函数平方误差和＜10－6。聚类相似度指标是ARI。算法采用的是文献[6]的算法。

表2 ARI与划分距离的关系Tab.2 The connection between adjusted rand index and the partition－based distance

从表2中可以看出，在不确定性数据中，ARI值与移动对象的移动距离有关。当对象间的距离越大，则聚类相似度就越小;反之，对象间的距离越小，则聚类相似度就越大。

3.3 在教学管理实际中的应用

在教学管理过程中，为准确掌握在校学生的成绩状况，常用问卷、测试、作业、老师或专家点评等方法。从这些方法整理出的数据是不完整的、模糊的、随机的、大量的，这里可以称为不确定性数据。教务管理者要从这些数据中挖掘有用的信息和知识，直观表征学生学习的总体状况，为教学和教学管理提供可靠依据。一般，以大学英语为例，数据来源于学生各个学期大学英语课堂表现10次、作业5次、模拟考试3次、期末考试成绩和各次参加大学英语四、六级的成绩。本文采用基于划分的不确定性数据聚类分析对教务管理中的数据进行分析，保证教学管理的准确性。此次实验中n=1 000，聚类簇数k=5，学生各次的成绩的变化我们成为移动距离，目标函数平方误差和p＜10－6，聚类相似度指标是 ARI。

表3 ARI与移动距离的关系Tab.3 The connection between adjusted rand index and the mobile distance－based

从表3中可以看出，在不确定性数据中，ARI的值与学生成绩的移动距离有关。当学生成绩的移动距离越大，则聚类相似度就越小;反之，学生成绩的移动距离越小，则聚类相似度就越大。并把算法在教学管理实际中的应用。

4 结束语

本文给出基于不确定性数据的聚类算法，分别就基于划分的和基于密度的聚类算法给出目前基本思想、优缺点，并就基于划分的和密度的算法进行对比实验，在教学管理实际中进行应用，可以为教学管理提供有力帮助。

[1]周傲英，金澈清，王国仁，等.不确定性数据管理技术研究综述[J].计算机学报.2009，32(1):1 －16.

[2]杨小兵.聚类分析中若干关键技术的研究[D].杭州:浙江大学计算机学院.2005.

[3]KRIEGEL H P，PFEIFLE M.Density－based clustering of uncertain data[C]//.Proceedings of the 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining.Chicago，2005:672－677

[4] KRIEGEL H P，PFEIFLE M.Hierarchical density －based clustering of uncertain data[C]//.Proceedings of 5th International Conference on Data Mining.Houston，2005:689－692.

[5]许华杰，李国徽，杨 兵，等.基于密度的不确定性数据概率聚类[J].计算机科学，2009，36(5):68－72.

[6]M CHAU R.CHENG B.KAO B，et al.Uncertain data mining:An example in clustering location data[C]//.In Pacific Asia Conferenceon Knowledge Discovery and Data Mining，2005:199 －204.

[7]NGAI W K，KAO B，CHUI C K，et al.Efficient clustering of uncertain data[C]//.Proceedings of the 6th International Conference on Data Mining.Hong Kong，2006:436－445.

[8] CORMODE G，MCGREGOR A.Approximation algorithms for clustering uncertain data[C]//.Proceedings of the 27th ACM SIGMOD－SIGACT－SIGART Symposium on Principles of Database Systems.Vancouver，2008:191－200.

[9]STONEBRAKER M，FREW J，GARDELS K，et al.The SEQUOIA 2000 Storage Benchmark[C]//.The 1993 ACM SIGMOD International Conference on Management of Data.Washington，1993:56 －98.

[10]YEUNG K，RUZZO W.An empirical study on principal componen analysis for clustering gene expression data[J].Bioinformatics，2001，17(9):763 －774.