双谱时延估计在被动测距中的应用

彭阐 姜可宇

（海军工程大学 武汉 430033）

0 引言 [1]

时延估计是被动测距声纳实现目标精确定位的关键。三元子阵声纳是目前潜艇装备使用的主要声纳，其工作原理是利用互相关法[1]测量目标辐射噪声到达各个阵元的时延信息来估计方位及距离。但其受海洋环境噪声的影响较大，时延估计精度不高。海洋环境噪声一般呈高斯分布，而双谱法时延估计在理论上能完全抑制高斯噪声，因此提出用双谱法时延估计代替互相关法来抑制海洋环境噪声对时延估计的影响。仿真结果表明相比于互相关法，双谱法时延估计精度更高，误差更小。

1 被动测距数学模型

假设目标是点源，声波按球面波方式传播。设等间距的三阵元 1、2、3，阵元间距为d，目标方位θ，目标到各阵元的距离分别为 r1、r2、r3。r2即要测定的目标距离r，如图1所示[2]。

图1 三元阵被动测距示模型

设在极坐标系中，目标的坐标为 S ( r,θ)，阵元坐标分别为1:(d,- π/2)，2:(0,0)，3:(d,π/2)，则目标到三个阵元的距离分别为（以 r2为参考）：

设声速为c，τ1、τ2、τ3分别表示声波到达三个阵元的时延，则时延差分别为:

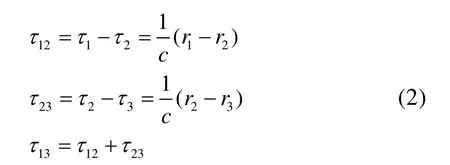
整理得到目标的方位和距离的表达式分别为

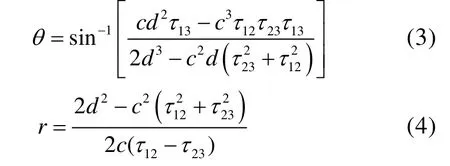
实现目标方位距离的精确测量的关键就是对τ12、τ23的精确估计。

2 双谱法时延估计的基本原理

假定三个空间分离的传感器，它们的测量数据 y1( n)、 y2( n)和 y3( n)满足下列方程：

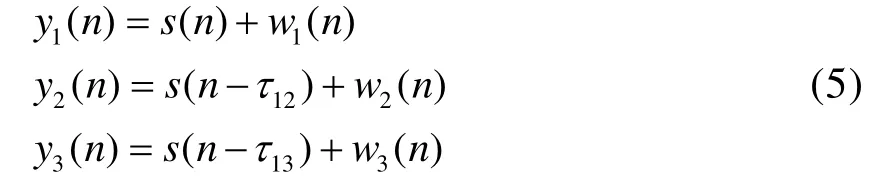
离散化处理后得：

搜索R12(τ)的最大值即可估计出时延差τˆ12，同理也可估计出时延差τˆ13，进而求解出τˆ23，代入式(3)、(4)解算出目标方位和距离。

在早期被动测距声纳的工程实现中，为了互相关硬件实现的需要，往往将接收信号进行 1bit量化[3]，进行极性相关，此时互相关函数定义为：

其中：

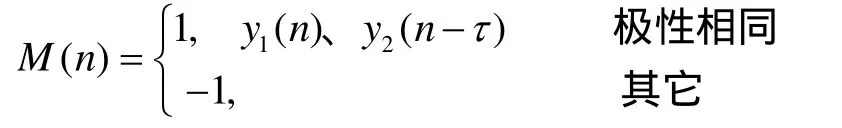
实际中背景干扰主要为高斯噪声，受硬件设备限制，信号和噪声的观测时间长度有限，信号和噪声、噪声与噪声的相关值并不等于 0，其中噪声间的相关是影响时延估计精度的主要因素。

Nikias C.L.等提出双谱时延估计法[4]，利用高斯噪声双谱理论值恒为零来抑制高斯噪声影响。以阵元1和2为例，它们的自双谱和互双谱为：

对其作傅里叶反变换得到：

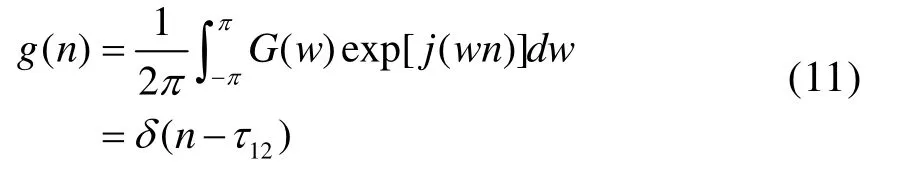
搜索g( n)的峰值即可估计出时延差τˆ12。同理可估计出时延差τˆ13，进而求解出τˆ23并解算出目标方位和距离。这就是双谱法时延估计的基本原理。

3 时延估计仿真

假设相邻阵元间隔为20 m，信号采样频率为10 kHz。在方位45°，距离3000 m处有一噪声目标。舰船辐射噪声在秒级别一般呈现非高斯性[5]，故设定目标辐射噪声为带限有色混合高斯噪声，混合高斯模型[6]为un为混合高斯序列的第 n个样本值，α为混合参数，设为 0.9， f1、 f2分别为高斯分布 N(0,1)和N(0,100)的PDF。频带为1600~4000 Hz，带内频谱为-6 dB/oct，如图2所示。设阵元接收噪声为高斯噪声且相互独立，功率谱与目标辐射噪声信号相同，如图3所示。

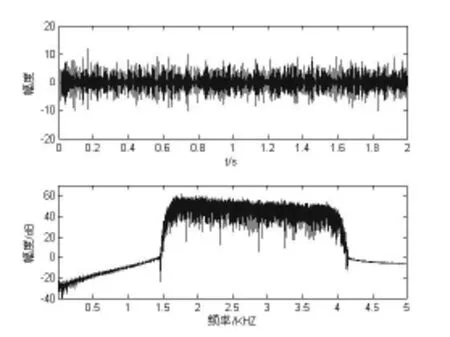
图2 目标辐射噪声及功率谱图

计算两个时延差τ12和τ13分别为95 ms和189 ms，经采样周期量化后为95和189。在距时延差真值最大偏差 20个采样周期的范围内计算互相关函数值。利用互相关法和双谱法估计时延差。

设定子阵信噪比为-15 dB到0 dB。在每一个信噪比下，利用互相关法和双谱法估计时延差，独立进行1000次仿真实验，比较两种方法在时延估计精度和估计方差上的差异。如图4～7所示。

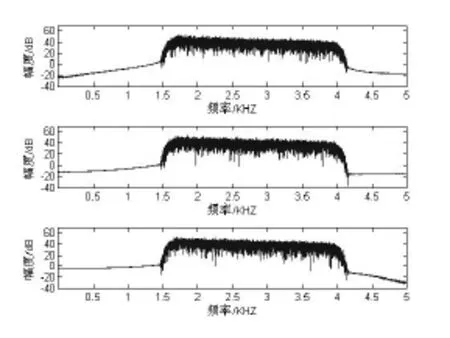
图3 背景噪声功率谱图

图4 τˆ12准确估计概率

图5 τˆ13准确估计概率

图6 τˆ12的估计根方差

图7 τˆ13的估计根方差

从仿真结果可以看出对τˆ12、τˆ13的准确估计概率上，信噪比-15 dB到-10 dB范围内，相对于互相关法，双谱法时延准确估计概率提高了30%-40%，估计根方差有2到7个采样周期的降低。

4 小结

本文从被动测距声纳工作的背景出发，通过仿真分析，比较了双谱法和互相关法在时延估计精度上的差异，结果表明，双谱法时延估计在信噪比-15 dB到-10 dB范围内，相对于互相关法，时延准确估计概率提高了30%-40%，估计根方差有2到7采样周期的降低。但双谱法在时延估计上所需计算量较大，时间也较长，在实际应用方面还需要论证和研究。

[1]Knapp C H, Carter G C.The generalized correlation method for estimation of time delay[J]. IEEE Trans.ASSP, 1976, 24(4): 1210-1218.

[2]李启虎. 声纳信号处理引论. 第二版. 北京: 海洋出版社, 2000: 334-340.

[3]宋新见. 数字式噪声目标被动测距声纳研究[D]. 哈尔滨: 哈尔滨工程大学, 2004.

[4]C.L.Nikias and R.Pan, “Time delay estimation in unknown Gaussian spatially correlated noise” , IEEE Trans. Acoust, Speech, Signal Processing, vol. 1988,36(11): 1706-1714.

[5]Brockett P L. Hinch M, Wilson G R. Nonlinear and Non-Gaussian Ocean Noise. JASA, 82(4)1987. 10.

[6]王平波, 蔡志明, 姜可宇. 混合高斯有色数据的生成方法研究. 声学与电子工程, 2007, 25(1): 7-12.