基于输入状态线性化的船舶航迹系统鲁棒控制及仿真

王震宇 吴汉松 吴瑶

（海军工程大学电气与信息工程学院，武汉430033）

0 引言

为了在最短的时间里到达目的地和减少燃油的消耗，总是力求使船舶以一定速度直线航行[1]。对船舶进行直线航迹控制具有非常强的针对性和实践性，也因此引起人们极大的关注，并很快成为当今船舶运动控制研究中的一个热点[2]。目前，随着海军现代化建设的需要，海军舰船的操控性直接影响到舰船的战斗力，实现舰船在各种干扰情况下的航迹跟踪，其意义非常重要[3]。

在通常意义下，鲁棒控制就是要试图描述被控对象模型的不确定性，并估计在某些特定界限下达到控制目标所留有的自由度。鲁棒控制一直是一个非常活跃且具有挑战性的研究领域。经历了众多学者二十几年的努力，鲁棒控制理论得到了长足的发展，并取得了令人瞩目的成果，逐渐形成了相对完整的理论体系[4-6]。闭环增益成形的控制算法是利用H∞控制的混合灵敏度控制算法的结果，用具有工程意义的参数直接构造出补灵敏度函数，其核心是直接用构造的系统闭环传递函数矩阵的表示式设计控制器，用于构造补灵敏度函数的四个参数：最大奇异值、带宽频率、关门斜率和闭环频谱峰值都是具有实际的工程意义。其理论的物理概念清晰，求解过程简单，故可以说闭环增益成形控制算法是一种工程意义简化的H∞鲁棒控制算法[7]。

本文将 H∞控制中的闭环增益成形鲁棒控制算法与输入状态精确反馈线性化相结合，针对船舶航迹系统的非线性数学模型，给出一种鲁棒控器的设计方法，在加入扰动后，控制该控制器也能有效使船舶行驶在预设航迹上，有效保证船舶航迹非线性系统的鲁棒稳定性和鲁棒性能。

1 船舶航迹控制系统数学模型

图1为船舶航迹控制示意图：

图1 船舶航迹控制坐标图

其中：x, y为船舶重心相对于坐标系XOY的坐标，ø为航向角，U为船舶前进速度。假定设定的直线航迹与X轴重合，则艏偏角就等于航向角ø，船舶直线航迹控制的非线性数学模型：

其中：r为艏摇角速度，δ为输入舵角，T, k, α为船舶操作性能参数[8]。船舶航迹控制的目标就是在全局范围内保证横偏位移y、艏偏角Ø和艏摇角速度r都趋近于零。

2 控制器的设计

在船舶运动控制非线性系统中：

向量场

显然rank(A)=3，矩阵A满足对合条件，所以系统(1)是可以输入—状态线性化的。

定义z=(z1z2z3)T，z1可由以下条件获得：

方程（3）最简单的解为 z1= y，则可以得到z2=Usin φ，z3=Ucosφ⋅r，得到的线性控制系统为：

通过状态变换和输入变换，利用原控制输入δ来镇定原非线性系统的问题已经转化为使用新控制输入v来镇定新系统的问题。

与该控制规律相对应的原控制输入为[8]：

在该系统中n=3，所以有：

采用Nomoto船舶模型：G=K/[s(Ts+1)]为被控对象，该模型被广泛应用与船舶自动舵的控制器设计中，用该模型设计出的控制器阶次较低易于实现，同时，补灵敏度函数T的奇异值曲线近似构造为奇异值为一的三阶惯性系统的频谱曲线T，利用基于闭环增益成形算法的控制器。

则有：

计算得：

控制量v为：

将式(6)、式(7)和式(8)代入式(5)可得新的控制律为：

3 仿真研究

针对某实习船进行仿真研究，参数如下[5]：船长126 m，船宽20.8 m，满载吃水为8.0 m，方形系数为0.681，航速V=7.7 m/s，通过计算得K=k=0.48，T=216，取α=30，T1=5。假设设定横偏位移y=200，艏偏角Ø =pi/18，输入舵角δ=0，利用本文提出的控制算法进行仿真。

在标称参数的情况下，其仿真结果如图2、图3和图4所示：

图2 标称参数下舵角的输出曲线

图3 标称参数下的横偏位移的输出曲线

图2、图3和图4表明，在无干扰的环境下，H∞控制中的闭环增益成形鲁棒控制算法与输入状态精确反馈线性化相结合得到的控制律能够使横偏位移y和艏偏角Ø很快收敛到零，舵角的变化较小，很快趋于稳定，具有较好的控制效果。

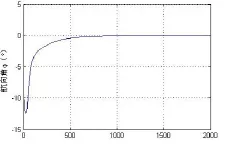
图4 标称参数下的航向角的输出曲线

下面对存在扰动的情况进行仿真。设计参数T1=5，取幅值为0.0155频率为0.3的正弦干扰加入到Ø，相当于风浪流扰动对船舶产生8°的等效舵角。

由图5、图6和图7可以看出，在风浪干扰下，该控制器也可以使控制对象较快趋向与合理的范围之内，操舵的频率和幅度都很小，偏航量和航向角都在很小幅度内变化。该鲁棒控制器对船舶的航迹跟踪有较好的控制效果，具有很好的鲁棒稳定性。

图5 扰动下舵角的输出曲线

图6 扰动下横偏位移的输出曲线

图7 扰动下航向角的输出曲线

4 结束语

本文针对船舶直线航迹控制系统的非线性数学模型，将H∞控制中的闭环增益成形鲁棒控制算法与输入状态精确反馈线性化相结合，得到一个新的反馈控制规律，能够使系统能够较快趋于稳定。

以某货船为对象，在Matlab/Simulink环境下进行仿真研究，仿真结果表明，由H∞控制中的闭环增益成形鲁棒控制算法与输入状态精确反馈线性化相结合的控制规律可以使船舶直线航迹控制全局渐进稳定，具有较好的稳定性，对存在干扰的情况下也能够使横偏位移y和艏偏角Ø收敛到零，且鲁棒性较好，设计的控制律具有比较理想的控制效果。

[1]彭秀艳, 李小军, 沈艳, 赵希人. 大型船舶航迹多变量随机最优控制[J]. 船舶工程, 2003, 25(3): 41-45.

[2]李铁山, 杨盐生, 洪碧光. 船舶直线航迹控制的鲁棒自适应非线性设计[J]. 大连海事大学学报, 2003,30(4): 1-5.

[3]DO K D,JIANG Z P, PAN J. Robust global stabilization of under actuated ships on linear course:state and output feedback [J], Int. J. Control, 2003, 76(1): 11-17.

[4]Kharitonov V.L.Asymptotic stability of an equilibrium position of a family of systems of linear differential equations [J]. Differential Uarvneniyu,1978, 14: 2086-2088.

[5]Zames G. Feedback and optimal sensitivity: model reference transformations, multiplicative seminorms,and approximate inverses. IEEE Trans. Automat,Contr.1981, 26(2): 303-32.

[6]Doyel J C. Analysis of control systems with structured uncertainty. IEEE Proc. Part D.1982, 129: 242-250.

[7]贾欣乐, 张显库. 船舶运动智能控制与H∞鲁棒控制[M]. 大连: 大连海事大学出版社, 2002: 273-277.

[8]周岗, 姚琼荟, 陈永冰, 周永余, 李文魁. 不完全驱动船舶直线航迹控制稳定性研究. 自动化学报[J],2007, 33(4): 379-383.

[9]Jean-Jacques E. Slotine, Weiping Li. Applied Nonlinear control[M]. 北京: 机械工业出版社.