逆转变异蚁群算法在CGF多目标分配中的应用

张 媛， 张立民， 刘文彪， 陈 洁

(海军航空工程学院，a.4系;b.7系;c.3系，山东 烟台 264001)

0 引言

目标选择属于组合优化的NP问题，其目的是通过目标排序，确定目标的优先级，将优化目标分配给各友机，以便各CGF(Computer Generated Forces)实体采取有针对性的应对措施。虚拟空战仿真中的目标分配是许多CGF作战飞机行为决策的基础，它模拟的准确性直接影响其他CGF实体行为和实体模拟的真实性。

近年来，在多机协同目标分配决策仿真中，文献［1－5］采用遗传算法解决最优目标的分配问题。虽然遗传算法能够在可行时间内得到较大问题规模的满意解，但是其交叉算子的合适选择是十分困难的，而且还存在着所谓的“基因漂移”现象，从而使算法容易陷入局部最优。随着蚁群算法在解决离散组合优化问题方面的良好性能体现［6］，黄树采首先将基本蚁群算法应用于防空C3I系统的目标分配问题研究中［7］，随后文献［8－11］根据各自仿真要求对基本蚁群算法进行了改进，实现了超视距空战条件下协同空战的目标分配问题。但是蚁群算法收敛速度一般比较慢并且易于陷入局部最优状态［12］的缺点仍没有很好地得到解决。

受文献［13］中对预警机指挥引导下多机协同空战目标选择方案的优化求解启发，本文将遗传算法的逆转变异算子融入蚁群算法中，对蚁群算法问题解空间搜索策略以及信息素强度更新规则进行改进和设计，提高了CGF实体指挥决策过程中目标选择方案的搜索效率。

1 多机协同目标选择问题描述

假定有m架蓝方战机与n架红方战机进行空战，在预警机指挥引导下，空中指挥员已获得红蓝双方的飞行态势。根据文献［14］中关于超视距协同空战整体威胁态势的计算方法，建立蓝机Bj对红机Ri(j=1，2，…，m)的态势优势矩阵 s=［sij］，i=1，2，…，n，j=1，2，…，m，目标分配的最优解指标取分配战机打击全部目标的优势函数最大。取决策变量xij，xij表示第i个火力单元(战机平台)是否打击第j个来袭目标，有

根据文献［13，15－17］建立目标分配优化函数表达式为

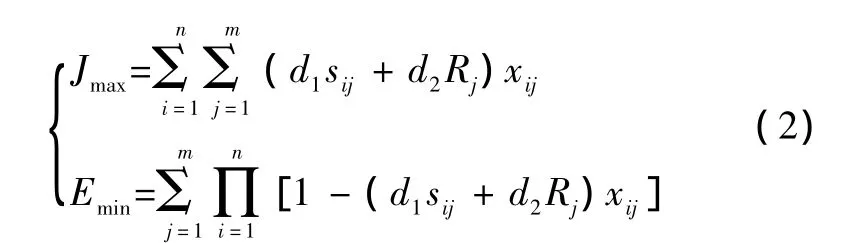
式中:J表示一轮具体目标分配后分配红方编队飞机迎击全部目标的最小不利因素函数;sij为红方第i架飞机对蓝方第j架飞机的综合态势优势函数值;Rj表示第j架蓝机的战役价值;d1和d2为加权系数，根据作战任务的不同而定。如要进行要地防空任务时，取d1=0.4，d2=0.6;纯空空格斗时可选取 d1=1，d2=0;对于蓝方战机数大于红方战机最大攻击能力时，选取d1=0.6，d2=0.4。

2 目标优化选择模型设计

蚁群算法是意大利学者Macro Dorigo最早在国际上提出的［18］，并用该算法求解TSP等问题，取得了较好的效果。应用蚁群算法求解协同目标分配问题，根据协同目标分配的特点，对蚁群算法进行如下改进:

1)将分配红方战机打击全部蓝方目标的优势函数最大作为最优解指标;

2)红方每攻击一架蓝方飞机后，应对原来的态势优势函数矩阵进行修正;

3)信息素强度采用全局修正规则进行信息更新;

4)借鉴遗传算法的变异操作思路，当蚁群算法中目标分配的优化解在一次循环内没有明显改进时，可对此时获得的解进行逆转变异操作，可以提高目标分配的全局策略。

2.1 目标分配策略

为了避免目标分配在搜索的一开始就以较大的概率集中于局部几个优势函数较大的目标上，进而失去目标解的多样性，改进算法中设置一个信息量刺激阈值p0，只有当信息量的刺激趋于阈值p0时，蚂蚁才在信息量的刺激下趋于信息量较大的路径，以获取多样性的解，将分配的目标放入目标分配矢量π中，π=(T1，T2，…，Tm)。π(i)=Tj表示红方第 i架飞机攻击蓝方目标 Tj，Tj∈R，j=1，2，…，m。那么处在目标节点r的第k只蚂蚁依据方程(3)可选择所要转移的目标单元节点j为

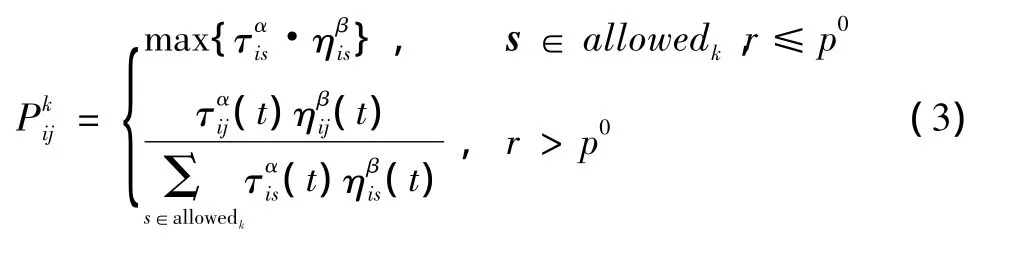
式中:p0∈(0，1);r是(0，1)中均匀分布的随机数;τij是节点i和j之间的信息素强度;ηij是蚂蚁搜索时的启发信息值，取启发式信息值ηij=d1sij+d2Rj;α≥0是轨迹的相对重要性;β≥0是蚂蚁搜索时的启发式信息值。

由上式可知，蚂蚁在选择路径时尽可能选择目标综合优势大而且信息素强度趋于阈值p0的方向，在一定程度上削弱了蚁群陷入局部最优的趋势。

2.2 信息量的全局修正

随着进化时间的推移，以前留下的信息逐渐消逝，用参数(1－ρ)表示信息消逝程度，经过n个时刻，蚂蚁完成一次循环，信息素强度全局更新规则表示为

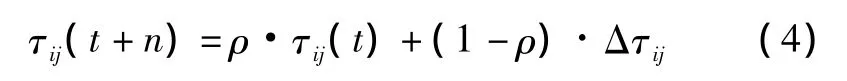
其中，

式中:Δτij=表示第k只蚂蚁发现本次循环中的最短路径;Q为比例系数，影响算法的收敛速度;Ek表示第k只蚂蚁在本次循环中获得的红方飞机打击蓝方飞机的不利因素函数值。

通过式(4)可以看出，只有构成全局最优路径的边才有机会增加信息素水平，其他边的信息素则由于挥发作用逐渐降低而使搜索的目的性大大增强。

2.3 引入逆转变异方式

为了克服蚁群算法计算时间较长的缺陷，借鉴遗传算法的变异操作思路，当蚁群算法获得的目标选择优化解在一次循环内没有明显改进时，则对该最优解进行逆转变异操作，可以提高目标选择的全局搜索能力，明显改善整体的性能。

逆转变异操作是从一次循环中的最优解个体中随机挑选两个逆转点，再将两个逆转点间的基因交换，逆转变异过程表示为变异前A'取2 4 1 3 5 7，变异后A″取2 5 1 3 4 7。

定义逆转变异条件为

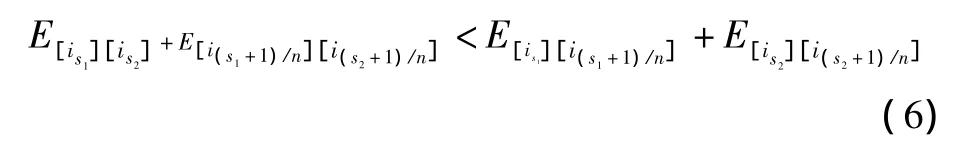
其中:i0i1i2…i(n－1)，(i0，i1，i2，…，i(n－1)∈{0，1，2，…，n －1})表示某个个体所走路径。s1，s2∈{0，1，2，…，n－1}，符号“/”表示整除符号。进行操作 inversion(s1，s2，solutioni)，函数 inversion()的功能是把个体solutioni的s1+1和s2这一段路径颠倒过来进行变异，变异的次数是随机的。这一过程涉及的运算比蚁群算法中的循环过程要简单得多，因此只需要较短的时间便可完成相同次数的运算。经过这种变异算子作用后，这一代解的性能会明显改善，也大大改善了整个群体的性能，从而减少计算时间，提高搜索效率。

2.4 仿真步骤

基于变异蚁群算法求解协同目标选择步骤分7步实现:

1)nc←0(nc为迭代步数或搜索次数)，给τij(i=1，2，…，n;j=1，2，…，m)矩阵赋相同的数值，给出 Q，ρ的值;

2)将S只蚂蚁随机放在S个初始目标节点上;3)对每个蚂蚁按转移概率Pkij选择下一个节点;

4)计算本次分配的不利函数的和E，比较出最好的结果(E最小)，并记录此次循环中最好结果的最优路径;

5)根据式(6)进行最优解空间的逆转变异条件判断，若变异后路径长度小于变异前，就保留这次最优分配方案，否则维持原值;

6)按更新方程(4)修改信息强度，nc←nc+1;

7)若nc大于规定的循环次数，记录当前蚂蚁的位置(当前的解)，停止运行，输出最好的解，否则转第3)步。

3 算法实验

假设红方有8架A型截击机A1～A8(各带1枚可迎头攻击的某型中程空空导弹:射程为75 km，使用高度22000 m，Ma数为4)，使用高度22000 m。蓝方参战飞机为两架B型(B1、B2)和两架 C型(C3、C4)战机(各带两枚可全向攻击的某两型远程空空导弹，射程分别为70 km和80 km，使用高度分别为18000 m和20000 m，Ma数均为3)，使用高度为18000 m。蓝机的机型为F－16D和F－15E，其雷达最大跟踪距离分别为130 km和140 km。红机的雷达最大跟踪距离Ri=120 km。在某一时刻红方机群坐标为A1(－30 km，190 km，10 km)，A2(20 km，200 km，12 km)，A3(－20 km，190 km，10 km)，A4(20 km，200 km，12 km)。蓝方机群坐标为 B1(－42 km，260 km，7 km)、B2(10 km，276 km，11 km)、C3(－20 km，265 km，10 km)、C4(30 km，270 km，10 km)，将上述参数带入文献［14］关于超视距协同空战整体优势态势的计算公式中，计算出超视距协同空战态势数据，如表1所示。

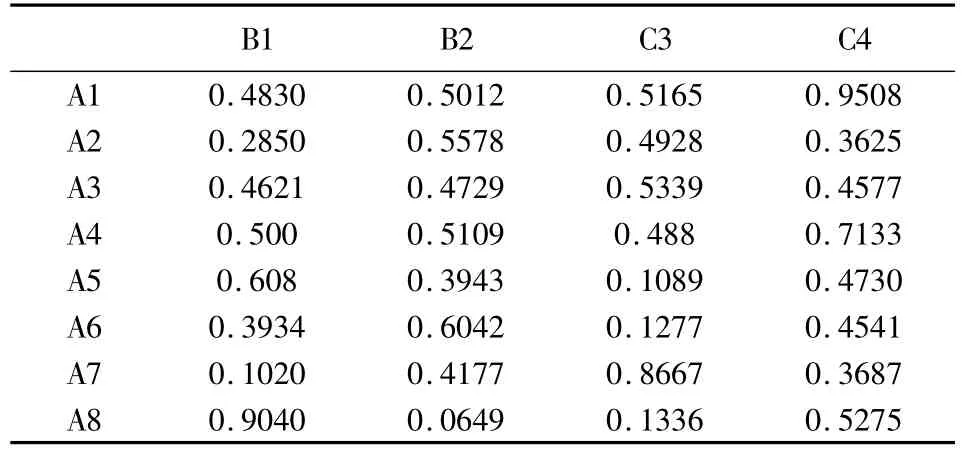
表1 态势矩阵Table 1 The situation matrix

根据文献［14］中关于总体态势威胁评估函数的定义，由表1可知，A7对B1的优势最小，优势值为0.1021，故红方应派出相应的飞机对B1进行攻击;同理可得，B2对A5，C3对A6以及C4对A2均具有很大的威胁。因此，为避免红方兵力的歼灭，预警机应采取相应的目标分配方案来引导红方战机进行空战。

设置蓝方飞机4个目标的战役价值向量R为(0.8，0.8，0.6，1.0)，按照参数的最优选择原则［19］，经反复参数设置实验，目标分配RAACA算法参数设置为 Q=1000，α =0.1，β =1.5，ρ=0.1，p0=0.8，利用Matlab在相同条件下对本例进行仿真，得出目标分配运算结果π，如式(7)和表2所示。

求得最优解时，E=0.2636，J=6.0032。

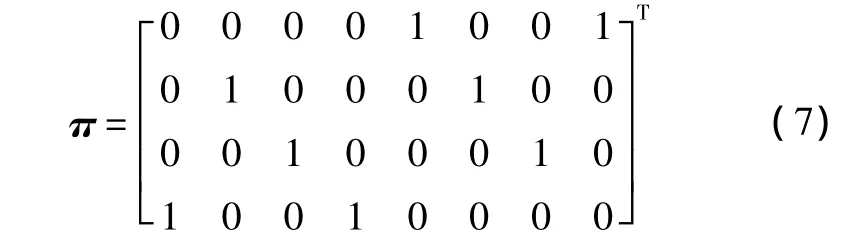
表2 目标分配优化方案Table 2 The optimal method for the target assignment

为了进一步验证RAACA算法在多机协同空战仿真中目标选择问题的效果，在相同的仿真环境下分别采用RAACA算法和基本蚁群算法对该实例各进行10次仿真实验，每次迭代运算均为100代终止。

在实验中，RAACA算法均能在循环30代以内获得最优解，而采取基本蚁群算法最好情况需循环70代左右才能获得最优解。两种算法的最优结果比较如图1所示，其中RAACA表示逆转变异蚁群算法，ACA表示基本蚁群算法。

图1 最佳实验结果比较Fig.1 Comparison of the optimum experimental results

4 结论

由仿真实验结果表明，基于变异的蚁群算法能够有效解决预警机指挥引导下的多机协同空战仿真中的目标选择决策问题。该方法在蚁群算法中引入遗传算法的逆转变异算子对目标选择构造策略进行更新，并且改进和设计了信息素强度的更新规则，提高了空战仿真中目标选择方案的搜索效率，能够在较短的迭代次数内获得最优的目标选择方案，很好地体现了现代空战仿真中CGF实体目标选择的实时性和真实性。

［1］刘付显，邢清华.基于混合遗传算法的目标优化分配［J］.系统工程理论与实践，2002，30(7):84-88.

［2］LEE Z J，SU S F，LEE C Y.Efficiently solving general weapon-target assignment problem by genetic algorithms with greedy eugenics［J］.IEEE Transactions on Systems，Man，and Cybernetics，2003，33(1):113-121.

［3］冯杰.遗传算法及其在导弹火力分配上的应用［J］.火力与指挥控制，2004，29(2):43-46.

［4］LUO Delin，SHEN Chunlin，WANG Biao，et al.Air combat decision-making for cooperative multiple target attack:An approach of hybrid adaptive genetic algorithm［J］.Journal of the Graduate School of the Chinese Academy of Sciences，2006，23(3):382-388.

［5］罗德林，吴顺祥，段海滨，等.无人机协同多目标攻击空战决策研究［J］.系统仿真学报，2008，20(24):677-678.

［6］柳长安，李为吉，王和平.基于蚁群算法的无人机航路规划［J］.空军工程大学学报:自然科学版，2004，5(2):9-12.

［7］黄树采，李为民.目标分配问题的蚁群算法研究［J］.系统工程与电子技术，2005，27(1):79-80.

［8］罗德林，段海滨，吴顺详，等.基于启发式蚁群算法的协同多目标攻击空战决策研究［J］.航空学报，2006，23(6):1166-1170.

［9］GAO S.Solving weapon-target assignment problem by a new ant colony algorithm［C］∥Proceedings of the 6th World Congress on Intelligent Control and Automation.2008:221-224.

［10］于雷，任波，鲁艺.自适应蚁群算法的多机协同空战目标分配方法［J］.火力与指挥控制，2008，33(6):49-51.

［11］陈中起，张斌，任波.随机优化蚁群算法在空战决策中的应用［J］.电光与控制，2008，15(6):54-57.

［12］GAMBARDELLA L M，DORIGOM.Ant-Q:A reinforcement learning approach to the traveling salesman problem［C］//Proceedings of the 12th International Conference on MachineLearning，1995:252-260.

［13］赵磊，李仁松，常国任.预警机引导战斗机空战目标分配模型［J］.指挥控制与仿真，2008，30(5):34-36.

［14］滕鹏，刘栋，张斌，等.超视距协同空战态势评估方法研究［J］.电光与控制，2008，15(10):47-50.

［15］付新华，王健.多机协同多目标攻击的目标分配和攻击排序［J］.火力与指挥控制，2006，31(3):75-78.

［16］高坚，佟明安.超视距多目标攻击排序及火力分配建模与解算［J］.火力与指挥控制，2004，29(3):9-12.

［17］李永宾，张凤鸣，李俊涛.多机协同攻击决策逻辑的蚁群算法研究［J］.电光与控制，2006，13(6):43-45.

［18］DORIGO M，MANIEZZO V，COLORNI A.The ant system:Optimization by a colony of cooperating agents［J］.IEEE Trans.on Systems，Man and Cybernetics，Part-B，1996，26(1):1-13.

［19］詹士昌，徐婕，吴俊.蚁群算法中有关算法参数的最优选择［J］.科技通报，2003，19(1):381-186.