控制受限影响下不确定时滞系统的滑模控制

贾廷纲，牛玉刚，夏 康

(1. 华东理工大学 信息科学与工程学院，上海 200237；2.上海电气集团股份有限公司 中央研究院，上海 200070)

0 引言

由于信道带宽和网络拥塞等环境因素的影响，实际物理系统中广泛存在着时滞现象，而时滞（包括状态时滞和输入时滞）常常会导致控制系统性能变坏，甚至失稳。因此，时滞系统的控制一直是研究的热点问题，而且，近年来关于时滞系统的滑模控制问题也开始受到关注(见参考文献[1]～[4])。

众所周知，滑模控制突出特点是对参数摄动和外部干扰具有较强的不敏感性。作为一种有效的鲁棒控制方法，滑模控制在机械手控制、电机驱动等领域取得了广泛应用（见参考文献[5]～[7]）。值得注意的是，上述研究工作都假设系统的控制输入不受任何限制。

然而，现实物理系统中一些不可避免的限制存在常常导致激励端呈现非线性特征：饱和、死区、回环、继电特性等。这些非线性输入会导致系统性能下降，最终使得整个控制系统不稳定。因此，近年来对于控制输入受限系统的研究受到了许多研究者的关注，特别是， 基于滑模控制技术的输入受限控制系统的研究工作也取得了一些有意义的研究成果(见参考文献[8]～[10])，但是。对于同时存在状态时滞和输入时滞情况下，输入受限系统的滑模控制问题尚未取得有效的研究进展，而且，上述一些已有的研究工作并不能简单地被推广到此类问题。

基于上述分析，本文将研究输入受限情况下不确定时滞系统的滑模控制问题，其中，被控系统存在状态时滞和输入时滞，同时，参数不确定性同时存在系统参数矩阵和控制输入矩阵中。本文选择了一种新的积分型滑模面，并证明了所设计的滑模控制律能保证系统状态轨迹在有限时间内到达该切换面，同时，利用Lyapunov方法和线性矩阵不等式（LMI）技术，给出了闭环系统渐近稳定的充分条件。

1 系统描述

考虑下面的不确定输入时滞系统：

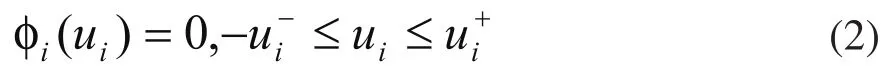
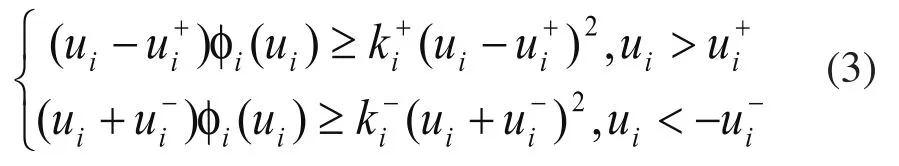
不失一般性，假设：

1）B列满秩，(A，B）可控；

本文的控制目标是设计滑模控制律，以保证被控制系统(1)是全局渐近稳定的。

下面的引理将在后面的证明中用到。

引理1 设E，H，F(t)为适当维数的实矩阵，且F(t)满足FT(t)F(t)≤I，则对于任意非零常数ε＞0有：

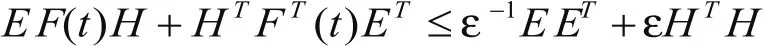
引理2 设X，Y为适当维数的实矩阵，对于任意非零常数ε＞0有：

2 滑模面的设计与滑模性能分析

本节将首先设计滑模面，并通过Lyapunov方法和线性矩阵不等式（LMI）技术，给出了滑模动态渐近稳定的充分条件。本文选择切换函数为：

其中，辅助变量 满足以下条件：

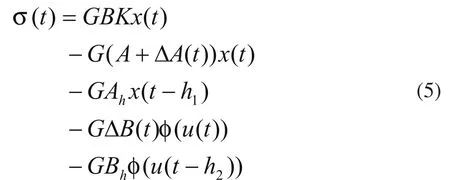
其中，设计矩阵G∈Rm×n满足GB为非奇异矩阵，常数矩阵K∈Rm×n满足A-BK是Hurwitz矩阵。由矩阵理论可知，由于B为列满秩，如果选择G=BTX（其中X＞0将在后面的设计中给出）能保证矩阵GB非奇异。

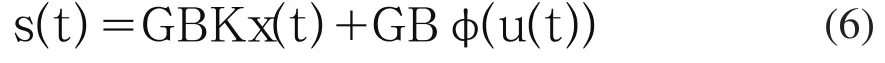
利用 ，可以得到等效控制律为：

将式(7)代入系统(1)，可以得到切换面s(t)=0上的滑模动态方程为：

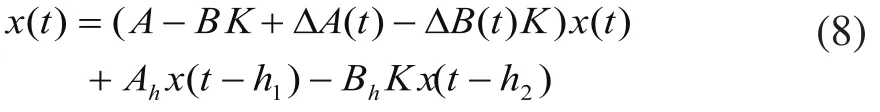
定理 1 考虑不确定时滞控制系统（1）和条件(2)、(3)，选择由式(4)、(5)确定的切换面s(t)=0。如果存在正定矩阵X＞0，R1＞0，R2＞0和标量ε1＞0，ε2＞0满足线性矩阵不等式：

其中，

且滑模矩阵为G=BTX, 那么滑模动态（7）是全局渐近稳定的。

证明：

选取Lyapunov函数为

沿滑模动态（8）的状态轨迹对V(t)求导，得到：

根据引理1，对于任意非零常数ε1＞0有：

由ΔB(t)=Bδ(t)及根据引理2，对于任意非零常数ε2＞0有：

将式（11），（12）代人式（10）得：

其中

3 控制律的设计

作为滑模控制设计的第二步骤，下面将设计滑模控制律保证系统状态轨迹能在有限时间到达滑模面s(t)=0，并被吸引在该滑模面上。

由于系统（1）的控制输入满足非线性限制条件(2)、(3)，因此，本文设计如下的滑模控制律：

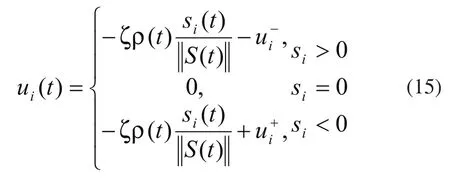
下面定理将证明，虽然系统(1)存在不确定性及控制输入受限，但所设计的滑模控制律（15）仍就能够保证所设计的切换面的可达性。

定理2 考虑不确定时滞控制系统（1），满足假设条件（2）～（3）。如果切换面由（4）、（5）确定，其中G=BTX（X＞0满足线性矩阵不等式（9），则滑模控制律（15）可以保证系统状态轨迹在有限时间内被吸引到由所确定的切换面s(t)=0上。

证明：由（15）可得，当Si＞0时因此，由（3）及（15）可知：

当Si＞0时，

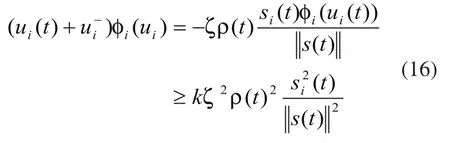
当Si＜0时，

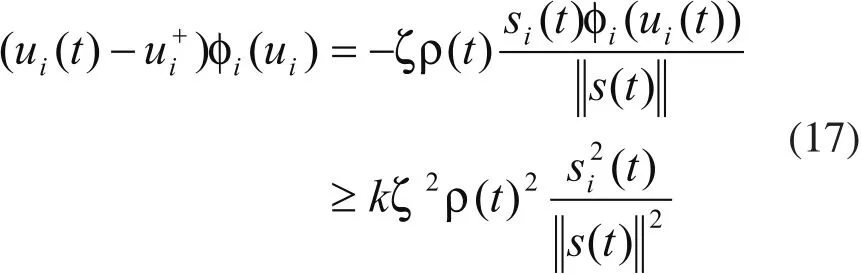
由（16）-（17）式，可得对于所有si有：

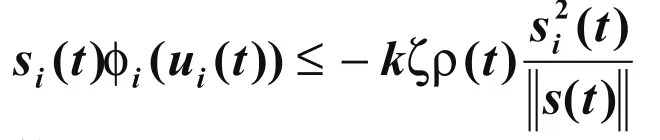
从而：

从而，由（6）、（18）式可知：

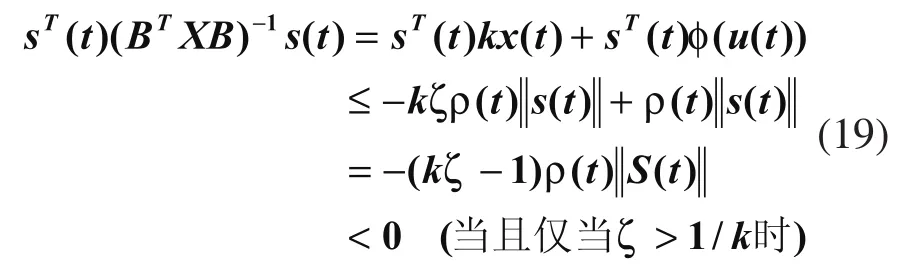
这表示对于由（4）、（5）式所确定的滑模面的可达性条件成立。证毕。

文中控制器输入端的非线性表示具有一定的普遍性，设计的滑模面有一定的灵活性，保证了系统状态轨迹的最终稳定性，独特的控制律设计也保证了可达性的成立。

4 结论本文研究控制输入受限情况下时滞系统的滑模控制，给出了切换函数和滑模控制律的设计方法，

分析了闭环系统的稳定性；并且已在磨煤机、表格轮转印刷机、压缩机的智能控制系统中应用，在下一步的研究工作中，我们将进一步将本文方法应用于其它机电设备的驱动控制系统中。

[1] Y.Niu and Daniel W C Ho. Robust observer design for Ito stochastic time-delay systems.Systems&Control Letters,2006,55:781-793.

[2] Y.J.Huang and H.K.Way.Sliding mode control design for discrete multivariable systems with time-delayed input signals, Int. J.of Systems Science,2002,33:789-798.

[3] M.Yan and Y.Shi.Robust discrete-time sliding mode control for uncertain systems with time-varying state delay.IET Control Theory&Applications,2008,2:662-674。

[4] F.Da.Sliding mode predictive control for long delay time systems[J].Physics Letters A,2006,348(3):228-232。

[5] 孙宜标,郭庆鼎,等.基于模糊自学习的交流直线伺服系统滑模变结构控制[J].电工技术学报,2001,16(1):52-56.

[6] 吴勃,许文芳,陈虹丽.神经滑模控制在机器人轨迹跟踪中的应用[J].电机与控制学报.2009,13(A01):99-104.

[7] 李丽霞,宛波,田卫华.滑模变结构控制在直流直线电机中的应用研究[J].沈阳工程学院学报(自然科学版),2010,6(7):35-37.

[8] 陶洪峰,胡寿松.具有饱和死区非线性输入的自适应滑模跟踪控制.信息与控制.2009,38(3):281–285.

[9] Y.Niu and D.W.C.Ho.Design of sliding mode control for nonlinear stochastic systems subject to actuator nonlinearity联[J].IEE Proc.-Control Theory Apply,2006,153(6):737–744.

[10]胡庆雷,马广富.带有输入非线性的挠性航天器姿态机动变结构控制.宇航学报[J].2006,27(4):630–634.