一种机织物增强柔性复合材料拉伸性能加载速度依赖性的试验研究*
2012-07-02汪泽幸蒋金华陈南梁
汪泽幸 蒋金华 陈南梁
(1.湖南工程学院纺织服装学院,湘潭,411104;2.产业用纺织品教育部工程研究中心,上海,201620;3.东华大学纺织学院,上海,201620)
近年来,织物增强柔性复合材料在建筑膜结构、柔性充气结构、柔性储液罐、轻型输送带等领域的应用越来越多。织物增强柔性复合材料在使用过程中主要依靠外加张力保持外形,且抗拉不抗压,因此,对该复合材料的拉伸性能进行研究十分必要。
目前,对织物增强柔性复合材料拉伸性能的研究,多对其在特定加载速度下的力学性能进行测试与分析。在对聚合物基复合材料的压缩瞬时[1]、拉伸有限元分析[2]时,通常认为聚合物基复合材料的变形特性与应变率无关。但国内外众多学者研究发现,聚合物[3]及其复合材料[4-10]的力学性能具有一定的应变率依赖性,同时在不同加载速度下的拉伸曲线也有一定的差别,即认为高分子及其复合材料的拉伸特性具有应变率敏感性或应变率依赖性。这主要是由于高分子及其复合材料具有黏弹性,在拉伸过程中强迫高弹性形变过程和断裂过程都是松弛过程,时间因素的影响很大,因而作用力的速度也直接影响着强迫高弹形变的发生和发展。对于相同的外力来说,加载速度过快,强迫高弹形变来不及发生,或者强迫高弹形变得不到充分的发展,试样发生脆性断裂;加载速度过慢,则线型玻璃态高聚物会发生一部分黏性流动。只有在适当的加载速度下,玻璃态高聚物的强迫高弹性才能充分地表现出来[9],因此只有在同一加载速度下测量的结果才具有可比性。
从现有的文献来看,对全塑性材料的应变率依赖性的研究较为深入,并对其应变率敏感性指数进行了理论计算[11],而对具有高黏弹性的织物增强柔性复合材料的加载速度依赖性研究较少。吴明全等[12]对ETFE薄膜力学性能对加载速度的依赖性进行了试验研究,张营营等[13]考察了单向拉伸条件下,PTFE膜结构材料抗拉强度和断裂应变随着加载速度的变化情况,为膜结构材料力学特性的深入研究及其工程应用提供了基础性数据。
本文以用于制备轻型输送带的机织物增强柔性复合材料为研究对象,对其在不同加载速度下的抗拉强度、断裂应变、屈服强度及失稳应变随加载速度的变化趋势进行了分析。
1 材料选用与试验方法
1.1 试验材料
本文选用的柔性复合材料以涤纶机织平纹织物为增强骨架材料,单面涂覆PVC制备而成,其整体结构及增强骨架材料结构示意图如图1所示。其中,涤纶机织物以111.11 tex超低收缩聚酯长丝为经纱,以直径为0.3 mm聚酯单丝为纬纱,织物密度为6.7根/cm×3.5根/cm。成品柔性复合材料的面密度为230 g/mm2,厚度为2.24 mm。
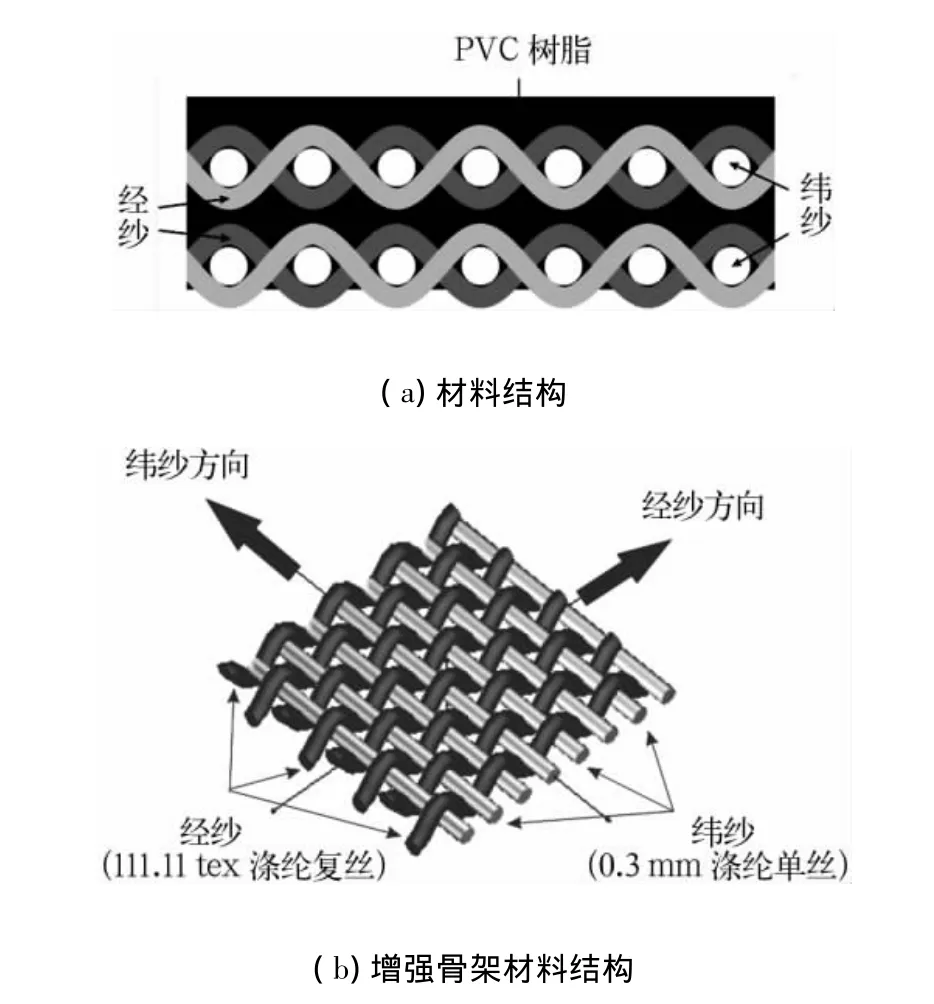
图1 试验材料的结构示意图
1.2 试样规格与测试方法
为减少拉伸过程中试样与夹头内表面间的滑移及试样在夹头附近断裂,除试样两端夹持部位采用铝片保护外,还采用了非矩形试样,以进一步减少试样滑移。本文选用的试样规格及尺寸见图2。

图2 试样外形及尺寸示意图
因选用的机织物增强柔性复合材料用于制备轻型输送带,在使用过程中主要承受纵向(经纱方向)拉伸载荷作用,故仅对纵向试样进行测试与分析。所有拉伸试验均在WDW-20型万能材料试验机上进行,受到拉断试验时间和试验机所能允许的加载速度因素的影响,加载速度分别选用5、50、100、150、200 和 300 mm/min,即对应的名义应变速率分别为 2.5、25、50、75、100 和 150%/min。由载荷传感器记录加载载荷,位移传感器记录试样对应的位移,并基于拉伸曲线获得拉伸性能指标,对拉伸性能指标随加载速度的变化趋势进行分析。
所有试验均在室温下进行。
2 拉伸性能指标
2.1 抗拉强度与断裂伸长率
机织物增强柔性复合材料在外加载荷作用下拉伸至断裂时,会产生较大的变形,当外加载荷达到最大值时发生断裂。其表现为拉伸应力—应变曲线无下降阶段,最大抗拉强度Sb对应的应变为断裂应变εb,如图3所示。由于拉伸过程中很难测得试样宽度和厚度的变化,因此本文不考虑拉伸过程中试样宽度的缩小,仍然采用拉伸前试样的宽度来计算应力。在弹性阶段,织物增强柔性复合材料的应变量较小,试样宽度变化较小;而在断裂前,试样延伸率较大,此时试样宽度变化相对较大,因此本文得到的织物增强柔性复合材料的抗拉强度小于实际应力。
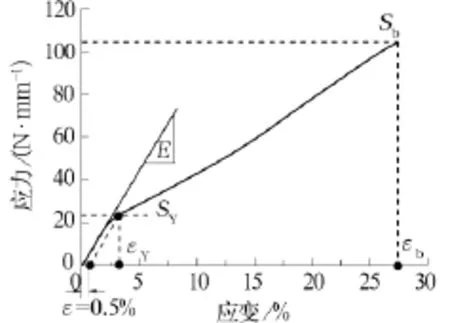
图3 拉伸性能指标确定示意图
2.2 拉伸弹性模量
织物增强柔性复合材料的拉伸弹性模量E采用拉伸曲线初始近似直线段的斜率来表示,见图3。
2.3 屈服强度与失稳应变
织物增强柔性复合材料无明显的屈服极限,在拉伸曲线上表现为无明显的屈服点。对于这类材料通常采用残余变形法来确定其屈服强度,本文采用以产生0.5%塑性应变时的应力作为屈服强度,如图3所示。该屈服强度通常称为条件屈服强度SY,对应的应变称为失稳应变εY,见图3。
3 试验结果与分析
3.1 拉伸响应曲线
图4为6种加载速度下的应力—应变曲线(1~5为测试号)。从图中可以看出,不同加载速度下的应力—应变曲线形状具有很好的相似性,表明机织物增强柔性复合材料在不同加载速度下具有相同的变形和破坏机理。在断裂前,均经历较大的变形过程,且无明显的下降阶段;在小应变条件下,同等加载速度下的拉伸曲线间分散性较小。随着加载应变的增加,拉伸曲线之间的分散性逐渐显现。
3.2 抗拉强度及断裂伸长率与名义应变率的关系
由图5可见,随着加载速度的提高,机织物增强柔性复合材料的抗拉强度增加,而断裂伸长率有所降低,在性能上表现为脆性增加。随着加载速度的提高,材料性能的分散性也有所增加。
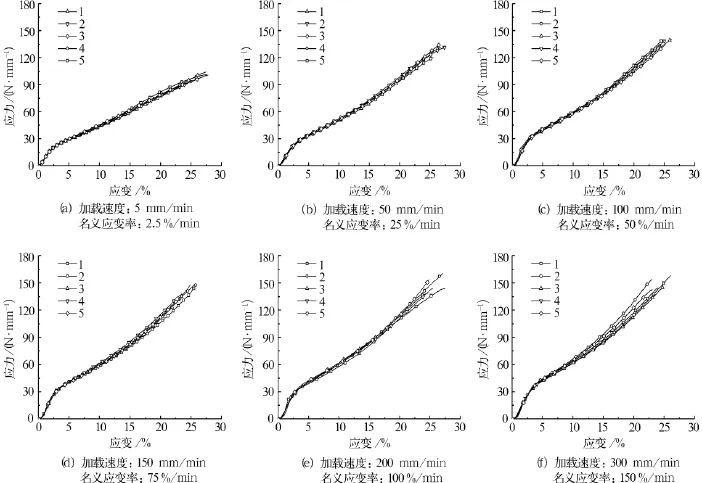
图4 不同加载速度下的拉伸曲线
从图5中可以发现,抗拉强度(Su)和断裂伸长率(εu)与名义应变率()的对数间具有很好的线性关系,这个关系可用式(1)和式(2)来描述:
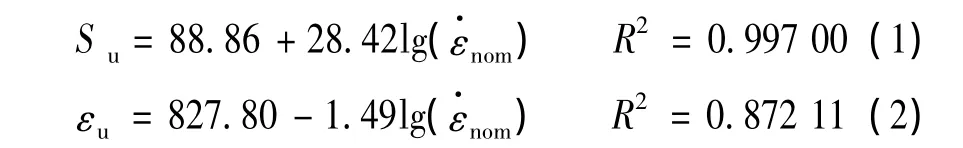
从拟合直线的斜率绝对值来看,加载速度对抗拉强度的影响程度较大,而对断裂伸长率的影响程度相对较小。
3.3 拉伸弹性模量与名义应变率的关系
图6表明,机织物增强柔性复合材料的拉伸弹性模量E随名义应变率的增加而增加,同时弹性模量间的离散程度增加。当名义应变率)从2.5%/min增加到150%/min时,拉伸弹性模量增加了55.45%,且拉伸弹性模量的CV值从0.67%增加到6.23%。
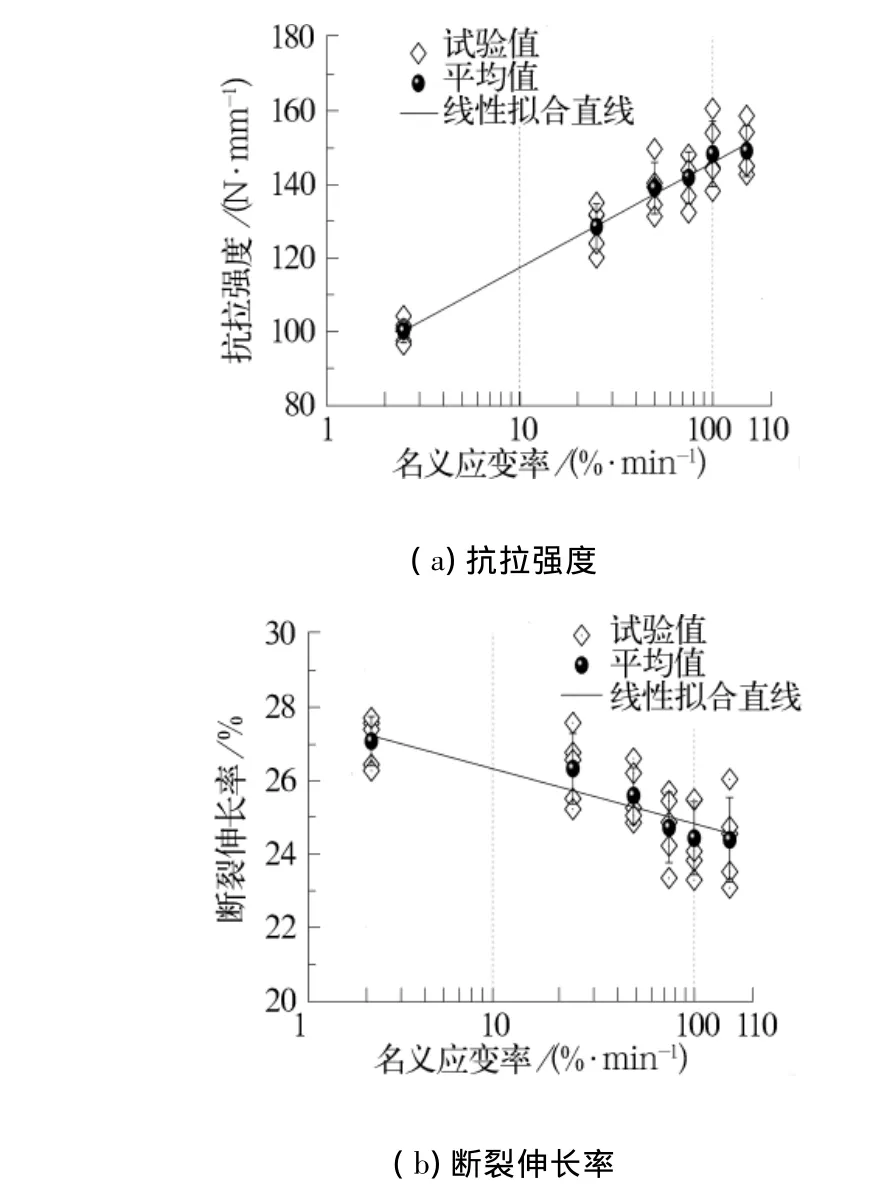
图5 抗拉强度及断裂伸长率与名义应变率之间的变化关系

图6 拉伸模量与名义应变率之间的变化关系
弹性模量E随名义应变率的变化趋势可用式(3)来表示:
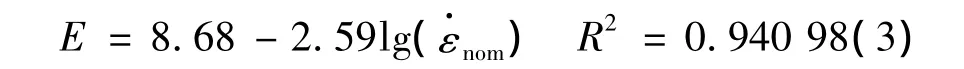
3.4 屈服强度及失稳应变与名义应变率的关系
图7表明,随着名义应变率ε·nom的增加,屈服强度和失稳应变均呈现增加的趋势,其中屈服强度的增加程度相对较大。当名义应变率ε·nom从2.5%/min增加到150%/min时,屈服强度增加了55.66%,而失稳应变增加了17.86%。
屈服强度和失稳应变随名义应变率的变化趋势可用式(4)和式(5)来表示:
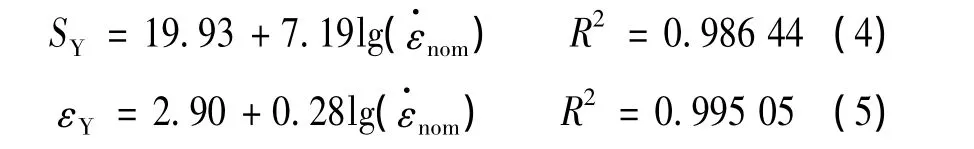
从拟合直线斜率的角度而言,加载速度对屈服强度的影响程度较大,而对失稳应变的影响程度相对较小。
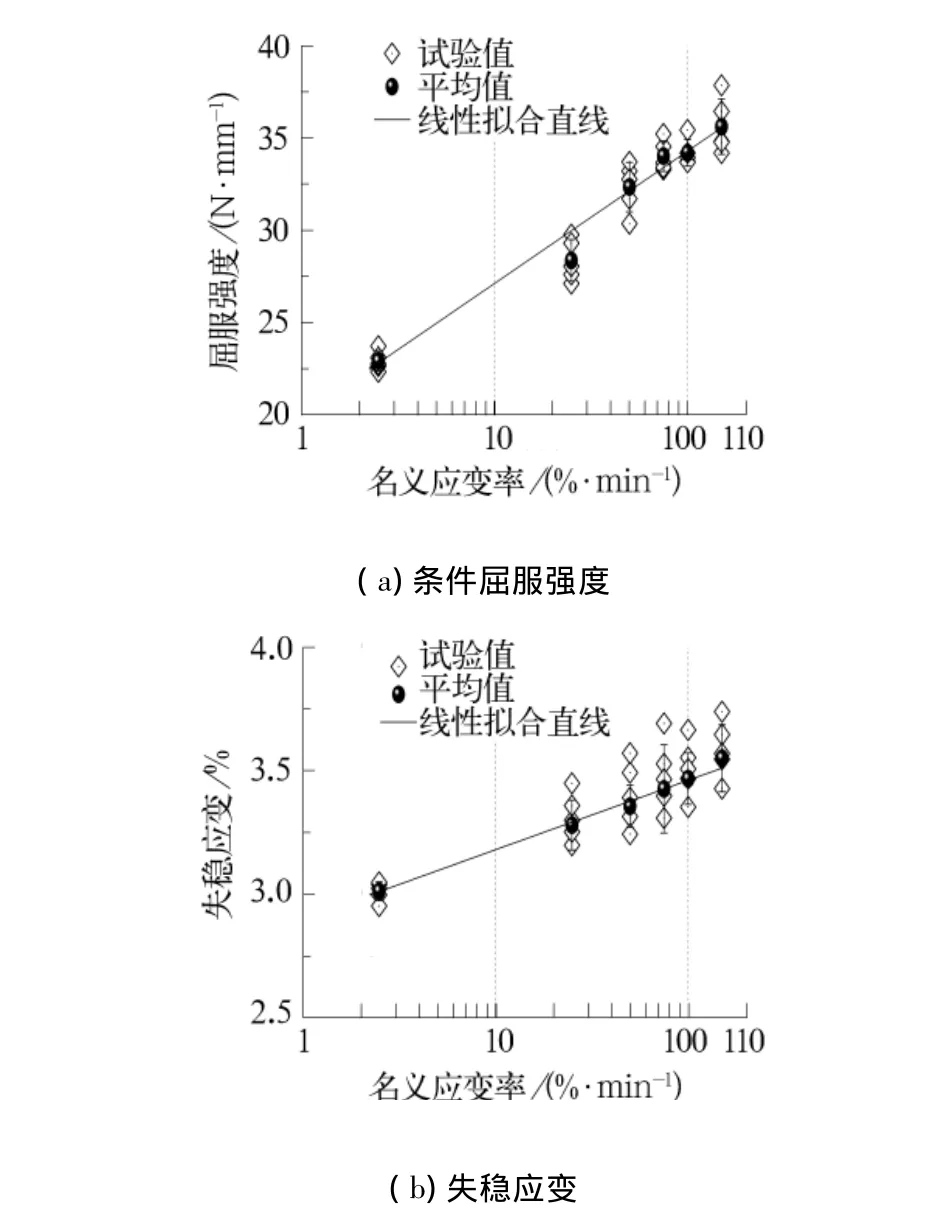
图7 屈服强度及失稳应变与名义应变率之间的变化关系
4 结语
本文以用于制备轻型输送带的机织物增强柔性复合材料为研究对象,对其在不同加载速度下的拉伸性能指标进行了测试,并对抗拉强度、断裂伸长率、拉伸弹性模量、屈服强度与失稳应变随加载速度(名义应变率)的变化趋势进行了分析和讨论。试验和分析结果表明,机织物增强柔性复合材料具有明显的加载速度依赖性或应变率相关性;在不同加载速度下,机织物增强柔性复合材料的应力—应变曲线变化趋势具有很好的相似性,表明在不同加载速度下这种复合材料的变形机理相似,且抗拉强度、拉伸弹性模量、屈服强度和失稳应变均随着加载速度的提高而增加,而断裂伸长率有所下降。
受试验设备等因素的影响,本文采用的加载速度范围为5~300 mm/min,加载速度范围较窄。为进一步研究织物增强柔性复合材料在较宽加载速度范围内抗拉性能的变化趋势,有必要对其加载速度敏感性做进一步研究,并对不同加载速度下织物增强柔性复合材料的本构方程、加载速度敏感性的量化等做深入的试验研究和理论分析。
[1] HAMOUDA A M S,HASHMI M S J.Testing of composite materials at high rates of strain:Advances and challenges[J].Journal of Materials Processing Technology,1998,77:327-336.
[2] 龙海如.纬编针织物增强复合材料力学性能研究[D].上海:东华大学,2002.
[3] BROWN R.Handbook of polymer testing:Short term mechanical tests[M].United Kingdom:Rapra Technology Limited,2002.
[4] HSIAO H M,DANIEL I M.Strain rate behavior of composite materials[J].Composites Part B,1998,29(5):521-533.
[5] SHIM V P W,LIM C T,FOO K J.Dynamic mechanical properties of fabric armour[J].International Journal of Impact Engineering,2001,25(1):1-15.
[6] AKIL Ö,YILDIRIM U G,DEN M,et al.Effect of strain rate on the compression behavior of a woven fabric s2-glass fiber reinforced vinyl ester composite[J].Polymer Testing,2003,22(8):883-887.
[7] JADHAV A.High strain rate properties of polymer matrix composites[D].India:University of Pune,2003.
[8] TATSUOKA F I M,DI B H,KUWANO R.Time dependent shear deformation characteristics of geomaterials and their simulation[J].Journal of the Japanese Geotechnical Society of Soils and Foundations,2002,42(2):103-129.
[9] 宋孝浜,王春霞.纤维增强复合材料应变率效应研究进展[J].广西纺织科技,2006,35(4):31-34.
[10]王正浩,赵桂平,马君峰,等.碳/环氧树脂复合材料应变率效应的实验研究[J].复合材料学报,2007,24(2):114-119.
[11]宋玉泉,程永春,王习文.拉伸变形应变硬化指数的实验测量及其精细分析[J].中国科学:E辑,2001,31(3):193-203.
[12]吴明全,慕仝,刘建明.拉伸速度对ETFE薄膜力学性能的影响[J].建筑科学材料,2008,11(5):574-579.
[13]张营营,张其林,周传志.PTFE膜材料的单向拉伸性能[J].建筑材料学报,2010,13(4):535-539.
