Mohr－Coulomb内切圆屈服准则在ABAQUS软件边坡分析中的应用

伍韵莹，王志鹏，孙立宇

（1.广东省水利电力勘测设计研究院，广州510635；2.中国市政工程西北设计研究院深圳分院，广东 深圳518048；3.长春工程学院水利与环境工程学院，长春130021）

0 引言

鉴于边坡稳定性问题涉及到工程中的许多领域，近年来边坡分析方法也越来越多，特别是随着岩土材料的弹塑性有限元计算技术的发展，应用有限元法分析边坡稳定性得到了普遍推广。

目前，强度折减弹塑性有限元法是在边坡稳定分析中适用广泛、前景良好的一种数值分析方法。它是将强度折减技术与弹塑性有限元方法相结合，对边坡的稳定性进行分析，求得边坡的最小稳定安全系数。但是，影响计算结果计算精度的因素很多，除了有限元法引入的误差外，还依赖于所选用的屈服准则；同时，在通常的有限元分析程序中，材料参数是需要事先给定，为了得到边坡的最小稳定安全系数，需要多次修改给定值，计算量大，即使采用二分法一般也需要试算多次。

对于岩土材料来说，与其他屈服准则相比，Mohr－Coulomb屈服准则（简称 M－C准则）应用最广、时间最长；但是，M－C屈服准则假定材料的破坏与中主应力无关，而且在主应力空间的π平面上屈服面是一个等边不等角的六边形，屈服面存在尖角，在数值计算中收敛性较差，计算困难；Drucker－Prager屈服准则（简称D－P准则）在π平面上的屈服面不存在尖角，在数值计算中收敛性较好，但是需要采用合适的参数，否则计算精度较低，可能造成计算的边坡最小稳定安全系数较大。

基于此，本文采用ABAQUS软件中扩展的DP模型，结合 M－C内切圆屈服准则参数，并使用ABAQUS软件中的场变量对材料强度参数进行连续折减，整个分析过程一次完成，既大大减少了计算工作量，也为边坡的稳定性分析提供较为精确的结果。

1 数值分析方法

ABAQUS软件中提供了扩展的D－P模型，扩展的D－P模型的屈服面在π平面上不是圆形，屈服面在子午面上包括线性模型、双曲线模型和指数模型。扩展的D－P模型可以模拟土、岩石等摩擦材料在单调加载下的材料特性，同时也可以考虑材料的剪胀性。

经典的D－P模型的屈服准则的表达式如下：

式中：I1—— 应力张量的第一不变量；

J2——应力偏量的第二不变量。

α、k与材料参数相关。

在关联流动法则下推导平面应变状态时与MC准则匹配的D－P准则，即可得到M－C内切圆屈服准则（简称 DP1）的参数关系如下［1－2］：

式中：c、θ——M－C 准则中材料的凝聚力和内摩擦角。

本文采用 ABAQUS软件中线性的D－P模型［3］，屈服准则的表达式如下：

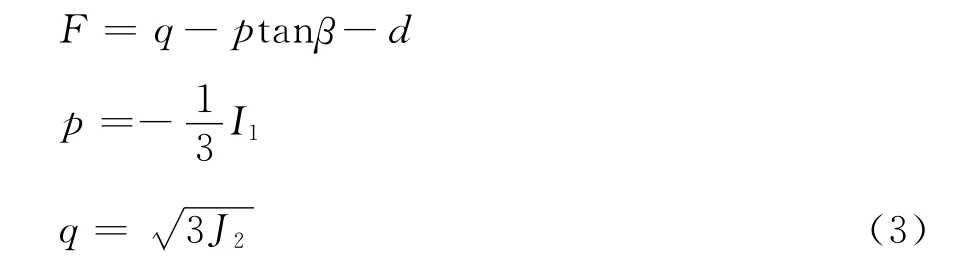
式中：β——材料的摩擦角；

d——材料的凝聚力，其值与输入的硬化参数有关，可以分别进行计算。

当硬化参数由单轴压缩试验参数σc（屈服应力）定义时：

当硬化参数由单轴拉伸试验参数σt（屈服应力）定义时：

式中：K——三轴拉伸与压缩屈服应力之比。

联立式（1）～ 式（4）可得：

式（6）即为ABAQUS软件中在关联流动法则平面应变状态时的参数转换式。

在ABAQUS软件中，所谓的场变量只是一个中间量，材料参数可以定义为场变量的函数，以便在问题的分析过程中对模型中各部分乃至全部区域进行参数的调整。例如温度场是其中最简单的一个场变量，此温度场只是一个变量场，不代表真实温度，只起到带动材料参数变化的作用，计算原理详见文献［4］。

抗剪强度折减系数的概念是由Zienkiewicz等［5］1975年在土工弹塑性有限元数值分析一文中首次提出的，由此所确定的强度储备安全系数与Bishop［6］在极限平衡法中所给的稳定安全系数在概念上是一致的。边坡的安全系数定义为把强度参数减小到边坡临界破坏时的强度参数折减系数，强度参数如下式进行折减：

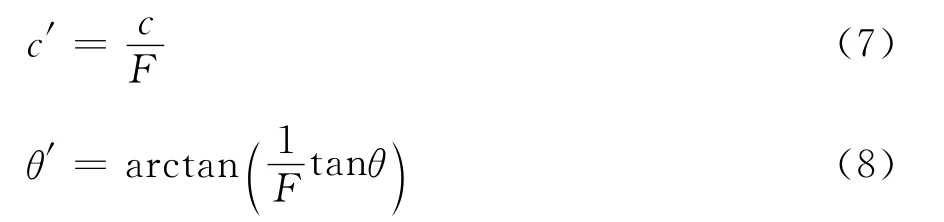
弹性模量E、泊松比μ在计算中假设为定值，不随c、θ值的改变而变化。

2 失稳判据

采用强度折减有限元法分析边坡稳定性的一个关键问题就是如何根据有限元计算结果来判别边坡是否处于整体破坏状态。目前，边坡失稳破坏的判据主要有以下几点［7］。

2.1 数值收敛判据

根据有限元解的收敛性确定失稳状态，即在给定的非线性迭代次数极限值条件下，最大位移或不平衡力的残差值不能满足所要求的收敛条件，则认为边坡在所给定的强度折减系数下失稳破坏。

2.2 位移判据

根据计算域内某一部位的位移与折减系数之间关系曲线的变化特征确定失稳状态，如当折减系数增大到某一特定值时，某一部位位移突然迅速增大，则认为边坡发生失稳。

2.3 塑性区判据

通过域内广义剪应变等某些物理量的变化和分布来判断，如当域内的塑性区（或某一幅值的广义剪应变）连通时，则判断边坡发生破坏。理论上，边坡的变形过程总是伴随着一些物理量的出现和发展，如塑性区、塑性应变、广义剪应变和应力水平等，当这些物理量达到一定的值时，边坡失稳。

本文主要针对位移判据和塑性区判据这两种判据进行分析，数值收敛判据仅起辅助效果，进行简单阐述。

3 算例分析

为了便于讨论，这里选用赵尚毅等［8－9］所采用的算例边坡作为计算对象，如图1所示。选用与文献［8－9］相同的计算参数，坡高H＝20m，坡角β＝45°，土的重度γ＝20kN／m3。对于土体，采用服从M－C屈服准则与关联流动法则的理想弹塑性本构模型以及服从DP1准则与关联流动法则的理想弹塑性本构模型进行计算，土的黏聚力与内摩擦角分别为c＝42kPa和θ＝17°。这里假定弹性模量E＝100MPa，泊松比v＝0.3。

边坡两侧为水平约束边界，底部为完全固定边界。采用四节点四边形单元进行剖分，如图1所示（X轴以水平向右为正，Y轴以竖直向上为正），有限元计算模型共含有1 062个节点和986个单元。

图1 计算模型／m

在重力荷载作用下，随着土体强度的折减，边坡内特征点的位移变化和塑性应变发展的最终情况如图2、3所示。

图2 特征点位移变化曲线图

从图2中可以看出，M－C准则与DP1准则两者计算结果基本上是一致的；但是DP1准则计算时，数值的收敛性较好，能够计算到边坡失稳的工况，而且还能够继续计算下去，此时数值收敛判据失真，采用位移判据进行分析，在F＝1.23时位移曲线出现了明显的转折点，可以认为其最小安全系数为1.23；M－C准则的数值收敛性不好，得到的位移曲线没有出现明显的转折点，位移已经基本上不再变化，很大程度上是迫于数值的不收敛，此时得到的最小安全系数也为1.23，与DP1的计算结果是相同的。

图3中PEEQ表示的是边坡在整个变形过程中塑性应变的累积结果。根据本文所建议的塑性应变与塑性区发展的失稳判据，随着土体强度参数的不断折减，土体塑性区发展区域逐渐增大。对于M－C准则来说，当F＝1.23时，边坡塑性区基本贯通，坡脚塑性应变已达3.67%。对于DP1准则来说，当F＝1.23时，边坡塑性区基本贯通，坡脚塑性应变已达2.00%。当F＝1.24时，塑性区基本贯通至坡顶，边坡已经失稳，认为其最小安全系数均为1.23。从上述计算结果来看，2个材料模型在采用不同的失稳判据得到的计算结果基本一致。

图3 边坡塑性应变最终分布图

4 结语

（1）在平面应变问题中，采用DP1准则进行模拟计算，能得到很好的结果，克服了M－C准则在数值分析时存在的不足，减少了数值计算的困难，在一定程度上，避免了收敛性的问题，同时充分吸取了M－C准则在描述岩土强度特性时的有效性，完全可以在岩土工程中获得广泛的应用。

（2）在ABAQUS中采用场变量进行强度参数的折减，能起到很好的效果，不需要每算一次改一次土体强度参数，大大减少了计算工作量，而且所得计算结果合理，表明了该方法的可行性。

（3）当采用位移判据时应选取多个位移特征点，以避免在位移变化曲线上找不到明显的转折点。

（4）当采用强度折减弹塑性有限元法进行计算分析时，数值收敛判据在应用上存在局限性，不具有广泛的适用性，尽管位移判据和塑性区判据在计算过程中也受到很多因素的影响，但是这些因素不足以改变边坡破坏的本质趋势，可以联合采用位移判据和塑性区判据来对边坡的失稳进行分析，以便得到更合理适用的结果。

［1］邓楚键，何国杰，郑颖人.基于 M－C准则的D－P系列准则在岩土工程中的应用研究［J］.岩土工程学报，2006，28（6）：735－739.

［2］张艳山，潘玉珍.基于ABAQUS对系列准则的讨论［J］.水电能源科学，2010，28（11）：70－72.

［3］苏凯，伍鹤皋，李冲.Mohr—Coulomb等面积圆屈服准则在围岩稳定分析中的应［J］.中国农村水利水电，2008，11：81－86.

［4］姚燕稚，陈国兴.基于场变量控制强度参数折减的有限元边坡稳定分析［J］.湖南大学学报，2008，35（11）：124－129.

［5］Zienkiewicz O C，Humpheson C，Lewis R W.A ssoci－ated and non－associated visco－plasticity and plasticity in soil mechanics［J］.Geostechnique，1975，25（4）：671－689.

［6］Bishop A W.The use of the slip circle in the stability analysis of slopes［J］.Geostechnique，1955（5）：7－17.

［7］张阳阳，李宗坤，李艳.基于ABAQUS的强度折减法边坡失稳判据研究［J］.浙江水利水电专科学校学报，2009，21（1）：13－15.

［8］赵尚毅，郑颖人，张玉芳.极限分析有限元法讲座—Ⅱ有限元强度折减法中边坡失稳的判据探讨［J］.岩土力学，2005，26（2）：332－336.

［9］刘金龙，栾茂田，赵少飞，等.关于强度折减有限元法中边坡失 稳 判 据的 讨 论 ［J］.岩 土 力 学，2005，26（8）：1345－1348.