GLBest-PSO算法在热工过程模型参数辨识中的应用

郝 超，徐志成

(常州机电职业技术学院，江苏 常州213164)

1 引言

随着现代火力发电机组越来越向着大容量、多参数发展，热工过程自动控制在大型火电机组中的地位越来越重要。要定量、准确地分析设计热工过程控制系统，一定要建立被控对象的数学模型。传递函数是描述热工对象数学模型的一种方法，获得对象传递函数的方法有阶跃响应法、最小二乘法、极大似然法以及基于神经网络、遗传算法(Genetic Algorithm，GA)等智能算法［1-4］。但是，很多算法由于对输入信号有一定的要求或算法过于复杂，一直很难在实际中实施。

粒子群优化 (Particle Swarm Optimization，PSO)算法［5］由Kennedy等人于1995年提出，已经被证明是一种很好的优化方法。其概念简单、实现容易，已成为当前智能计算领域的研究热点之一。Eberhart等［6］通过对速度项引入惯性权重 w，并在进化过程中动态调整惯性权重以平衡收敛的全局性和收敛速度，得到了标准 PSO算法。Clerc［7］在进化方程中引入收缩因子来进一步增强算法的收敛性，同时可以放松对速度的限制。针对算法特点，很多学者还提出了其他一些改进的版本。其中，M.Senthil Arumugam提出了一种全局-局部参数最优粒子群优化(Global-Local Best PSO，GLBest-PSO)算法，增加了粒子的多样性，避免算法过早收敛，提高了算法搜索效率。本文将该算法应用于热工过程的模型建立中，进行了初步的应用研究。

2 基于全局-局部参数最优粒子群优化算法

2.1 标准PSO算法

PSO算法是一种新型的演化计算方法，其基本原理为［5-6］:D维空间中存在 m个粒子，每个粒子的坐标为 xi=(xi1，xi2，…，xiD)，并且具有与优化目标函数f(x)相关的适应度，同时每个粒子具有各自的速度 vi=(vi1，vi2，…，viD)。对于第 i个粒子，其历史最好位置为 pi=(pi1，pi2，…，piD)，记为 pbesti;记群体中所有粒子经过的最好位置为 pg=(gi1，gi2，…，giD)，记为gbesti。对第 t代的第 i个粒子，粒子群算法根据式(1)计算第t+1代的第j维的速度和位置。

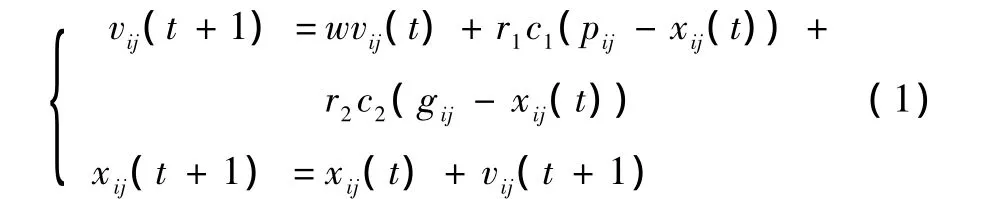
式中，w为惯性权重，它使微粒保持运动惯性，使其具有扩展搜索空间的趋势，有助于新区域的搜索;r1、r2为［0，1］的随机数;c1和 c2为加速度常数，表示将每个粒子推向 pbesti和 gbesti的统计加速度权重，两者均为正值。此外，粒子的速度 vi被一个最大速度Vmax所限制。

2.2 GLBest-PSO算法

研究表明［6-8］:若PSO算法过早收敛，粒子速度将下降至0，粒子群将趋于当前的极值，而它们往往为局部极值，尚未达到全局最优。因此对算法的改进不能着眼于收敛性，而应调节算法的搜索范围，以及全局和局部搜索能力。对全局搜索，通常好的方法是在前期具有较高的探索能力以得到合适的粒子，而在后期有较高的开发能力以加快收敛速度。鉴于惯性权值对粒子速度的影响以及c1和c2是决定粒子“认知”和“社会”能力的关键参数［5-6］，文献［9］中提出了一种改进的PSO算法，该算法中，惯性权重w，加速常数 c1和 c2既不取恒值，也不随进化次数的增加而线性变化，而是表示成局部最优和全局最优的适应度函数:

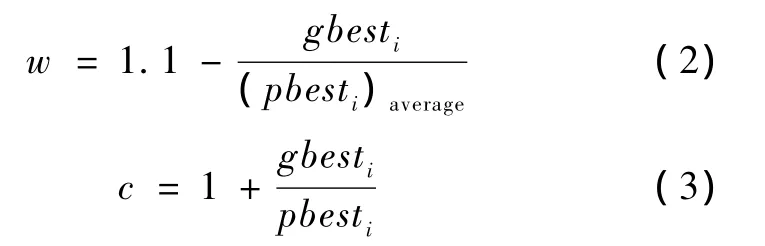
式中，w为每个进化代数的惯性权重;c为每个进化代数的加速度常数;(pbesti)average为该进化代数对应的所有粒子历史最优位置的平均值。式(2)为全局-局部平均最优惯性权重;式(3)为全局-局部最优加速度常数，则相应的速度更新表达式为:

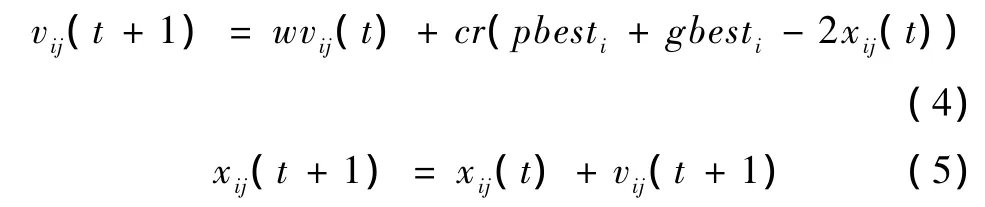
式中，r为［0，1］的随机数，式(2)～式(5)称为GLBest-PSO算法。

可以看出，当全局最优值等于局部最优值时，全局-局部平均最优惯性权重的值达到最小，这实际上使粒子在全局最优值附近搜索，并迅速地向最优值收敛。同样，当全局最优值等于局部最优值时，全局-局部最优加速度常数等于2，并且在整个搜索过程中，其值始终位于2附近。这两个参数帮助算法提高搜索精度和效率，获得更佳的寻优性能。

3 基于GLBest-PSO算法热工过程模型辨识

热工过程模型的传递函数为［4］:

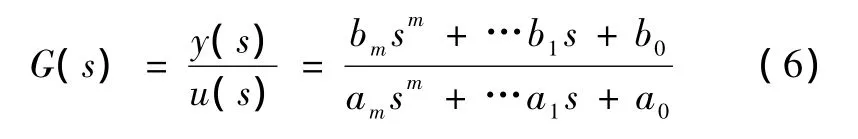
式中，y(s)和u(s)分别是过程的输出和输入函数;bm，…，b1，b0和 am，…，a1，a0分别是 y(s)和 u(s)表达式对应的系数。由于热工对象的时间常数大、阶次高，各参数 ai间的数量级相差较大，难以确定各参数的合适范围，因此直接利用式(6)进行参数辨识时，往往寻优时间长，辨识精度低，难以获得好的效果。为此，可以结合热工过程的特性，对于有自衡和无自衡的传递函数为［4］

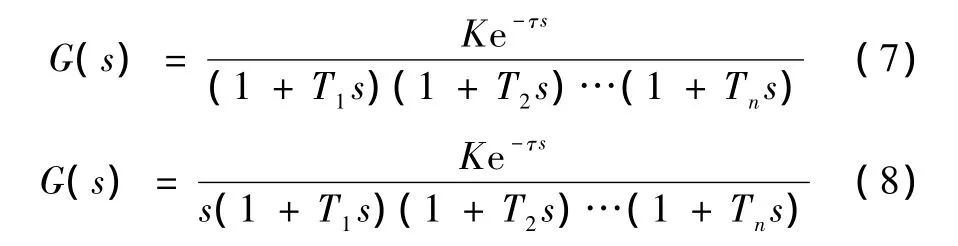
文中需对 T1，T2，…，Tn，K，τ进行寻优，根据热工过程特性和已有经验，可以确定模型的时间常数T1，T2，…，Tn∈［0.01，100］，过程纯滞后时间 τ∈［0，300］，对象静态增益 K∈［0.01，100］。为与文献［4］中的GA进行比较，本文取与其相同的目标函数:

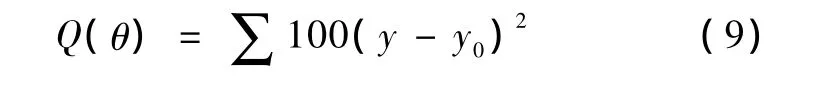
式中，y和y0分别是实际对象输出和模型输出。对热工过程的模型辨识就是寻找最优参数 θ=［T1，T2，…，Tn，K，τ］，使 Q 值最小化。

实例一:选取文献［4］中的热工过程实例:

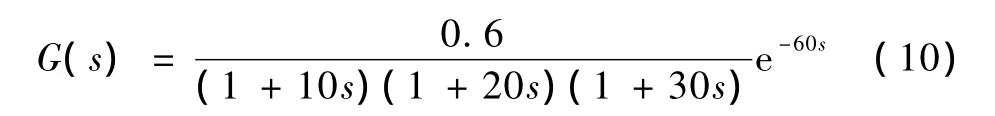
算法的参数设置为:群体规模m=20，群体初始速度和初始位置在取值范围内随机产生，i=1，2，…20，w和 c的初值在取值范围内随机产生，r在［0，1］之间随机产生，需对［T1，T2，T3，K，τ］五个参数寻优，所以搜索空间维数D=5，仿真时间长为300s，采样周期为1s，算法的终止条件与文献［4］相同，即最大搜索步数L=70或目标函数值 Q＜0.2。3次辨识结果见表1。表2是GA所对应的辨识结果［4］。

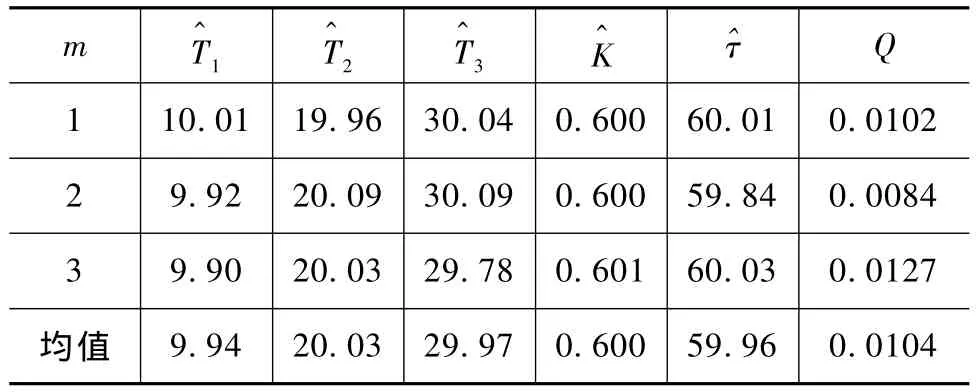
表1 GLBest-PSO在阶跃输入下的辨识结果(三阶)Tab.1 Identification results of step input with GLBest-PSO(Step 3)

由表1和表2可知，用本文算法得到的结果较GA更接近于真值，辨识误差小于GA的辨识结果。

为验证算法的稳定性，对该对象进行50次试验，图1是GLBest-PSO算法和GA每次辨识结果所对应的目标函数值。n是实验次数，Q是对应的目标值。可以看出，用GLBest-PSO算法进行辨识时，目标函数值及变化范围较小，算法更稳定。

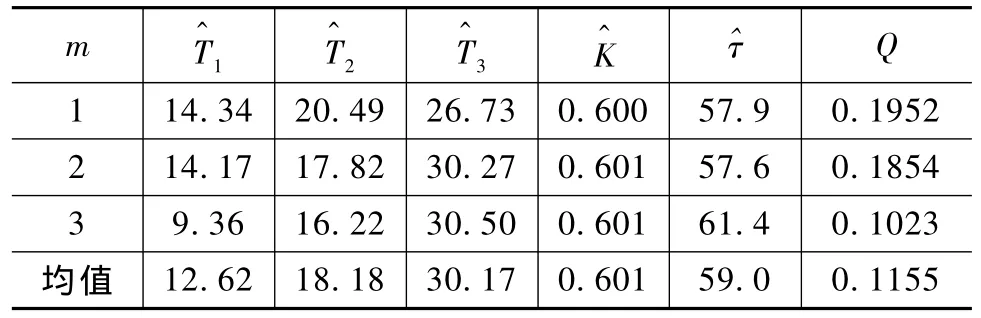
表2 GA在阶跃输入下的辨识结果(三阶)Tab.2 Identification results of step input with GA(Step 3)

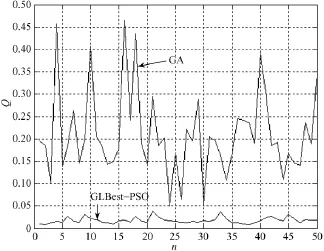
图1 50次实验下对应的目标函数值Fig.1 Objective function value for 50 times experiments

当模型阶次变化时，可得到表3所示的二阶、四阶、五阶辨识结果及准则函数值。表中n为设定的模型阶次，L为算法终止时的搜索步数。由表3可知，当辨识阶次大于实际阶次时，误差较小，模型辨识结果与过程真值较接近。当辨识阶次小于对象实际阶次时，辨识误差相对较大，但仍在允许范围内;可见，本文算法用于模型参数辨识时，在模型阶次不匹配时，辨识误差虽增大，但仍在允许范围内，因此可以认为其对模型阶次的敏感性不强。

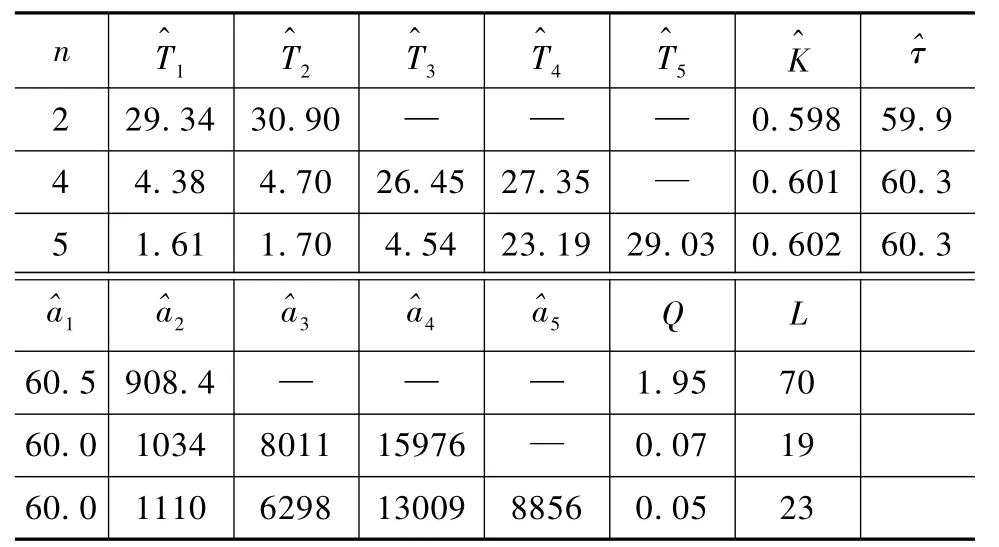
表3 GLBest-PSO在阶跃输入下不同阶次辨识结果Tab.3 Identification results of step input with GLBest-PSO for different step

用随机阶跃信号、含噪声的阶跃信号、正弦信号等作为辨识信号，结果见表4，可以看出，对于其他输入信号，本文方法都能得到满意的效果。

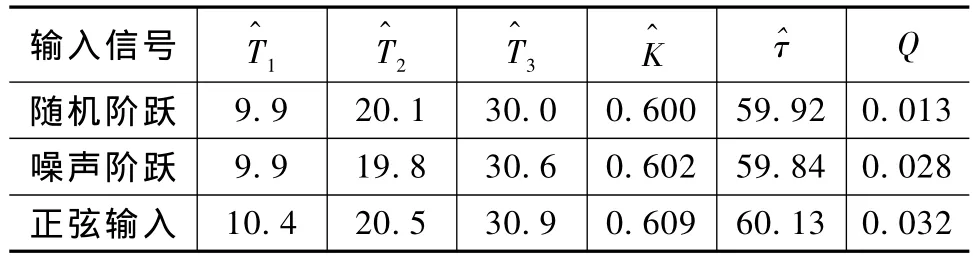
表4 GLBest-PSO在多种输入信号时的辨识结果Tab.4 Identification results of different input signals with GLBest-PSO

对该例的仿真结果表明，对于大时滞的对象或过程，用本文提出的方法进行模型参数辨识时，可以得到满意的结果。

实例二:球磨机是燃煤电厂制粉系统中的常用设备，它是一个具有非线性、大滞后、强耦合和具有多种不确定性扰动的多变量对象，对其建模难度大，造成自动控制系统的投用率低。本节以该系统的主要环节——机内存煤量过程为例，采用GLBest-PSO算法进行过程建模。

对于磨煤机内存煤量控制回路，经现场实验测试和分析，得到如表5所示的300s内的单位阶跃输出观测数据。

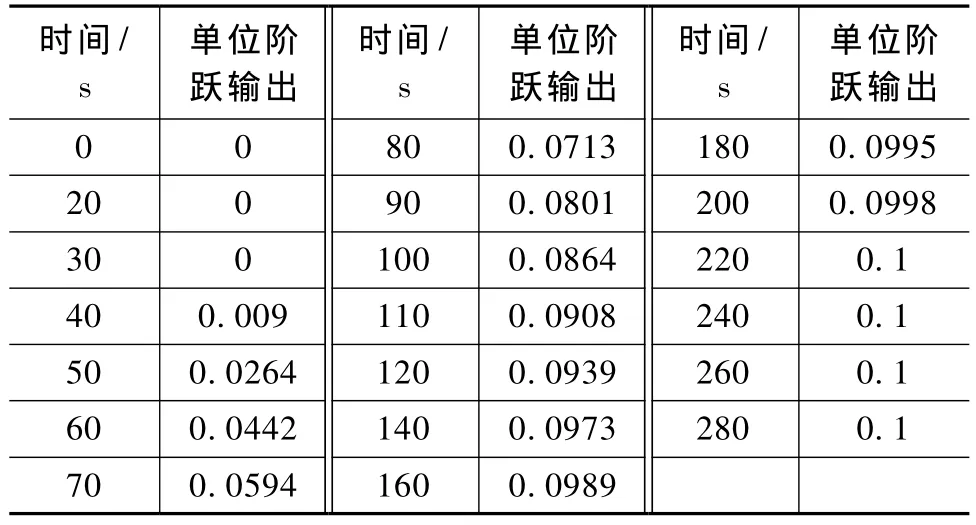
表5 单位阶跃输入下过程输出Tab.5 Process output of step input

以表5的观测数据来进行GLBest-PSO算法建模仿真实验，GLBest-PSO算法参数设置和终止条件与前述相同。表6是不同阶次的辨识结果，表7是利用文献［4］中的 GA方法所得到的结果。其中 n是辨识阶次，L是算法终止时算法已循环次数。图2是实际过程单位阶跃响应输出和二阶模型单位阶跃响应输出结果。

从图表中可以看出，无论从准则函数值还是算法终止时的循环次数，GLBest-PSO算法均优于GA。用GLBest-PSO算法对该回路对象进行建模时，可得到较为精确的模型，辨识效果较好。

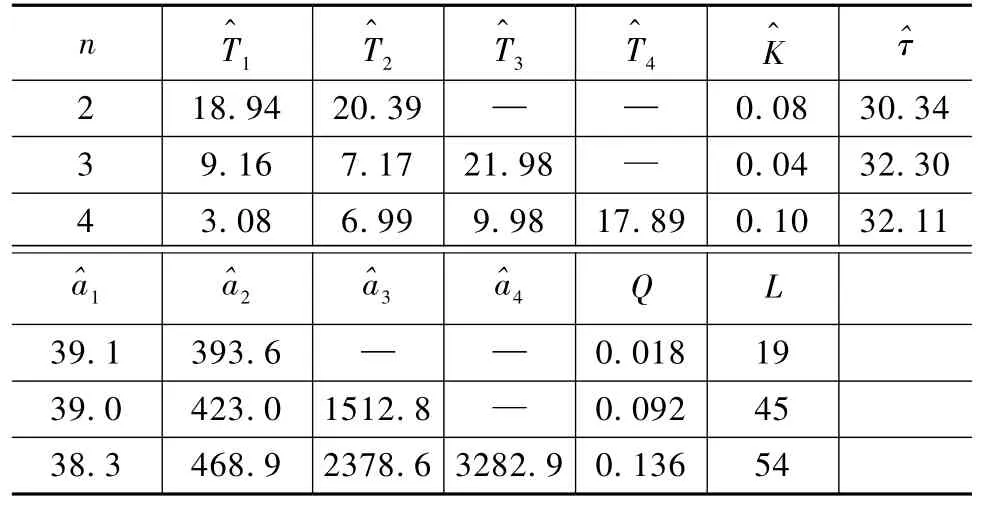
表6 GLBest-PSO在阶跃输入下不同阶次辨识结果Tab.6 Identification results with step input with GLBest-PSO

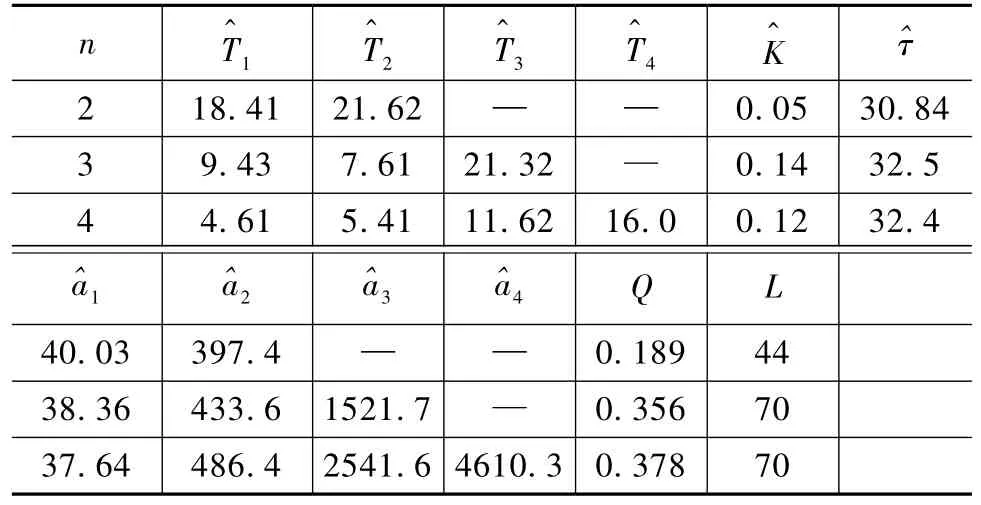
表7 GA在阶跃输入下不同阶次辨识结果Tab.7 Identification results with step input with GA

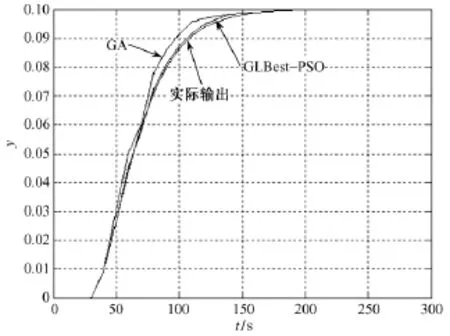
图2 单位阶跃输入下实际过程与二阶模型输出Fig.2 Actual process and step 2 model output of step input

4 结论

被控对象数学模型的精确辨识对火电厂控制系统的设计和优化具有重要意义。本文研究了GLBest-PSO算法在热工过程模型辨识中的应用，结果表明该算法可有效地辨识模型参数，方法简单，收敛速度快，计算量小，辨识精度高，该方法对解决热工过程系统的建模问题具有潜在的实用价值。

［1］Golub G H，Van Loan C F.An analysis of the total leastsquares problem［J］.SIAM J.Numer.Anal.，1980，17(6):883-893.

［2］Felsenstein J.Evolutionary trees from dna sequences:A maximum likelihood approach［J］.J.Mol.Evol.，1981，17(1):368-376.

［3］王田，薛建中，习志勇，等(Wang Tian，Xue Jianzhong，Xi Zhiyong，et al.).基于RBF神经网络辨识的过热蒸汽温度控制(Control of superheated steam temperature based on RBF neural network identification)［J］.热力发电(Thermal Power Generation)，2008，37(10):87-91.

［4］刘长良，于希宁，姚万业，等(Liu Changliang，Yu Xining，Yao Wanye，et al.).基于遗传算法的火电厂热工过程模型辨识(Model identification of power plant thermal process based on genetic algorithm)［J］.中国电机工程学报(Proceedings of the CSEE)，2003，23(3):170-174.

［5］Kennedy J，Eberhart R.Particle swarm optimization［A］.Proc.IEEE Int.Conf.on Neural Networks［C］.Perth:IEEE Press，1995.1942-1948.

［6］Shi Yuhui，Eberhart R.A modified particle swarm optimizer［A］.Proc.IEEE Int.Conf.on Evolutionary Computation［C］.Anchorage:IEEE Press，1997.303-308.

［7］Clerc M，Kennedy J.The particle swarm explosion，stability，and convergence in a multidimensional complex space［J］.IEEE Transactions on Evolutionary Computation，2002，6(1):58-73.

［8］Ratnaweera A，Halgamuge S K，Watson C.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficient［A］.IEEE Trans.Evolutionary Computation［C］.IEEE Press，2004.240-255.

［9］Senthil Arumugam M，Rao M V C.A new and improved version of particle swarm optimization algorithm with global-local best parameters［J］.Knowledge and Information Systems，2008，16:331-357.