基于可分解的卷积核和快速傅立叶变换FFT的指纹图像增强算法*

黄东运 钟震宇 曹永军 黎伟权

（广东省自动化研究所）

基于可分解的卷积核和快速傅立叶变换FFT的指纹图像增强算法*

黄东运 钟震宇 曹永军 黎伟权

（广东省自动化研究所）

指纹识别系统在图像增强阶段涉及很多卷积运算，占用大量的计算时间。在不利用专门的DSP处理器进行指纹图像增强处理情况下，常规的卷积运算计算时间非常长。在指纹图像增强过程中，卷积运算主要集中在方向场估计和高波滤波两个阶段。为此本文提出了一种指纹图像增强算法，利用可分解的卷积核和快速傅立叶变换来替换常规的卷积运算，可减少算法的时间复杂度，快速实现指纹图像增强。

高斯梯度算子；高波算子；高波滤波；卷积核分解；快速傅立叶变换

1 引言

指纹识别技术是生物识别领域应用最广的识别技术，大部分指纹识别系统采用指纹特征点匹配的方式进行个人身份识别。特征点为指纹脊线中的末端点或分叉点。可靠的特征点提取在指纹分类和识别中起着非常关键的作用。

指纹图像增强的主要目的是使脊线尽可能清晰和自然，保持指纹特征点的原始特征。指纹增强过程中，不能产生人为的伪特征或噪声，不能引起特征点的丢失。目前认为最可靠并被普遍接受的图像增强方法一般采用与局部图像特征相关的滤波方法进行，其中最广泛使用的是高波滤波。使用高波滤波可以连接断裂的脊线，恢复由于灰尘或污损引起的质量较差区域的脊线图像。

高波滤波与局部指纹图像的空间频率及方向紧密相关。在进行滤波操作之前，需要对指纹区域进行脊线方向和频率估计，然后根据指纹局部区域的方向和频率信息选择相应的高波滤波器进行卷积运算，达到图像增强效果。在局部指纹图像方向估计过程中，主要利用x和y两个方向的梯度滤波器分别进行滤波，再根据两个方向的梯度信息，对局部区域进行方向估计。频率估计在脊线方向估计完成后进行，将局部区域的指纹图像在垂直于脊线方向进行投影，计算一维波形图中峰值之间的平均距离，即可获得其频率信息。因此，在图像增强过程中涉及大量卷积运算，计算量非常大，需要的计算时间非常长，必须选择合适的算法来代替常规的卷积运算，减少计算时间，满足指纹识别系统中实时性要求。

为了降低卷积运算的计算量，本文提出的算法利用可分解的滤波器和傅立叶变换的卷积特性，在方向场估计和高波滤波两个阶段进行算法优化，降低时间复杂度，实现快速指纹图像增强。

2 指纹图像增强过程

基于特征点的指纹识别过程一般包括指纹区域检测、脊线方向、频率估计、图像增强、指纹图像二值化和脊线细化、特征点提取和编码、模式匹配等。在这些处理过程中，大部分计算量集中在指纹特征点提取之前即图像增强阶段。图1显示了指纹图像增强过程中每个阶段图像的处理结果。

图1 指纹图像处理前、后的图像

图1中，(b)和(c)在空间结构上与原始图像(a)稍微发生形变，这是由于在算法中，采用统一的脊线频率值即经验值。当脊线频率值与实际的局部指纹图像脊线频率有差异时，在高波滤波以后会产生形变。但算法很好地保证了指纹特征点（末端点和分叉点）的完整性，并连接了脊线断开点。

3 方向场估计

指纹方向场是指纹图像增强过程中的重要部分，指纹图像方向场估计的结果是一个二维浮点数据类型矩阵，维度与原始图像数据矩阵一致，每个像素对应的方向值，是动态选择高波滤波器的依据。本文采用Lin Hong等[1]提出的最小均方方法来估计指纹脊线的局部方向。给定一个指纹图像G，方向场估计的主要步骤如下：

② 以像素（i，j）为中心，区域大小为w×w，计算每个块的局部脊线方向θ(i,j)：

为了算法优化，选用可分解的高斯梯度算子，将二维算子分解成两个一维的算子，利用快速傅立叶变换以及逆变，实现第一阶段需要的卷积运算。

3.1 高斯梯度算子

高斯滤波器在数字信号处理中被广泛应用。在数字图像处理中，通过该滤波器进行滤波可起到消除噪声、平滑图像的效果。其二维的高斯滤波器定义如下：

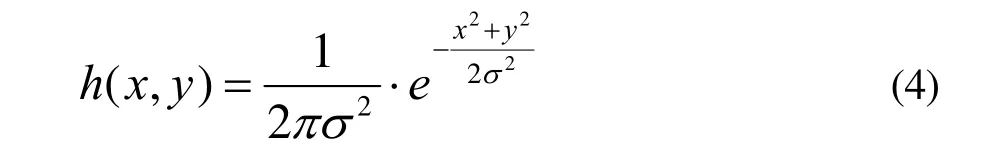
其中，x为原点到水平轴的距离；y为原点到垂直轴的距离；σ为标准的高斯分布标准方差。分别对式（4）进行x和y方向求导，可获得两个方向的梯度算子公式。

考虑其对称性，下面只给出一个方向的梯度算子分解过程。对式（4）进行x方向的求导，可以得该方向的梯度算子：

3.2 傅立叶变换

傅立叶变换是一种线性的积分变换，能将满足一定条件的某个函数表示成三角函数（正弦或余弦函数）及其积分的线性组合。傅立叶变换具有多种不同变体形式如连续傅立叶变换、离散傅立叶变换。连续傅立叶变换将平方可积的函数f(t)表示成复指数函数的积分或级数形式：

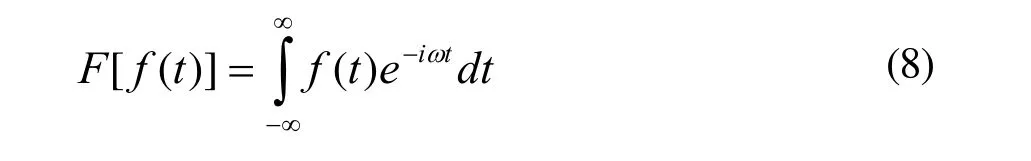
式（8）将频率域的函数F（ω）表示为时间域的函数f（t）的积分形式。在数字图像处理领域，一般采用离散傅立叶变换，变换函数表示为求和形式：

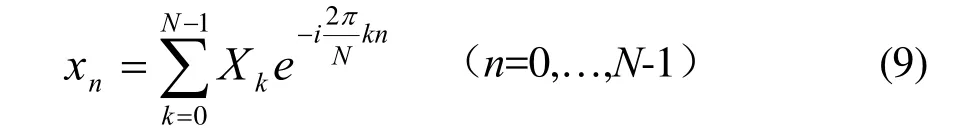
其中，Xk是傅立叶振幅。

傅立叶变换可以将复杂的卷积运算转换为简单的乘积运算，从而提供了一种简单的方法计算卷积。卷积定理指出：函数卷积的傅立叶变换是函数傅立叶变换的乘积。即一个域中的卷积相当于另一个域中的乘积，例如时域中的卷积就对应于频域中的乘积。

对于长度为n的序列，在进行离散傅立叶变换的时候，其计算复杂度为O(n2)，而利用快速傅立叶变换将序列变换到频域上以后，只需要一组对位乘法，总的计算复杂度为O(nlog(n) )。

4 图像增强

在获取了指纹图像的方向场和指纹频率后，需要将指纹图像与高波滤波器进行卷积运算，对图像进行滤波，以达到图像增强目的。

4.1 高波滤波

高波函数形成的二维高波滤波器具有在空间域和频率域同时取得最优局部化的特性，能够很好地描述对应的空间频率及方向选择性的局部结构信息，在数字图像处理领域，常用于纹理图像的分割和增强。

指纹图像由很多平行的脊线组成，很好地定义了纹理的频率和方向，并且在局部区域，由脊线和间隔区组成的正弦波形在方向变化上呈连续性。因此，带通滤波器仔细调整对应的频率和方向，完全可以保持指纹脊线结构，并且可以移除不需要的噪声。高波滤波器具有的频率选择性和方向选择性非常适合作为带通滤波核增强指纹图像。

常用的偶对称二维高波滤波器可表示为：

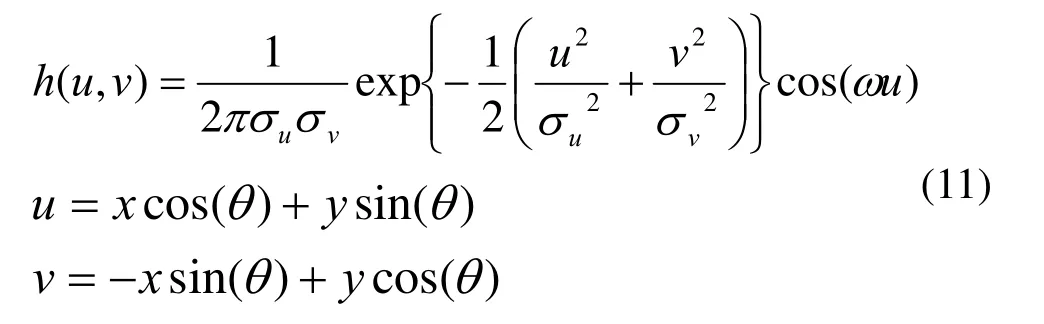
其中，θ为高波滤波器的方向；uσ和vσ分别为高斯包络在u轴和v轴上的标准差（u轴平行于θ、v垂直于θ）；ω为调制频率。图2是偶对称的高波滤波核形状。

对于长度为m、宽度为n的高波滤波器来讲，用常规的卷积方法实现高波滤波的计算复杂度为其计算量非常大，需要进一步对高波滤波算法进行优化。

4.2 高波滤波核分解

陈小光等[2]描述了高波滤波器的正交分解和非正交分解。本文采用了其正交分解的方法。根据式（11）将二维的高波滤波器进行正交分解：

使用按照公式（13）和（14）生成不同方向的滤波核，对指纹图像分别进行两次一维滤波，其时间复杂度为

5 实验结果

在系统中，对指纹频率估计阶段进行简化。根据指纹传感器的分辨率，采用经验值，对频率进行估计。在指纹脊线方向估计阶段，采用可分的卷积核，将二维卷积核分解为一维卷积核，然后使用快速傅立叶变换以及逆运算实现普通的卷积运算，降低时间复杂度。

在高波滤波阶段，将二维高波滤波器进行正态分解为两个一维滤波器。卷积运算中，根据像素对应的脊线方向动态选择对应的滤波核进行滤波。大于180°的卷积运算与反方向小于180°的方向运算结果相同，在实际卷积核制作中，只需考虑0°～180°的卷积模板的计算，从而减少系统的空间复杂度。每隔3度生成一对卷积核，总共生成60对卷积核。

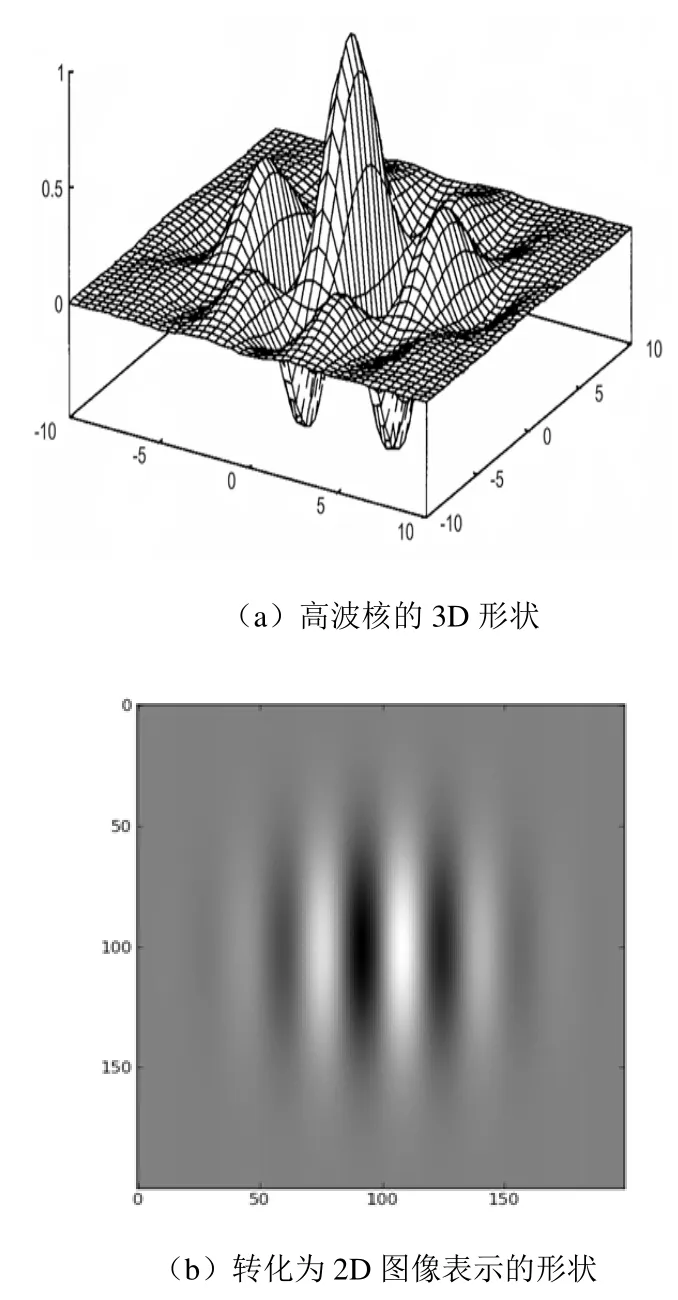
图2 偶对称的高波滤波核形状

实验主要分成3组进行，分别使用二维卷积运算；分解后卷积运算；快速傅立叶变换三种不同的卷积方法。实验在WINDOWS XP操作系统的PC机上进行，该机基本配置为2.0G主频，512M物理内存。实验结果如表1所示。

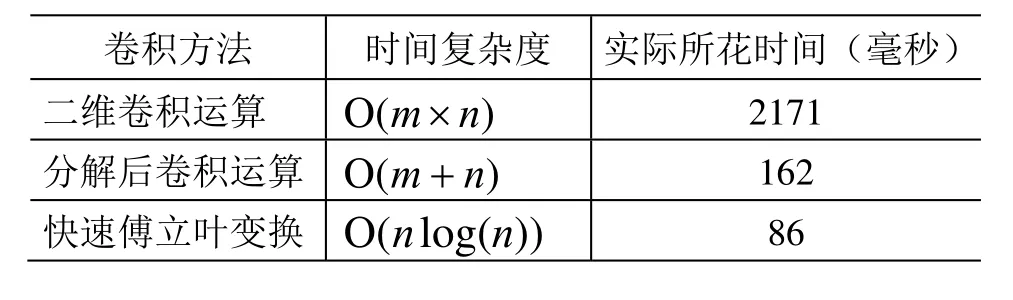
表1 不同方法进行指纹图像增强的实际测试结果

6 结论

使用具有各向异性的高波滤波器进行指纹图像滤波，达到指纹图像增强是指纹识别系统中广泛采用的图像增强方法。该图像增强方法涉及大量的卷积运算，本文利用可分解的滤波器和快速傅立叶变换代替常规的卷积运算，实现指纹图像的快速增强。本文提出的算法在下面几个方面进行了优化：

(1) 使用可分解的高斯梯度算子和快速傅立叶变换代替常规的卷积运算，有效地对指纹图像的方向场进行估计，降低了时间复杂度；

(2) 高波滤波器带有明显的方向选择性，虽然在分解后无法直接使用快速傅立叶变换实现常规卷积运算，但根据像素所在的脊线方向，动态选择分解后的一维高波滤波器进行两次滤波，同样极大地减少了计算时间。

实验结果表明，在经过指纹方向场估计和高波滤波两个阶段优化以后，本文提出的算法是非常有效的，达到了快速指纹图像增强目的。

[1] Lin Hong, Yifei Wan, Anil Jain. Finger Image Enhancement: Algorithm And Performance Evaluation. Pattern Recognition and Image Processing Laboratory. Department of Computer Science, Michigan State University,1998: 10-11.

[2] 陈小光,封举富.Gabor滤波器的快速实现[J].自动化学报,2007,33(5):457-458.

Fingerprint Image Enhancement Based on Decomposable Kernels and Fast Fourier Transforms

Huang Dongyun Zhong Zhenyu Cao Yongjun Li Weiquan
(Institute of Automation, Guangdong)

In a fingerprint verification system, enhancing fingerprint images needs lots of convolutions which take plenty of computation. Without help of any specialized digital signal processor to tackle this task, it takes a very long time for generic convolutions. There are two stages in the fingerprint image enhancement involved with heavy convolution. In this article, instead of classic methods, we use decomposable kernels and fast Fourier transforms to realize convolutions in the stages of estimating orientation field and Gabor filtering for fingerprint image enhancement, which enable us to reduce the time complexity and achieve a faster computation.

Gaussian Gradient Operator; Gabor Operator; Gabor Filtering; Convolutional Kernel Decomposition; Fast Fourier Transforms

黄东运，男，1975年生，硕士，研究方向：机器视觉、图像识别。

钟震宇，男，1971年生，博士，研究方向：运动控制、嵌入式系统。

曹永军，男，1981年生，硕士，研究方向：运动控制、图像识别。

黎伟权，男，1982年生，硕士，研究方向：运动控制、图像识别。

广东省科技计划项目（2010A040306005，2011B010300021）；广东省中国科学院全面战略合作项目（2011B090300054）；广东省科学院青年基金项目（qnjj20097、qnjj201014）。