有关光电头盔瞄准具的误差校正方法

臧 赜，陶忠祥

(空军航空大学 军械系，长春 130000)

头盔瞄准具是装在飞行员头盔上的一种瞄准装置，它使用方便、瞄准迅速、能充分发挥人的作用，根据具体装备的功能、结构、技术的不同有不同的名称，但其目的是一样的。随着飞行员的头部转动，测量装置可以实时测量瞄准线相对于飞机正方向的角度，然后根据该角度控制导弹的导引头对准目标进行发射。我军战机装备的光电头盔瞄准具有多个型号，既有国产的也有进口的，但这些瞄准具的目标角坐标测量原理均相同，所不同的仅是机械结构和电子处理系统。由于此种光电头盔瞄准具的工作原理比较复杂，使得其测量精度受到多种因素的影响，精度的调整过程复杂，难以在部队真正有效实施，战时情况下会严重影响设备的正常使用。本文针对其基线误差、测角原理误差，这些由十棱镜转轴的非共面偏转引起的误差现象作了具体分析，并提出了校正的理论公式和方案。

1 基线校正

基线是指2 个扫描装置同时扫描到某一个发光二极管时，2 条扫描光线在十棱镜反射面上的反射点之间的连线(如图1 所示)。实际的基线值就是这2 点之间的距离，它随十棱镜的转动而不断变化，是进行误差校正时必须校正的一个重要参数。

图1 基线形成过程示意图

在工程实践中要考虑工程误差。理论上的扫描部件是一个无限细的轴，而实际上扫描棱镜是一个电机带动的实体多面棱镜。当扫描接收线扫过不同的角度时，各扫描线并不一直相交于一点。

因此，在计算K 值时，无法确定固定值基线长度。所以基线长度是动态变化的，但无论如何变化，都要保证辐射管投影点坐标的计算要在统一的坐标系下，所以，当基线位置改变时，还要对坐标修正(如图2 所示)。

图2 基线校正原理框图

基线的位置规定为:

任意时刻

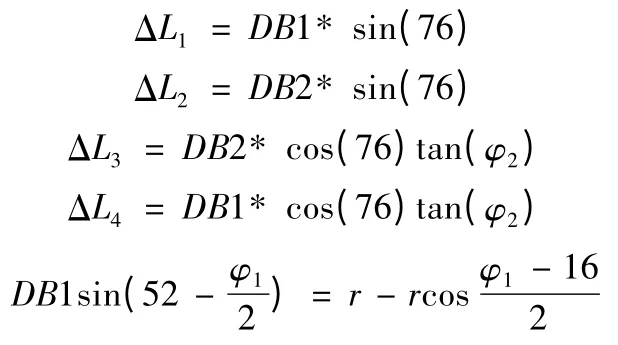
修正后的基线长度

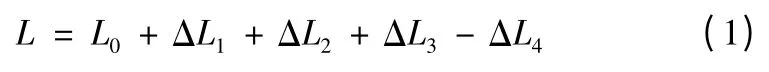
通过上面的分析可以看出，在不考虑其他因素影响的条件下，头盔瞄准具测角误差主要来自对于基线长的计算误差。而此误差是由计算原理公式的不正确引起的，属于系统误差。该误差通过函数传递，最终在方位角和俯仰角的结果中产生了函数误差。设基线长为L，则方位角γ 可表示为γ=f(L)。则根据高等数学可知，其增量可用函数的全微分表示，即假设测量基线时的系统误差为ΔL，由于该误差值较小，可用来近似代替微分量dL，从而得到函数的系统误差Δγ 近似为

因此有，

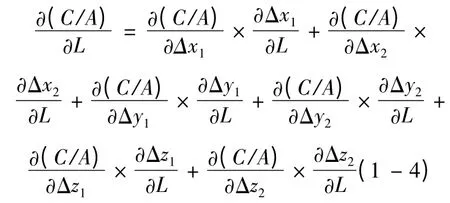
从而

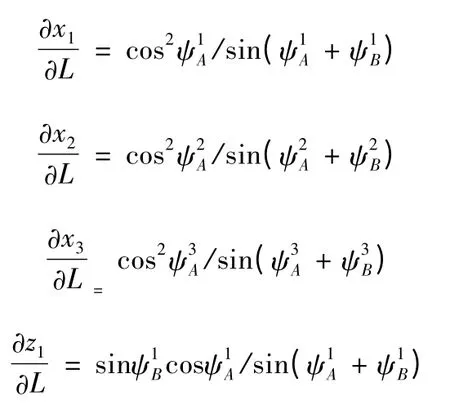
测量基线长所产生的系统偏差

其中Δγ 的值可以通过经纬仪测量出的标准方向角的值和头瞄计算出的方向角的差值确定。这样通过一系列的推导，便计算出了工程实现过程中系统误差的大小。根据计算出的误差值反带回方位角和俯仰角的理论计算公式便可计算出由基线长所产生的方位角和俯仰角计算误差大小。

2 测角校正

测角原理是指确定头盔观测装置上的3 个红外发光二极管，相对于扫描装置轴YCA、YCB所转过辐射源方位角的原理。

扫描装置的电动机通过减速齿轮带动十棱镜、活动分度盘转动。当活动分度盘和固定分度盘标线不断地对准时，发光二极管发出的光线被光敏二极管接收，电路中即产生出2组1°读数脉冲和1 组36°基准脉冲。这些脉冲信号经过随动装置电路处理，最后得到呈矩形波的1°A、36°A、1°B、36°B读数、基准脉冲序列。

当十棱镜转动时，其反射面依次扫过扫描区。也就是其瞬时视场依次扫过形成水平60°、垂直35°的扫描视场。十棱镜每转过1 周，将完成10 次扫描。当瞬时视场扫描到头盔观测装置上的某个红外发光二极管时，该管辐射的红外脉冲就会进入扫描装置的光学系统，而被光敏接收器接收到;电路中即产生出脉冲信号，再经主通道放大器处理最后得到测量脉冲序列SA、SB。测量脉冲序列SA、SB中，包含有3 个红外发光二极管辐射红外脉冲的响应信号。脉冲序列1°A、36°A、1°B、36°B、SA、SB，输给电子装置，经电子装置电路处理，从SA、SB中区分开分别属于3 个红外发光二极管的扫描脉冲序列SKA1～SKA3、SKB1～SKB3和有用信号SA1～SA3、SB1～SB3，并判明有用信号中心相对应的十棱镜反射面所转过角度αAi、αBi。

由于十棱镜反射面的非共面定轴转动，使得十棱镜中心实际位置与理论位置及虚拟位置产生了一定的偏差，如图3所示。

图3 测角原理误差的产生示意图

图3 表明该型头盔瞄准具为扫描3 个发光二极管辐射的红外信号，采用2 个垂直轴相距OAOB= L0、内切圆半径r=19 mm 的十面棱镜的机电扫描仪，称L0为头位测量基线。

值得注意的是，由于十棱镜反射面偏离转轴19 mm，扫描测量时，非共面定轴转动的反射面，在旋转的同时会产生纵向和横向位移，因此测量出的扫描角度并不是相对扫描装置的轴线转过的角度ΨAi、ΨBi，而是相对十棱镜反射面中心转过的角度φAi、φBi，这样就会产生测量误差，它对实际信号的产生和最后输出角度的精度都有直接影响，因此需要根据扫描角度值进行校正，以确保目标方位角和目标俯仰角计算精度。

测角校正的基本原理是在确定理论基线L0的前提下，根据扫描部件测定的φAi的值，确定出头位测量数学模型所需要的ΨAi、ΨBi值。

如图4 所示，OA、OB为左、右扫描部件十棱镜回转中心。发光二极管i 绕十棱镜垂直轴转过的角度为ΨAi、ΨBi，扫描部件测定的二极管辐射光线转过的角度为φAi、φBi。发光二极管i 的辐射光线与OAXA、OBXB轴相交于eAi、eBi处。

图4 测角校正原理框图

利用式(3)～(8)，可求出头盔位置的数学模型所需要的ΨAi、ΨBi。

3 结论与分析

根据系统误差的相关理论计算出了基线长系统误差ΔL，根据误差传递原理，基线长误差ΔL 经函数传递最终产生了实际应用中的方位角和俯仰角误差。若ΔL 装订回头盔瞄准具系统中进行重新计算，便可以得到补偿后的方位角和俯仰角，从而完成了系统误差的自动调整，整个自动调整过程如图5 所示。

图5 头瞄系统误差自动调整过程

对于光电式头盔瞄准具测量原理产生的基线误差和测量角误差的分析与提出的校正方案，都可以对部队有关光电头盔瞄准具的研究和技术改造贡献参考和建议。

［1］巩平，张光才，李颖. 军用头盔面面观［J］. 环球军事，2007(2):53-55.

［2］魏庆，张峰国.军用头盔的发展［J］.军事大观，2005(5):77-78.

［3］李雪丽.计算机实时监测的电磁定位系统的研究［D］.北京:北京交通大学，2008.

［4］Mohamed Zaoui，Dean Wormell，Yury Altshuler，et al. A 6 D.O. F. Opto-Inertial Tracker For Virtual Reality Experiments In Microgravity［J］.Anta Astronautic，2004，49:451-462.

［5］Eric Foxlin. Head-tracking relative to a moving vehicle or simulator platform using differential inertial sensors［J］.Proceedings of SPIE，2004，5324:133-144.

［6］Eric Foxlin，Michael Harrington，Yury Altshuler. Miniature 6DOF inertial system for tracking HMDs［J］.Proceedings of SPIE，2005，5478:214-228.

［7］Park W S，Cho H S，Byun Y K，et al.Measurement of 3-D position and orientation of rigid bodies using a 3-facet mirror［J］.Proc.of SPIE，2007，6934:14-19.

［8］陶忠祥. 位置敏感探测器在头位跟踪中的应用研究［D］.长春:中国科学院，2004.

［9］Constantine T. Markos，John J. Atkinson，Gerry Wyntjes.All-optical helmet tracker for multi-craft multi-vehicle systems［J］.Proceedings of SPIE，2003，5079:86-94.

［10］Don S.Odell，Vlad Kogan.Next Generation High Accuracy Optical Tracker For Target Acquisition and Cueing［J］.Proceedings of SPIE，2006，62:1-10.

［11］田晓焱.基于机器视觉的头盔瞄准具转动角度的侧量［D］.西安:西北大学，2006.

［12］孟举. 基于视频图像处理的头部位置跟踪算法研究［D］.西安:西北工业大学，2007.

［13］王超，魏生民，周继红，等.视频图像技术在头部位置跟踪上的应用研究［J］. 现代制造工程，2008(2):111-115.

［14］Douglas L.Franck.Eye tracking equipment development for helmet mounted displays on tactical aircraft［J］. Proceedings of SPIE，1998，3362:235-242.

［15］Claudia Mello-Thomas. Remote vs. Head-Mounted Eye-Tracking:A Comparison Using Radiologists Reading Mammograms［J］.Proceedings of SPIE，2007，61:1-8.

［16］Aleksandr Sergeyev.Design of the Stereoscopic Eye-Tracking System for Quantities Remote Sensing Applications［J］.Proceedings of SPIE，2008，708:1-9.