基于数学模型的压气机叶片积垢研究

王冠超，李冬，刘晓东

基于数学模型的压气机叶片积垢研究

王冠超1，李冬2，刘晓东3

(1.海军驻长春地区航空军事代表室，吉林长春300000；2.海军航空工程学院研究生管理大队，山东烟台264001；3.海军航空兵学院，辽宁葫芦岛125001)

对压气机叶片积垢数学模型进行比较分析，选取平板叶栅-恒定速度模型为积垢计算模型。提出了压气机各级积垢分布的数学模型，并对压气机的积垢敏感性进行分析。以0～20µm尺寸的积垢微粒为研究对象，针对叶片不同积垢微粒尺寸分布模型，通过仿真得到了压气机各级积垢无因次化质量分布模式，和不同叶片条件下的层积垢累积率。仿真结果表明：积垢与压气机各级的几何尺寸和流动特性密切相关，积垢微粒尺寸分布是决定积垢水平的重要因素。本研究可为压气机叶片积垢研究提供参考。

压气机；积垢；模型；层积垢累积率；敏感性

1 引言

压气机性能衰退直接与其叶片形状改变密切相关，而叶片形状的改变往往是由积垢、腐蚀、侵蚀和外物损伤等引起[1，2]，其中叶片积垢占很大比重。压气机叶片积垢后，附着在压气机叶片上的微粒会增加叶片表面的粗糙度，使压气机气路中产生湍流。并且随着积垢的增多，其直接后果就是压气机压比减小和叶片有效攻角增加，严重时甚至引发喘振。轴流压气机中，积垢将导致叶片前缘形状和表面粗糙度改变，进而使压气机各级气流流动偏离设计状态，改变压气机特性。文献[3]、[4]对压气机叶片由于积垢造成的性能衰退进行了研究，本文在此基础上对三种叶片积垢模型进行比较分析，选择一种较合适的模型作为后续计算模型。对于压气机叶片积垢微粒尺寸分布的不同模式，以0～20 μm尺寸的积垢微粒分布模型为研究模型，得到了不同条件下层积垢累积率的变化情况。提出了压气机各级积垢相对量的数学模型，并以此得到压气机各级的无因次化累积质量。对压气机积垢敏感性进行了分析，从中发现其与轮毂比、压比的变化规律。

2 压气机叶片积垢的特征分析

2.1 积垢沉淀

积垢沉淀是指吸入发动机的空气中所含各种粉尘、微粒在液态物质的粘附效应作用下，在航空发动机叶片、通道壁等部件表面形成粘附和堆积[2]。其发生需要两个条件，一是吸入的空气中含有尘粒和粉尘；二是气路通道内含有液态物质。其中，危害性较大的尘粒主要是煤尘、水泥尘和飞尘三种[5]。研究中一般将空气所含各种尘粒和微粒按粒径d分为三类，即d≤2 μm、2 μm≤d≤20 μm和d≥20 μm。目前积垢微粒直径的分布模式如图1[6]所示，图中P为空气中微粒的体积质量。本文仅对图1(a)中三种微粒尺寸(0 μm≤d≤20 μm)分布模式进行研究。

2.2 层积垢累积率

假定叶片为圆柱形。微粒在流场中缓慢运动时，通常混合是主导现象；若微粒尺寸不明显小于圆柱尺寸，则脱离圆柱是主导现象。在高速流场中，若圆柱尺寸比微粒大得多，则微粒由于粘性力贴近圆柱是主导现象。研究中假设微粒粘附在圆柱上即为积垢。为检验贴近圆柱面微粒的污染效果，定义了层积垢累积率Ec(即粘附在圆柱面的微粒数目与所有进入圆柱面的微粒数目之比)，如图2所示。其中，H为粘附微粒的等价范围，L为进入流场的微粒范围。当微粒垂直靠近圆柱时，微粒由于惯性在圆柱面附近与流场分离或粘附在圆柱面上。同时假定流场中运动微粒均匀分布，且相撞后不弹开。

2.3 压气机各级积垢分布

图2 沿圆柱面微粒的运动特性Fig.2 Characteristics of particle motion around a cylinder

采用无因次化积垢质量aj作为评定各级中积垢含量的指标。aj指压气机各级中微粒(最小尺寸(0.1 μm)到最大尺寸(20 μm))累积的质量与第一级叶片积垢质量的比值。第j级中，aj表示为[6]：

式中：下标i为每级中第i个微粒，Pi为空气中第i种尺寸微粒的体积质量，Ni,j为粘附在第j级叶片上第i种尺寸微粒的数量。

3 压气机叶片积垢模型

3.1 圆柱叶片模型

此模型是把叶片看成圆柱形。考虑到气流在叶栅中而非单个叶片旁流动，微粒在圆柱叶片中的流动情形如图3所示。图中：ω为微粒进口相对速度，c为弦长，s为叶片间距，β1、βb分别为微粒进口角度和叶片级角度。

3.2 平板叶片模型[4]

假定叶片为平板，此模型能较好地反映出微粒在流场中的运动情况，如图4所示。

3.2.1 恒定速度模型

图3 轴流压气机中两叶片间的流动特性Fig.3 Flow characteristics between two blades in axial flow compressor

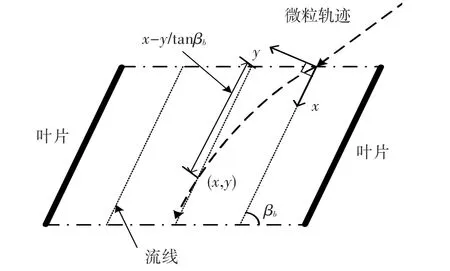
图4 假定压气机叶片为平板的简化模型Fig.4 A simplified model with assumption of blade as a flat-plate

进一步假定叶片间的流动速度恒定。x方向平行于叶栅，y方向垂直于叶栅。此时模型表示为[6]：

3.2.2 变速度模型

为说明叶片内部相对流动速度减小程度，此模型假定进出口流动速度满足w2/w1≥0.72，且沿着叶片流动速度线性下降。微粒在x方向运动的方程为：

综上，三种模型的某一尺寸微粒在叶片表面的积垢累积程度Ec1可用下式计算[4]：

式中：μ为动力粘性系数，ρ为微粒密度。

4 压气机积垢敏感性分析模型

为研究并度量压气机性能对积垢效应的敏感性，Tarabrin等定义了积垢敏感性指数ISF[7]：

由于ISF定义的推导比较复杂，故在推导过程中采用了一些经验性假设。式(5)中分子为压气机单级加功量，为便于使用和分析，采用压气机增压比来代替，并且暂不考虑平均温度变化ΔTAVG的影响。则上式可改为：

以上两式中：rhubrtip为轮毂比，Dtip为叶顶间隙，π为压比，nstage为压气机级数。

5 积垢模型和叶片积垢的仿真分析

以上三种叶片积垢模型的层积垢累积率如图5所示。由图中可知，三种叶片积垢模型得出的层积垢累积率都随积垢微粒尺寸的增大而增大。圆柱叶片模型的层积垢累积率比平板模型的略大，主要是因为圆柱叶片比平板叶片有更大的接触表面。变速度模型的层积垢累积率比恒定速度模型的大，微粒尺寸较大时更为明显，在大尺寸时甚至比圆柱叶片模型的更大，主要是因为变速度模型中速度在叶片流场中线性减小，微粒由于惯性容易粘附在叶片表面，使层积垢累积率增加，这对大尺寸叶片更为明显。恒定速度模型的层积垢累积率较小，变化较平缓，且其计算公式简单明确。故本文采用平板叶片-恒定速度模型作为叶片积垢的计算模型。

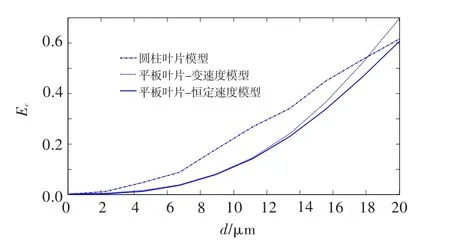
图5 不同微粒尺寸的层积垢累积率分布Fig.5 Distribution of cascade collection efficiencies with various particle sizes

利用恒定速度模型对0 μm≤d≤20 μm尺寸的微粒(图1(a))进行计算，得到不同微粒尺寸分布的层积垢累积率如图6所示。可见case A(P=0.45d+1)的层积垢累积率(平均值)大于其它两种情况，说明大微粒尺寸对积垢率贡献较大。

图6 不同微粒尺寸分布模式的层积垢累积率Fig.6 Cascade collection efficiency of particle distribution patterns with different sizes

6 仿真结果与分析

6.1 叶片积垢沉淀分析

利用平板叶栅-恒定速度模型，以图1(a)中case A作为微粒积垢尺寸分布模式，得到的层积垢累积率随微粒尺寸和叶片特征弦长(c/cref)的变化规律见图7；采用图1(a)中三种积垢微粒尺寸分布模式，得到的层积垢累积率随轴向速度的变化见图8(图中，V/Vref为相对轴向速度)。

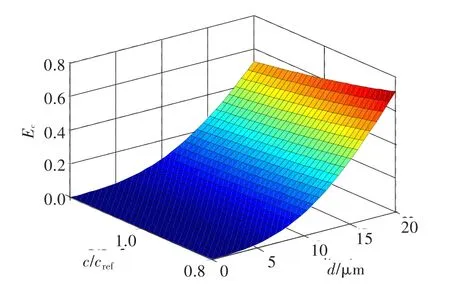
图7 层积垢累积率随叶片弦长和积垢尺寸的分布Fig.7 Distribution of cascade collection efficiencies with various chord length and particle sizes

由图7可知，层积垢累积率随叶片特征弦长的增加而减小，主要是因为微粒在叶片流场中运动时间增长，造成粘附在叶片表面的微粒数量减少所致。从图8中看，层积垢累积率随来流速度的增大而增大，主要是因为速度增大时，微粒经过叶片流场的时间缩短，微粒粘附在叶片表面的数量会相应增加[6]；叶片进口轴向速度越大，叶片上积垢就越多；在case A和case B中，微粒尺寸越大，层积垢累积率增加趋势越明显；但在case C中，微粒尺寸20 μm时，层积垢累积率增长趋势很小，主要因为在对应的积垢尺寸分布模式下，小尺寸微粒占主导，大尺寸微粒数量较小。由此可推知，当大微粒占主导且流动速度较大时，积垢沉淀将非常严重。

6.2 压气机各级积垢量分析

针对压气机各级叶片积垢微粒数目，提出了压气机各级微粒数目相对于第一级积垢数目分布的数学模型。鉴于指数函数具有良好的衰退性质，这里采用指数函数作为积垢微粒数目分布模型。表达式为：

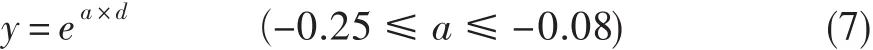
式中：y为微粒数目分布相对量。

利用式(7)得到压气机叶片积垢相对第一级积垢的数目分布，如图9所示。由图可见，级越靠后，叶片上的积垢越少。

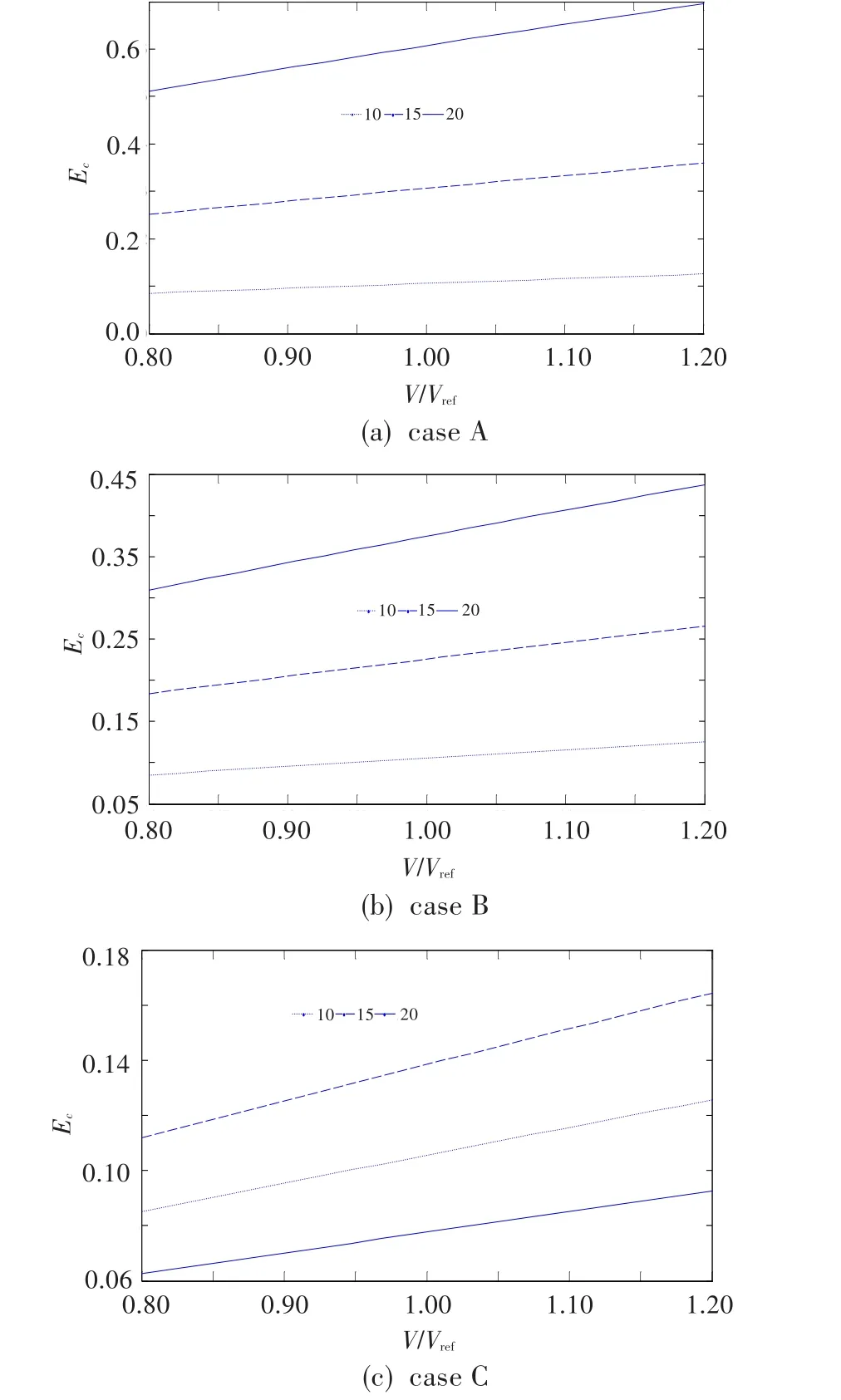
图8 不同积垢微粒尺寸下层积垢累积率随轴向速度的变化Fig.8 Cascade collection efficiencies of particles with different sizes at various axial velocity

图9 压气机各级入口微粒数目分布Fig.9 Incoming particles distribution in compressor stages

利用式(1)和式(7)得到的压气机前5级无因次化积垢质量的分布模式如图10所示。由图中看出，当大尺寸微粒(case A)主导时，大部分大尺寸微粒粘附在前几级叶片上，后几级无因次化质量相对较小。

当小尺寸微粒(case C)占主导时，尽管大尺寸微粒沉积在前几级，但由于其占有的比例很小，所以压气机后几级的无因次化质量相对较大。

图10 无因次化微粒累积质量的分布模式Fig.10 Distribution patterns of the non-dimensional collection mass of particles

6.3 压气机积垢灵敏度分析

从式(5)看出，在ISF的定义式中，压气机级负荷(加功量或压比)愈大、轮毂比愈大，压气机的积垢敏感性就越大，压气机系统对叶片积垢也更敏感。ISF随压比、轮毂比的变化情况如图11所示。

图11 ISF随压比和轮毂比的变化Fig.11 The variation ofISFwith pressure ratio and hub to tip ratio

7 结论

(1)积垢现象与压气机各级的几何尺寸和流动特性关系密切，层积垢累积率随压气机特征弦长的减小而增大，同时随流场中流动速度的增大而增大。

(2)积垢尺寸分布是决定压气机叶片积垢水平的重要因素，大尺寸微粒对层积垢累积率贡献较大。

(3)压气机积垢敏感性反映压气机性能对积垢的敏感程度，压气机压比和轮毂比越大，积垢敏感性越大，压气机性能对叶片积垢越敏感。

[1]Zaita A V，Baley G，Karlsons G.Performance Deteriora⁃tion Modeling in Aircraft Gas Turbine Engines[J].ASME J.Eng.Gas Turbines Power，1998，120：344—349.

[2]王占学，刘增文，叶新农.某型涡扇发动机部件老化对性能影响的分析与计算[J].航空动力学报，2007，22(5)：792—796.

[3]李本威，李冬，沈伟，等.涡轮叶片粗糙度对其性能衰退的影响研究[J].航空计算技术，2009，39(5)：26—29.

[4]李本威，李冬，李姜华，等.单级压气机性能衰退定量研究[J].航空动力学报，2010，25(7)：1588—1594.

[5]Kurz R，Brun K.Degradation in Gas Turbine Systems[J]. ASME J.Eng.Gas Turbines Power，2001，123：70—77.

[6]Song T W，Sohn J L，Kim T S，et al.An Improved Analytic Model to Predict Fouling Phenomena in the Axial Com⁃pressor of Gas Turbine Engines[C]//.Proceeding of the In⁃ternational Gas Turbine Congress.Tokyo，2003.

[7]Trabrin A P，Schurovsky V A.An Analysis of Axial Com⁃pressor Fouling and a Cleaning Method of Their Blading [R].ASME 96-GT-363，1996.

Research of Compressor Blade Fouling Based on Mathematical Model

WANG Guan-chao1，LI Dong2，LIU Xiao-dong3
(1.Aeronautical Military Representatives Office of Navy in Changchun，Changchun 300000；2.Graduate Student Brigade，Naval Aeronautical and Aeronautical University，Yantai 264001；3.Naval Aviation Academy，Huludao 125001)

The mathematic models of compressor blade fouling are compared and analyzed,and the flat-plate cascade constant velocity model is selected as fouling model.The model of fouling distribution at compressor stages is proposed.And the fouling sensitivity is analyzed.Taking the particle of 0～20μm as the research objects,the distribution patterns of the non-dimensional collection mass and cascade collec⁃tion efficiency at different conditions are achieved by simulating the distribution patterns of fouling particle with different sizes.The results indicate that fouling closely relates to the geometric and flow characteristics of the compressor stages,and distribution of different particle sizes is an important parameter to determine the fouling level.It can offer a reference for research on compressor blade fouling.

compressor；fouling；model；cascade collection efficiency；sensitivity

V231.3

A

1672-2620(2012)02-0024-04

2011-05-31；

2012-03-30

王冠超(1984-)，男，天津人，助理工程师，主要从事航空发动机测试与维护技术研究。