涡轮叶片冷却设计优化方法研究

曹志廷，郭文，潘炳华，刘松(中国燃气涡轮研究院，四川成都610500)

涡轮叶片冷却设计优化方法研究

曹志廷，郭文，潘炳华，刘松
(中国燃气涡轮研究院，四川成都610500)

针对某型发动机高压涡轮工作叶片，采用试验设计方法，通过对内腔边界条件的主效应分析，对涡轮叶片截面温度分布进行优化。同时，对影响叶片内腔不同流动与换热类型的冷却结构元件换热系数的几何参数进行敏度分析。最后通过综合优化，获得在原设计基础上的优化结果。结果表明，该方法可以把原设计的截面最大温差有效降低。另外，通过对涡轮叶片冷却设计优化方法的探索，还获得了影响叶片冷却设计结果的参数关系曲线，该方法及结果可在涡轮叶片冷却设计时参考使用。

涡轮叶片；冷却设计；换热系数；试验设计；优化设计

1 引言

随着现代航空发动机对效率和单位推力的不断追求，涡轮进口温度不断提高。目前，航空发动机涡轮进口温度已达2 000 K，远远超出耐高温叶片材料可承受的极限温度，而且随着发动机推重比和性能的不断提高，涡轮前燃气温度还会增加。所以，必须采取有效的冷却方式来降低涡轮叶片的壁面温度。

近年，国外已出现许多新型冷却结构的涡轮叶片，如铸冷、超冷等，但这些技术高度保密，很难获得详细信息。国内对新型冷却结构涡轮叶片的研究多为基础性的(如层板结构等)，所以对常规冷却结构潜力进行深入挖掘(如几何尺寸优化、多腔结构优化、温度分布优化等)，仍有现实意义。由常规冷却结构涡轮叶片构成的冷却系统大多相似，这些内冷结构模式主要为前缘冲击冷却、中部带肋回转通道、尾缘扰流柱排以及与壁面内外相连的气膜冷却等[1，2]。涡轮叶片冷却设计的主要目的，是尽可能合理安排和布局这些冷却结构模式[3]，使得在有限冷气用量下涡轮叶片的壁面温度更低，截面温度分布更合理。

本文在某型涡轮叶片冷却设计的基础上，通过对设计方法的集成和程序自动循环迭代，对叶片冷却设计优化进行初步探索，寻求具有工程实际应用意义的优化结果和方法。

2 涡轮叶片冷却设计优化目标函数的确定

从设计流程看，涡轮叶片冷却设计主要包括：叶片外换热计算、叶片内流计算、叶片气膜修正计算、叶片温度场计算等模块[4]。其中，叶片外换热计算是获得叶片温度场计算时的外边界条件；内流计算，一方面检验内冷结构设计是否合理，同时也为叶片温度场计算提供内边界条件；叶片气膜修正计算是针对有气膜孔的叶片进行的一项修正计算；温度场计算是把内、外边界条件加载到叶片上计算截面温度分布，进一步检验内冷设计是否符合要求，同时其结果可作为温度载荷进行相关的热应力分析等。

在涡轮叶片冷却设计过程中，先进行叶片内冷结构初步设计，然后通过内流计算来检验内冷结构元件冷气参数是否符合相关指标要求(如冷气用量是否超标)，通过温度场计算来检验叶片温度分布是否合理。若不合理，需从头调整相关参数并重新计算，直到各方面均达到相关要求。至此，涡轮叶片冷却设计才算基本完成。所以在冷却用气满足相关要求情况下，最后温度场分布是否合理就成了本阶段检验叶片冷却设计的主要依据。

判断叶片温度场分布是否合理有许多参照指标，如总体温度水平，主要看平均温度和最大温度是否超过相关标准(如材料许用温度)；还有截面最大温差、局部最大温度梯度、特征温度、叶片绝(相)对冷却效果等。由于温度场计算结果还要用于相关的热应力等强度分析，所以比较关心总体温度水平和截面最大温差。本文选择截面最大温差为目标函数，同时参照其它指标。

3 优化设计

优化问题一般可表述为[5]：

式中：SF为规模因子，默认值为1.0；W为权重因子，默认值为1.0；LB和UB分别为设计变量上、下限。

本文以iSIGHT优化软件为平台，以某型发动机高压涡轮转子叶片为计算实例，通过对影响叶片冷却设计结果的各项参数进行循环迭代、分析和比较，获得更为合理的冷却设计结果。

由于涡轮叶片冷却设计过程比较繁复，需要对iSIGHT中集成的设计过程作简化和分段处理。在涡轮叶片冷却设计流程中，最上游和最下游的设计关联性不明显，比如不可能通过改变内冷结构的某一几何参数，就能直接在温度分布中得到及时响应。本文采取分段优化处理。

3.1 涡轮叶片截面温度场优化

在计算涡轮叶片温度时，主要输入参数条件除材料、网格信息等相对不变的参数外，其余为可变的内、外边界条件。边界条件包括边界(环境)温度和边界换热系数，一般不对环境温度作参数优化，只把内边界条件中的换热系数作为设计变量。

在某型发动机高压涡轮转子叶片中截面内边界条件中，其换热系数分布按区域可分为1腔(光滑边和肋边)、2腔(光滑边和肋边)、3腔(光滑边和肋边)、4腔(光滑边和肋边)、5腔(只有光滑边)、绕流柱区段和尾缝区段，见图1。在1腔～4腔中，光滑边和肋边的换热系数相互关联，所以只取一组设计变量。

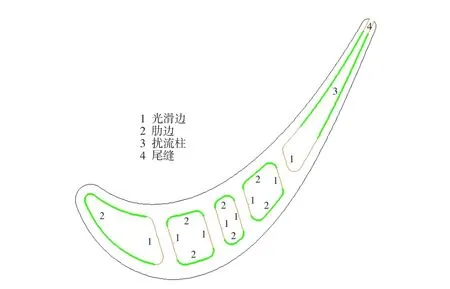
图1 涡轮叶片内腔各区段划分示意图Fig.1 Schemeof the inner boundary divisionsof turbineblade

在温度场优化过程中，以截面最大温差为目标函数，同时也考察其它指标(如平均温度、最高温度等)，以各区段的换热系数为优化设计变量，选取原设计值的±15%为设计变量范围空间。

由于在设计优化过程中，还要进行设计变量的主效应分析，所以在iSIGHT中选取DOE(试验设计)方法。在iSIGHT中建立DOE模型，集成温度场计算过程(本文温度场计算软件为Fluent)，见图2。其中pro组件为设计变量格式载入的预先准备，htc组件为换热系数等全部输入文件的整合，Fluent组件是调用Fluent进行温度场计算，calc组件为读取温度场计算结果后的参数提取。每个组件都有各自的输入和输出过程，同时上个组件的输出也是下个组件的输入。

iSIGHT中DOE模型有7种方法，本文选取默认的LHD(拉丁超立方设计)方法。

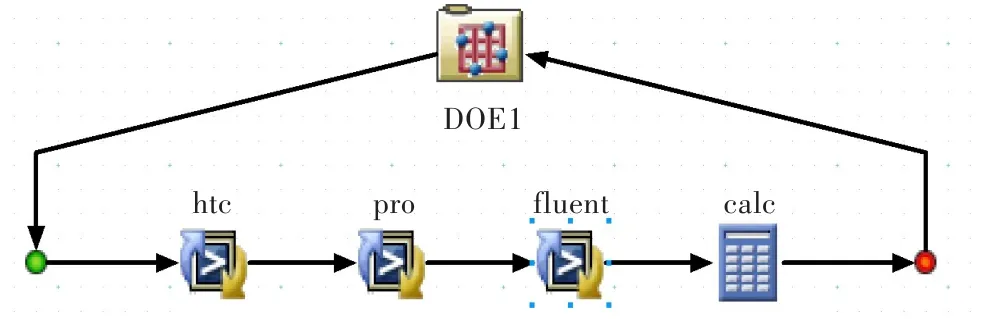
图2 在iSIGHT中对叶片温度分布计算进行优化Fig.2 Optimization of temperature distribution witHiSIGHT

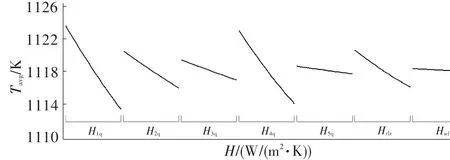
图3 各腔或区段换热系数对截面平均温度的影响Fig.3 Influence ofheat transfer coefficienton area-averaged temperature ofblade sections

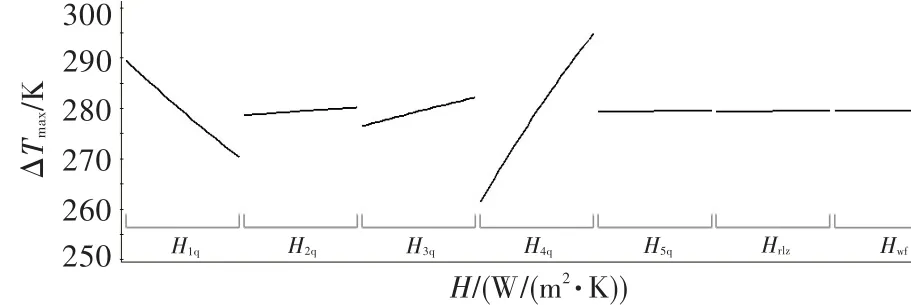
图4 各腔或区段换热系数对截面最大温差的影响Fig.4 Influence ofheat transfer coefficienton themaximum temperature difference ofblade sections

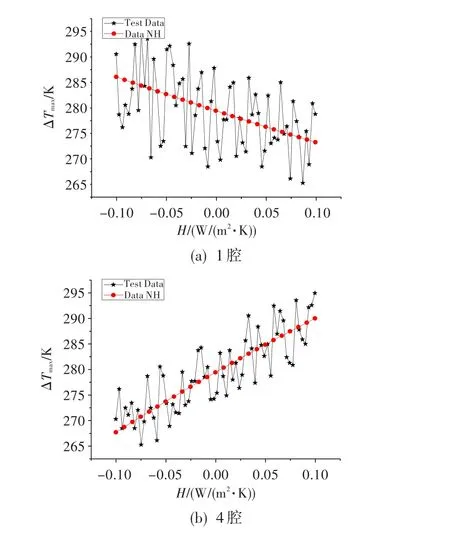
图5 换热系数对截面最大温差的影响Fig.5 Influence ofheat transfer coefficienton themaximum temperature difference ofblade section

表1 温度场优化中的最优、最差值和原设计值对比Table 1 Comparison of the optimum value,theworstvalue and design value of temperature

在设计空间数据抽样中选取试验样本并逐一计算，分别考察各腔或区段换热系数(H)对截面最大温度(Tmax)、平均温度(Tavg)、截面最大温差(ΔTmax)、截面最小温度(Tmin)、截面总体温度(Tzh)的响应，图3、图4列出了部分曲线(多组试验样本的数据拟合)。图中，H1q～H5q分别为1腔～5腔的换热系数，Hrlz、Hwf分别为扰流柱和尾缝的换热系数。

从图中可知，1腔的换热系数对截面最高温度的影响非常大，其响应比较明显，且最高温度随换热系数的增大迅速降低。可见，要想显著降低最高温度，可在1腔作调整，在其它区段效果不明显，这与平常的设计经验完全吻合。在对最大温差的响应上，1腔和4腔的趋势刚好相反。这是因为最高温度出现在1腔，换热系数增大，最高温度降低，截面最大温差也随之降低；最低温度出现在4腔，若换热系数增大，最低温度将进一步减小，截面最大温差反而增大。其它区段中，2腔和3腔小幅上升，5腔、扰流柱、尾缝段趋势不明显。在对平均温度的响应上，各区段都呈下降趋势，只是降幅不一。在对最低温度的响应上，4腔的换热系数最敏感，其它区段幅度很小。总体温度和平均温度的趋势基本一致。上述分布趋势的细节见图5，其中的数据点为多组样本数据，分布趋势为数据点的拟合曲线。

以截面最大温差为目标函数，其中一组优化结果如表1所示。表中，增幅正值表示比原设计值增加，负值表示减少。

在涡轮叶片冷却设计中，常用叶片相对冷却效果ψ作为衡量叶片冷却设计结果的重要指标。其定义[6]为：

式中：Tg为燃气温度；TW为叶片壁面温度，本文用截面平均温度代替；Tc为冷气温度；Tg-TW为绝对冷却效果，在一定程度上反映了叶片的冷却水平。

如果用截面平均温度代替叶片壁面温度，则上式中ψ基本上只与截面平均温度有关。从表1中可见，最差设计值的平均温度反而略低，其绝对冷却效果更好。而实际上1腔温度最高，最差设计是把更多冷气用在其它区域，也能降低平均温度(要消耗更多冷气量)，但这种温度分布(样本数据中极限个例)明显不合理，这也是本文没有把叶片相(绝)对冷却效果作为目标函数进行温度场计算环节优化的原因。如果将上式中的燃气温度用最高温度代替，冷气温度用最低温度代替，可得到另一相对冷却效果(以表示)。可见，最优值把在原值上提高了6.4%，最差值下降了0.5%。

根据表1中数据，若在3腔、4腔和尾缝区段降低相应幅度的换热效果，在其余区段增加相应幅度的换热效果，就能达到或接近最优值，但在实际中不容易实现。对此，将在后续章节中以换热系数值作为目标函数时予以详细分析。

图6为原设计值、最优值的温度场分布，其中Tdit为温差。从图中可看出，最优值比原设计值温度分布更均衡。

3.2 内冷结构参数优化

换热系数是一个综合性很强的参数，与流动状态、流体温度、流经元器件的几何形状等有关。为简化过程，本文只对内冷结构的主要几何参数进行分析，其余参数均沿用原值。在3.1节温度场计算环节的优化分析中，换热系数值按各区段划分给定。在叶片内部流动和换热中，这些区段也刚好对应内流计算网络中的节流元件。由于这些元件各自独立，所以需要对这些元件类型进行单独建模优化分析。本文的叶片算例中，主要对叶身通道、扰流柱、尾缝等节流元件进行优化。

3.2.1 叶身通道换热优化

带肋的叶身通道，其几何参数包括进/出口面积、当量直径、安装角度、周长、肋高、肋间距、光滑边长度、进/出口半径位置、叶片转速等。其中肋高和肋间距有一定可变范围，其余均相对固定。如安装角度一般都垂直流向(90°)，叶片大小和多腔方案决定了进/出口面积、当量直径和周长，进/出口半径位置、叶片转速等参数在气动设计阶段就基本固定。

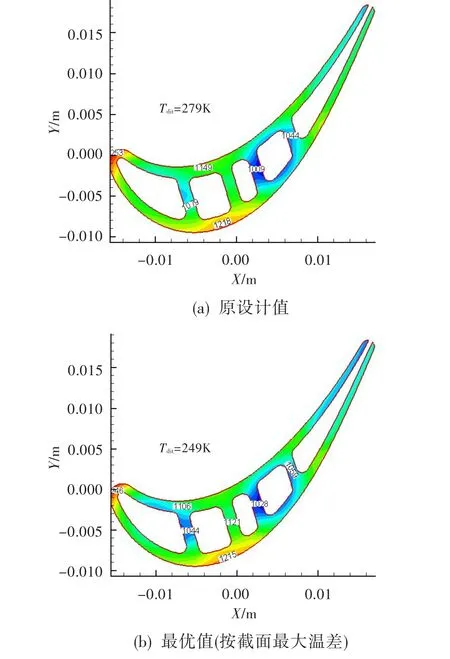
图6 原设计值和最优值的温度分布Fig.6 Temperature distribution ofdesign value and optimum value

对每个变量进行敏度分析(单参数分析，其余变量保持不变)。为了对比，同时也将两个参数同时置于设计空间，考察其相互间的影响(交互效应)。在1腔～4腔均有叶身通道元件，分别建立4组优化模型。

图7为保持肋高不变，肋间距对1腔叶身通道肋边和光滑边换热的影响。可见，肋间距越大，肋边换热系数越小，光滑边换热系数越大。其余各区段的分布规律也相同：肋间距增大，肋扰动减小，导致肋边换热减小；肋间距增大，通道流动阻碍减小，流动增强，导致光滑边换热增强。

肋高和肋间距同时变化时，其相互间有影响，在设计空间中通过数据拟合也可得出相同结论，只是不像单参数分析时的分布规律那样明显(见图8)。

图9为肋高对各腔换热系数的影响(肋间距等其它参数均保持不变，H0为换热系数原值)。从图中不难看出，肋高对各腔肋边换热系数的影响较一致，都单调递增，只是幅度略有差异。但肋高对各腔光滑边换热系数的影响规律明显不同，1腔和4腔先增后减，2腔和3腔持续增加。通常的设计经验是：肋高增大，肋边换热增强，光滑边换热会先增后减。对2腔和3腔的现象，有待今后对设计软件源程序进行深入分析。

图7 肋间距对1腔换热系数的影响(肋高不变)Fig.7 Influence of rib spacing on heat transfer coefficientof chamber 1(fixed rib height)

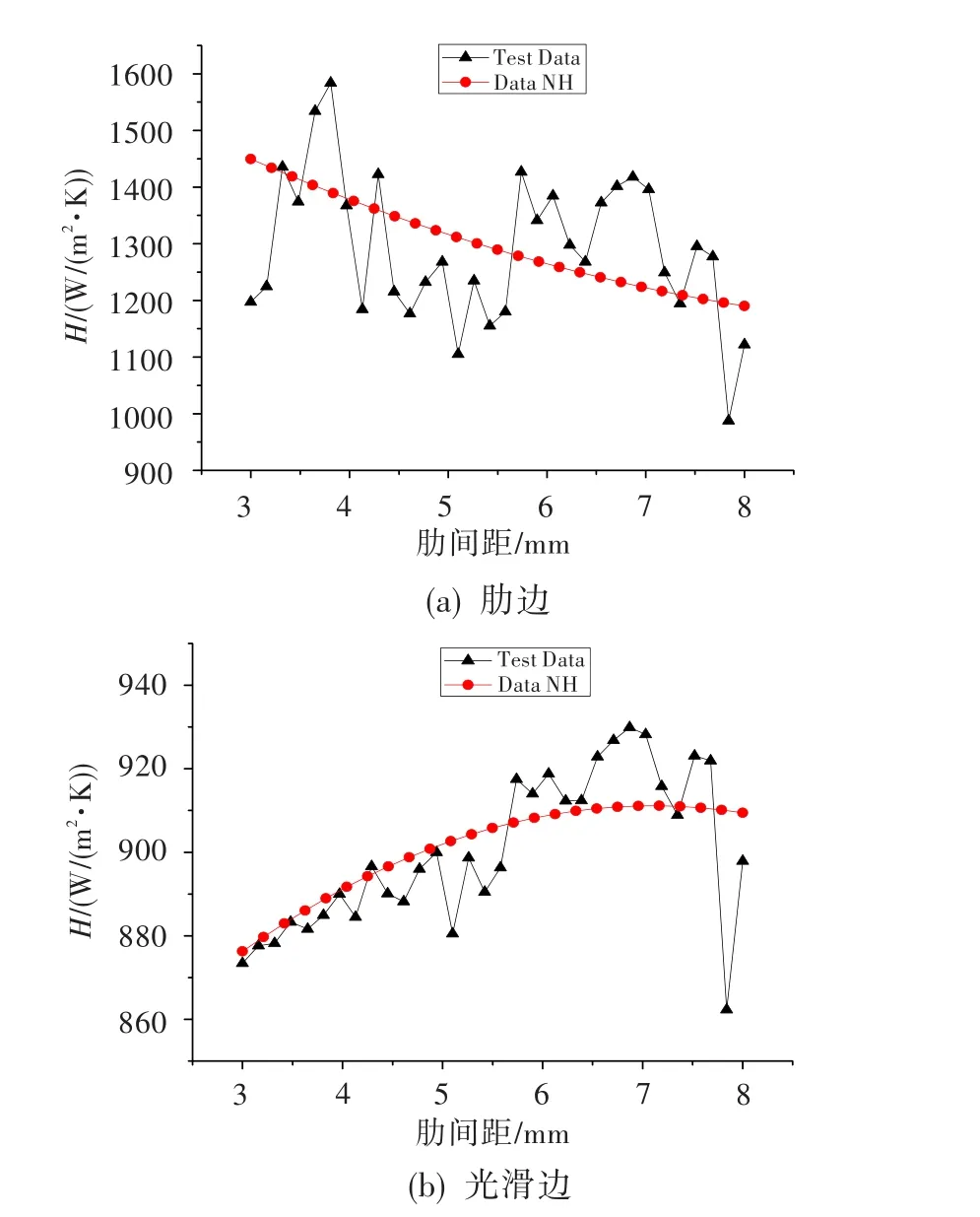
图8 肋间距对2腔换热系数的影响(肋高变化)Fig.8 Influence of rib spacing on heat transfer coefficientof chamber2(variable rib height)

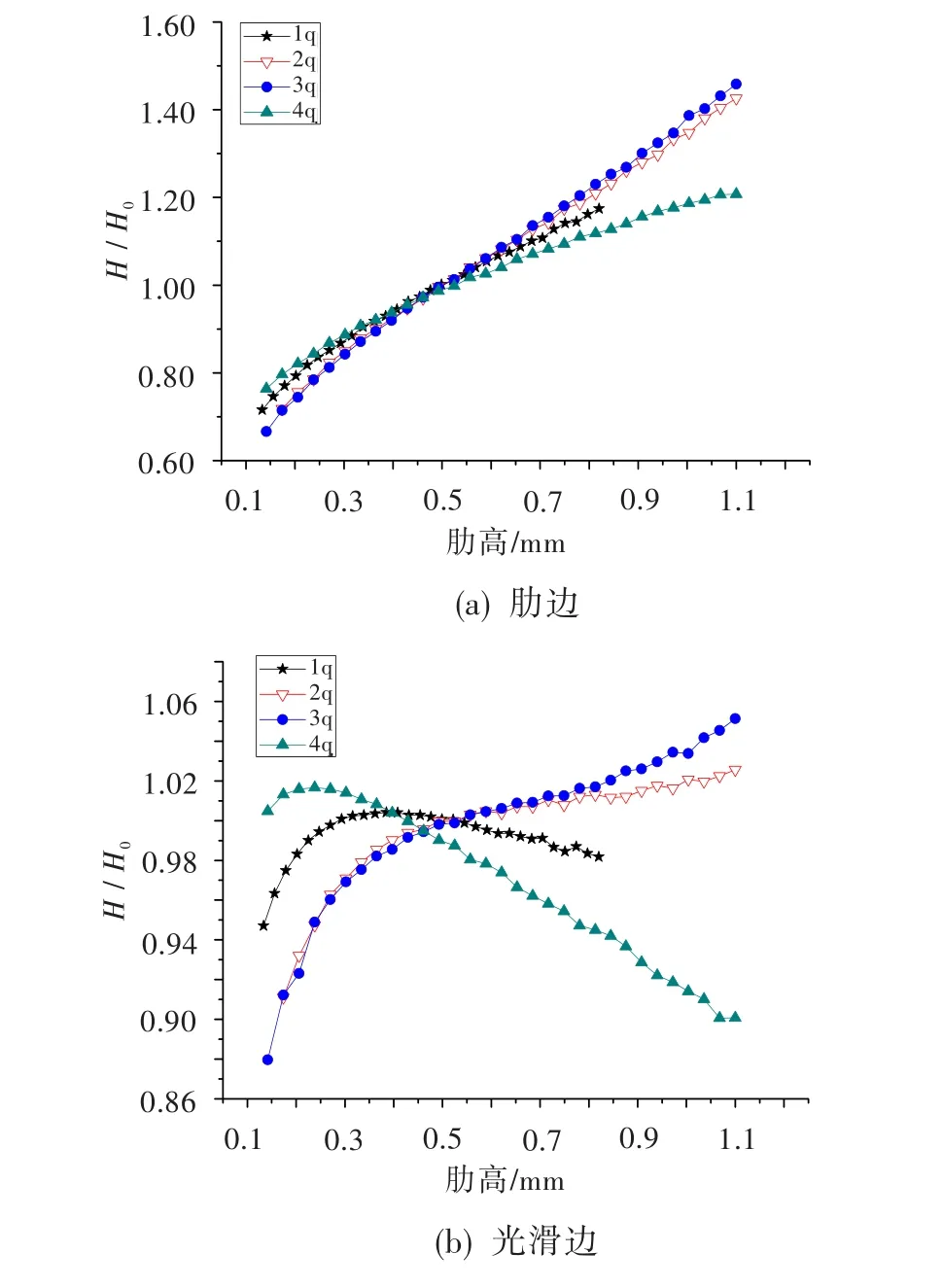
图9 肋高对换热系数的影响(肋间距不变)Fig.9 Influence of rib heighton heat transfer coefficient (fixed rib spacing)

3.1 节中，为使叶片截面最大温差最小，需要1腔换热增加15%、2腔增加5%、3腔和4腔各减小15%。该节中，叶身通道换热系数只设一个变量，另一个变量可通过倍数关系获得，这时肋间距和肋高也保持了固定比例关系(约为10)。此处为深入分析，将肋边换热系数和光滑边换热系数作为两个设计变量，而且若以肋间距和肋高为设计变量对叶身通道换热系数进行寻优，发现最优值也在肋间距与肋高10倍关系附近，与原设计值的10倍关系吻合，即原设计值几乎就是最优值。但从3.1节结果看，3腔和4腔并不需要达到最优值。

3.2.2 扰流柱元件换热优化

叶片内流计算网络中，扰流柱元件的几何参数包括进/出口面积、扰流柱直径、长度、扰流柱流向间距、扰流柱切向间距、沿流向排数、扰流柱数量、进/出口半径位置、叶片转速等。

在iSIGHT中对设计变量进行敏度分析(设计变量保持1个，其余参数不变)，分别考察扰流柱直径、流向间距、切向间距、长度、扰流柱沿流向排数、扰流柱数量等参数对目标函数(换热系数)的影响，部分曲线如图10所示。从图中可看出，扰流柱直径和扰流柱切向间距对扰流柱的换热是一个分段函数。在这些几何参数中，扰流柱直径、切向间距、流向间距相互影响，其余参数相对独立、变化范围有限，所以以这三个参数为关键设计变量进行优化。在iSIGHT中建立优化组件模型，选择默认的NLPQL(序列二次规划法)，对各自变量空间给出上、下限加以约束，设定目标函数，进行优化计算，结果见图11。

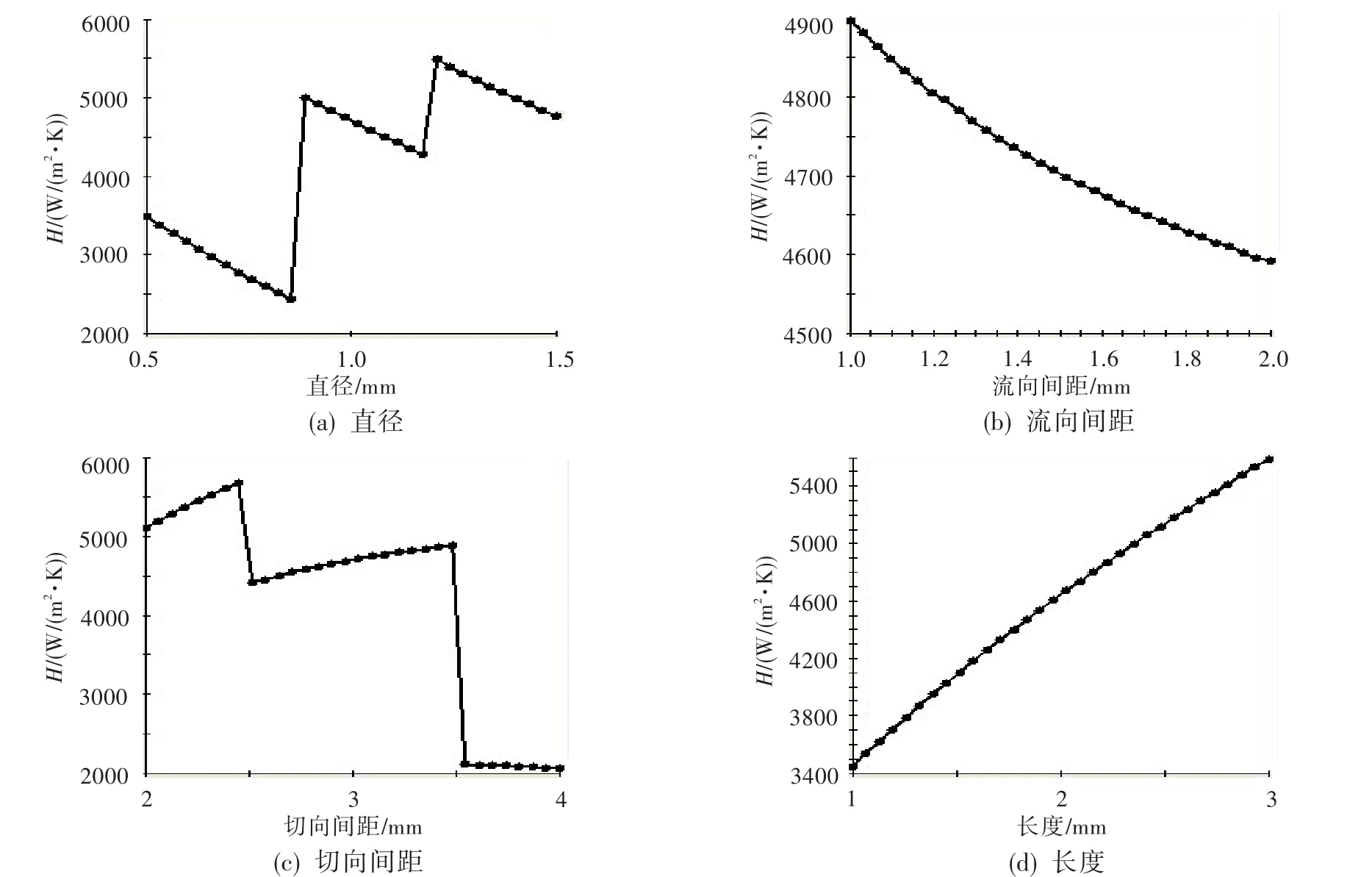
图10 扰流柱内冷结构参数对换热系数的影响Fig.10 Influence of pin fin parameterson heat transfer coefficient

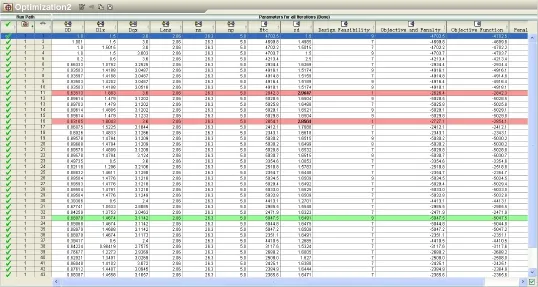
图11 扰流柱内冷结构参数优化结果Fig.11Optimized resultsof pin fin parameters

表2 扰流柱内冷结构参数优化结果与原值的比较Table 2 Comparison between optimized resultsof pin fin parametersand original value

表3 温度场计算环节再次优化中的最优值和原设计值比较Table 3 Comparison between the optimum value in temperature re-optimization and design value

表2为从优化结果提取的相关参数与原设计值的比较。可见，对扰流柱三个几何参数稍微进行调整，就能使目标函数——扰流柱换热系数提高7.3%。但在实际设计中，需综合考量扰流柱直径较细时的强度问题。

3.2.3 尾缝元件换热优化

尾缝元件换热，其所关联的几何参数主要有面积、尾缝宽度和长度，其中尾缝长度只参与流量系数计算。实际设计中，参照经验做法，流量系数为预先给定的常数，尾缝长度不参与计算。

在iSIGHT中对面积和尾缝宽度各自进行一定空间范围的计算分析，结果表明，它们对尾缝元件的换热系数都呈递减关系。

实际设计中，由于叶片尾缘厚度有限，在有限厚度中开缝更加困难，所以尾缝宽度也基本固定。因此，尾缝元件换热主要考虑尾缝面积。需注意，尽管减小尾缝面积可增大尾缝元件换热强度，但减小尾缝面积是在尾缝沿叶身高度上堵住一段来实现的，这样会大大减少其它区域的尾缝换热面积，对整个叶身通过尾缝冷气带走热量不利，而且也会造成有些区域无尾缝的情况。3.1节中，为达到温度场截面温差最小，要求尾缝区段的换热系数降低5%，尽管这个目标可以达到，但应综合考虑整个叶身的换热。

3.3 温度场计算的再次寻优

考察上述内冷结构参数对各区段换热的影响，发现有些区段不能满足3.1节中的设计空间范围，所以需要对各区段换热系数的变化空间进行重新调整，即1腔～5腔只减不增，扰流柱区段0～7.3%，尾缝区段不变。在iSIGHT中重新调整设计空间，并再次进行寻优计算，其结果如表3所示。从表中可以看出，截面最大温差比原设计值降低了5.1%。

4 结束语

通过iSIGHT平台对涡轮叶片冷却设计进行了优化方法探索。由于涡轮叶片冷却设计的复杂性及设计中流程的关联程度，本文采取分段优化方法，在温度场计算和叶片内冷结构参数设计环节分别寻优，然后综合考虑，最终得到最优值及寻优的方法和思路。

同时还间接验证了原设计值的合理性(尽管某些环节不是最优，但与最优值比较接近)，得到了涡轮叶片冷却设计过程中部分设计变量对设计结果的影响规律，可为涡轮叶片冷却设计提供参考。

[1]顾维藻，涂建平，刘文艳，等.燃气轮机涡轮叶片冷却通道内的流动与传热研究[J].工程热物理学报，1996，17 (3)：323—327.

[2]Manna M，Raffaele T.Optimum Aero-Thermal Design of Turbomachinery Blading Systems Accounting for Variable Operating Conditions[R].ASME 2003-GT-38629，2003.

[3]虞跨海，岳珠峰，杨茜.涡轮冷却叶片气动与传热设计优化[J].计算力学学报，2010，27(2)：139—143.

[4]航空发动机设计手册总编委会.航空发动机设计手册：第16册——空气系统及传热分析[K]．北京：航空工业出版社，2001.

[5]Van der Velden A.iSIGHT-FD,a Tool for Multi-Objec⁃tive Data Analysis[R].AIAA 2008-5988，2008.

[6]Faulkner F E.A Nalytical Investigation of Chord Size and Cooling Methods on Turbine Blade Cooling Requirements [R].NASA CR-120882-Book 1，1971.

Optim ization of Turbine Blade Cooling Design witHiSIGHT

CAO Zhi-ting，GUOWen，PAN Bing-hua，LIU Song
(China Gas Turbine Establishment，Chengdu 610500，China)

Based on the established turbine blade parametricmodel,this article chose iSIGHT to optimize the temperature field of turbine blade using inner boundary conditions and to optimize heat transfer coeffi⁃cient of the structure component using geometry parameters.It successfully reduced themaximum tempera⁃ture difference of blade section by thismethod.This researcHshows some relationships among different pa⁃rameters,and would be referential for turbine blade cooling design.

turbine blade；cooling design；heat transfer coefficient；design ofexperiment；optimization design

V233.5；V232

A

1672-2620(2012)04-0030-07

2011-12-26；

2012-10-17

曹志廷(1972-)，男，四川万源人，高级工程师，硕士，主要从事航空发动机空气系统与热分析工作。