基于幂律分布的网络用户快速排序算法
2012-06-29张宏莉张伟哲
张 玥,张宏莉,张伟哲
(哈尔滨工业大学 计算机科学与技术学院,黑龙江 哈尔滨 150001)
1 引言
随着Web2.0的兴起,计算机网络将用户从传统的信息接收者转变为信息制造者,网络论坛、博客、微博作为新兴媒体对传统媒体产生了极大冲击,以前的社会影响主要由传统媒体决定和控制,但新兴媒体下用户发布的一条信息就可能引发蝴蝶效应,从天涯网络论坛中大量长期的对“药家鑫”事件的讨论到“郭美美”的炫富微博,无不显示出网络用户在新兴媒体中“草根”阶层对社会发展的积极影响。如何评价新兴媒体中用户的影响力是近年来社会网络研究中的一个重要内容,文献[1]分析博客中用户影响力,文献[2-7]分析微博中用户影响力,用户影响力计算主要根据用户的活跃性和受众性以及发布的内容,对社会网络中的用户进行排序。文献[8-10]量化了社会网络中存在的影响力。文献[11-12]对主题进行区分量化了主题级用户影响力。针对大规模数据下影响力计算困难性,文献[11]采用分布式框架在Map-Reduce上量化影响力强度。
用户影响力计算结果与对影响力的定义和分析有很大关系,文献[4,7]中比较多种影响力计算方法,均认为影响力值由计算方法决定。文献[4]比较了twitter中利用粉丝数、依据粉线关系所形成的网络拓扑采用Pagerank算法[13]、回复数三种方法的排序比较,前两种方法都是反映了twitter用户在twitter空间中的被认识程度,该影响力是其综合表现和社会传播的结果,前两种方法结果相似,但没有明确反映出其内容影响力,后者与前两者结果不同,而依据回复数的排序结果仅部分反映了内容影响力而未考虑到传播的影响[1]。网络用户产生影响过程也是信息扩散过程,从信息扩散角度研究影响力包括文献[14-15]等,文献[14]分析博客空间中的链接模式,文献[15]计算具有最在化影响力的少量用户。博客、微博和网络论坛信息传播方式不同,博客、微博是根据用户信息定制的定向推送式传播;网络论坛是公开的大众用户讨论场所,基于服务器的集中式讨论,网络论坛中信息全部用户可见。
早期应用于Google搜索引擎的网页排序算法Pagerank[1]利用网页间链接关系构造有向关联图,依据随机游走和关联图的排序算法,网页间的指向关系是网页分值的主要依据。Pagerank算法设计思想也适用于网络论坛中: 论坛中用户A回复了用户B是基于人主观判断后对B的一种认同表现,因此我们认为B对A产生了影响,而且论坛中主题内用户自然形成基于话题的社区。由此可根据主题内用户间回复关系,构造用户关联图,应用Pagerank算法排序网络用户。但Pagerank算法没有深入分析节点度分布,该算法运行效率有提高空间。本文的研究问题。主要针对大规模的社会网络数据,在对用户复杂排序应用中如何提高数据的存储和运行效率。本文在网络论坛中用户度分布符合幂律特性,对Pagerank算法依据度分布进行数据结构优化,按入度和出度进行集合划分,采用链表数据结构,实现基于集合划分的快速排序算法SD-Rank。在天涯论坛上的用户排序实验中,算法时空复杂性大大降低。
2 相关工作
1) Pagerank算法
经典的网页排序算法包括Pagerank算法[16]和HITS算法[17]。Pagerank算法根据页面间指向关系迭代计算页面的排序值,被大量指向的页面其排序值高,排序值高的网页所指向的页面排序值也高,具有互增强特性;Pagerank算法还引入了随机游走机制,即每次以一定的概率随机选择节点以防止进入连通子图中。Pagerank算法可表示为式(1):
A是网页间关联矩阵,X是Pagerank迭代向量,X(0)是初始随机游走向量,s是阻尼系数,1-s为随机游走参数。归一化后,网页排序值最后收敛于特征值为1对应的主特征向量,与X(0)无关,但X(0)影响算法迭代速度。
2) Pagerank改进快速算法
提高Pagerank算法运算速度主要从算法和数据两个角度,文献[18]总结了Pagerank算法的本质: 节点rank值主要取决于连接该节点的边,且在边上仅传递rank值。文献[18]加速计算方法: a)减少迭代次数法[19]。在计算排序值的收敛向量时,Pagerank的Power算法迭代次数取决于所选取的初始值X(0)。改进算法: 迭代过程中修改迭代向量,令X(i+1)=X(i)+Z(i)使其快速逼近主特征向量,且迭代过程中利用启发式修正Z向量;b)划分数据。按节点间连通性划分为多个连通区域[9],单遍迭代过程中,在节点间连接稠密区域可连续计算几次再进入下一连通区域继续;c)减少计算量。当节点间关联图随时间变化时,若关联图变化不大可采用前一次rank结果作为启发式来快速排序,当节点rank值稳定时不必进行下轮迭代,仅对未收敛于稳定概率分布的节点进行迭代以减少计算量。
3) 本文思想
Pagerank算法本质思想为在关联网络中以一定概率随机选择节点,然后在该节点沿出边向外游走,节点rank值主要取决于连接该节点的边,且在边上仅传递rank值,该思想也适用于网络用户的影响力计算,但本文不同于文献[18-19],基于大量节点入度为0特点,对入度为0集合进行优化处理以减少存储和运输复杂度。本文与上述Pagerank加速算法不同之处在于,基于网络论坛中80%以上用户入度为0的数据特征,提出基于入度是否为0进行集合划分来加速pagerank算法,而该数据特征和文献[9]基于集合划分思想一致。入度为0节点为论坛中仅发表评论,没有引发别人评论的用户,这类用户对论坛的影响仅增加了帖子数量而没有产生交互性影响,用户实质性影响表现为发表主题以及在主题中发表见解并引发正负面争论。
3 网络用户快速排序算法
3.1 矩阵与图的稀疏性
对于一个n×n矩阵,其存储空间为n2。一个n阶方阵与一个n维列向量相乘,运算复杂度为O(n2)(需要n*(n个乘法+(n-1)个加法))。当n数量级较大时存储运算开销都较大。当n×n矩阵中多数值为0时,为稀疏矩阵[20]。
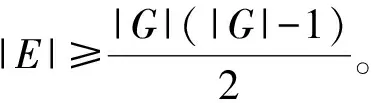
3.2 关联图的邻接表表示
稀疏图可用邻接表表示,如图1所示。用邻接表形式表示存储空间小且计算复杂度低[21]。有向图G=(V,E)可表示为一个包含|V|个链表的数组Adj。∀u,v∈V,(u,v)∈E,则v在u的邻接表中。图G的邻接表所需存储空间为Θ(V+E)。
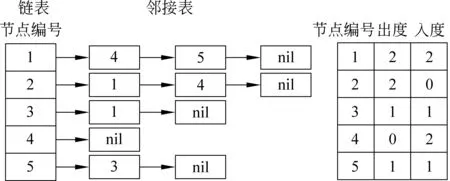
图1 用户关联图所对应的邻接表表示
3.3 基于邻接表的Pagerank计算
根据Pagerank算法(式1),图G=(V,E)中节点v的rank值由两部分而来。
1) 当边(u,v)∈E时,u的rank值rank[u]沿关联矩阵游走,乘以因子s后按其出度均分到u所指向的节点,故v的rank值从指向其的节点u处传播而来。当多个点u1,u2,…,uk都指向v时,(u1,v)∈E,(u2,v)∈E,(u3,v)∈E,…(uk,v)∈E,Rank[v]=∑rank[ui]*s/out[ui]
2) 每个节点随机游走所分的rank值,每个节点都乘以系数(1-s)后均分到所有节点:
Rank[v]=(1-s)*∑(u∈G)rank[u]/n
Rank计算过程见算法1。
算法1基于链表方式的排序算法
Input (链表B,初始rank向量A0,出度向量out,阻尼系数s)
A1:迭代过程保存rank值向量,初始全0,,n节点数
A2: 上一次迭代rank向量,初始全0,e:rank向量收敛误差,k迭代次数
function pagerank-iterate-computation(L,A0)
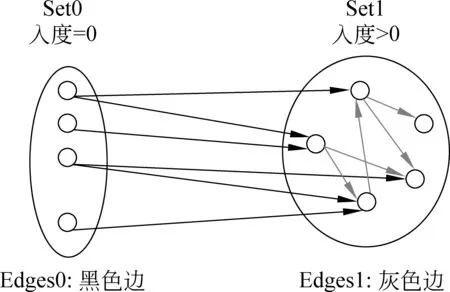
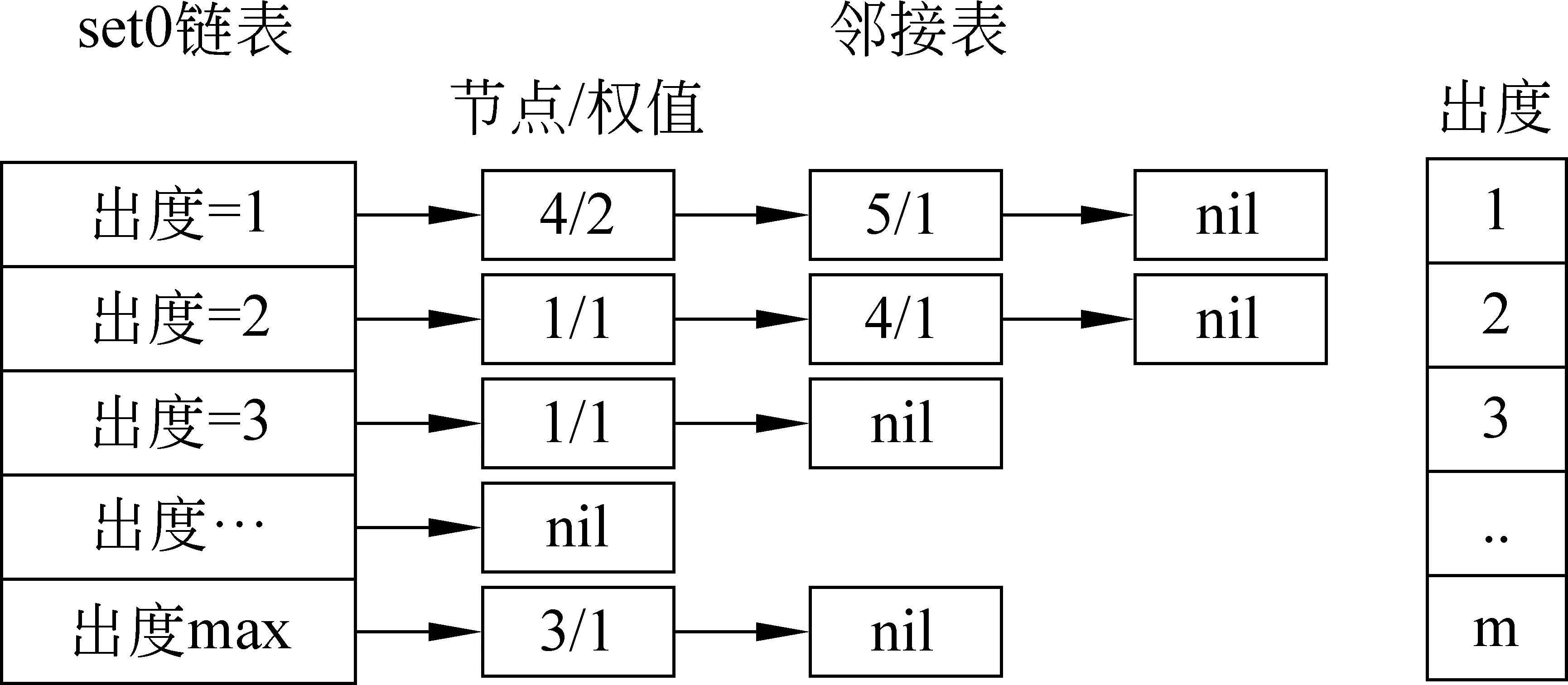
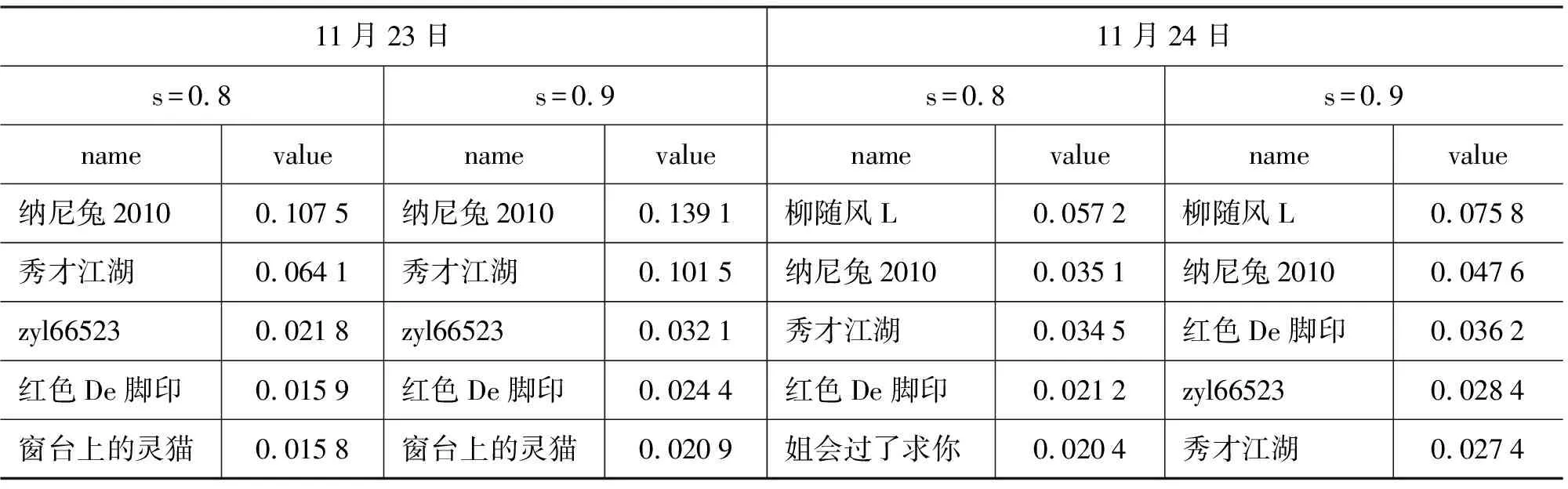
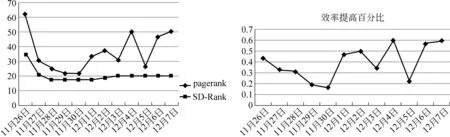
1 while (||A0-A2||2 2 { rank=0; A2=A1; 3 For (i=1 , i++, i<=n) rank=rank+ A0[i]; 4 For (i=1 , i++, i<=n) A1[i]=rank*(1-s)/n; 5 For (count=0;count++;count 6 { While (当B[count]链表未考察结束) //边数 7 { read j //(i,j)?E 8 A1[j]= A1[j]+A1[count]′s/out[count]; 9 } 10 } 11 A0=A1; 12 } Output A0 算法2基于SD-Rank的集合部分排序算法 Compute-rank-b0 计算b0桶中rank值的分配 { 1 max-out=1; //出度最大值 2 For (A[v]=w) //对B0中节点v的邻接表按出度放入相应的桶中 3 { i=out[v]; 4 Insert List v into B0[i]; //插入排序,排序时计算节点出现次数 5 If (i>max-out ) max-out=i; 6 } 7 For(i=1 to max-out) 8 { while list B0[i] is not null 9 { read 节点j and weight[j]; 10 A1[j]= A1[j]+A0[k]′s′weight[j]/i; //节点k入度=0 } } 定义1: 入度为0的点所构成的集合称为set0;入度大于0的点所构成的集合称为set1。 定义2: 由入度为0的点所引发的边的集合为edges0。其他边的集合为edges1。edges0集合即由set0中节点指向set1中节点所构成的边。edges1集合即由set1集合内部节点间关联所构成的边。 性质1点集合set0和set1不相交,且点的总集由set0和set1构成,setV=set0∪set1。 性质2边集合edges0和edges1不相交,且edgesE=edges0∪edges1。 关联图的点集合和边集合划分后如图2所示。set1集合中节点影响力值: 1)由随机游走;2)由集合内部相互指向得到;3)由集合0节点指向得到。 图2 关联图基于入度的集合划分 3.4.1 集合划分后进行优化 Set0中节点入度为0,若其初始rank值相同,出度相同时其向外传播的rank值也相同,按出度值重新划分桶,那么链接表中数组B的元素数降低到set0的出度数。Set0中出度相同的节点指向相同节点时,累计指向节点出现次数,邻接表采用加权表示,如图3所示。集合划分可采用对节点着色法表示,set0集合用w表示;set1点颜色为用b表示。对set0集合引发的edges0边集合,应用加权邻接表表示后的rank计算过程见算法2。 图3 入度为0的节点加权邻接表表示 3.4.2 运算复杂性分析 对B0链表的运算复杂度分析:Compute-rank-b0的第二行对B0中节点进行处理,循环了count_b0次;第四行采用插入排序法链接到第i个桶,最少插入i次,最多插入count_b1次;第7行循环了max-out次;第八行同第四行。运算复杂度 令c=count_b1 对T(n)等式两边取数学期望,有 令Xij=I{A[j]落入桶i中},i∈[1,max-out],j∈[1,c]。 对B0桶进行改进后,运算复杂度下降到Θ(count_b1)。count_b1为入度不为0用户数量。即: 对入度为0节点按其出度值划分桶后其运行复杂度为Θ(|set1|)。 天涯网络论坛是中国门户网络论坛,用户活跃,内容广泛,部分主题讨论深入交互性好。实验数据集采集自天涯网络论坛天涯杂谈版块,采用工具为实验室开发的爬虫软件,于2010年12月21日按主题进行广度爬行。过滤掉回复数少于50的主题。抽取了11月26日到12月7日共12天的数据进行了测试。数据按天划分,提取出用户间回复关系,默认情况下回复给主题创建者。统计结果如表1所示。 表1 数据集统计 统计11月26日到12月7日的入度为0用户数及所占比例,如图4所示。图4左为日入度为0和出度为1用户数量,图4右为日入度为0和出度为1用户占总数比例。平均日入度为0用户数5 566。入度为0用户占总人数日平均比例为86.16%。出度为1用户数日平均4 430人。出度为1用户占总人数日平均比例为64.98%。 图4 入度为0和出度为1日用户数统计及相对比例 选取11月23日作为样本点,统计入度和入度的频数、出度和出度的频数。图5为用户入度频数、出度频数对数坐标图,由图可看出入度、出度符合幂律分布。文献[22-23]分析了web入度符合幂律分布,web入度为k的概率与1/ka(2 图5 11月23日度对数对数分布图 图6 比较两种算法排序结果相似性 为考察SD-Rank算法和Pagerank算法排序结果的相似性,采用Kendall’s tau排序相关性比较的改进公式[4,25-26]比较排序结果差异,Kendall’s tau公式为: 0≤K≤1,K=0表示R1和R2排序结果完全不同,K=1表示R1和R2排序结果完全相同。 图6所示为Kendall’s tau排序相似性比较结果,K值在0.7以上,说明SD-Rank与Pagerank排序结果相似性大。表2为用户排序结果top5明细,两种算法top5结果相同。 表2 11月23-24日排序top5用户结果 比较运行Pagerank和SD-Rank算法的运行时间。运行时间对比如图7左所示提高4-30s。运行效率提高比例如图7右所示。SD-Rank算法运行效率平均提高了39%。 图7 算法运行时间和SD-Rank提高效率 本文以网络论坛为用户排序应用背景,提取用户关联图。基于用户度符合幂律分布,改进Page-rank 算法,将用户划分为入度是否为0的两个集合。对入度为0的用户集合,再按出度构造链接表,采用加权链接数据结构。基于度分布进行集合划分,加权链接结构的SD-Rank算法,时空复杂度降低为O(V′),V′为入度不为0节点集合,大大降低了排序的存储空间和运行效率。 [1] Agarwal N., Liu H., Tang L., et al. Identifying the influential bloggers in a community[C]//Proceedings of the international conference on Web search and web datamining(ICWSM ’08),New York, US, ACM, 2008:207-218. [2] Paul N. Bennett, Krysta Svore, Susan T. Dumais.Classification-enhanced Ranking[C]//Proceedings of the 19th international conference on World Wide Web, Raleigh, NC, USA, 2010:111-120. [3] T. L. Fond, J. Neville. Randomization Tests for Distinguishing Social Influence and Homophily Effects[C]//Proceedings of the 19th international conference on World Wide Web, Raleigh, NC,USA, 2010:601-610. [4] H. Kwak, C. Lee, H. Park, et al. What is Twitter, a Social Network or a News Media[C]//Proceedings of the 19th international conference on World Wide Web, Raleigh, NC, USA, 2010:591-600. [5] S. Wu, J. M. Hofman, W. A. Mason, et al. Who says What to Whom on Twitter[C]//Proceedings of the 20th international conference on World Wide Web, Madrid, India, 2011:705-714. [6] M. Cha, H. Haddadi, F. Benevenuto, e al. Measuring user influence on wtitter: The million follower fallacy[C]//Proceedings of the 4th International AAAI Conference on Weblogs and Social Media, Washington DC, 2010. [7] J. Weng, E. P. Lim, J. Jiang, et al. Twitterrank: finding topic-sensitive influential twitterers[C]//Proceedings of the 4th ACM international conference on Web search and data mining(WSDM), 2010:261-270. [8] Dan Cosley, D. Huttenlocher,Jon Kleinberg,et al. Sequential Influence Models in Social Networks[C]//Proceedings of the International Conference on Weblogs and Social Media(ICWSM), 2010. [9] A. Anagnostopoulos, R.Kumar, M. Mahdian. Influence and correlation in social networks[C]//Proceedings of the 14th ACM SIGKDD international conference on knowledge discovery and data mining,2008:7-15. [10] P. Singla, M. Richardson. Yes, there is a correlation: from social networks to personal behavior on the web[C]//Proceedings of the 17th international conference on World Wide Web, 2008:655-664. [11] Jie Tang, Jimeng Sun, Chi Wang, et al. Social Influence Analysis in Large-scale Networks[C]//Proceedings of the 15th ACM SIGKDD international conference on knowledge discovery and data mining. ACM, 2009:721-730. [12] Aditya Pai, Scott Counts. Identifying Topical Authorities in Microblogs[C]//Proceedings of the fourth ACM international conference on Web search and data mining(WSDM ), 2011:45-54. [13] J. Leskovec, E. Horvitz. Planetary-scale views on a large instant-mssaging network[C]//Proceedings of the 17th international conference on World Wide Web. Beijing, China, 2008:915-924. [14] D. Kemp, J.Kleinberg, E. Tardos. Maximizing the spread of influence through a social network[C]//Proceedings of the 9th ACM SIGKDD international conference on knowledge discovery and data mining, 2003:137-146. [15] S Brin. L Page, R Motwani, T Winograd. The pagerank citation ranking: Bringing order to the web[R]. Technical report, Stanford University, 1999. [16] J Kleinberg. Authoritative sources in a hyperlinked environment[J]. Journal of the ACM, 1999,46(5):604-632 [17] Frank Mcsherry. A uniform Approach to Accelerated Pagerank Computation[C]//Proceedings of the 14th international conference on WWW, 2005:575-582. [18] Sepandar D. Kamvar, T H. Haveliwala, C D. Manning, et al. Extrapolation Methods for Accelerating Pagerank[C]//Proceedings of the 12th international conference on WWW, 2003:261-270. [19] Stoer Josef, R. Bulirsch. Introduction to Numerical Analysis[M]. Berlin, Dover Publications. 2002: 619 [20] Thomas A. Smith. The web of law[J]. San Diego Law Review,2007,44(309). [21] A. Broder, R. Kumar, F. Maghoul, et al. Graph structure in the Web[C]//Proceedings of the 9th International World Wide Web Conference, 2000:309-320. [22] David Easley, Jon Kleinberg. Networks, Crowds, and Markets: Reasoning about a Highly Connected World[M]. Cambridge University Press, 2010. P546 [23] R. Fagin, R.Kumar, D. Sivakumar. Comparing top k lists[C]//Proceedings of the 14th annual ACM-SIAM symposium on discrete algorithms,2003:28-36. [24] F. McCown, M. L. Nelson. Agreeing to disagree: search engines and their public interfaces[C]//Proceedings of the 7th ACM/IEEE-CS joint conference on digital libraries. ACM,2007:309-318. [25] Thomas H. Cormen, Charles E.Leiserson, Ronald L. Rivest, et al. Introduction to Algorithms[M]. The MIT Press.2001. P527 [26] N. Agrawal, H. Liu, L. Tang, et al. Identifying the Influential Bloggers in a Community[C]//Proceedings of the international conference on Web search and web data mining(WSDM’08), 2008:207-218.3.4 基于集合划分的SD-rank改进算法

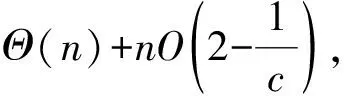
4 实验结果
4.1 数据描述

4.2 入度和出度统计结果
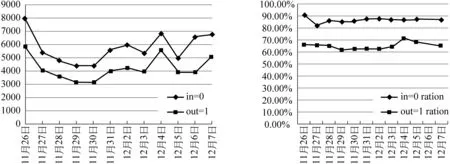
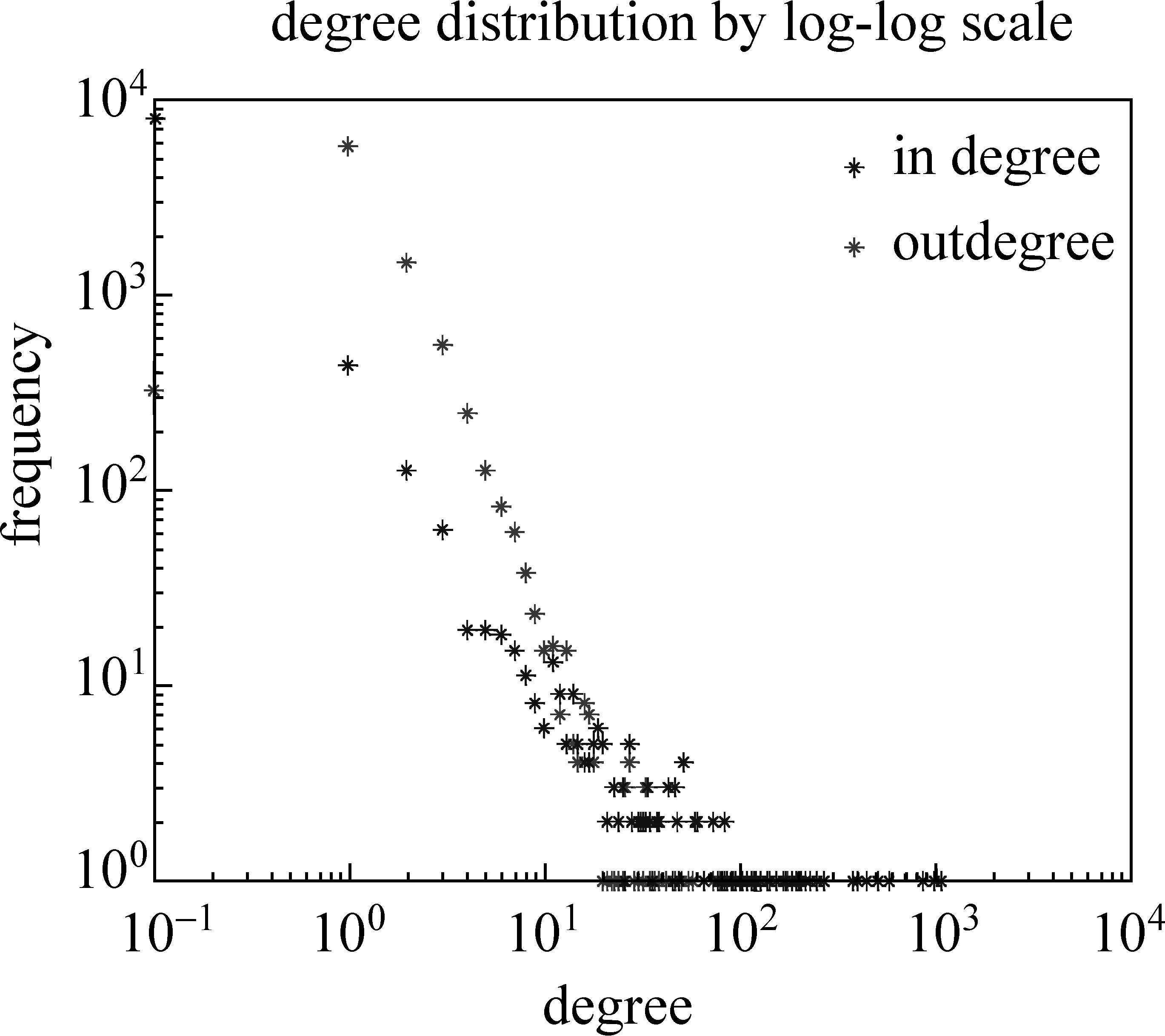
4.3 SD-Rank算法和Pagerank算法运行结果比较
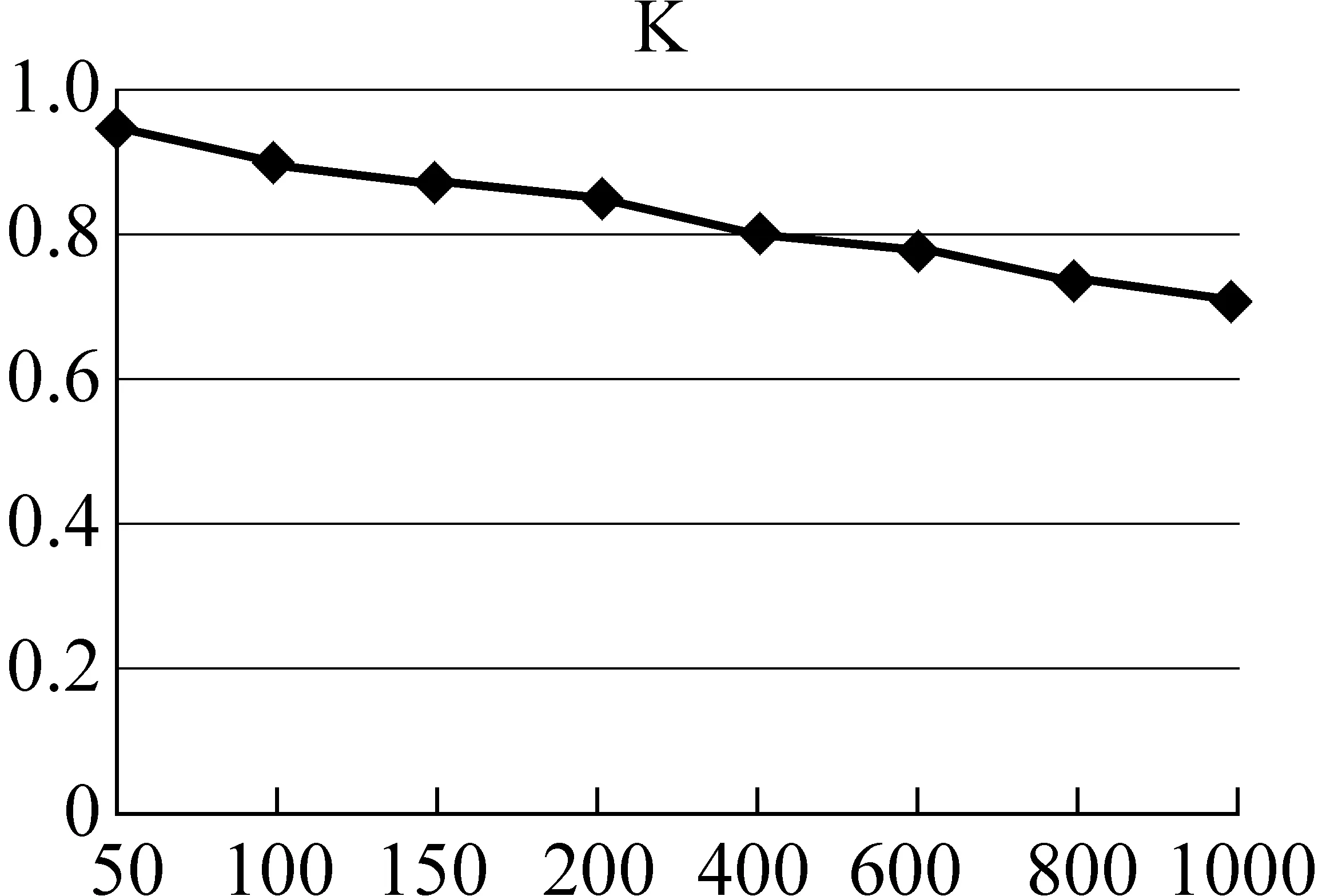
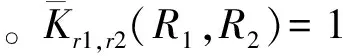
4.4 SD-Rank算法运行效率
5 结论
