马尾松主要蛀干害虫林间诱捕序列的似乎不相关分析

陈绘画 张汝忠

(浙江省仙居县林业局，仙居，317300)

徐志宏

(浙江农林大学)

松墨天牛(Monochamus alternatus Hope)、短角幽天牛(Spondylis buprestoides(L.))等是我国马尾松(Pinus massoniana)林的主要钻蛀害虫，同时还能携带松材线虫［1］，尤其是松墨天牛为我国松材线虫病最重要的传播媒介。由于蛀干类害虫成虫体壁及鞘翅坚厚、耐药力较强、羽化期不整齐，在日本人发现从松树伐倒木上收集的挥发性物质对松墨天牛成虫具有强烈的引诱作用后［2－5］，用引诱剂诱杀蛀干类害虫的方法便得到较快地推广［6－8］。蛀干类害虫引诱剂在诱杀林间松墨天牛、短角幽天牛、立毛角胫象(Shirahoshizo erectus Chen)和松瘤象(Hyposipalus gigas Linnaeus)等松树主要蛀干害虫成虫的同时，连续使用还会显著降低林间蛀干类害虫的虫口密度［9］，并且可以连续监测这些蛀干害虫的发生时间、发生量和发生规律，为监测、预报、控制松树主要蛀干害虫提供直接、客观的依据，节省人力、物力。笔者利用连续的林间松墨天牛、短角幽天牛、立毛角胫象和松瘤象蛀干害虫诱捕资料，用似乎不相关线性回归(SUR)方法分析林间各害虫种群的变化及其相互关系，为及时、全面、客观地了解其林间动态和监测预报提供技术支撑。

1 材料与方法

1.1 马尾松蛀干类主要害虫种群数量动态观测

蛀干类害虫引诱剂(原称M－99)，规格为300 mL/瓶，以及配套的小型折叠式诱捕器由浙江省林业有害生物防治检疫局、中国林业科学研究院亚热带林业研究所研制，宁波中化化学品有限公司生产。试验于2006—2010年每年4月至11月进行。试验地设在浙江省仙居县大北地溪林场马尾松人工纯林内，面积 40.2 hm2，海拔66 m，林龄59 a，平均树高约31 m，平均胸径约22 cm。将诱捕器架在距地面1.5 m、两相邻松树间的铅丝上，共设诱捕器22只。每3—4周更换1次引诱剂，每周收虫1次。在室内进行分类鉴定，列出种类名称及数量，共得观测数据131个。

1.2 似乎不相关线性回归分析

似乎不相关回归也称半相依回归、似不相关回归，简记为SUR［10］。SUR是一种特殊的联立方程模型，模型里只有方程间的误差相关而没有联立性，同时各方程影响因变量的自变量数量可以不同，由Zellner［11－12］于 1962 年首先提出。

设{N0、N1、N2、…、Nq}为某林间种群监测序列，描述单个监测序列动态最简单的模型为离散差分方程，其3阶滞后的一般形式为:

式中:Nt为t时诱集到的某种群密度;t是监测次数(t=0、1、2、…、q);f是描述某次诱集到的某种群密度影响下次诱集密度的函数;Et是均值为0的随机误差。

令 Xt=logNt－1，Yt=logNt－2，Zt=logNt－3，rt=log(Nt/Nt－1)，则(1)式化为线性模型为:

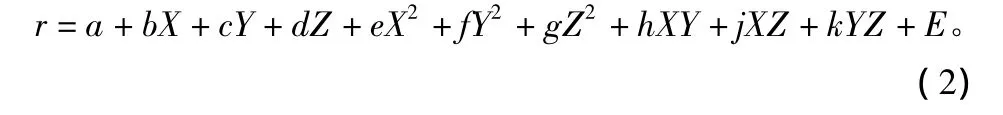
式中:a、b、c、d、e、f、g、h、j、k 是待定系数。

对于n个林间种群的监测序列{Ni0、Ni1、Ni2、…、Niq，i=1、2、…、n}，则有:

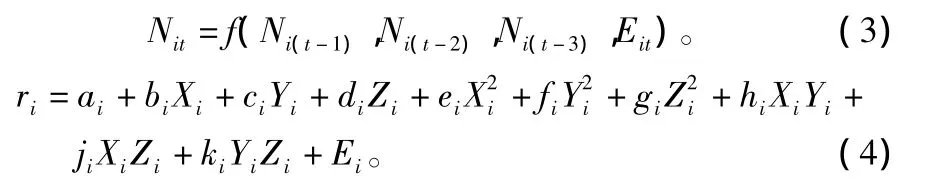
式中:i=1、2、…、n。

将(4)式化为一般形式，则变为n个似乎不相关方程:

式中:yi为(q×1)向量，对应于yi的q个观测值;xi为(q×ki)设计矩阵;βi为(ki×1)未知参数向量;(ei=e1i，e2i，…，eqi)为(q ×1)随机误差向量。

将(5)式写成矩阵形式:

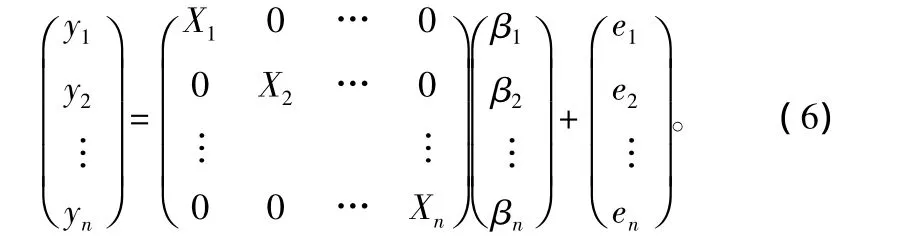
亦即:

假定因变量y的q个观测间相互独立，各方程的误差项 ei间不独立，则有:E(ei)=0，E(ei，ei)=σiiIq，E(ei，ej)= σijIq，i、j=1、2、…、n。

也就是E(e)=0。

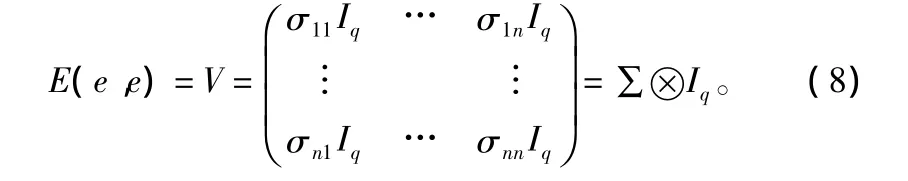
式中:V为模型误差项的方差——协方差矩阵;∑是同一观测点误差项的方差——协方差矩阵;⊗是叉乘(克罗内克乘积)符号。从形式上看，模型的n个方程为各自独立的自变量所解释，各因变量间似乎是不相关的。不过n个方程的同一观测的模型误差项ei的各分量相关，也就是∑为非对角阵，说明这n个方程实际上是通过同一观测的模型误差项ei的各分量相互联系的。

似乎不相关回归模型参数估计的方法及步骤详见文献［15］，［16］106－111。文中的计算及图形绘制均在MATLAB上完成。

2 结果与分析

2.1 模型自变量的确定

对2006—2010年松墨天牛、短角幽天牛、立毛角胫象和松瘤象4种蛀干害虫诱捕数序列的年际间连接做近似处理，也就是连接各蛀干害虫的羽化期，将非羽化期的空间轨线概化为一点［17］。使用偏自相关函数法可以解决模型的滞后代数难以确定的问题［18］，由 Bartlett的 2 /法则确定短角幽天牛、松墨天牛、松瘤象和立毛角胫象4种马尾松主要蛀干害虫林间监测序列模型自变量的最大滞后代数为3代。根据响应面建模原理，对于生态时间序列在确定自变量滞后代数后，通常取(2)式那样的滞后2次型［14］，这样以4种蛀干害虫中任一种群为因变量、该种群自身及其余3种害虫种群作自变量，4种蛀干害虫任一种群模型有自变量36个，为防止自变量间的作用重叠，采用逐步回归法选取自变量，短角幽天牛最终入选的自变量为自身滞后3步序列的观测值(x13)、松墨天牛滞后1步序列观测值的平方(x24);松墨天牛为自身滞后1步序列(x21)、自身滞后3步序列(x23)、自身滞后1步序列的平方(x24)、立毛角胫象滞后1步序列的平方(x44);松瘤象为自身滞后1步序列(x31)、自身滞后2步序列的平方(x35);立毛角胫象为短角幽天牛滞后3步序列的观测值(x13)、自身滞后1步序列(x41)、自身滞后1步序列的平方(x44)。为使自变量序列的长度与因变量序列长度相等，将某种群全部自变量的平均值作为该种群自变量序列的第1个变量值、第2个变量值或第3个变量值。

2.2 似乎不相关线性回归模型的建立

表1列出了分别用最小二乘法对短角幽天牛、松墨天牛、松瘤象和立毛角胫象4种林间种群模型进行独立估计时4个模型间残差的相关系数矩阵。根据表1数据可知，其中3个分模型的残差在置信水平为0.01下相关性显著，表明短角幽天牛、松墨天牛、松瘤象和立毛角胫象4种害虫林间种群存在着一定的相关性，即:cov(ei，ei)≠0，因而对这4个方程的参数进行似乎不相关联立估计能够提高参数估计的有效性和一致性。

分别将使用似乎不相关线性回归方法和最小二乘法拟合的参数结果列于表2。由表2的结果看出，短角幽天牛林间种群数量的某次观测值随自身前3次的观测值(x13)或松墨天牛前1次观测值的平方(x24)的增加而降低。松墨天牛林间种群数量与自身前1次的观测值(x21)成反比，与自身前3次的观测值(x23)、自身前1次观测值的平方(x24)或立毛角胫象前1次观测值的平方(x44)成正比。松瘤象林间种群数量则随自身前1次观测值(x31)的增加而减少、随自身前2次观测值的平方(x35)的增加而增加;立毛角胫象林间种群数量与短角幽天牛前3次的观测值(x13)、自身前1次的观测值(x41)成反比，与自身前1次观测值的平方(x44)成正比。最小二乘法的回归结果与似乎不相关的一致，差别仅体现在回归系数的不同。

2.3 似乎不相关线性回归模型的检验

2.3.1 是否为对角阵的检验

为进一步确认表1的模型残差间相关系数所揭示的可以用似乎不相关方法对4种蛀干害虫林间种群模型进行联立估计，用模型间的方差—协方差矩阵∑是否为对角阵来判断。若∑为对角阵，模型中参数的最小二乘估计量与广义最小二乘估计量相等，而最小二乘估计量就是模型的最优无偏估计，∑是否为对角阵的具体判定方法见文献［16］110，［19］。经计算，拉格朗日乘子统计量λ=76.97＞=9.49，因此拒绝∑为对角阵的假设。

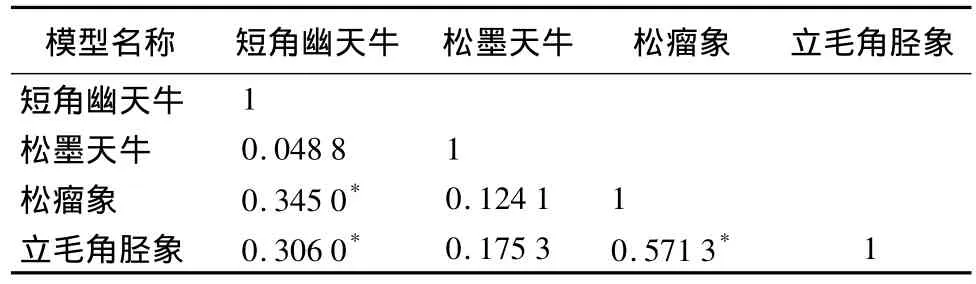
表1 4个分模型间残差的相关系数

2.3.2 模型拟合优度的检验

模型对数据的整体拟合评价用确定系数R2来判定，其计算公式为［19］:

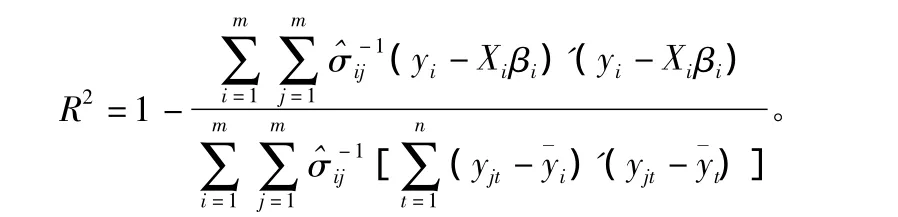
经计算，R2=0.295 2，因此整体模型的相关系数在置信水平为0.01下显著。同时对4种蛀干害虫的分模型进行F检验，结果也表明极显著(表2)。

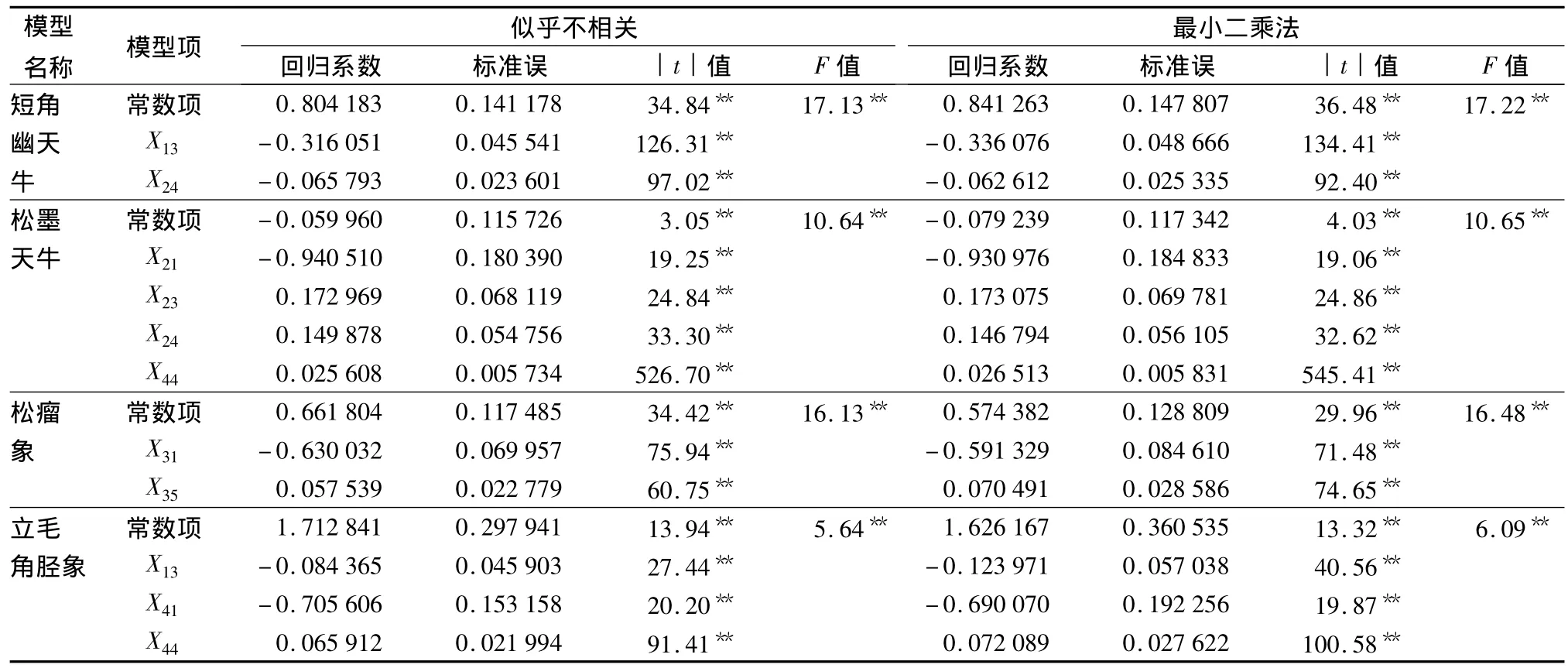
表2 似乎不相关和最小二乘法回归结果

2.3.3 模型回归系数的检验

建立的似乎不相关模型通过了确定系数显著性检验并不代表每个回归方程的自变量Xi都对相应的因变量Yi有显著影响，也许模型中某个方程的自变量Xi对相应的因变量Yi影响不显著，因而需作模型回归系数的显著性t检验［20］40，t检验的结果见表2。从表2可知，用似乎不相关联立估计法得到的各方程回归系数均呈极显著差异，说明各回归方程均拒绝回归系数bi=0的假设，4种蛀干害虫林间种群模型的回归系数均通过t检验。

2.3.4 残差分析

残差的正态性检验:对整体模型的残差进行四元正态分布以及4个分模型的残差进行两两配对的二元正态分布检验［21］表明，各模型的残差均符合四元正态分布或二元正态分布，检验方法及评判标准见文献［22］406－408。

分模型残差的独立性检验:残差的独立性检验通常采用Durbin－Watson方法，其计算公式为:

计算结果为 D短角幽天牛=2.37、D松墨天牛=1.93、D松瘤象=1.92、D立毛角胫象=1.94，各分模型的 D 值约等于2，故各分模型的残差不存在一阶自相关，也不存在多阶自相关，评判标准见文献［20］46－47，［22］364。对各分模型的残差进行自相关计算，其滞后1阶自相关系数和2阶自相关系数均显示相关不显著，这与Durbin－Watson方法的检验结果相符。

2.4 似乎不相关法与最小二乘法估计结果的差异

从表2看出，似乎不相关联立估计的各自变量回归系数与最小二乘参数估计值间均存在偏差，似乎不相关回归联立估计参数的标准误均小于最小二乘估计，因此似乎不相关联立估计的精度高于最小二乘估计。考查4个分模型间因变量的相关系数(表3)，显示各方程间不独立，未将方程间的相关信息纳入考虑范围正是最小二乘法估计精度低的原因，同时似乎不相关模型的残差极差也小于最小二乘法，由此说明用似乎不相关法对4种蛀干害虫种群的监测序列进行建模，所建立的模型在尽可能地反映4种害虫种群监测序列各自的动态变化及相互间影响的同时，也取得了较为满意的拟合精度。

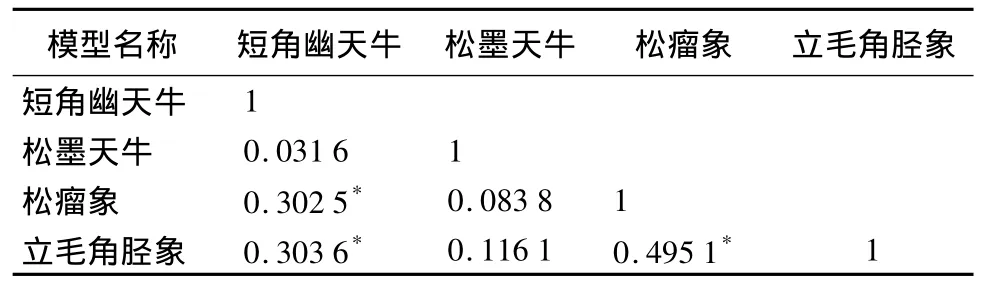
表3 4个分模型因变量间的相关系数

3 结论与讨论

似乎不相关是一种特殊的联立方程模型，它以模型方程间的误差相关性为前提，在模型的拟合过程中根据方程间的误差调整各方程的回归系数，使模型的整体误差趋于最小。通过在林间悬挂诱捕器连续监测马尾松主要蛀干害虫种群动态，由逐步回归法分别筛选出影响各蛀干害虫种群动态变化的因子，然后用似乎不相关法进行联合估计模型的各回归系数，所建立的模型既反映各蛀干害虫种群自身林间的动态变化，又根据模型各方程间的误差调整模型参数，从而间接地反映4种害虫种群间的相互影响与相互联系，并使模型的整体残差达到最小，拟合结果令人较为满意。

由于似乎不相关法联合估计模型回归参数的过程中考虑了方程间的相关信息，故比传统的最小二乘法估计模型参数更合理。不过当各方程的因变量间相关性不大(即∑为对角阵)时，利用似乎不相关法的回归估计结果与最小二乘法的估计结果相同;在样本数量较少的情况下，有时还可能出现最小二乘的估计结果优于似乎不相关线性回归的估计结果，尤其是当方程间的残差相关性较弱时更可能出现上述情况，因此需要在使用似乎不相关线性回归估计前进行Σ是否为对角阵的检验，经检验后再决定采用哪种估计方法［16］124。

似乎不相关法允许模型内各方程的自变量数量不同，因而它比多元多重(也称多对多)线性回归方法具有更大的灵活性;另外，似乎不相关法运用方程间残差的相关信息矩阵来提高参数的估计效率，构成了似乎不相关线性回归法的两个主要特点。在昆虫种群生态中非独立的数据是非常普遍的，忽略观测数据间的相关性会使统计结果偏离真实情况，这为似乎不相关线性回归方法的应用提供了广阔的舞台。

［1］张建军，张润志，陈京元.松材线虫媒介昆虫种类及其扩散能力［J］.浙江林学院学报，2007，24(3):350 －356.

［2］Ikeda T，Oda K，Yamane A，et al.Volatiles from pine logs as the attractant for the Japanese pine sawyer，Monochamus alternatus Hope(Coleoptera:Cerambycidae)［J］.Jap For Soc，1980，62(4):150－152.

［3］Ikeda T，Enda N，Yamane A，et al.Attractants for the Japanese pine sawyer，Monochamus alternatus Hope(Coleoptera:Cerambycidae)［J］.Appl Ent Zool，1980，15(3):358 －361.

［4］Ikeda T，Yamane A，Enda N，et al.Attractiveness of chemicaltreated pine trees for Monochamus alternatus Hope(Coleoptera:Cerambycidae)［J］.J Jap For Soc，1981，63(6):201 －207.

［5］池田俊弥.マツのマダラカシキリの诱引物质とその利用［J］.森林防疫，1986，6(11):95 －99.

［6］王玉嬿，舒超然，孙永春.松褐天牛引诱试验初报［J］.林业科学，1991，27(2):186 －189.

［7］赵锦年，林长春，姜礼元，等.M99－1引诱剂诱捕松墨天牛等松甲虫的研究［J］.林业科学研究，2001，14(5):523 －529.

［8］崔相富，陈绘画，赵锦年，等.括苍山北麓松林间鞘翅目主要昆虫种群动态研究［J］.林业科学研究，2008，21(3):340 －345.

［9］Yoichi K.The pine wood nematode and the Japanese pine sawyer［M］.Tokyo:Thomas Co Ltd，1995:208－209.

［10］张莉莉，史建红.半相依线性回归模型的影响分析［J］.数学杂志，2010，30(1):137 －144.

［11］Zellner A.An efficient method of estimating seemingly unrelated regressions and tests for aggregation bias［J］.J Am Statist Assoc，1962，57:348 －368.

［12］Zellner A.Estimators for seemingly unrelated regression equations:some exact finite sample results［J］.J Am Statist Assoc，1963，58:977 －992.

［13］Turchin P，Taylor A D.Complex dynamics in ecological time series［J］.Ecology，1992，73(1):289 －305.

［14］赵中华，沈佐锐.昆虫种群动态非线性建模理论与应用［J］.生物数学学报，2001，16(4):439 －447.

［15］梁洪川，韩宏，郎素平，等.似乎不相关回归模型及其在老年认知功能研究中的应用［J］.中国卫生统计，2005，22(6):362－364，372.

［16］唐守正，李勇.生物数学模型的统计学基础［M］.北京:科学出版社，2002.

［17］傅军，丁晶，邓育仁.嘉陵江流域形态及流量过程分维研究［J］.成都科技大学学报，1995(1):74 －80.

［18］Berryman A，Turchin P.Identifying the density-dependent structure underlying ecological time series［J］.Oikos，2001，92(2):265－270.

［19］梁洪川.似乎不相关回归模型及其在医学中的应用［D］.太原:山西医科大学，2006.

［20］向东进，李宏伟，刘小雅.实用多元统计分析［M］.武汉:中国地质大学出版社，2005.

［21］Dennis B，Kemp W P，Taper M L.Joint density dependence［J］.Ecology，1998，79(2):426 －441.

［22］苏金明，阮沈勇.MATLAB 6.1实用指南:下册［M］.北京:电子工业出版社，2002.