超声波—真空协同干燥自由水迁移速率1)

杨 飞 何正斌 赵 阳 伊松林

(北京林业大学，北京，100083)

木材真空干燥是一种在干燥环境压力低于常压条件下进行干燥的方法，它可以使木材中的水分在低温下产生沸腾［1］，以干燥速度快(特别是对于较厚的板材)、适用材种多等一系列突出优点，受到了木材干燥界广泛的重视［2］。然而真空状态不仅加快了木材内部水分的移动，同时可能更加快了表面水分的蒸发。因此在干燥过程中，如果含水率较高，且真空度或绝对压力控制不当，木材中的含水率梯度将显著增大，进而导致木材内应力增加，更容易产生干燥缺陷［3］。此外，由于干燥在较低的绝对压力下进行，干燥介质稀少，热量传递困难，从而降低了传热效率［4］。因此，需要研究一种新的处理方法，在保持真空干燥优点的前提下克服缺点。

超声波处理作为一种新兴的技术，由于处理过程中产生的海绵效应、空穴效应等作用，使得超声波对多孔性物质的脱水具有良好的效果［5］。与此同时，由于超声波干燥过程中水分不需要通过汽化就能排除物料，所以超声波可以在低温下对物料进行干燥［6］。近年来，超声波技术越来越多地受到国内外众多学者的关注，但是超声波干燥主要用于食品干燥和干燥过程中含水率的在线检测［7］。结果表明，超声波干燥物料过程中，可以有效地提高材料内部的传热传质过程［8］，而有关用超声波作为处理手段直接干燥木材的报道却不多见。已有的研究表明，超声波处理对自由水的干燥有很好的作用，而对结合水影响不大，而真空干燥更有利于结合水的干燥，所以超声波—真空协同干燥技术不仅能弥补真空干燥的不足，还能结合超声波处理和真空干燥的优点。

本研究采用中国东北林区的核桃楸为试材，在不同的干燥温度、绝对压力、超声波功率及频率条件下，对试材进行干燥，通过对干燥动力性进行对比分析，归纳各因素对超声波—真空协同干燥自由水迁移速率的影响规律，并通过主成分分析和回归方程的确定预测不同条件下的平均自由水迁移速率，了解各因素对协同干燥自由水迁移速率的影响程度，为超声波—真空协同干燥的研究提供一些参考和根据。

1 材料与方法

1.1 材料

试件:核桃楸(Juglans mandshurica)，产于东北林区，无缺陷，直径35 cm，树龄40 a，初含水率50% ～60%。

规格:200 mm(纵向)×100 mm(弦向)×20 mm(径向)，心材，48 块。

处理和保存方法:用环氧树脂封闭试件的两端，冰柜储存。

设备:本试验装置是在真空干燥试验台［9］的基础上改装而成，通过在真空干燥试验台上增加超声波处理设备，即超声波发生器和超声波换能器，形成超声波—真空协同干燥试验装置，如图1所示。

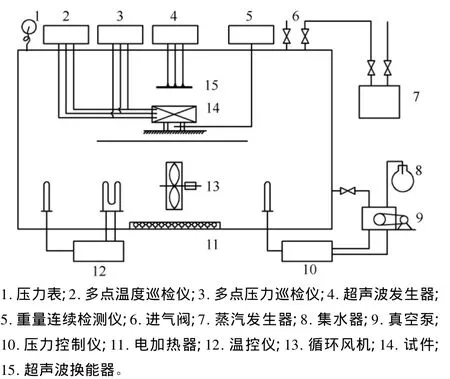
图1 超声波—真空协同干燥试验台

1.2 方法

本试验通过不同条件下自由水迁移速率的对比，分析研究有无超声波处理、干燥温度、绝对压力、超声波功率、超声波频率对超声波—真空协同干燥的影响。具体试验参数与表1所示。

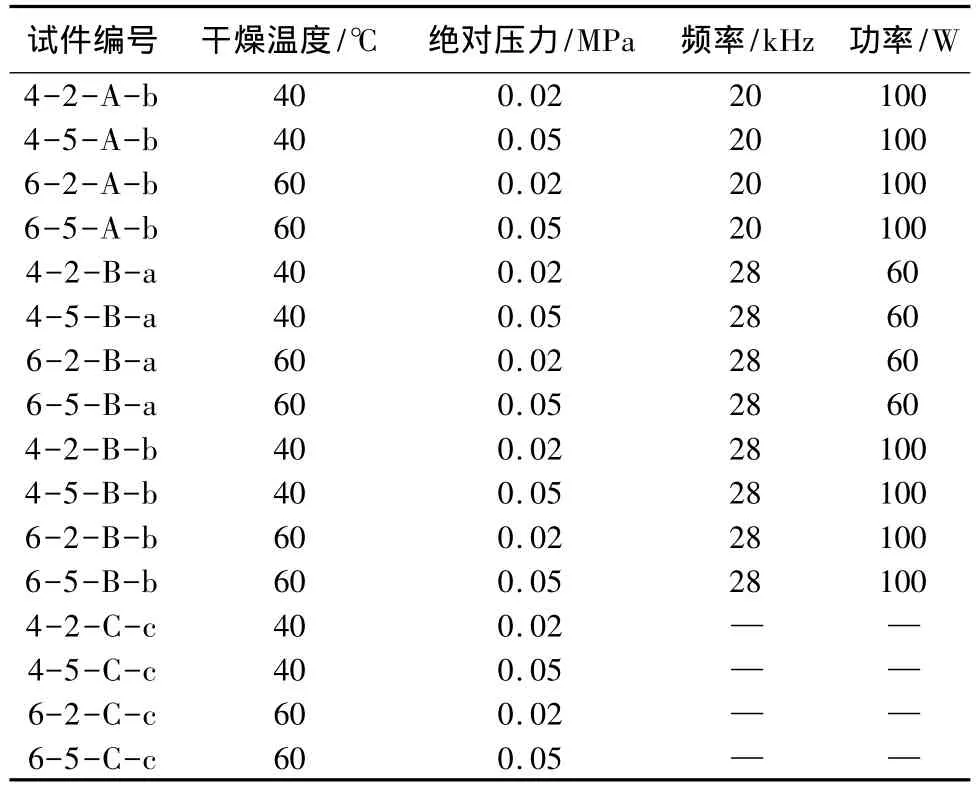
表1 超声波—真空协同干燥试验参数

1.3 步骤

①从试件上截取具有代表性的1 cm厚度的薄片来测量各个试件的初含水率。

②用环氧树脂封闭试件的两端以模拟实际干燥过程。

③对试件按照表1试验参数标号，并记录试件初质量。

④按照表1给出的干燥条件对木材进行干燥，干燥过程中，将试件置入真空干燥箱中，并把超声波换能器放在试件上，按照试件的编号设定参数。试验开始后，每隔2 h进行1次称质量。

⑤待试件的含水率降至纤维饱和点时，停止试验并将试件放入电热恒温鼓风干燥箱，在(103±2)℃下烘至绝干。

⑥重复3次试验取其平均值。通过计算得到干燥过程中各个阶段的含水率，绘制干燥动力学曲线，并对数据进行统计分析，得出各个条件对超声波—真空协同干燥的影响。

2 结果与分析

2.1 干燥动力曲线分析

木材的纤维饱和点是自由水和结合水的分界点，且随着温度的升高而相应降低，温度每升高1℃，纤维饱和点降低0.1%;当温度为20℃时，纤维饱和点为30%［10］。因此可以根据公式(1)算出相应温度下的纤维饱和点。

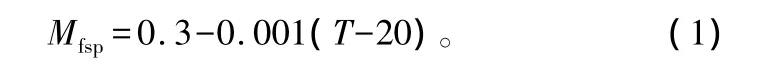
式中:Mfsp为纤维饱和点;T为温度(℃)。

由此可得40℃时纤维饱和点为28%，60℃时纤维饱和点为26%。

2.1.1 不同处理条件下自由水的迁移速率

在不同处理条件下，试材的自由水迁移速率和相应的变化程度如表2所示。

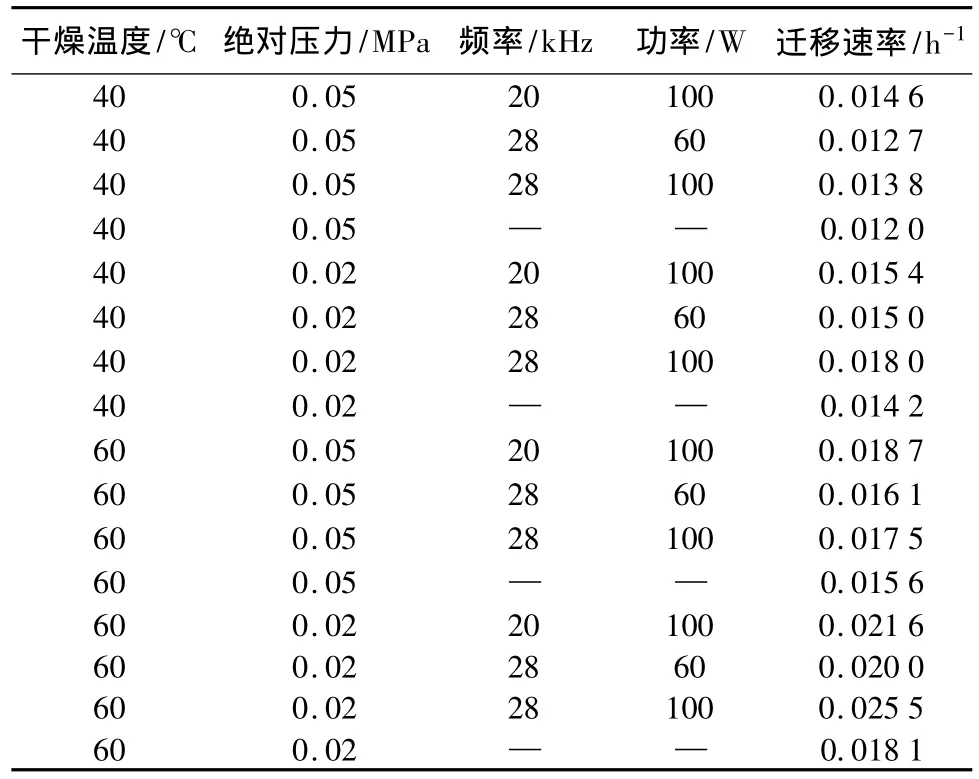
表2 不同处理条件下自由水的迁移速率

2.1.2 不同功率、频率的超声波处理对自由水迁移速率的影响

在不同超声波处理条件下，试材含水率随时间的变化如图2所示。从图2和表2可以看出，在不同条件下，超声波处理可以使试材的自由水迁移速率提高8%～40%，这主要是因为在超声波处理过程中，木材细胞膜和生物质吸收声波能量，使其温度增加，同时由于超声波处理可以产生空穴效应和海绵效应，有效提高了试材内部水分的迁移速度，有利于干燥过程中的传热传质，使得超声波处理可以显著地提高木材的自由水迁移速率。

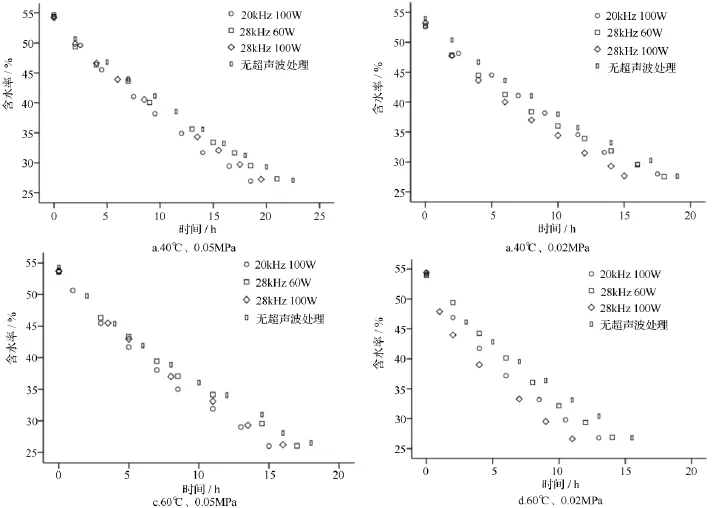
图2 不同温度和压力条件下试材含水率随时间的变化曲线

随着超声波功率的增加，试材的自由水迁移速率越来越快，且在 40 ℃、0.05 MPa，40 ℃、0.02 MPa，60℃、0.05 MPa，60 ℃、0.02 MPa 条件下分别提高了 8.7%、20.0%、9.4%、27.3%。这主要是因为超声波功率越大，试材获得的声波能量越高，而能量越高，试材内部的温度越高，因此可以加快试材的自由水迁移速率。且从图中可以看出，干燥温度越高，超声波功率对协同干燥自由水迁移速率的影响越大。

当绝对压力为0.05 MPa时，超声波频率低，则自由水迁移速率快，且随着温度的升高，自由水迁移速率的提高量分别为5.7%、6.7%;而当绝对压力为0.02 MPa时，超声波频率高，则自由水迁移速率快，且随着温度的升高，自由水迁移速率提高16.7%、18.2%。可以看出，在不同的条件下，超声波频率对自由水迁移速率的影响是不同的，这可能是因为超声波是一种机械波，而试材本身存在着固有频率，当超声波的频率和试材的固有频率一致时会产生共振作用，提高试材的自由水迁移速率。而如果不匹配，则可能降低试材的自由水迁移速率，这种固有频率会受到试材自身和外界环境变化的影响，因此造成了超声波频率对协同干燥影响的不确定性。这种思想与前人在不同频率的超声波对不同厚度板材干燥速率的影响的研究中是一致的。

2.1.3 干燥温度和绝对压力对协同干燥的影响

图3显示了在不同的超声波处理条件下，干燥温度以及绝对压力对超声波—真空协同干燥自由水迁移速率的影响。

从图2和表2中可以看出，在20 kHz、100 W，28 kHz、60 W，28 kHz、100 W 3 种超声波条件下，当绝对压力为0.05 MPa时，随着温度的升高，试材的自由水迁移速率分别提高了26.7%、26.5%、26.7%;而当绝对压力为0.02 MPa时，随着温度的升高，试材的自由水迁移速率分别提高40.3%、33.3%、41.7%。这主要是因为随着温度的升高，木材内部水分子的运动越来越剧烈，有利于水分在木材中的移动，因此自由水迁移速率加快。

除此之外，在相同的条件下，干燥环境的绝对压力越低，试材的自由水迁移速率越快。这主要是因为随着绝对压力的降低，水的沸点也相应地降低，导致水分在木材表面的蒸发速率加快，且由于木材内部的绝对压力不变，所以在干燥过程中试材内外的压力梯度增大，导致水分由木材内部向表面迁移的速度加快，因此加快了干燥速率。

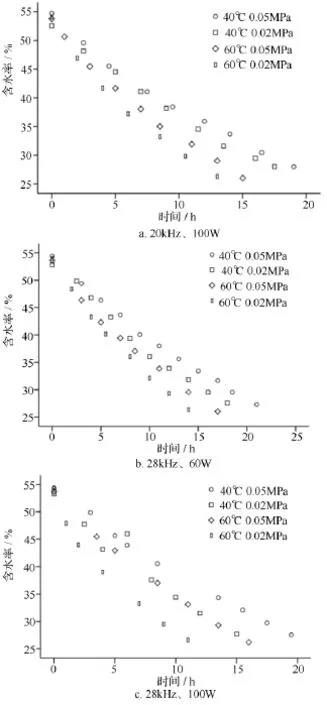
图3 不同频率和功率条件下试材含水率随时间的变化曲线

2.2 主成分分析和回归方程的确定

2.2.1 主成分分析

主成分分析是利用降维的思想，在损失很少信息的前提下把多个指标转化为几个综合指标的统计方法，其中每个主成分都是原始变量的线性组合［11］。这种分析方法可以减少变量的数量，使信息简单易懂，且可以通过各原始变量对主成分的影响程度，分析各原始变量之间的相关性。表3、表4给出了对本试验数据进行主成分分析后的相关参数。

从表3中可以看出，前3个主成分所包含的信息量占总信息的95.419%，因此可以舍去主成分4，对前3个主成分进行分析。从表4可以得到，主成分2反应了100%的温度信息，主成分3主要反应了97.6%的绝对压力信息，因此可以认为主成分2、3分别表示温度和绝对压力的信息。而主成分1主要反应了超声波功率和超声波频率的信息，而超声波功率和频率均为超声波处理参数，因此可以将主成分1视为超声波参数，其具体表达式为:

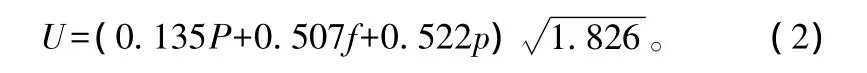
式中:U为超声波参数;P为绝对压力(kPa);f为超声波频率(kHz);p为超声波功率(W)。

因此，通过主成分分析，本试验的参数变量确定为干燥温度、绝对压力以及超声波参数，其中超声波参数通过式(2)得出。

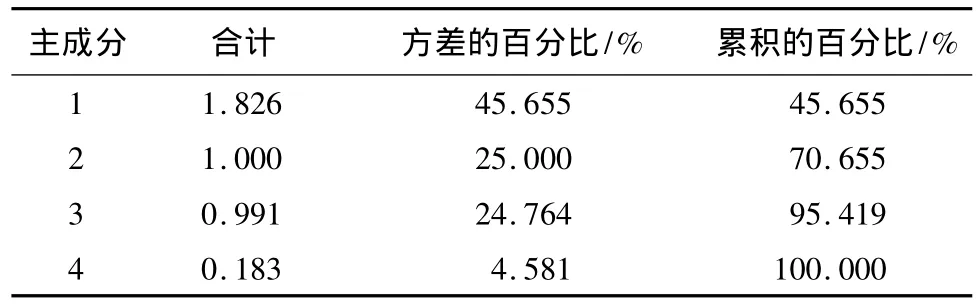
表3 解释的总方差

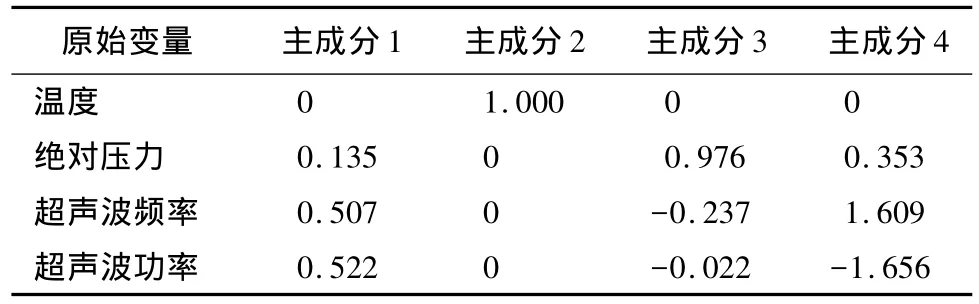
表4 成分得分系数矩阵

2.2.2 回归方程的确定

本试验采用多元统计分析中的逐步回归法对干燥温度、绝对压力以及超声波参数对平均自由水迁移速率的影响进行了回归，并比较了干燥温度、绝对压力、超声波参数对平均自由水迁移速率的贡献率。所得回归方程如下:

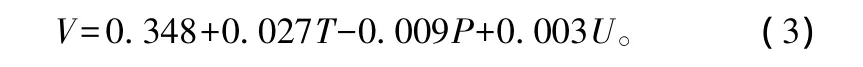
式中:V为平均自由水迁移速率(%);T为干燥温度(℃);P为绝对压力(kPa);U为超声波参数。

回归方程的相关系数R2=0.836，且方程的显著性检验系数均小于0.05，说明所得方程符合要求，且相关性良好。该方程直观反应了干燥温度、绝对压力、超声波参数对平均自由水迁移速率的影响，对不同条件下平均自由水迁移速率的估测具有非常重要的意义。此外，从方程中可以看出，干燥温度对平均自由水迁移速率的贡献率大于绝对压力，且绝对压力大于超声波参数，这对干燥过程中的控制有很好的作用。

3 结论与讨论

超声波的协同可以使真空干燥的自由水迁移速率提高8%～40%，且自由水迁移速率随着超声波功率的增大而加快，但是超声波频率对自由水迁移速率的影响具有不确定性。超声波—真空协同干燥自由水迁移速率随着干燥温度的增高而增快，且绝对压力越小自由水迁移速率越快。

不同条件下的平均自由水迁移速率可通过V=0.348+0.027T－0.009P+0.003U 预测，干燥温度对平均自由水迁移速率的贡献率大于绝对压力，且绝对压力大于超声波参数。

本试验只是对一定条件下超声波—真空协同干燥自由水迁移速率的规律进行了初步的研究，对于其他参数条件下超声波—真空协同干燥特性还有待进一步研究，为超声波—真空协同干燥工艺的制定奠定基础。

［1］张璧光.实用木材干燥技术［M］.北京:化学工业出版社，2005:229.

［2］Mujnmdar A S.干燥过程原理与设备及新进展［M］.史永春，译.济南:济南出版社，2002:114－137.

［3］李帆，陈丽琼，何正斌，等.真空介质条件对木材干燥速率及缺陷程度的影响［J］.干燥技术与设备，2009(6):253－257.

［4］李贤军，张璧光.木材微波—真空干燥基本规律［J］.木材工业，2008，22(3):23－25.

［5］García-Pérez J V ，Cárcel J A，de la Fuente-Blanco S.Ultrasonic drying of foodstuff in a fluidized bed:Parametric study［J］.Ultrasonics，2006，44:539－543.

［6］Voigth H，Krischer O，Schauss H.Special technique for wood drying［J］.Holz als Roh-Werkstoff，1940，11(9):364－375.

［7］Chia-Ju L，Wang S Y，Yang T H.Evaluation of moisture content changes in Taiwan ted cypress during drying using ultrasonic and tap-tone testing［J］.Wood and Fiber Sciense，2011，43(1):57－63.

［8］Jambrak A R，Mason T J，Paniwnyk L，et al.Accelerated drying of button mushrooms，brussels sprouts and cauliflower by applying power ultrasound and its rehydration properties［J］.Journal of Food Engineering，2007，81:88－97.

［9］贾东宇，冯小江，伊松林.杨木真空与常规干燥的对比研究［J］.北京林业大学学报，2009，31(S1):108－111.

［10］Stamm A J，Loughborough W K.Thermodynamics of the Sweeling of Wood［J］.J Phys Chem，1935，39(1):121－132.

［11］何晓群.多元统计分析［M］.北京:中国人民大学出版社，2008:152.