大型公共建筑同向机动车出入口间距计算
2012-06-28钱振东
卓 曦 钱振东 张 宁
(1东南大学智能运输系统研究中心,南京210096)
(2福州大学土木工程学院,福州350108)
具有强集散效应的大型公共建筑出入交通是城市交通的重要组成部分,严重影响城市道路车流通畅性.大型公建机动车出入口交通规划方法决定了建筑出入交通运营模式.大型公建同向出入口间距若不合理,易导致建筑出入交通缺乏足够的缓冲空间,进而引发城市道路交通紊乱、事故频繁.
针对大型公建同向出入口间距设置问题,文献[1-3]指出同向出入口间距影响因素包括运行车速、交通流量和渠化设计等交通条件;文献[4-5]通过实地数据回归分析,提出同向出入口密度和间距参考值;文献[6-7]研究了大型公建交通影响分析方法,提出建筑项目出入口负荷评价和交通组织等经验性意见.可见国内外研究大多以定性分析为主,定量研究深度不足,缺乏基于交通行为机理的出入口选址与间距研究.
根据《城市道路设计规范》[8]中道路两侧大型公建出入口设置规定,本文中城市道路为次干路或支路.针对城市次干路或支路路侧大型公建同向出入口,本文提出一种间距计算方法.通过微观交通行为分析,建立同向出入口最小间距模型,并利用二分法提出若干间距候选方案,采用基于交通仿真的拉开档次法进行方案评价优选.算例结果表明,该方法具有较好的同向出入口间距定量优化能力.
1 同向出入口最小间距模型
1.1 同向出入口影响区域
大型公建同向出入口是指城市道路同侧大型公建(同一个或不同大型公建)开设的同向的机动车出入口.如图1所示,拟定同向出入口影响区域,其中上、下游影响区长度均满足停车视距[9]要求.
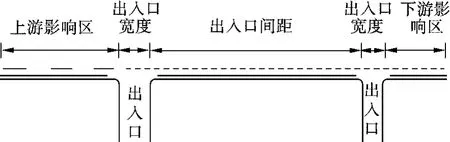
图1 同向出入口影响区域
1.2 最小间距模型
本文假设:①同向出入口影响区域不与相邻交叉口功能区发生重叠;② 城市道路中央采用黄实线或分隔带分离对向交通,即出入口采用右进右出的交通组织形式;③出入口交通管理方式为无控.基于上述假设,提出如下3个最小间距模型.
1.2.1 保证车辆稳定行驶行为的最小间距模型
大型公建同向出入口若间距不足,易导致右转冲突重叠现象(right-turn conflict overlap)[1],即同向出入口右转车流冲突区域相互重叠的现象.该现象导致直行车驾驶员视野内出入口数量过多,即视野内出入口数量多于一个[1].此时驾驶员由于注意力分散而无法维持车辆稳定行驶水平.为保证车辆稳定行驶,针对右转冲突重叠现象,该模型以保证出入口数量合理作为约束条件,即满足相邻同向出入口可视区域分离的临界状态,如图2所示.
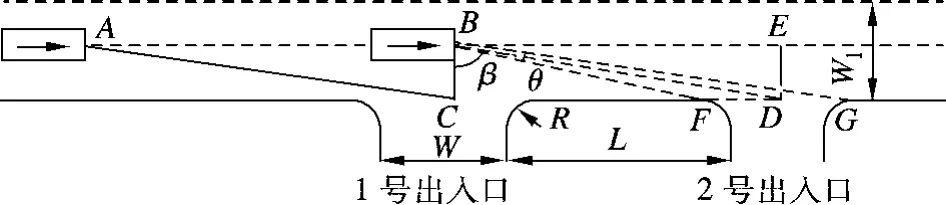
图2 出入口可视区域分离临界状态
图2中,C,D点分别为1,2号出入口的中心点;F,G点为2号出入口的路缘石转角点;A,B,E点为城市道路上出入口的临界可视位置.
该临界状态保证位于B点的车辆恰好看不见2号出入口,则出入口视角满足

式中,θ为出入口视角,(°);θt为出入口视角阈值,(°),即出入口可视的最小视角.
进而利用三角形关系得
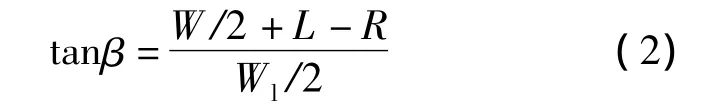
式中,β为BF与BC的夹角,(°);W 为出入口宽度,m;L为出入口间距,m;R为路缘石转角半径,m;Wl为城市道路单条车行道宽度,m.
调查发现θt数值较小,故θ取值很小.因而在允许误差范围内,假设直线BF与BD夹角为θ/2,则有
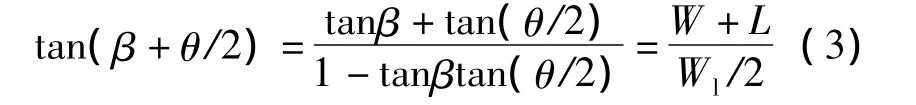
由式(1)~(3)推导出保证车辆稳定行驶行为的最小间距Lste为

1.2.2 减少直行车制动行为的最小间距模型
如图3所示,大型公建出入口存在车辆右转行为.若同向出入口间距不足,跟随右转车的直行车流会因缺乏足够避碰空间而产生较高溢回率,即右转车影响下直行车流发生制动的比例较大[1].

图3 右转车对后随直行车的影响示意图
为减少直行车制动,该模型以保证出入口间城市道路直行车流溢回率合理为约束条件,即

式中,α为直行车流溢回率,%;αmax为直行车流最大溢回率,%.其中

式中,QTB为某时刻出入口间城市路段的制动直行车数量,pcu;QTT为某时刻出入口间城市路段的直行车数量,pcu.假设出入口间城市路段车流密度均衡,则有
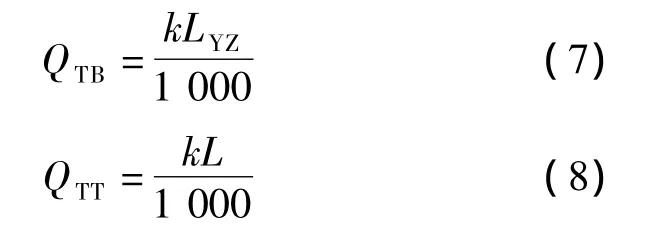
式中,k为路段交通密度,pcu/km;LYZ为右转车对后随直行车流的影响距离,m.根据文献[1],可知
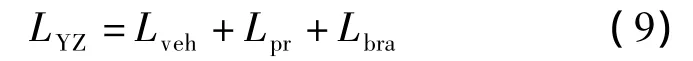
式中,Lveh为直行车车辆长度,m,依据规范[8],小汽车长度取5 m;Lpr为直行车反应距离,m;Lbra为直行车减速制动距离,m.
利用匀速和匀减速运动公式,分别求解Lpr与Lbra,即
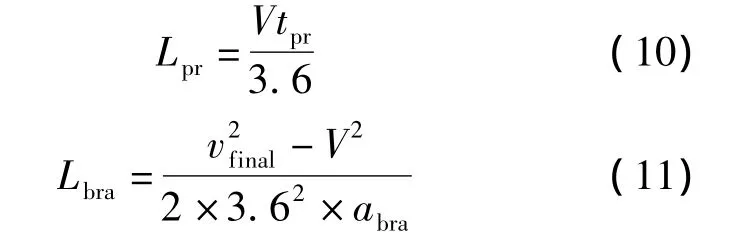
式中,V为城市道路设计车速,km/h;tpr为驾驶员的反应时间,s;vfinal为直行车制动后速度,km/h;abra为直行车制动减速度,m/s2.
由式(5)~(11)得减少直行车制动行为的最小间距Ljzz为

1.2.3 协调相邻出入口车辆合流行为的最小间距模型
如图4所示,1号车选取可插车间隙驶出出入口1.随后于1号车和其下游车辆的车头间距内,2号车驶出出入口2,与1号车进行合流.此时若同向出入口间距不足,2号车所需间隙无法满足,则1,2号车的合流行为无法协调,易导致追尾碰撞.
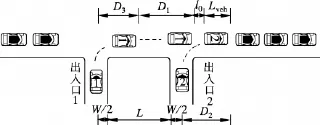
图4 出入口车辆合流示意图
1号车与2号车的合流距离D1定义为2号车驶出出入口2的过程中1号车前进的距离.为协调相邻出入口车辆合流行为,该模型以保证该距离合理为约束条件.该距离允许1号车停车制动,即
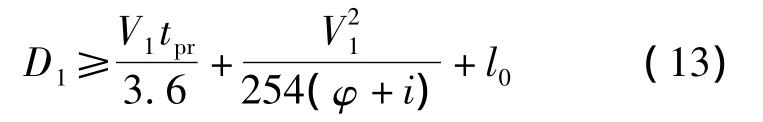
式中,V1为1号车合流入城市道路车流后的车速,km/h;φ为车辆轮胎与路面间纵向摩擦系数;i为城市道路纵坡;l0为两车安全间距,m.
如图4所示,空间距离存在如下关系:
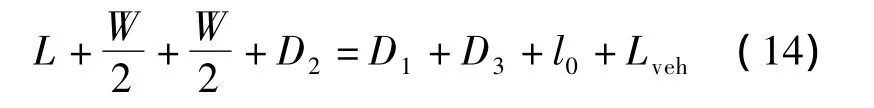
式中,D2为2号车驶入城市道路时前进距离,m;D3为1号车驶入城市道路时前进距离,m.假设驶出出入口的车辆初始速度为0,完成90°转弯后加速,则有
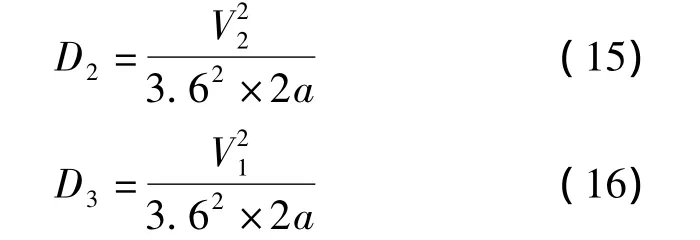
式中,V2为2号车合流入城市道路车流后的车速,km/h;a为车辆汇入城市道路车流的加速度,m/s2.
由式(13)~(16)得协调相邻出入口车辆合流行为的最小间距Lrea为
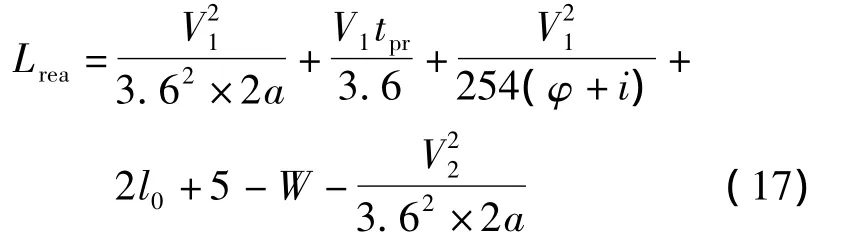
若出入口宽度、车行道宽度、路缘石转角半径等道路线形参数随机取值,则式(4)、(12)、(17)的计算结果均可能成为最小间距极限值.因此本文综合考虑上述3个模型所得最小间距,结合最大间距,通过评价优选求解出入口最优间距.
2 间距方案评价优选
2.1 间距方案生成
基于出入口影响区与交叉口功能区不重叠的假设,计算同向出入口最大间距,其中交叉口功能区长度由停车视距公式求解[9].将式(4)、(12)、(17)的计算结果分别结合最大间距,形成3个间距方案候选区间.参考二分法,以各区间的中值与端点构建新区间,并取各新区间的中值.选取现状间距及各新区间的中值与端点,构建候选间距集合.将该集合的各元素按大小排序,得14个间距候选方案 L1,L2,L3,…,L14.
2.2 基于拉开档次法的间距方案评价
应用基于差异驱动原理的拉开档次法[10]对间距候选方案进行评价.评价步骤如下:
1)将相邻交叉口间微型路网作为仿真评价对象.针对不同出入口间距方案,通过VISSIM的路网评价和车辆信息评价模块[11]分析,获得评价指标数值.其中,高峰时段路网平均速度与平均延误时间分别作为评价指标x1与x2;各类型冲突的平均距碰撞时间作为评价指标x3.各间距候选方案的评价指标值构成评价矩阵X,即

式中,xij为第i个间距方案的第j个评价指标值,1≤i≤14,1≤j≤3.
基于拉开档次法原理,通过评价矩阵一致化将极小型指标变换为极大型指标,即
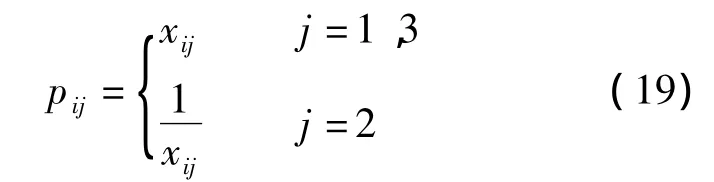
式中,pij为第i个间距方案的第j个评价指标一致化值.
为消除间距方案不同评价指标间的不可公度性,规范化处理后得矩阵Xg,即
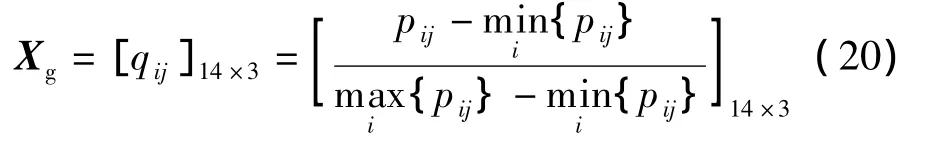
式中,qij为规范化评价指标值.
2)对X进行运算得实对称矩阵H,即

运用Matlab软件计算矩阵H的最大特征值λmax和相应标准特征向量Y.
3)对Y中的元素进行处理,即
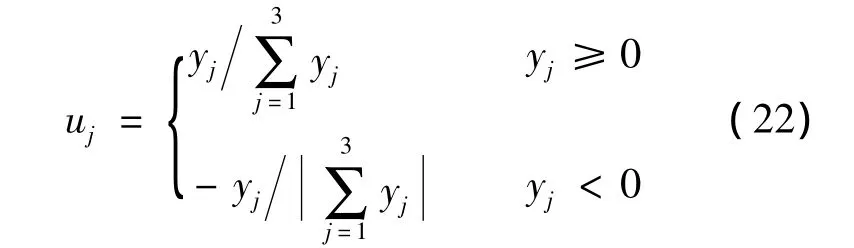
式中,uj为第j个评价指标的权重系数;yj为Y的第j个元素.
4)各评价指标的权重系数构成权系数向量U={u1,u2,u3}T.进而求解第 i个间距方案的组合评价值 zi,即
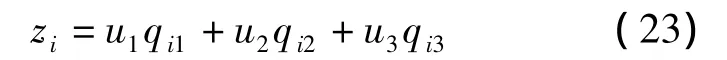
各间距方案按组合评价值大小进行排序.组合评价值越大表明该方案越优.
3 算例及结果分析
以某市次干路单侧的大型公建为算例.相邻交叉口物理间距为362.51 m,同向出入口现状间距为25.58 m.交通组织措施为:该次干路完全隔离对向交通;出入口为无控,且采用右进右出的交通组织方式.该微观区域路网布局及仿真见图5.

图5 路网布局及仿真
3.1 间距方案计算
调查得 W=7.5 m,R=40 m,Wl=3.75 m,θt=0.897 8°,tpr=1.5 s,vfinal=20 km/h,abra=-1.83 m/s2,V1=45 km/h,a=2.5 m/s2,φ =0.6,i=0,l0=3 m,V2=40 km/h.依据规范[8]与文献[1]得,V=40 km/h,αmax=30%.将上述变量及参数值代入式(4)、(12)、(17),算出各最小间距.其中,Lste=118.99 m,Ljzz=156.55 m,Lrea=42.10 m.根据停车视距公式[9]计算可得,出入口上、下游影响区与交叉口上、下游功能区长度均为30.17 m.
基于最小间距与最大间距数值,构建间距方案候选区间.再由二分法计算得14个间距候选方案.其中,L1=25.58 m,L2=42.10 m,L3=88.28 m,L4=118.99 m,L5=134.47 m,L6=145.96 m,L7=156.55 m,L8=172.92 m,L9=174.13 m,L10=180.66 m,L11=191.70 m,L12=199.89 m,L13=209.27 m,L14=226.85 m.
3.2 间距方案评价
在晚高峰时段17:30—18:30调查该次干路交通状况.大型公建临近城市车道交通量为568 pcu/h;同侧2个大型公建交通生成率分别为159与273 pcu/h.VISSIM中,输入仿真区域路网和交通量后,对上述14个间距方案分别进行仿真评价,以获取路网平均速度、路网平均延误时间和平均距碰撞时间等评价指标数值.
用式(18)~(23)进行间距方案评价计算.构建评价矩阵X后,经一致化与规范化,计算得到实对称矩阵H的最大特征值λmax=15.775 4,相应标准特征向量 Y={0.6356,0.6925,0.3412}T.然后计算权系数向量 U={0.380 8,0.414 8,0.204 4}T.最后得出各方案组合评价值zi(1≤i≤14)分别为0.011 0,0.274 4,0.497 5,0.551 9,0.621 5,0.704 1,0.801 6,0.874 3,0.838 7,0.798 0,0.724 8,0.624 5,0.594 6,0.368 3.
分析各间距方案组合评价值可见:相比现状间距,计算所得间距方案具有较大的组合评价值;最大组合评价值为0.874 3,对应间距方案 L8=172.92 m;间距值小于最优间距时,组合评价值随着间距数值减小而减小;间距值大于最优间距时,组合评价值随着间距数值增大而减小.
由于现状间距过小,驾驶员注意水平较低,出入口间城市路段直行车受右转车影响较大,相邻出入口车辆相互干扰严重等交通现象频发,故对应组合评价值最小.若按最优间距进行设计,城市道路综合服务水平最优,能够达到最高的道路通行能力与安全水平.间距值小于最优间距时,随着间距数值逐渐减小,由于驾驶员注意水平、直行车流通畅能力和车辆避追尾能力逐渐降低,道路危险度上升,通行能力下降.间距值大于最优间距时,随着间距数值逐渐增大,由于出入口影响区逐步靠近交叉口功能区,交叉口功能区出现边缘效应,导致功能区边界车流紊乱,道路通行能力与安全水平下降.
4 结语
本文分别针对车辆稳定行驶、直行车制动和相邻出入口车辆合流等行为,研究大型公建同向出入口最小间距模型.以最小间距与最大间距为分析区间,利用二分法求解间距候选方案.针对VISSIM输出的路网平均速度、路网平均延误时间和平均距碰撞时间等评价指标,利用基于交通仿真的拉开档次法计算各间距方案的组合评价值,以选出最优间距.算例结果分析表明利用本文计算方法可获得优于现状间距的多种间距候选方案,进而获得最优间距数值.本文所得最小间距模型假设严格且约束条件单一,故下一步研究将结合邻近交叉口影响,提出多角度、综合性的同向出入口最小间距模型.
References)
[1]Committee on Access Management.Access management manual[R].Washington DC:Transportation Research Board,2003.
[2]Gattis J L,Gluck J S,Barlow J M,et al.Guide for the geometric design of driveways,NCHRP Report 659[R].Washington DC:Transportation Research Board,2010.
[3]Brown H C,Tarko A P.Effects of access control on safety on urban arterial streets[J].Transportation Research Record,1999,1665:68-74.
[4]Levinson H S,Gluck J S.Safety benefits of access spacing[C]//Sixth TRB Conference on the Application of Transportation Planning Methods.Dearborn,MI,USA,1997:307-312.
[5]Dixon K K,Layton R D.The influence of human factors on access management design[C]//4th International Symposium on Highway Geometric Design.Valencia,Spain,2010:1-25.
[6]陈峻,王炜.城市路外停车场出入口交通组织分析[J].东南大学学报:自然科学版,2004,34(1):100-103.Chen Jun,Wang Wei.Traffic organization analysis on entrance and exit of off-road parking lot[J].Journal of Southeast University:Natural Science Edition,2004,34(1):100-103.(in Chinese)
[7]耿化民,蒋阳升,钟永艳.城市规划中微型中央商务区的交通影响分析——以成都市珠江新城为例[J].西南交通大学学报,2009,44(4):609-614.Geng Huamin,Jiang Yangsheng,Zhong Yongyan.Traffic impact analysis of MCBD in urban planning:case research on Pearl River New Town in Chengdu[J].Journal of Southwest Jiaotong University,2009,44(4):609-614.(in Chinese)
[8]北京市市政设计研究院.CJJ 37—1990城市道路设计规范[S].北京:建设部标准定额研究所,1991.
[9]卓曦,张宁,钱振东.大型公建对向机动车出入口间距计算及优选[J].交通运输工程学报,2010,10(4):71-78.Zhuo Xi,Zhang Ning,Qian Zhendong.Spacing calculation and selection on opposite vehicle access of large public building[J].Journal of Traffic and Transportation Engineering,2010,10(4):71-78.(in Chinese)
[10]郭亚军,易平涛.一种基于整体差异的客观组合评价法[J].中国管理科学,2006,14(3):60-64.Guo Yajun,Yi Pingtao.Whole diversity-based reasoning for objective combined evaluation[J].Chinese Journal of Management Science,2006,14(3):60-64.(in Chinese)
[11]Zhuo Xi,Qian Zhendong,Zhang Ning.Research on crossroad access design technology in the functional area of urban interchanges in China[C]//Proceedings of the Tenth International Conference of Chinese Transportation Professionals. Beijing, China, 2010:765-776.
