关于坡印廷矢量教学的几点思考
2012-06-27杜晓燕杨明珊
杜晓燕,杨明珊,安 娜
(1信息工程大学河南郑州450002;2郑州大学,河南郑州450001)
在“电磁场理论基础”课程中,经常要讨论电磁能量流动的问题,此时必然要应用坡印廷矢量(也称为能流密度矢量或功率流密度矢量)。这一内容是电磁场理论教学中的重要内容,不仅其结论要求学生熟练掌握,与其相关的坡印廷定理也要求学生深刻理解,而且这也是更深入地学习电磁波传播和辐射等问题的基础。
这一知识点的教学思路通常是:先由麦克斯韦方程组的两个旋度方程推导得到坡印廷定理的微分形式,再结合定理积分形式推导和能量守恒定理引出瞬时坡印廷矢量,然后将定理推广至频域,并讨论复坡印廷矢量和平均坡印廷矢量[1-5]。
但教学过程中,一般都着重强调能量守恒定理在坡印廷定理中的体现、用坡印廷矢量描述电磁能量流动等内容,甚少讨论坡印廷定理微积分形式的作用、坡印廷矢量与媒质的关系及三个坡印廷矢量之间的关系等。这常常导致学生产生错误的认识:如认为坡印廷定理微分形式与积分形式在引出坡印廷矢量时的作用相同、复坡印廷矢量仅与电磁波的电场和磁场相关等。
1 坡印廷矢量的引出
我们如将麦克斯韦方程组中的全电流定律和法拉第定律的微分形式代入如下的矢量恒等式:
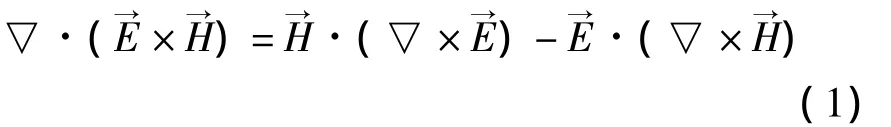
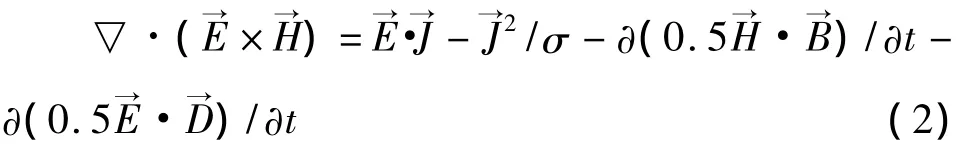
从场的角度可以将上式解读为:空间中任意一点上电源的输出功率、该点上电阻的损耗功率或该点的电/磁功率随时间的变化率,都可以导致E×H空间分布的变化。E×H具有功率的性质。
我们知道电磁场分析过程中,微分形式描述了空间中任意一点的微观情况,而积分形式则给出了一定区域内的宏观关系。所以,微分形式应该是比积分形式更一般的形式。
但是,只有微分形式不可能引出电磁能量流动的实质(即无法研究能量从一点向另一点传输),还必须从坡印廷定理的积分形式出发进行分析。将上式两边分别对任意体积进行积分,可得坡印廷定理的积分形式:
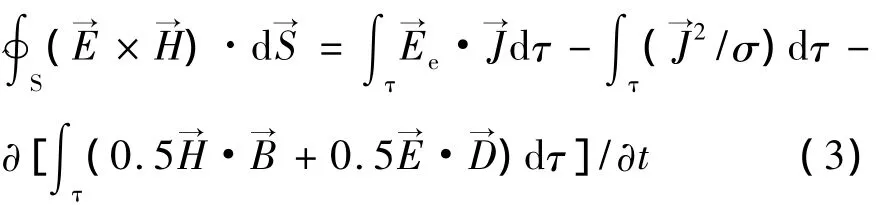
所以,尽管微分形式的坡印廷定理是基本形式,但引入电磁能量的流动特性时,必须强调其积分形式。这一点类似于边界条件讨论过程中,场不连续处采用基本方程的积分形式,而此处则是针对不同点之间的讨论采用定理的积分形式。
2 复坡印廷定理
将复振幅形式的全电流定律和法拉第定律的微分形式代入矢量恒等式:
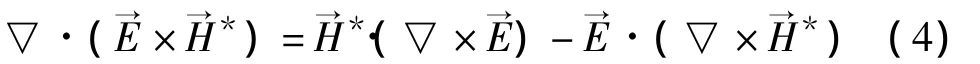
为分析简便,此处仅讨论无源区,可得到复坡印廷定理的微分形式为
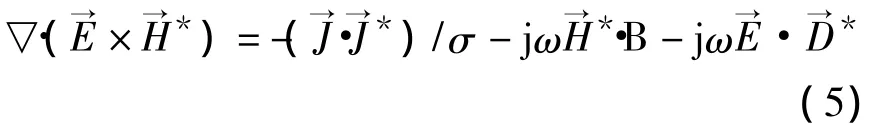
将上式两边分别对任意体积τ积分,得到坡印廷定理的积分形式,可分开写出其实部等式和虚部等式:
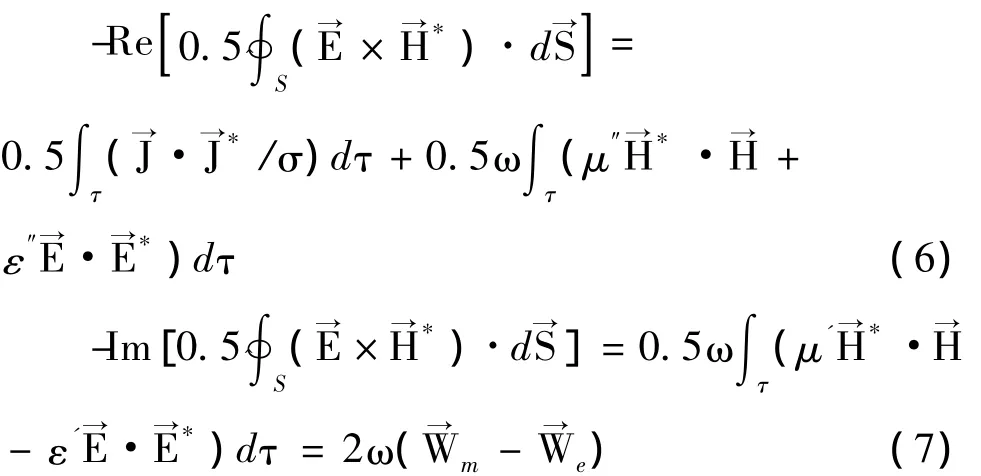
式中,ω= ε'- jε″,μ= μ'- jμ″,Wm为磁场时间平均能量,We为电场时间平均能量。
以上两式均具有明显的物理含义。式(6)表示流出无源闭合区域的电磁能流的周期平均值与这一区域内由于欧姆损耗和介质损耗所消耗的电磁功率的周期平均值相等。式(7)表示当τ内储存的电能和磁能的时间平均值不相等时,呈现为电性或磁性的这部分平均净储能需要用复坡印廷矢量的虚部来平衡。结合电路中的电源、RLC组成的电路,还可以让学生浅显地理解坡印廷矢量。
3 复坡印廷矢量
实际工程中常用到的是瞬时坡印廷矢量和平均坡印廷矢量。有些文献中指出:复坡印廷矢量仅仅是为了计算平均坡印廷矢量方便引入的,无实际物理意义[7]。
但从上述复坡印廷定理的分析不难得出,复坡印廷矢量具有明确的物理含义。其实部给出的是时间平均的有功能流密度,而其虚部则给出振荡的无功能流密度。
由于电磁波传播的本质是波与媒质的相互作用,考虑到媒质特性,不难得出,无功能流密度实质上是由体积τ内的媒质决定的。或者说媒质的特性决定了是否有电磁能量的振荡。
如果体积τ内的媒质为理想介质,其中的电场能量密度和磁场能量密度是完全相等的(电场和磁场相位相同),此时式(7)为零,电磁能量处于平衡状态,复坡印廷矢量无虚部。
如果体积τ内媒质为有损耗媒质,电场的平均能量密度要小于磁场平均能量密度(磁场相位滞后于电场相位),而且媒质损耗越大,滞后的越多。此时电磁能量的平衡需要外界的帮助,复坡印廷矢量存在虚部。
上述结论与体积τ外部的媒质特性无关。
4 三个坡印廷矢量间的关系
在电磁理论中,涉及到的坡印廷矢量有三个:瞬时坡印廷矢量,平均坡印廷矢量和复坡印廷矢量。
由定义可知,瞬时坡印廷矢量为
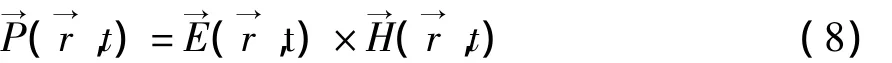
复坡印廷矢量为
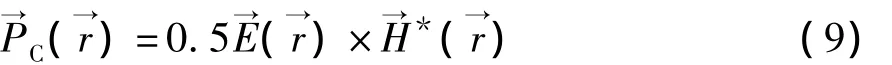
平均坡印廷矢量为
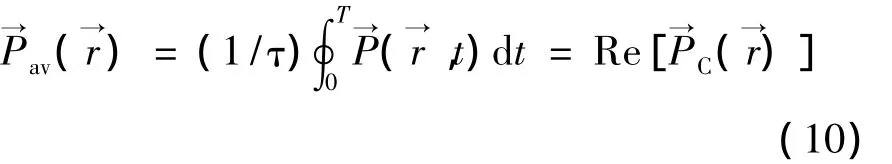
由瞬时坡印廷矢量和复坡印廷矢量均可以计算得到平均坡印廷矢量。
对于正弦电磁波,复振幅的应用可以大为降低计算难度。复坡印廷矢量的求解可以避免复杂的积分运算和降低计算过程中变量的维数等,使平均坡印廷矢量的计算难度有效降低。所以,在讲授过程中应强调复坡印廷矢量在简化数学计算中的意义。
应当强调:瞬时坡印廷矢量和复坡印廷矢量之间无任何直接关系,它们之间并不是瞬时值与复振幅的简单转换关系。这是因为有
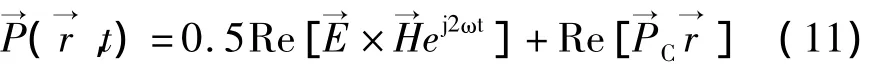
[1] 毕德显.电磁场理论基础[M].北京:电子工业出版社.1985
[2] Bhag Singh Guru,Huseyin R.Hiziroglu著,周克定等译.电磁场与电磁波[M].北京:机械工业出版社.2000.
[3] 龚中鳞.近代电磁理论[M].北京:北京大学出版社.2010.
[4] 陈重等.电磁场理论基础[M].北京:北京理工大学出版社.2008.
[5] 苏东林.电磁场与电磁波[M],北京:高等教育出版社,2009.
[6] 梁昌洪,陈曦.电磁理论中的复参数和复定理[J].南京:电气电子教学学报(自然科学版).2009,(31)5:1-5.
[7] 余恒清,杨显清.电磁场教学指导书[M],北京:北京理工大学出版社,1995.
