双泵并联给水系统切换方式模拟研究

王 鑫，韩伟实，何艺峰，2，幸奠川

（1．哈尔滨工程大学核科学与技术学院，黑龙江哈尔滨150001；2．西北核技术研究所，陕西西安710024）

离心泵是给水系统中的重要设备，在实际应用中为了保证连续供水、提高给水系统稳定性和可靠性，经常设置两台相同的离心泵，一台运行，另一台备用。当一台给水泵停机时另一台能够迅速投入使用，保证系统继续稳定供水［1］。在运行泵发生故障停机、不停止供水检修某一台给水泵以及均衡两台给水泵寿命等条件下，需要进行给水泵切换。

给水泵切换过程中会产生给水流量波动，尤其对于某些需要严格稳定流量输出的系统，这种流量波动将产生较大影响。目前很多学者已对离心泵瞬态理论分析及数值模拟进行了深入研究：田文喜、苏光辉等针对双泵并联系统进行了水锤因素分析［2－3］；吴大转等数值模拟了离心泵在瞬态操作条件下内部流动，与试验结果吻合［4］；杨洪波等分析了核电厂常规电动给水泵切换瞬态特性［5］；张龙飞等研究了转动惯量对船用核动力主泵瞬态特性的影响［6］。

影响切换过程中流量特性的因素较多，主要包括切换时的运行工况、给水泵转动惯量、切换方式等，本文着重研究不同的切换方式对双泵切换过程流量特性的影响。建立双泵并联给水系统模型，通过实验数据对模型进行验证，利用验证后的模型对不同切换方式下流量特性进行研究，为实际工程应用提供参考。

1 试验与模拟

1．1 试验

本试验中设计双泵并联给水系统，为防止支路倒流造成给水泵倒转，在每个支路给水泵下游都安装有一个止回阀。

试验装置结构如图1所示。以常温下水为工质，在接近大气压力条件下进行试验研究。两台给水泵的额定转速1 450r／min。电磁流量计最高流速15m／s，精确度为0．3级（流速≥1m／s），环境温度－10～＋60℃。采用3595系列IMP数据采集器作为动态数据采集系统，对回路流量参数进行检测。

按照图1将试验装置连接并检查，保证一切设备正常工作。试验中在1＃泵运行、2＃泵备用条件下开始，先关闭1＃离心泵，再启动2＃离心泵。

1．2 模型建立

建立模型需要做适当的简化和假设：①给水系统工质为常温常压下水；②流体处于单相状态；③流体沿回路看作一维流动。考虑到离心泵和止回阀的特性和计算精度，通过计算将时间步长定为0．1s。

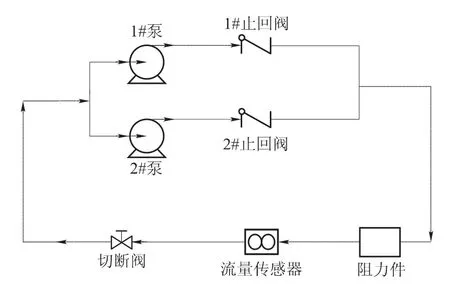
图1 试验装置结构示意图Fig．1 Scheme of experimental device

为进行数值模拟，需要对整个给水系统中的关键设备建立模型。

1．2．1 离心泵模型

离心泵是整个回路中流体流动的动力来源。目前离心泵瞬态过程的相关研究较多［7－9］，在泵开启过程中，流体流动行为主要是由转动部件的惯性及流体惯性控制。离心泵瞬态方程可以写成［10］：

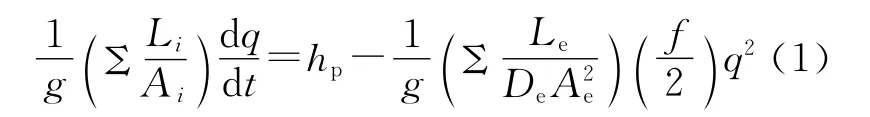
式中：g为重力加速度，m／s2；A为流通截面，m2；De为等效管道直径，m；q为质量流量，kg／s，t为时间，s；hp为泵扬程，m；f为摩擦因子；De为等价管道直径，m；Ae为等价流通截面，m2；下标i表示第i段控制体。

1．2．2 止回阀模型

将这两个数组放在软件数据显示功能模块中的组织数据步骤里，运行效果见图5。结果表明数据显示功能模块能够将接受到的数据正常地显示在布局中。

止回阀稳态与瞬态两种状态进行模拟。1．稳态情况，压降公式为：

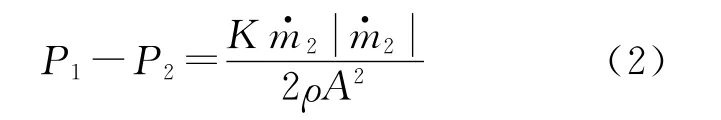
2．瞬态情况，采用以下公式：

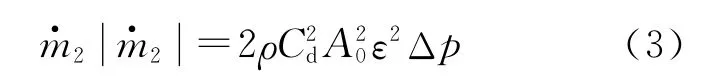
式中：Cd为系数，不同时间下，补偿系数Cd采用不同的计算方法；A0为管道截面积，m2；ΔP为阀门入口和出口之间的压降，Pa。

1．2．3 阻力件模型

阻力件一般采用如下公式计算：

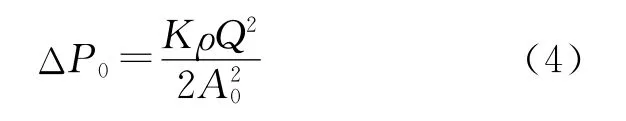
式中：ΔP0为阻力件前后压降，Pa；K为损耗系数；A0为过水断面面积，m2；Q为体积流量，m3／s。

1．3 模型验证与模拟结果

利用建立的双泵并联系统模型，模拟1＃运行泵切换到2＃备用泵的瞬态过程，模拟结果与试验结果比较如图2所示。从图2可以看出试验结果与模拟结果的偏差在误差允许范围内，因此，本模型是合理的。

在双泵切换过程中，系统流量曲线近似呈W形。图2中，在AB段，1＃离心泵由开启状态变为关闭状态，支路流量减少，但是由于离心泵惰转作用，支路仍然会产生正向流量，此时2＃离心泵处于关闭状态，总回路流量下降；在BC段，1＃泵惰转产生正向流量，2＃泵由关闭转为开启，2＃泵支路流量增加，导致整个回路流量增加，到达C点时，1＃泵支路正向流量为零，整个回路流量达到局部峰值；在CD段，1＃泵支路出现倒流，2＃泵支路正流，主回路系统总流量下降；在DE段，1＃止回阀逐渐关闭，倒流减小，2＃泵流量逐步增大，系统总流量增加，到达E点时1＃止回阀全部关闭，系统重新达到稳定状态。

图2 双泵切换流量特性曲线Fig．2 Flow curves in the process of switching pumps

2 切换方式研究

双泵切换方式包括以下三种：

①先启动备用泵后关闭运行泵（方式一）；②先关闭运行泵后启动备用泵（方式二）；③同时开启备用泵和关闭运行泵（方式三）。

实际工程中不同工况下对应不同的泵切换方式：在运行泵发生故障停机，备用泵启用时，双泵切换采用方式一，当时间间隔很小时也可视为方式三；在不停止供水条件下检修某一台给水泵或者均衡两个给水泵寿命等计划内切换时，可根据需要采用三种启动方式的任意一种。

2．1 模拟结果

利用已经验证的系统模型对三种不同泵切换方式下系统流量波动情况进行模拟，结果如图3所示。

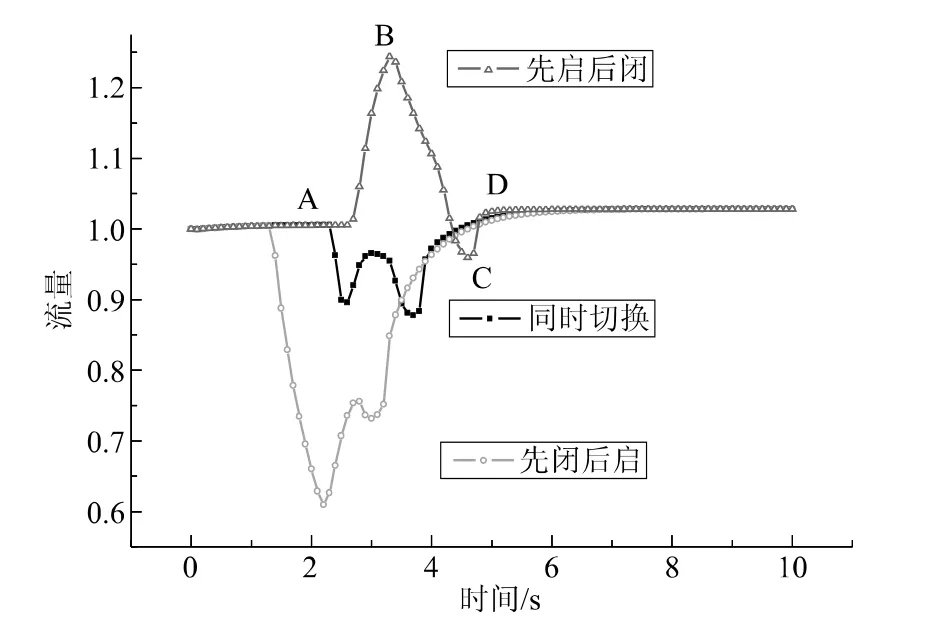
图3 不同泵切换方式下系统流量波动曲线Fig．3 Flow curves in different switching mode

（1）先启后闭，在AB段，备用泵首先启动，此时运行泵（1＃）满功率运行，备用泵（2＃）流量增加，1＃、2＃支路正流，给水系统流量增加，流量超过正常供给值，到达B点时系统流量最大；此后1＃泵关闭，1＃支路流量减少，但是1＃泵在惯性惰转作用下继续正向给水，2＃泵流量继续增加，系统流量减小；之后1＃泵停止，所在支路出现逆流，2＃泵支路正流，直到C点系统流量达到最小；在CD段，1＃止回阀逐渐关闭，倒流减小，系统总流量增加，到达D点时1＃止回阀全部关闭，系统流量达到稳定。由于采用先开启后关闭的切换方式，系统流量在波动阶段前期大于稳定输出流量值，切换过程流量输出总和大于稳定输出时的流量总和。

（2）先闭后启与同时启闭切换方式，双泵切换过程中，系统流量特性曲线近似成W型，其形成原理见前文1．3节中W型曲线形成机理分析。

2．2 不同切换方式比较分析

对于计划内双泵切换，三种切换方式均可采用。方式一中系统失水量小，最低流量较高，系统稳定时间短，但流量波动较大，在切换瞬态过程中系统总流量大于稳定输出时流量。与方式一相比，方式二、三在双泵切换过程中失水量较大，系统总流量低于稳定输出时供水量。

对于非计划内事故工况双泵切换，可采用方式二、三，即运行泵先停，备用泵迅速启动。比较发现方式三在双泵切换过程中系统失水量小，最低流量较高，系统恢复稳定时间短。在实际工况中，采用同时启闭方式，即尽量减少双泵切换时间间隔将更易于缓解流量波动问题。

3 切换时间间隔研究

不同的切换方式具有不同的流量特性曲线，对于切换方式一和方式二，切换过程时间间隔也发挥着明显的作用。通过模拟不同时间间隔下系统流量的波动，比较时间间隔大小对系统流量特性的影响。

3．1 先启后闭方式切换时间间隔研究

先启后闭双泵切换方式在不同时间间隔下系统流量波动如图4所示，切换时间间隔为分别0．5s、1s和1．5s。图4表明，对于不同时间间隔，切换过程中流量曲线形状相近，AB段内2＃备用泵开启，流量曲线相重合；时间间隔大小不同，系统流量峰值出现的时间和位置也不同，即间隔时间越长，峰值出现越晚、位置也越高，总体上系统流量波动也将愈加明显。不同时间间隔直接影响1＃运行泵关闭时刻，时间间隔越长，运行泵关闭延迟越长，具体表现为流量曲线峰值位置延时并且上移，造成后续的流量波动阶段以及流量恢复稳定阶段流量波动更加明显。因此，对于先启后闭切换方式，切换间隔时间越长，系统流量波动也更大，给水稳定性受到更大的影响。

3．2 先闭后启方式切换时间间隔研究

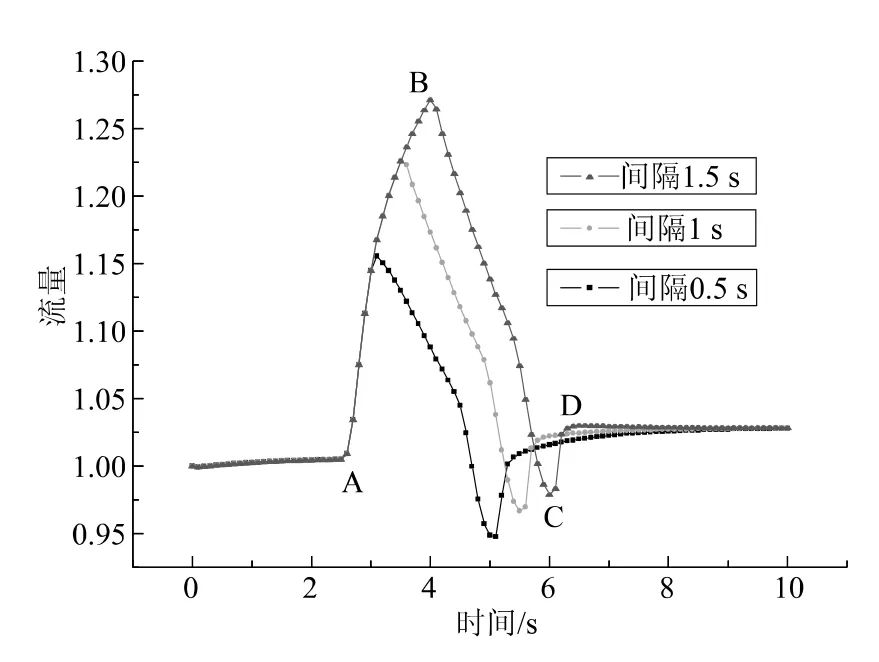
图4 先启后闭方式切换下系统流量波动Fig．4 Flow curves in the switching mode of closing one pump after starting another one

先闭后启双泵切换方式在不同时间间隔下系统流量波动如图5所示，切换时间间隔分别为0．5s、1s和1．5s。由图5可知，对于三种不同时间间隔切换方式，切换过程中流量曲线形状近似，AB段内1＃运行泵关闭，流量曲线相重合；间隔时间长短影响了系统流量波谷出现的时间和位置，间隔时间越长，系统流量波谷出现越晚、出现位置越低，总体上系统流量波动也将愈加明显。不同时间间隔直接影响2＃备用泵开启时刻，时间间隔越长，备用泵开启延迟越长，具体表现为流量曲线波谷位置下移，造成后续的流量波动阶段以及流量恢复稳定阶段流量波动更加明显。因此，对于先闭后启切换方式，切换间隔时间越长，系统失水量越大，流量波动也更大，给水稳定性受到更大的影响。

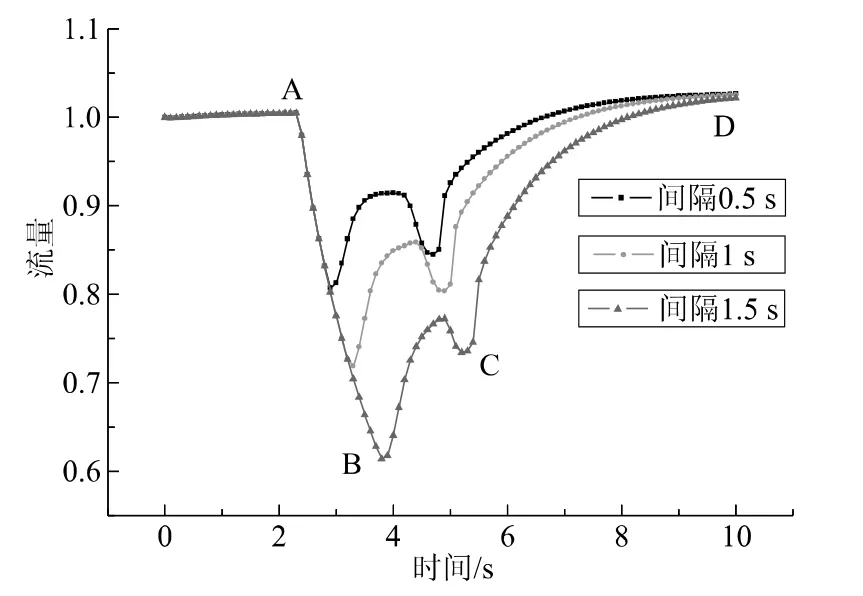
图5 先闭后启泵切换方式下系统流量波动图Fig．5 Flow curves in the switching mode of starting one pump after closing another one

综上，无论采取哪种切换方式，缩短泵切换时间间隔，能减小系统流量波动，使系统在较短时间内恢复稳定工作。

4 结论

对双泵并联给水系统进行了建模，通过试验证明了模型的准确性。模拟不同双泵切换方式条件下系统流量波动过程，得到以下结论：（1）模拟结果与实验结果偏差在允许的范围内；（2）先启后闭切换方式下系统失水量小，最低流量大，同时启闭切换方式系统流量波动最小，系统恢复稳定时间短；（3）采用同时启闭方式在泵切换过程中系统失水量小，最低流量较高，系统恢复稳定时间短；（4）双泵切换时间间隔越短，系统流量波动越小，系统稳定时间越短，在实际工况中，要尽量减小切换时间间隔。

［1］ 郭强，赵新文，蔡琦．反应堆冗余泵组的共因失效分析［J］．核动力工程，2009，30（5）：89－92．

［2］ Wenxi Tian，GH Su，Gaopeng Wang，et al．Numerical simulation and optimization on valve－induced water hammer characteristics for parallel pump feedwater system［J］．Annals of Nuclear Energy，2008，35（12）：2280－2287．

［3］ TIAN Wenxi，SU Guanghui，WANG Gaopeng，et al．Mitigating check valve slamming and subsequentwater hammer events for PPFS using MOC［J］．Nuclear Science and Techniques，2009，20（2）：118－123．

［4］ 吴大转，许斌杰，李志峰，等．离心泵瞬态操作条件下内部流动的数值模拟［J］．工程热物理学报，2009，30（5）：781－783．

［5］ 杨洪波，吴焕云．核电厂常规岛电动给水泵切换瞬态分析［J］．核电技术论坛热力发电二〇二，2011，40（1）：82－83．

［6］ 张龙飞，张大发，王少明．转动惯量对船用核动力主泵瞬态特性的影响研究［J］．船海工程，2005，（2）：55－57．

［7］ Kolev N，Petrov N，Ivanov B，et al．Simulation of the VVER－1000pump start－up experiment of the OECD V1000CT benchmark with CATHARE and TRAC－PF1［J］．Progress in Nuclear Energy，2006（48）：922－936．

［8］ Rohani M，Afshar M H．Simulation of transient flow caused by pump failure：Point－Implicit Method of Characteristics［J］．Annals of Nuclear Energy，2010（37）：1742－1750．

［9］ 郭玉君，张金玲，秋穗正，等．反应堆系统冷却剂泵流量特性计算模型［J］．核科学与工程，2005，15（3）：220－231．

［10］ Kazem Farhadi，Anis Bousbia－salah，Franscesco D’Auria．A model for the analysis of pump start－up transients in Tehran Research Reactor［J］．Progress in Nuclear Energy，2007（49）：499－510．