基于三维MC-SN耦合方法的PWR压力容器快中子注量计算基准分析
2012-06-26韩静茹陈义学石生春袁龙军陆道纲
韩静茹,陈义学,石生春,袁龙军,陆道纲
(1.华北电力大学核科学与工程学院,北京102206;2.环境保护部核与辐射安全中心,北京100082)
屏蔽系统设计是核装置工程设计的核心内容之一,其设计优劣直接影响工程造价及工作人员与周围环境的辐射安全。选取合适的屏蔽计算方法是保证屏蔽系统设计质量的关键。华北电力大学在辐射屏蔽方法及应用方面开展了大量的研究工作[1-5]。蒙特卡罗方法(MC)和离散纵标方法(SN)是最常用的屏蔽计算方法。MC方法的优点是可以精确模拟复杂几何模型,但计算耗时,尤其对于屏蔽计算中常见的深穿透问题,有的甚至根本无法得出计算结果。尽管有MC分段计算[6]方法的研究用于解决深穿透的问题,但由于分段计算中MC统计误差的连续传递性,但这仍旧是其在研究和实际应用中最大的困难。与MC方法相比,SN方法特别适合解决深穿透问题但却难以精确描述复杂几何模型。对于大型复杂核装置屏蔽计算问题,MC方法或SN无法提供可靠的计算结果。
为了解决这类具有复杂物理过程与几何结构,同时具有深穿透特点的屏蔽问题,结合MC和SN方法优势的耦合计算方法成为首选。如基于MC和SN方法开发的耦合程序MCNPANSIN[7]、 HETC96-ANISN[8]、 HERMESANISN[9]、MCNP-DORT[7]、MCNP-TRIDENT[10]等。然而这些程序仅支持MC方法与一维或二维离散纵标法的耦合,不支持三维屏蔽计算,难以满足现代核装置精确屏蔽设计的要求。陈义学等开发了三维 MC-SN耦合方法,并用于直角坐标系下国际聚变材料辐照装置(IFMIF)屏蔽设计计算[11-12]。但该耦合方法在圆柱坐标系中应用时存在限制。本工作对三维MC-SN耦合方法进行改进,然后将其用于圆柱坐标系下PWR压力容器快中子注量计算,并与基准报告结果进行比较分析,验证三维 MC-SN耦合方法计算结果的可靠性,从而保证为屏蔽系统优化设计的质量提供有力的技术支持。
1 MC-SN耦合方法及程序
MC和SN方法是求解中子输运问题的两种不同方法。其中MC方法属于非确定论方法,通过对大量中子行为观察分析,用统计平均的办法,推测出估计量之解。而离散纵标SN方法属于确定论方法,是用数值方法求解玻尔兹曼输运方程的重要方法之一。为了精确处理大型复杂核装置屏蔽问题,结合MC和SN方法的优势,开发了三维MC-SN耦合方法。一般来说,耦合屏蔽计算分析可以遵循下面的步骤:(1)模型分解为适合 Monte Carlo模拟的源区或复杂几何模型及屏蔽区SN模型;(2)定义Monte Carlo模型与SN模型的连接面;(3)对源模型进行Monte Carlo模拟,得到通过连接面的粒子径迹信息;(4)将记录的Monte Carlo粒子径迹转化为SN角通量分布;(5)根据得到的角通量分布生成SN程序所需的面源文件;(6)利用面源进行SN计算,得到厚屏蔽区的粒子通量分布。
为了耦合两种不同的方法,关键是MC模拟的公共面粒子径迹到SN角通量密度的转换,即将MC粒子的位置、能量和飞行方向分别与SN空间网格、能群和离散方向一一对应转换。三维 MC-SN耦合方法采用映射方法[11-12]实现上述转换。已有的三维 MC-SN 耦合方法只考虑了直角坐标系下MC粒子飞行方向与SN离散方向的转换,在圆柱坐标系下却不适用。本工作针对上述问题进行了如下改进。MC描述几何时以直角坐标系为基础,MC粒子径迹包括粒子飞行方向分别与x,y,z坐标轴的夹角余弦值u,v,w,通过三个夹角余弦值可以确定粒子运动方向在直角坐标系中对应的极角θ和方位角φ。而在圆柱坐标系中,SN离散方向区域可由极角θ和ω来表示。其中ω是粒子方向和Z轴形成的平面与R和θ形成的平面间的夹角,可认为是圆柱坐标系中对应的方位角。当点的位置及其空间坐标R改变时,R和θ的坐标轴方向亦随之发生改变。将圆柱坐标系中的方位角ω转换为直角坐标系中的方位角φ,实现SN圆柱坐标系下离散方向与MC径迹中的粒子方向对应转换。同时本工作将原三维MC-SN耦合方法中圆柱坐标系几何范围由(-90°,90°)扩展到(0°,360°)。
三维MC-SN耦合计算程序系统流程图如图1所示。其中Monte Carlo模拟使用国际通用的粒子输运程序MCNP[13],三维离散纵标法计算使用美国橡树岭国家实验室开发的三维离散纵标法程序TORT[14],而接口程序则基于上述介绍的三维映射方法,将MCNP计算得到的粒子径迹转换为TORT计算所需的边界源文件。
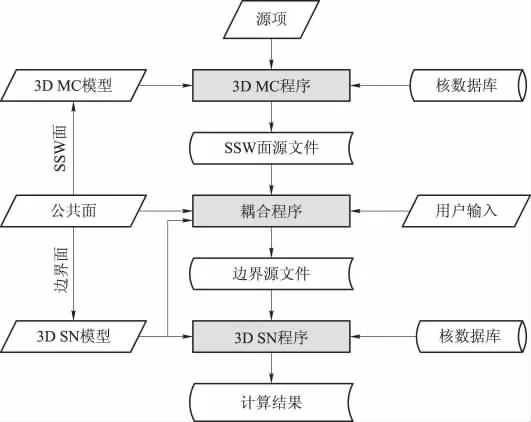
图1 MC-SN三维耦合计算程序系统流程图Fig.1 Flow chart of the program system for three-dimensional coupled MC-SN
2 MC-SN基准测试
三维MC-SN耦合屏蔽计算方法采用BNL(Brookhaven National Laboratory)开 发 的NUREG/CR-6115[15]压水堆基准例题进行验证计算,并与基准报告提供的 MCNP、DORT结果进行比较分析。
2.1 基准模型描述
基准计算对象选取 NUREG/CR-6115(BNLNUREG-52395)中标准的IN-OUT 堆芯装载模式的反应堆。其堆芯由204个燃耗深度不同的组件组成,堆芯外依次由围板、吊篮、热屏蔽、压力容器等结构组成。堆芯高度为335.28cm,堆芯上底面反射层厚度为32.865cm,堆芯下底面反射层厚度为13.97cm。压力容器内半径为219.075cm,厚21.59cm,包括0.635cm内表面不锈钢覆盖层。
选取热屏蔽内表面作为耦合计算的公共交界面,将模型划分为MC模拟区和SN模拟区。堆芯到热屏蔽使用MCNP程序计算,为了减少外围组件不可忽略的径向功率梯度对结果的影响,建立堆芯外围3层组件15×15的pin-bypin精细模型。同时考虑粒子散射对交界面源造成的影响,将MC模型扩建到压力容器内表面。热屏蔽到压力容器部分属于模型相对简单的SN模拟区,采用TORT进行建模计算。接口程序的主要功能是将MCNP计算获得穿过热屏蔽内表面的中子径迹信息(包括权重、空间位置、能量、飞行方向等)转换为TORT边界源文件,用于SN模拟区屏蔽计算,实现三维MCSN耦合计算。
选取与基准报告中相同的计算模型,即1/8反应堆模型。0°和45°处采用反射边界,压力容器外表面设置真空边界,同样在顶部和底部反射层的外表面采用轴向真空边界条件。图2a和2b分别给出了三维耦合计算几何模型的水平和垂直剖面图。压力容器内壁峰值位置为R=219.393cm,Z=125.488cm;压力容器1/4峰值位置为R=224.473cm,Z=125.488cm;压力容器内壁焊缝位置为R=219.393cm,Z=67.104 8cm,具体如图2b所示。

图2 a 1/8压水堆模型水平剖面图Fig.2a Horizontal section of 1/8PWR model
2.2 计算结果及分析
MCNP计算准确地描述计算问题的几何结构及材料,采用ENDF60截面数据库,它是基于ENDF/B-Ⅵ评价核数据库开发的连续能量截面数据库。堆芯内区组件采用组件平均功率,堆芯外围组件15×15的精细模型,并采用pin-by-pin的精细功率分布。堆芯瞬发中子采用混合裂变谱,考虑燃耗对多种裂变同位素的影响。TORT计算采用R-θ-Z几何模型,P3阶勒让德展开和S8全对称高斯求积组。R、θ、Z三个方向分别划分了45、20和38个网格。同时计算采用了基于ENDF/B-Ⅵ评价核数据库的多群截面库MATXS10,包括30群中子和12群光子的截面。
NUREG/CR-6115基准报告中,给出了采用MCNP/4A及DORT计算得到的轴向峰值处和焊缝处压力容器内不同厚度处(内表面、1/4T)的快中子注量率(E>1.0MeV)圆周方向分布结果。本文采用 MC-SN耦合程序计算,由于MATXS10库中子能群在1.0MeV处并无能群边界,因此对0.823~1.35MeV能群段内的中子进行插值处理,得到E>1.0MeV的快中子注量率,并与基准报告提供的结果进行比较。分别如图3~图5所示。
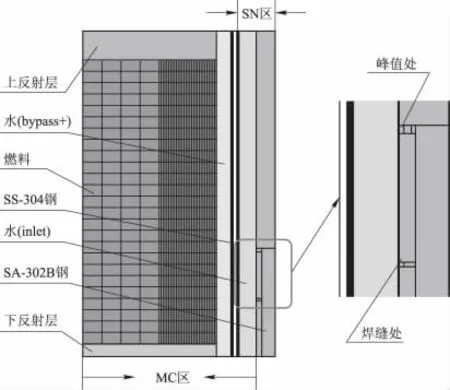
图2 b 1/8压水堆模型垂直剖面图Fig.2b Vertical section of 1/8PWR model

图3 轴向峰值处压力容器内表面快中子注量率(E>1.0MeV)圆周分布曲线Fig.3 Circular distribution of E>1.0MeV flux at pressure vessel inner wall axial peak location
图3给出了轴向峰值处压力容器内表面E>1.0MeV的快中子注量率周向分布。从中可以看出,MC-SN计算得到的快中子注量率结果与NUREG/CR-6115基准报告中的 MCNP和DORT结果趋势基本一致,吻合较好。与MCNP结果相比最大误差小于7.45%,平均误差小于0.25%。

图4 轴向峰值处压力容器1/4壁厚处快中子注量率(E>1.0MeV)圆周分布曲线Fig.4 Circular distribution of E>1.0MeV flux at pressure vessel T/4axial peak location
图4给出了轴向峰值处压力容器1/4壁厚处E>1.0MeV的快中子注量率周向分布。从中可以看出,MC-SN计算得到的压力容器快中子注量率结果与NUREG/CR-6115报告结果趋势一致,与MCNP结果相比最大误差小于11.96%,平均误差为3.68%。

图5 焊缝处压力容器内表面快中子注量率(E>1.0MeV)圆周分布Fig.5 Circular distribution of E>1.0MeV flux at pressure vessel lower weld
图5给出了焊缝处压力容器内表面E>1.0MeV的快中子注量率周向分布。从中可以看出,MC-SN计算得到的压力容器快中子注量率结果与 NUREG/CR-6115PWR报告结果差别较小,与MCNP结果相比最大误差小于7.57%,平均误差为2.64%且趋势一致。
从图3~图5可以看出,MC-SN计算结果与基准报告中MCNP和DORT计算结果相比基本吻合,少数角度对应的误差相对大些,产生的原因主要有:(1)不同的计算程序基于的理论方法不同;(2)程序使用的核截面库不同,MCNP程序使用的是连续截面数据库,而TORT和DORT程序使用的是多群截面数据库,理论精度低于连续截面数据库;(3)几何建模差别。MCNP较DORT程序对几何模型和源项进行更精细的描述,减少了模型简化近似引入的偏差,使其结果更可信。
3 结论
结合MC精确模拟复杂几何和SN适合解决深穿透问题优势的三维MC-SN耦合方法,用于解决大型复杂核装置屏蔽计算问题的难题。为了验证耦合方法及程序系统的可靠性,采用BNL压水堆基准例题对其进行了基准测试。耦合计算取得了与报告提供的与基准报告提供的MCNP和DORT基本一致的结果,验证了方法的有效性和程序使用的正确性。表明三维MC-SN耦合方法可以为屏蔽系统优化设计提供有力的技术支持。
[1]Zhang Bin,Chen Yixue,Wang Weijin,et al.Preliminary Shielding Analysis in Support of the CSNS Target Station Shutter Neutron Beam Stop Design[J].CPC(HEP &NP),2011,35(8):791-795.
[2]靳忠敏,陈义学,石生春,等 .基于MCNP的压力容器快中子注量率计算参数敏感性分析[J].原子能科学技术,2011,45(2):195-199.
[3]李硕,陈义学,杨寿海 .基于二维离散纵标法的压力容器快中子注量计算参数不确定度分析[C].第十三届反应堆数值计算与粒子输运学术会议 .西安,2010.
[4]石生春 .基于蒙特卡罗方法的压水堆压力容器快中子注量率的计算分析[D].北京:华北电力大学,2010.
[5]陈义学,吴宜灿,U.Fischer.国际聚变材料辐照装置屏蔽中子学设计研究[J].原子核物理评论,2006,23(2):170-173.
[6]钟兆鹏,施工,胡永明 .用 MCNP程序计算水平辐照孔道屏蔽 [J].清华大学学报(自然科学版),2011,41(12):16-18.
[7]Gallmeier F X,Pevey R E.Creation of a Set of Interface Utilities to Allow Coupled Monte Carlo/Discrete Ordinate Shielding Analysis[C]//Third International Topical Meeting on Nuclear Applications of Accelerator Technology.USA:American Nuclear Society,1999:404-409.
[8]Gabriel T A et al.,CALOR:A Monte Carlo Program Package for the Design and Analysis of Calorimeter Systems,ORNL/TM-5619[R].USA:ORNL,1977.
[9]Cloth P,Filges D,Neef R D,et al.HERMES,A Monte Carlo Program System for Beam-materials interaction studies[R].Germany:KFA,1988.
[10]Urban W T,Seed T J,Dudziak D J.Nucleonic Analysis of a Preliminary Design for the ETF Neutral-beam-injector Duct Shielding[R].LA-UR-80-2926.New Mexico:Los Alamos Scientific Laboratory,1980.
[11]Chen Y.Coupled Monte Carlo-discrete Ordinates Computational Scheme for Three-dimensional Shielding Calculations of Large and Complex Nuclear Facilities[D].Germany:Forschungszentrum Karlsruhe,2005.
[12]Y.Chen, U.Fischer.Program System for Three-Dimensional Coupled Monte Carlo-deterministic Shielding Analysis with Application to the Accelerator-based IFMIF Neutron Source[J].Nuclear Instruments and Methods in Physics Research,2005,A(551):387-395.
[13]BRIESMEISTER J F.MCNP:A general Monte Carlo N-particle Transport Code,Version 4C,LA-13709-M[R].USA:Los Alamos National Laboratory,2000.
[14]RhoadesW A,Simpson D B.The TORT Three-Dimensional Discrete Ordinates Neutron/Photon Trans Port Code[R].ORNL/TM13221,Oak Ridge National Laboratory,1997.
[15]Carew J F,Hu K,Aroson A,et al.PWR and BWR Pressure Vessel Fluence Calculation Benchmark Problem and Solutions[R].Washington:Brookhaven National Laboratory,2001.
